




本节讨论二维数据的标准差、置信域和椭圆解析式的联系。如图2.12所示为9个线性相关性不同的随机数组。红色的椭圆描述了随机点的分布集中情况,会发现椭圆的大小、宽窄和旋转方向都有所不同。为了更好地描述这种联系,首先回顾一下椭圆这一基本概念。
如图2.13所示为经典椭圆形状,这个椭圆中心位于原点。 半长轴 (semi-major axis)位于 x 轴,长度为 a ; 半短轴 (semi-minor axis)位于 y 轴,长度为 b 。两个焦点位于 x 轴。这个椭圆的代数解析式为:

其中, a > b ,且 a 和 b 均大于0。下一步要研究这个椭圆绕原点旋转。
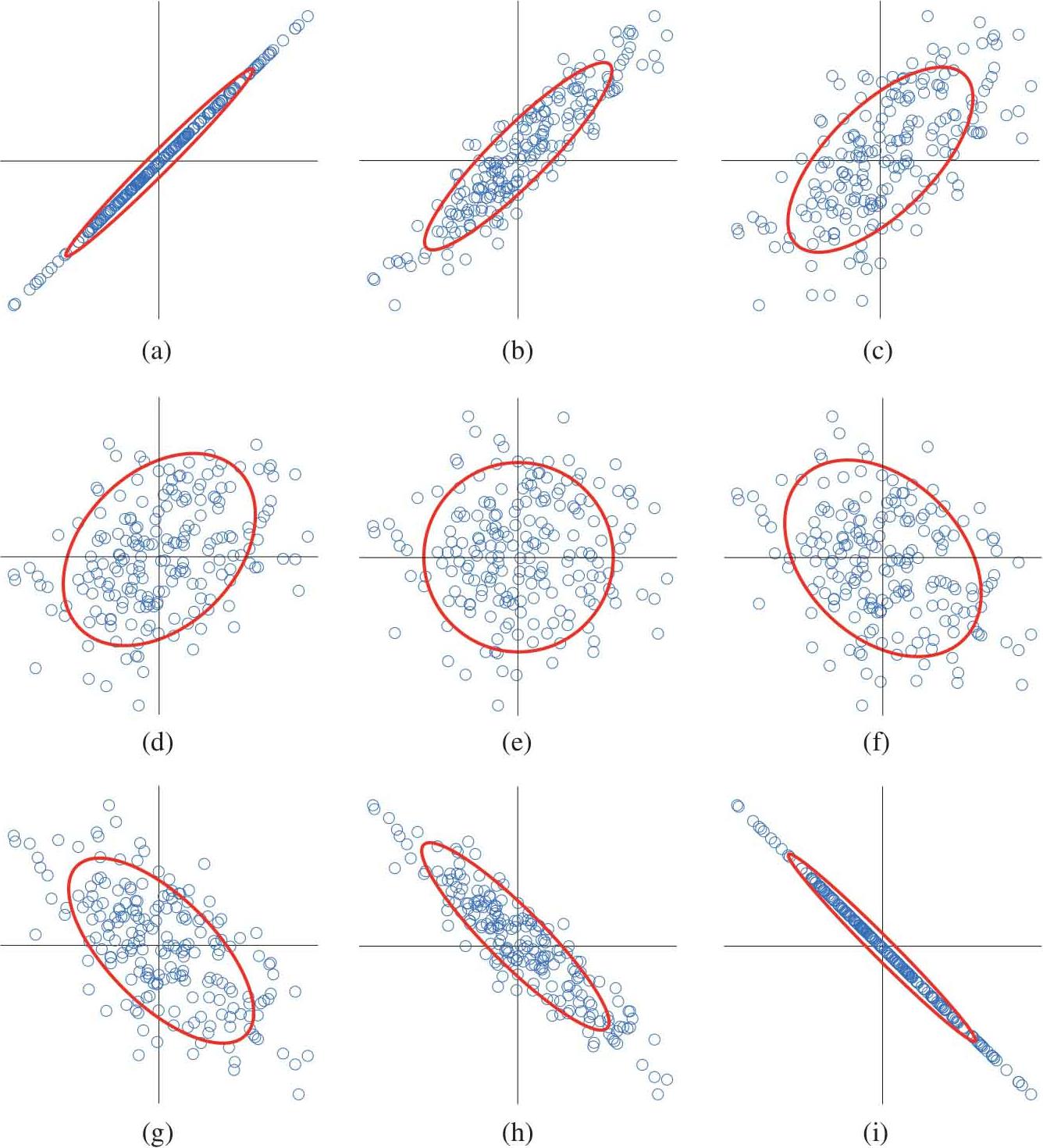
图2.12 二维平面旋转椭圆和随机数的关系
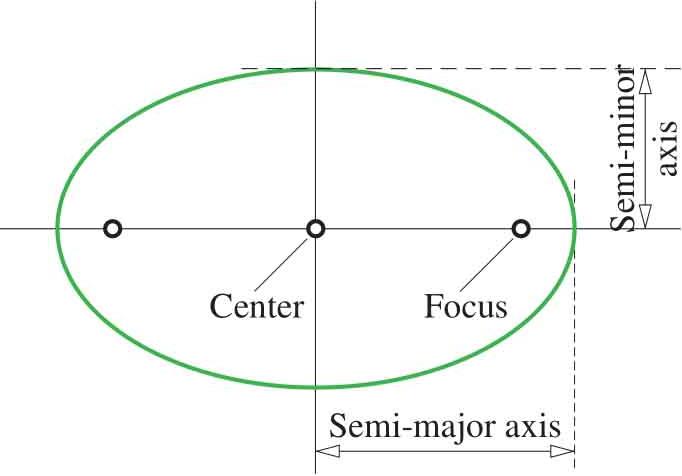
图2.13 经典椭圆形状
探讨随机数据处理时,第一步就是将数据中心化,因此这一节只讨论中心在原点的椭圆。中心在原点的椭圆一般形式可以写作:

椭圆上任意一点写作[ x 2 , y 2 ],式(2.32)可以用式(2.33)所示矩阵表达:
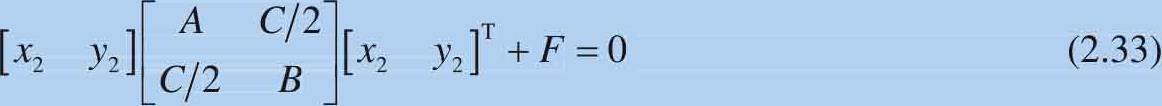
这个椭圆可以通过在原点的单位圆(半径为1)经过缩放、旋转和平移获得。第1章,已经探讨过如何用矩阵做缩放和旋转,下面就把它们应用在圆形向椭圆的转换上。单位圆的解析式为:

单位圆上的任意一点为[ x 0 , y 0 ], 单位圆 (unit circle)可用式(2.35)所示矩阵式来表达:
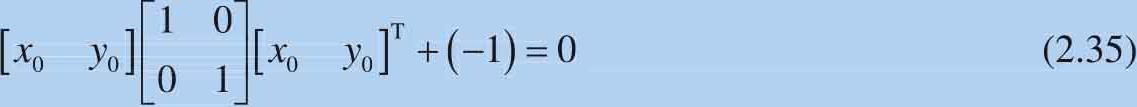
将 x 坐标扩大 a 倍,将 y 坐标值扩大 b 倍,获得[ x 1 , y 1 ],也就是:

求解[ x 0 , y 0 ],可以得到:
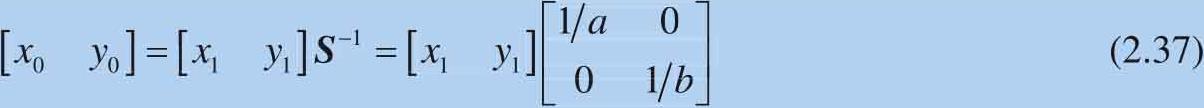
将式(2.37)代入单位圆矩阵式:
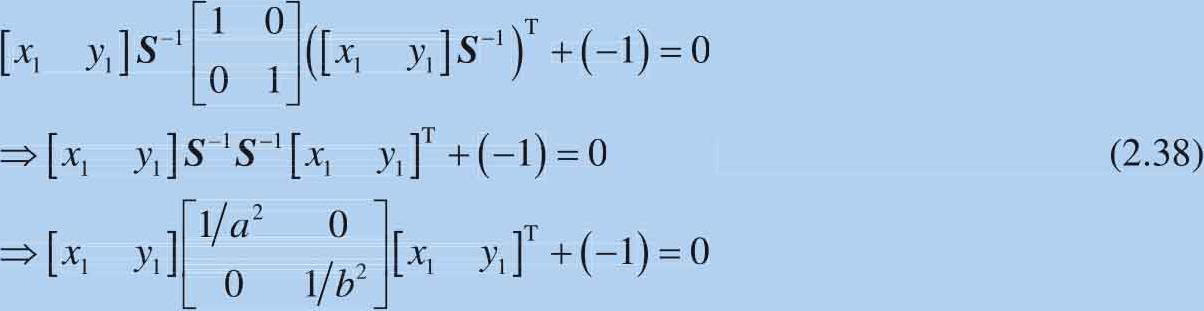
通过整理式(2.38),得到以原点为中心的椭圆:

式(2.39)两侧分别乘以 a 2 b 2 ,得:

再通过 R 矩阵对[ x 1 , y 1 ]进行旋转得到[ x 2 , y 2 ]:

即可建立[ x 0 , y 0 ]和[ x 2 , y 2 ]之间的联系:

将式(2.42)代入单位圆矩阵式:
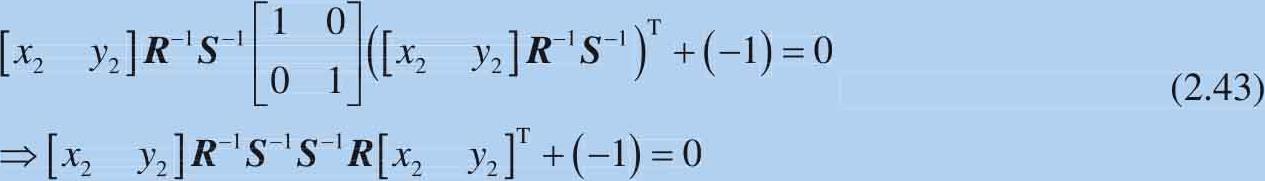
式(2.43)两侧同样乘以 a 2 b 2 ,有:
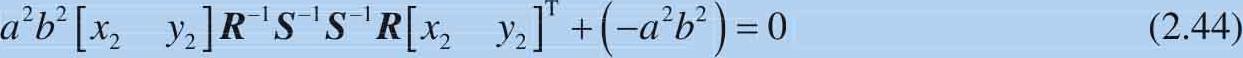
比较式(2.45):
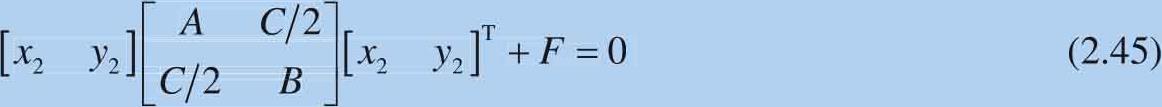
可以获得:

将 R 和 S 代入式(2.46)得:
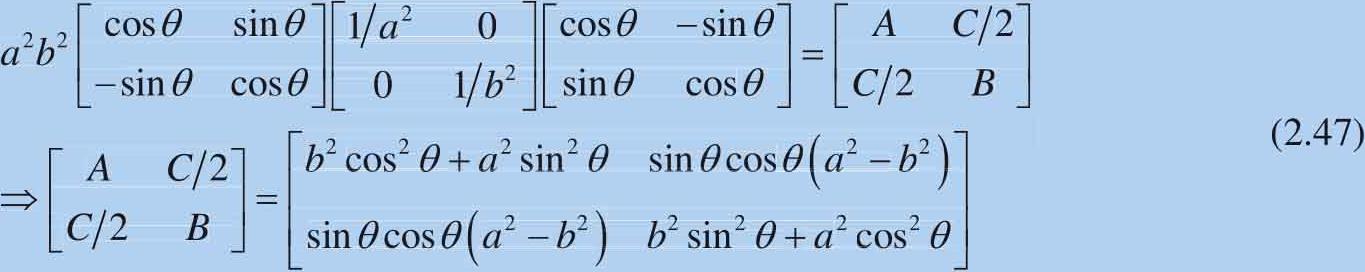
A 、 B 和 C 三个系数可以计算得到:

简单总结一下以上过程。首先构建单位圆的矩阵式,然后对单位圆进行缩放运算获得中心在原点的椭圆,然后将椭圆绕原点旋转。最后如果有必要,可以将椭圆整体平移到平面其他坐标点。如图2.14所示是这个椭圆变形的过程。丛书第四本还要从投影角度再次探讨这张图。
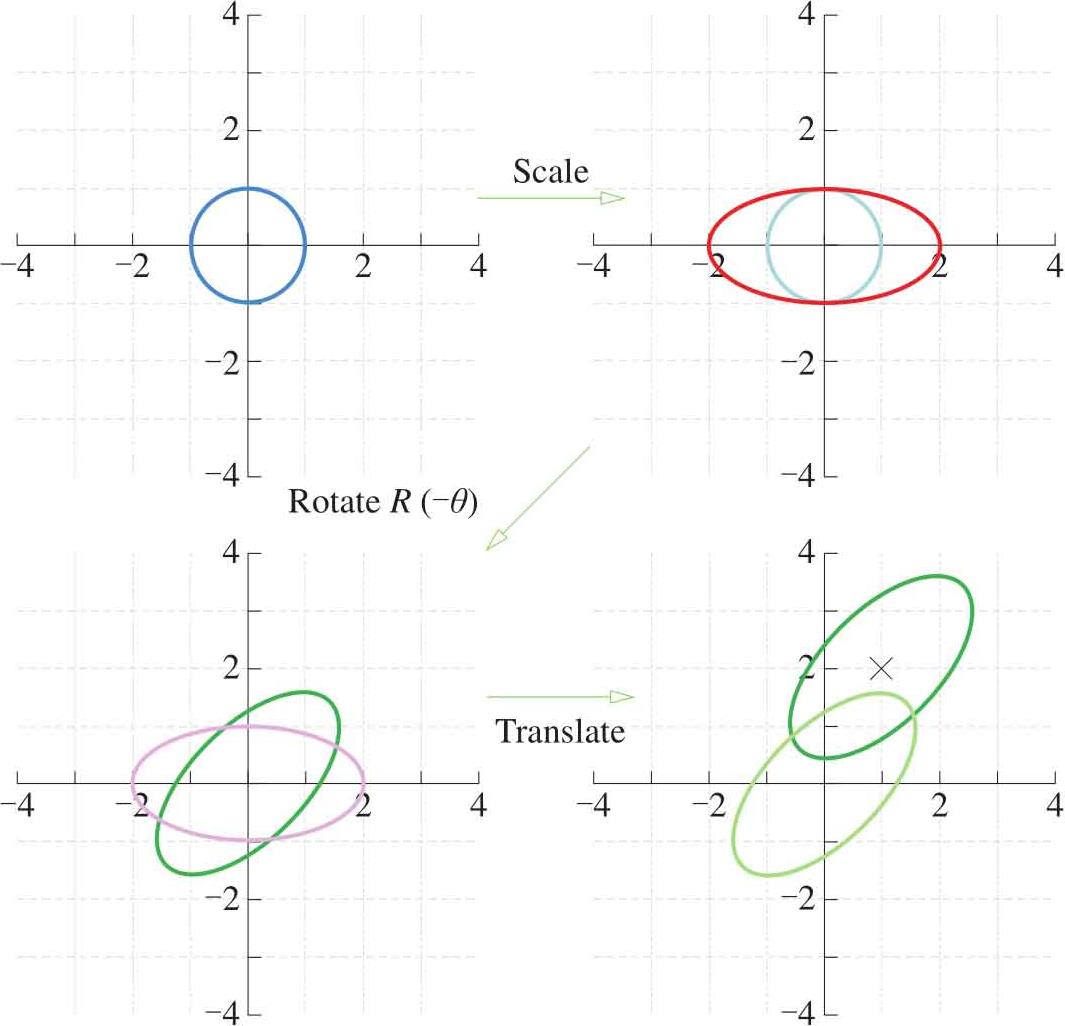
图2.14 椭圆的变形过程
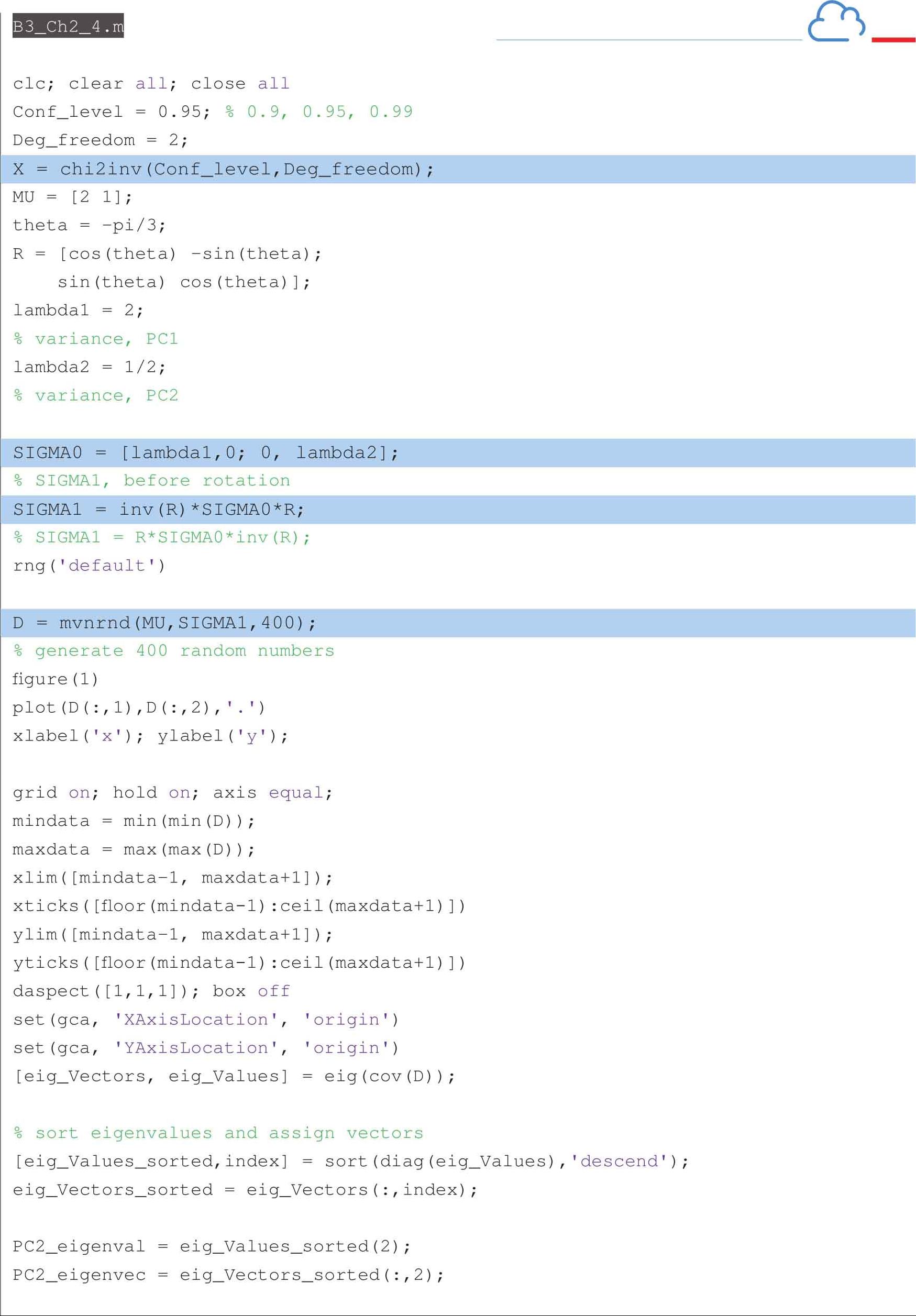
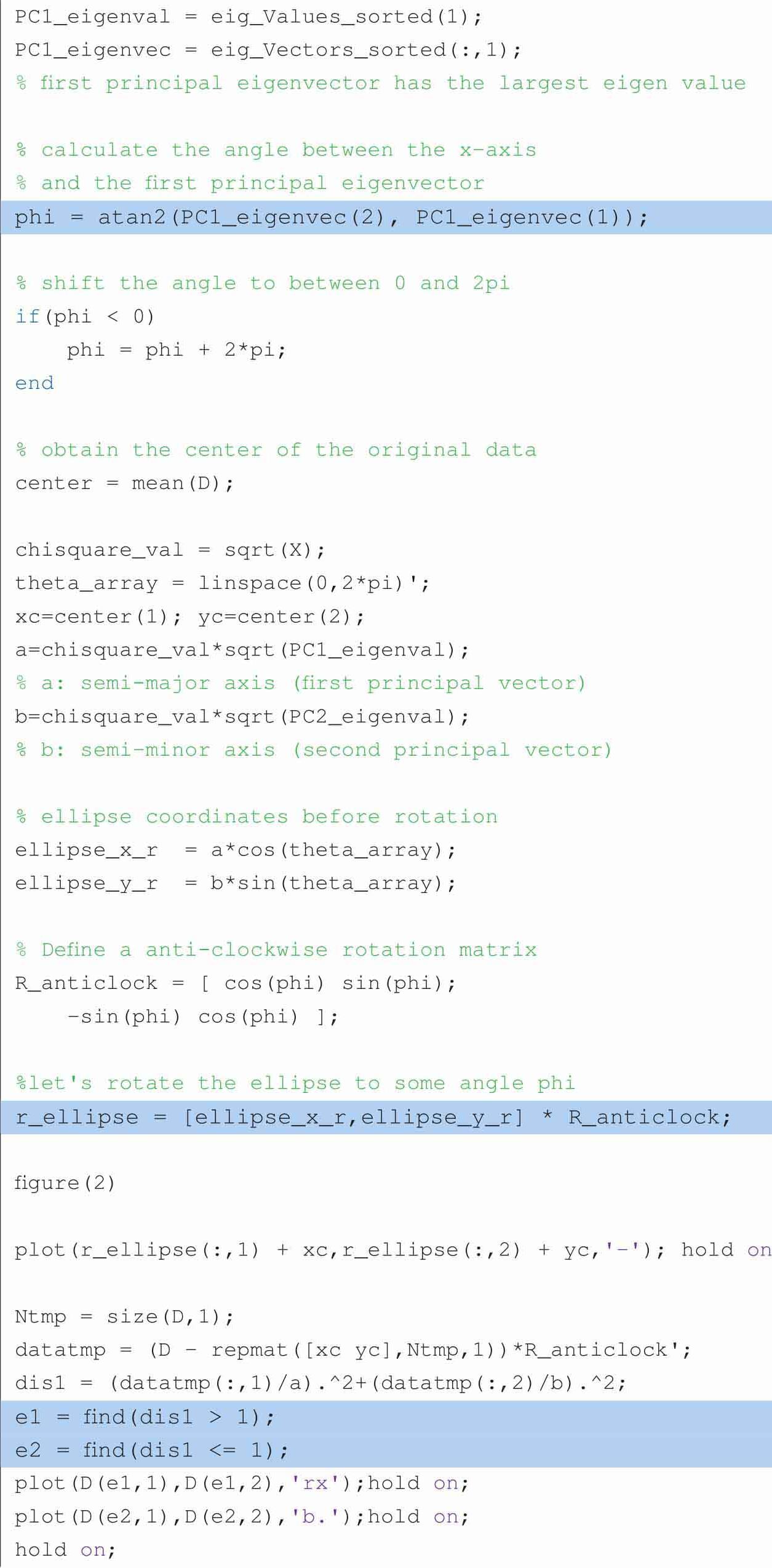
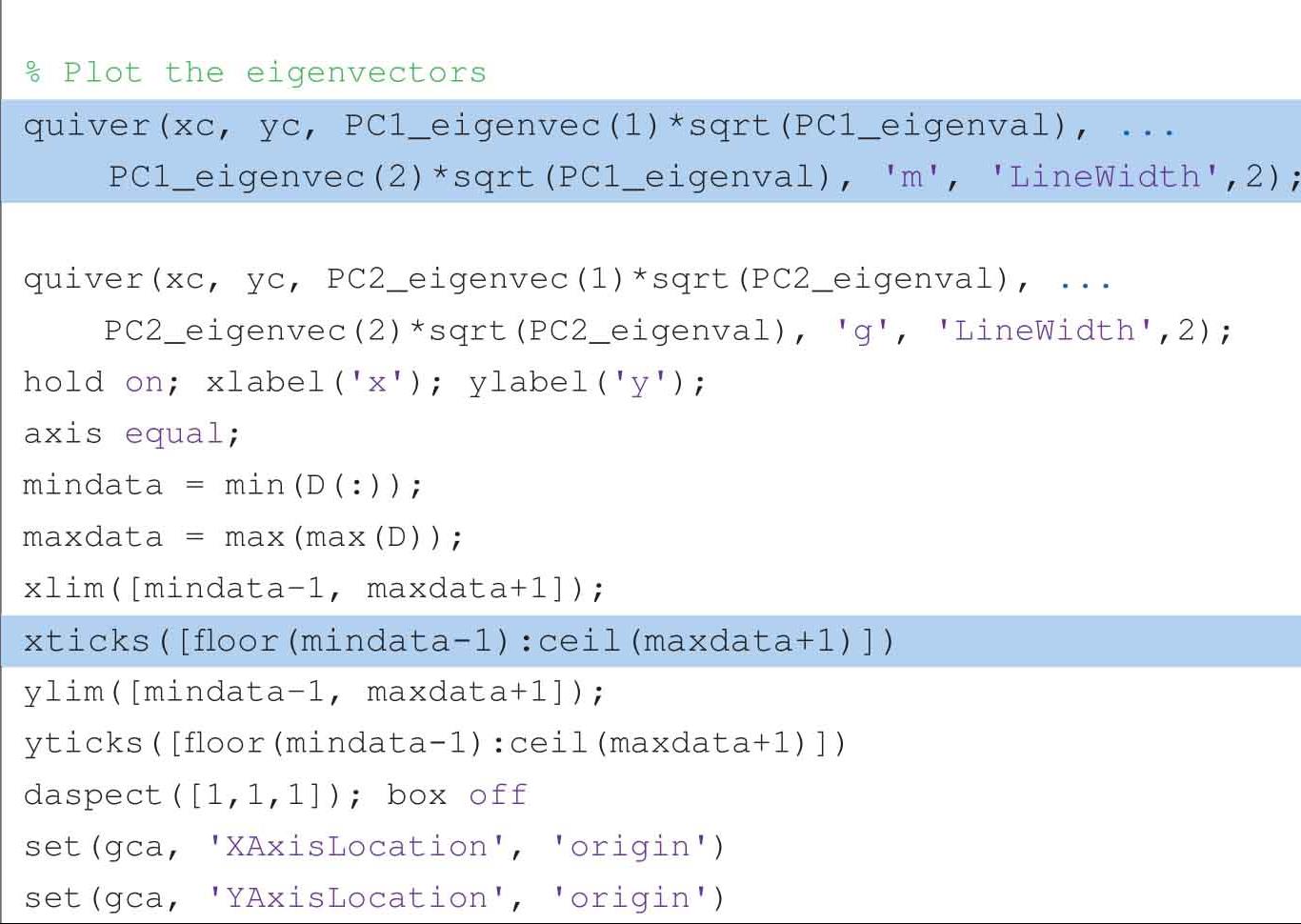
以下代码可以获得图2.14。
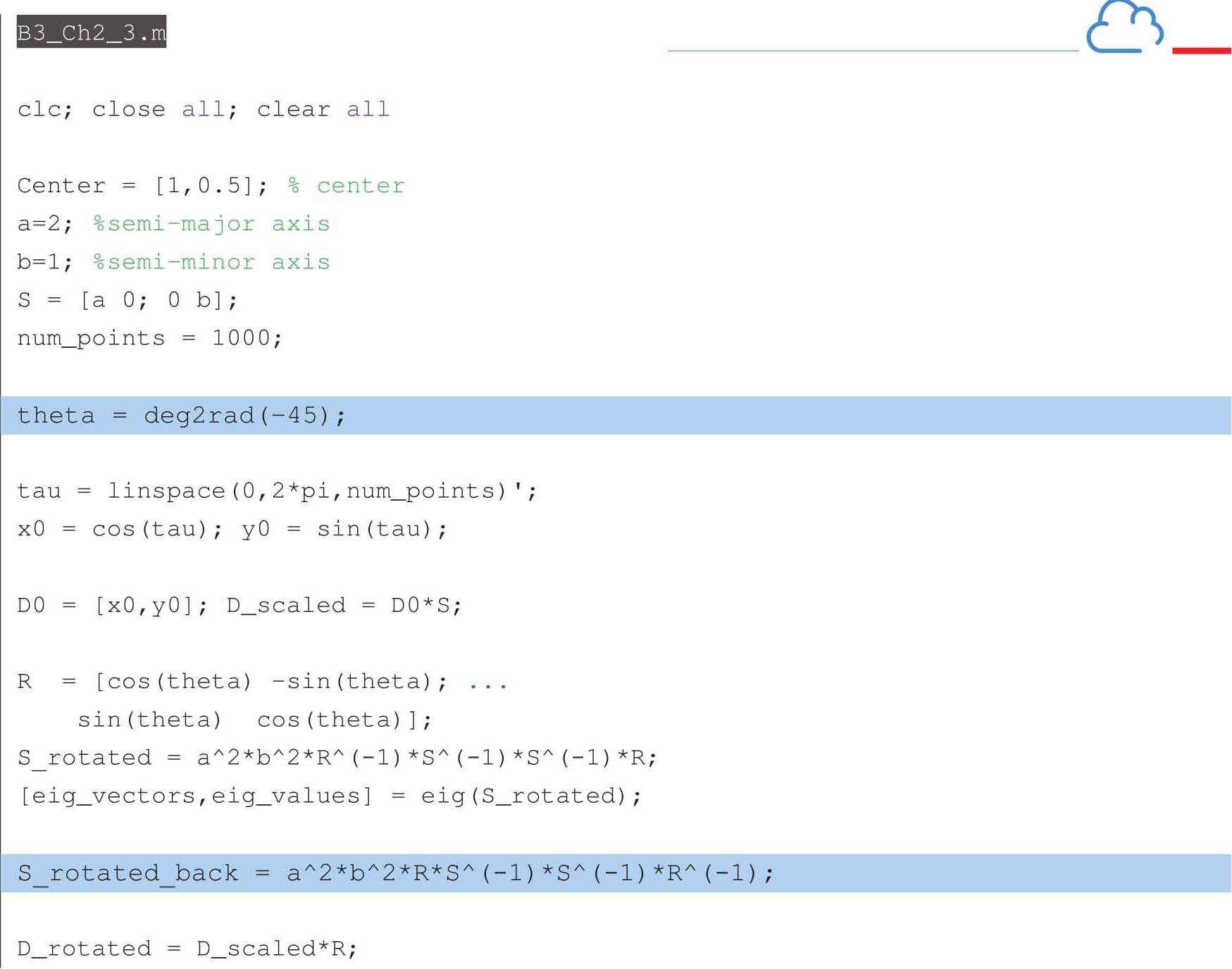


基于以上内容,现在讨论如何用数据的方差-协方差矩阵构建平面椭圆,从而表达数据集中度。如图2.15(a)(b)所示是同一组随机数。这组随机数在不同方向维度的数据分布情况完全不同。图2.15(a)给出的是在 x 和 y 轴两个方向的分布,会发现对于这组随机数 x 和 y 轴分布情况几乎一致。第1章计算过随机数的方差协方差矩阵,并且用eig()命令计算出其特征值和特征向量。对图2.15数据采用同样的分析方法,可以获得两个特征向量,将随机数据分别投影在这两个方向上,分别获得数据集中度最大和最小的分布范围。数据分布集中度大的方向对应的特征向量有最大的特征值,反之亦然。下一步,要构造的椭圆的半长轴就放置在数据分布集中度最大的方向上。椭圆的半短轴放置在数据分布集中度最小的方向上。在这两个方向上,可以计算出最大和最小的标准差,椭圆半长轴和半短轴的长度和这两个标准差呈正比例关系。
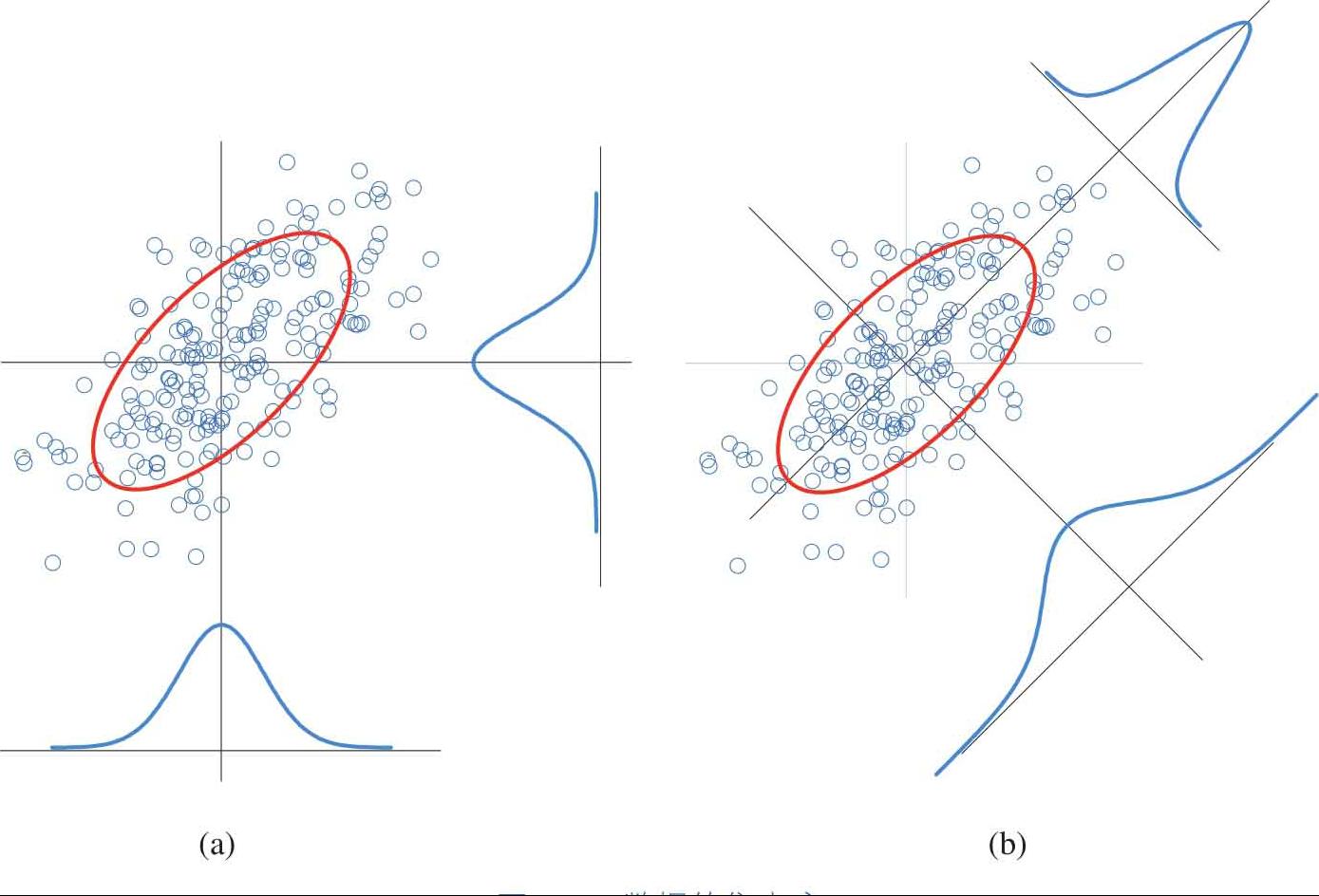
图2.15 数据的集中度
丛书第一本中统计部分讨论过一维数据的正态分布标准差和 置信区间 (confidence interval)这两者关系,如图2.16所示。本节把这个概念拓展到二维数据。第1章已经了解,二维数据 D ( L 行,2列)的方差-协方差矩阵 Σ 可以通过式(2.49)得到:

对 Σ 进行特征矩阵分解:

其中:
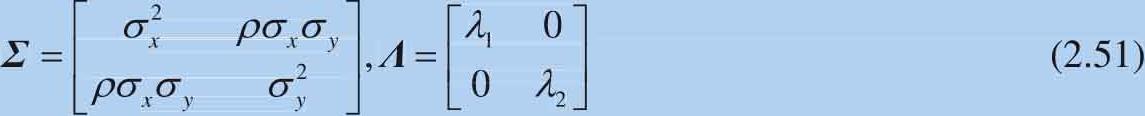
两个特征值对应的特征向量为:

这两个特征值可以通过式(2.53)求得:
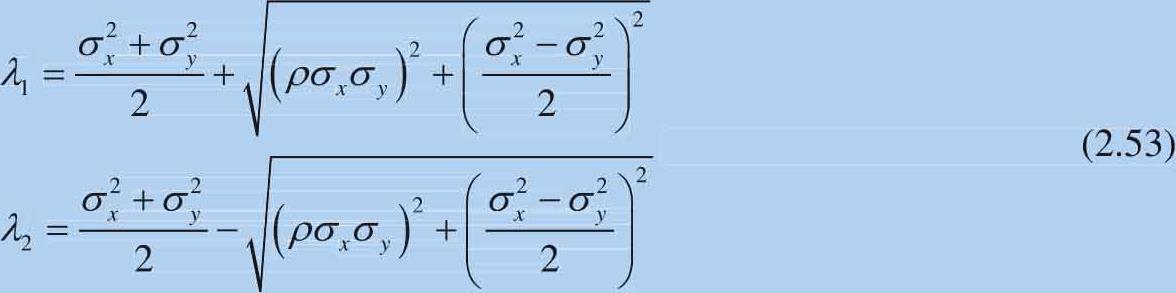
有兴趣的读者可以自行推导两个特征向量的解析解。在两个特征向量构建的新坐标系中,令特征向量 v 1 方向的坐标为 v ,特征向量 v 2 方向的坐标为 w 。数据在这两个方向的标准差为:

以下两个随机变量,线性无关且服从标准正态分布:
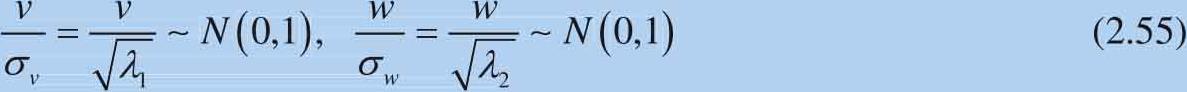
在 v - w 坐标系中,构造式(2.56)所示椭圆解析式:

这个椭圆的半长轴和半短轴的长度为:

特征向量 v 1 和 x 轴的夹角就是这个椭圆在 x-y 坐标系中,半长轴和 x 轴的夹角。这个椭圆在 x-y 坐标系中具体代数解析式本节前文已经分析过,这里不再赘述。这个椭圆的式(2.57)中的 ς 是在某个置信、某个具体自由度条件下的卡方分布值。例如,置信条件为0.95,自由度为2,卡方分布的值为5.9915,也就是说:

常见卡方分布值,请参考表2.1。
如图2.17所示是一组随机数,如图2.18中所示的椭圆是图2.17随机数95%置信区间。“·”代表在95%置信区间内的数据;“×”代表95%置信区间之外的数据。
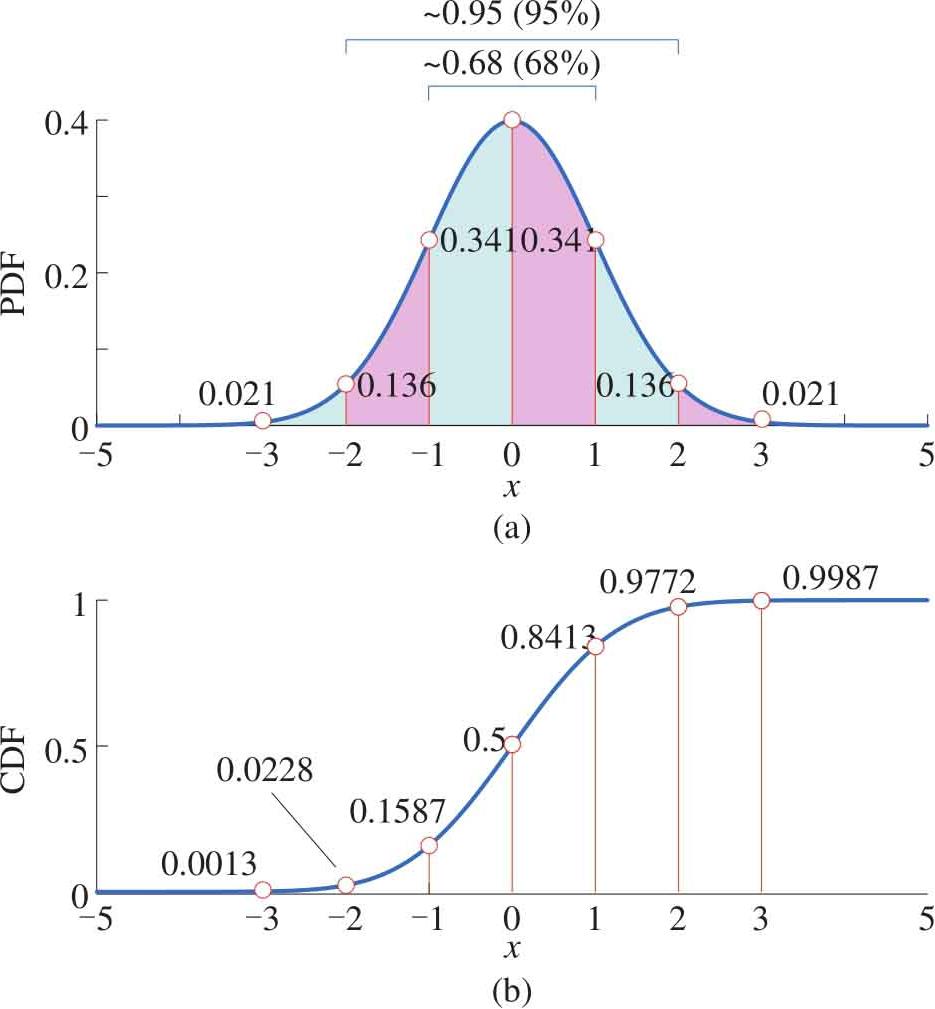
图2.16 标准正态分布标准差间距的区间内概率值
表2.1 常见卡方分布值
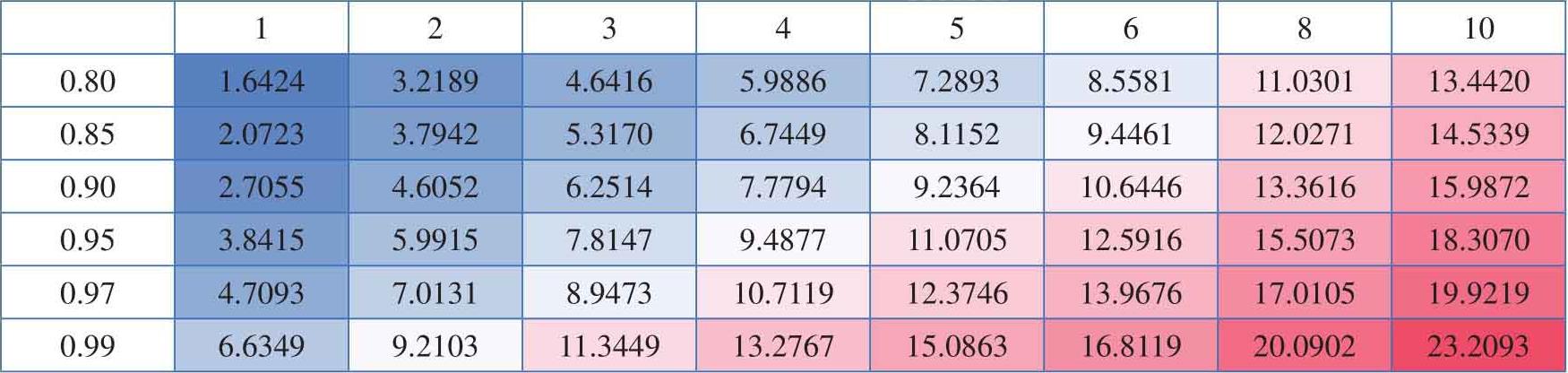
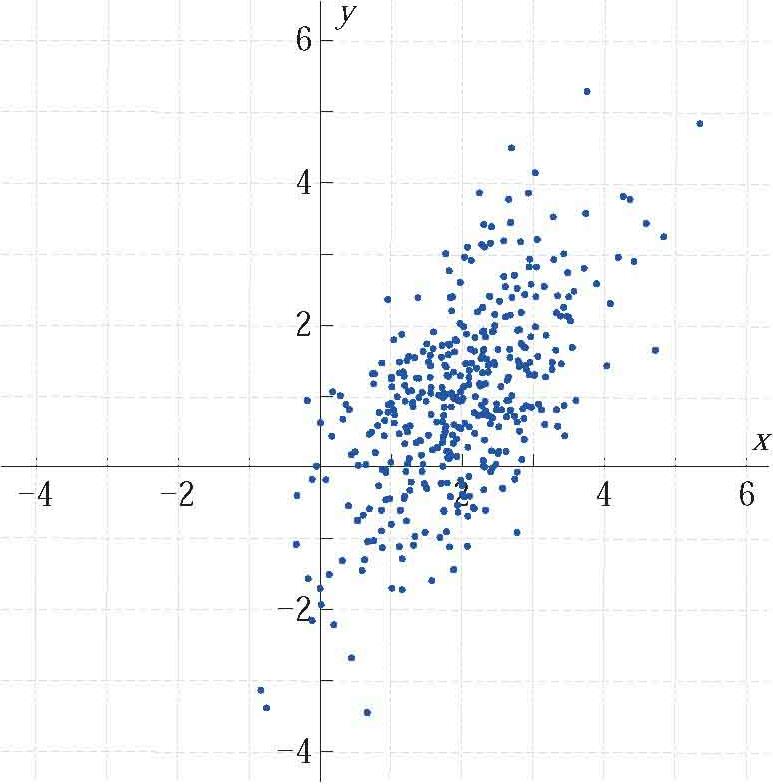
图2.17 二维随机数据
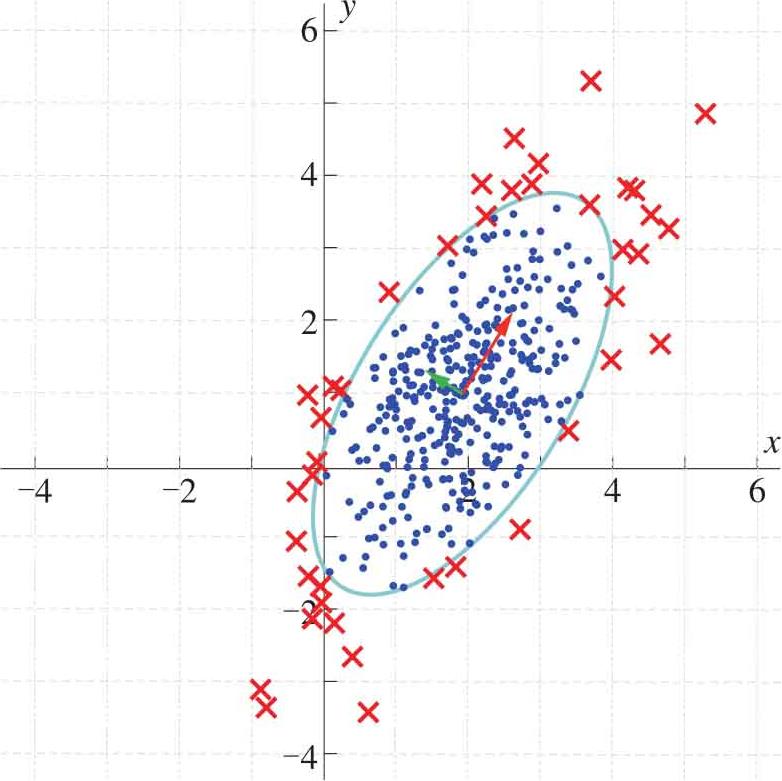
图2.18 二维随机数据95%置信区域
以下代码可以绘制并比较90%和99%置信区域。
多元正态分布 (multivariate normal distribution)的概率密度函数为:
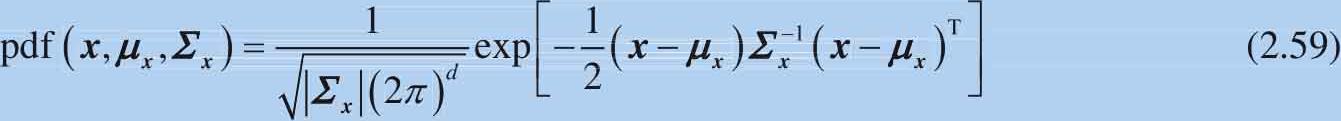
式中: x 和 μ x 为1× d 形状的行向量; Σ 为形状 d × d 的方差-协方差矩阵。 d 为多元正态分布维度。
当 d =2时, x 和 μ x 可以表达为:

如果 x 1 和 x 2 之间的相关性为0,方差-协方差矩阵可以写作:

二元正态分布的概率密度函数可以写作:
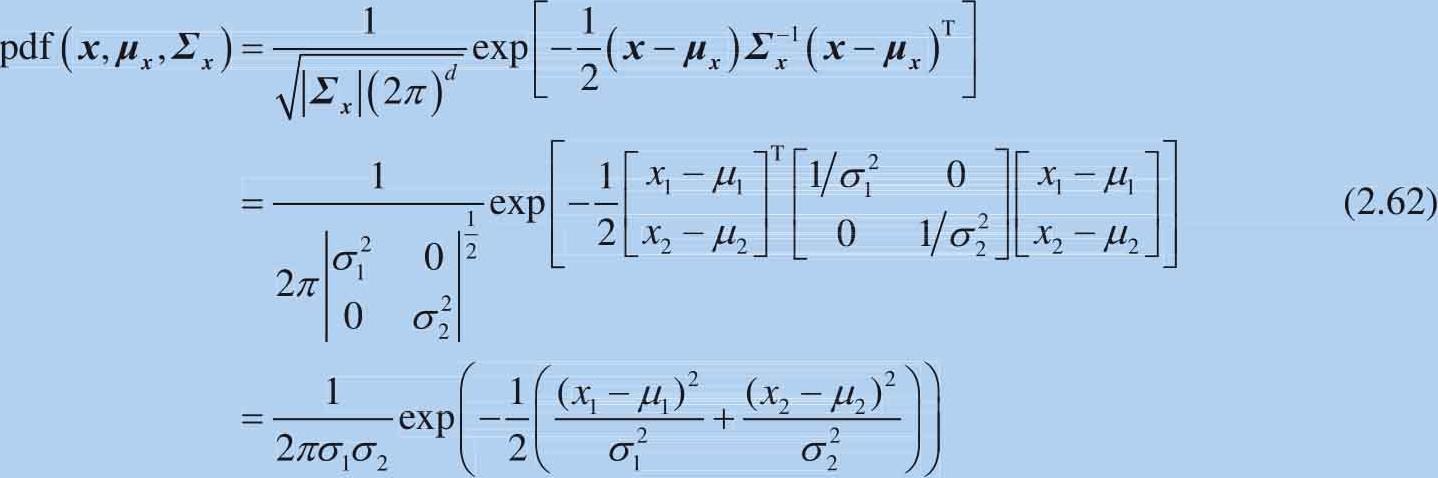
假设概率密度函数等于某个值 c ,即:
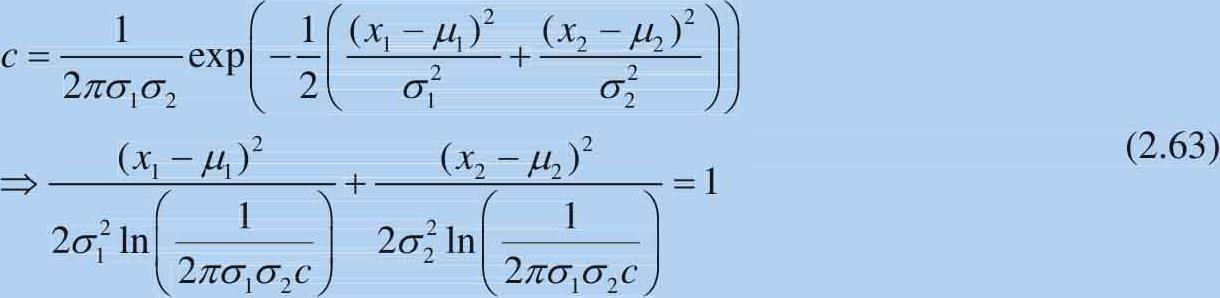
从式(2.63)可以看到一个圆心位于( μ 1 , μ 2 )的椭圆。如果相关系数不为0,方差-协方差矩阵可以写作:

这种条件下,二元正态分布的概率密度函数为:
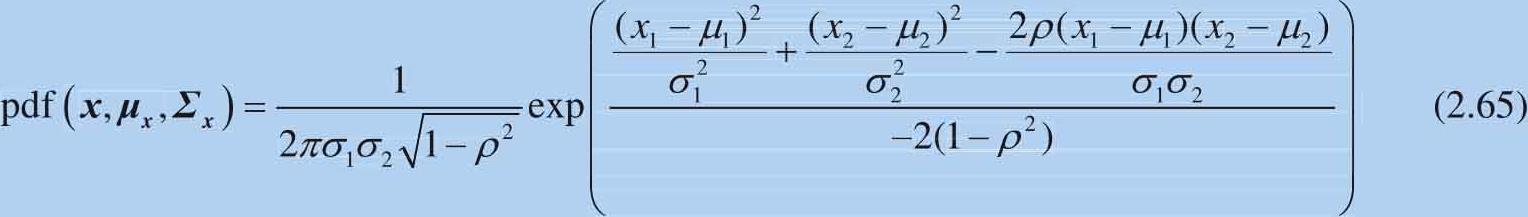
类似地,当概率密度为另一个定值时,就可以得到一个旋转椭圆。丛书第四本会继续探讨椭圆和其他圆锥曲线的性质。