




本节要利用 指数加权 (exponentially weighted)计算平均值、方差-协方差矩阵和相关性矩阵等。指数加权这个方法,在金融风险管理计算波动率和计算VaR已经讨论过,这里用矩阵式展示计算过程。在指数加权条件下,首先定义权重列向量 w EW :

第 i 个权重 w EW _ i 可以表达为:

权重列向量 w EW 元素的和为1:

另外当 T 较大时,比如 T =252, λ T 可以看作为0,因此第 i 个权重 w EW_ i 可以表达为:

在不同衰减因子 λ 条件下, w EW 随系数 i 变化如图1.42(a)所示。注意,时间的先后顺序是从左到右,右侧 i =1为窗口内最新数据。
第1到第 m 个权重之和,可以通过式(1.99)求得:

如图1.42(b)所示为从右向左求cumsum()结果的图像。图中给出在不同 λ 条件下,求和结果分别为0.9和0.95的情况。另外, m 可以求解出来,如式(1.100)所示:

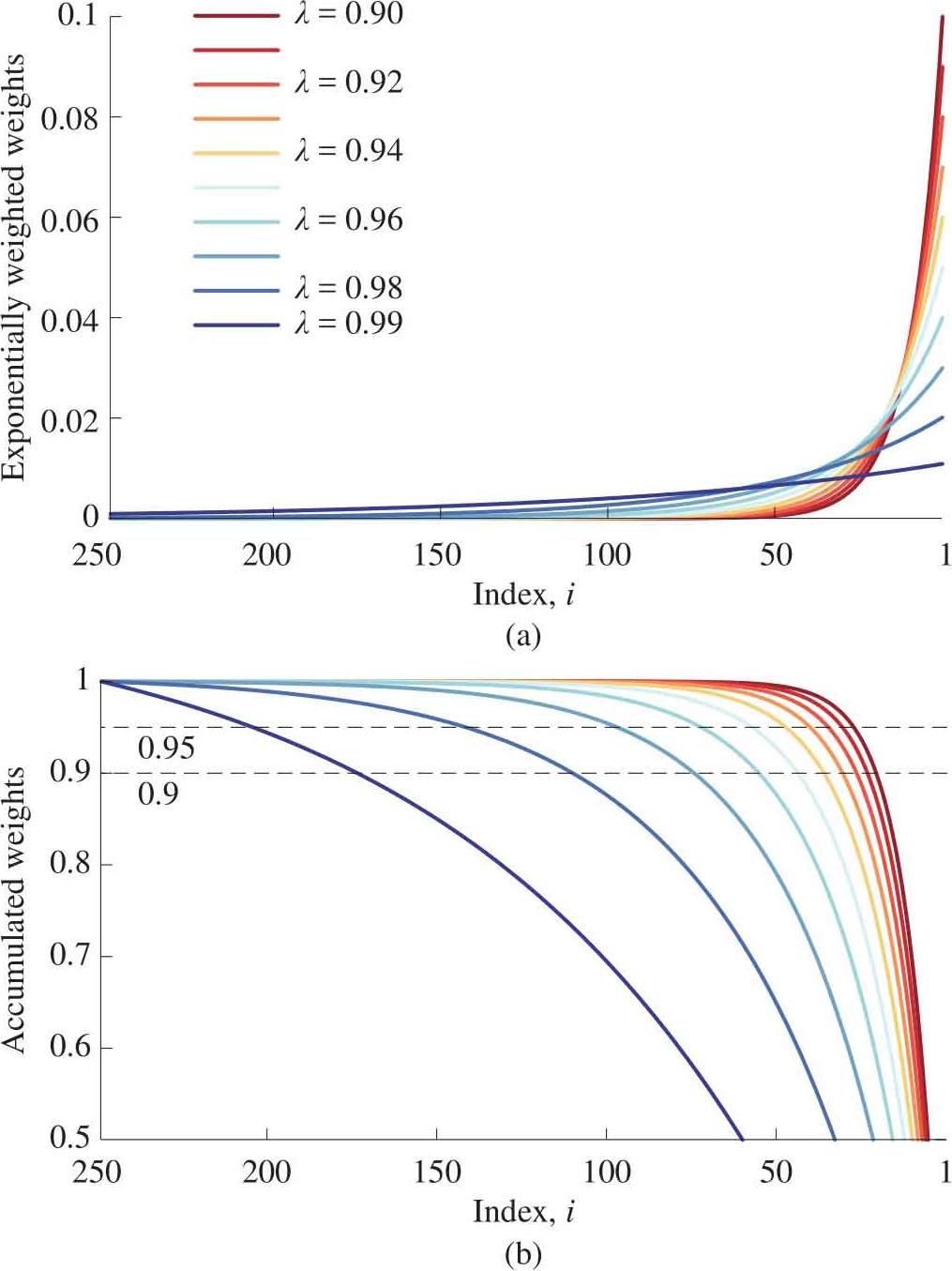
图1.42 w EW 随系数 i 和 λ 变化
同样认为 λ L 为0,式(1.100)可以写作:

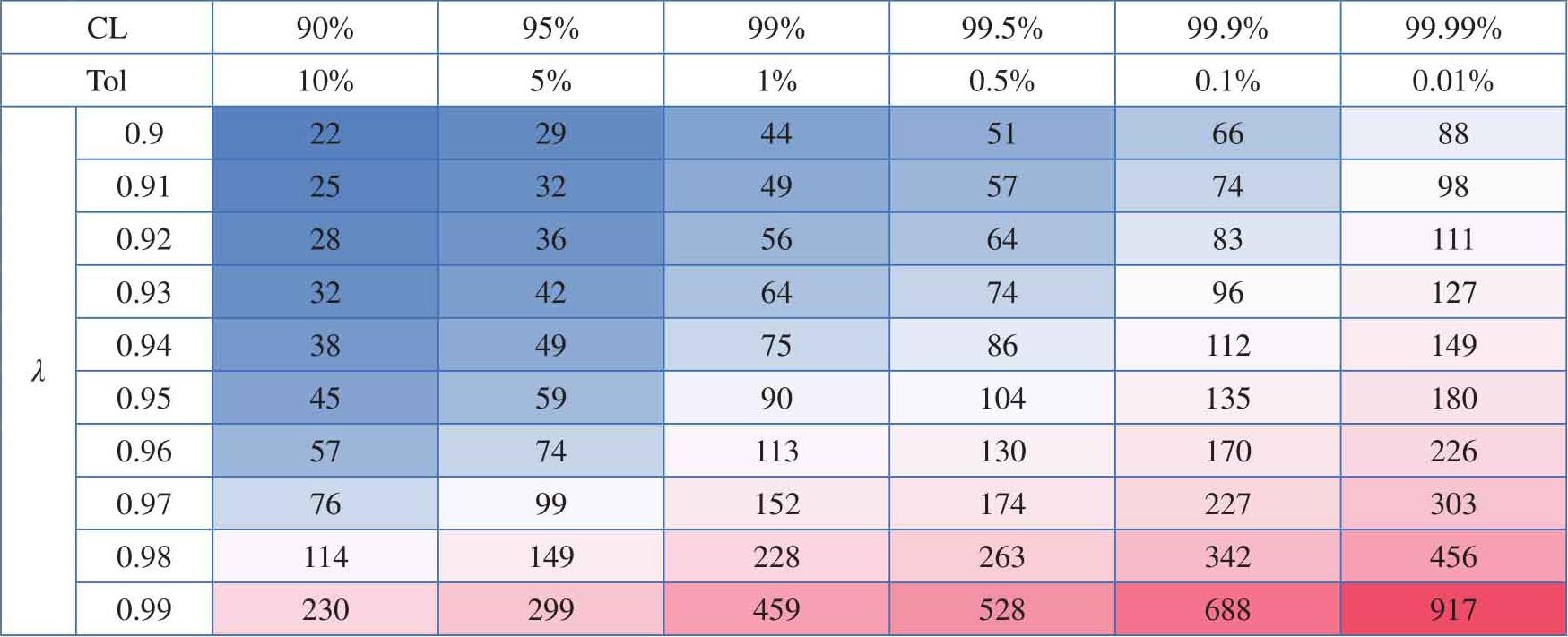
式(1.101)中tol为 容差 (tolerance)。表1.1给出的是,在不同 λ 条件下,权重和CL分别为90%、95%、99%、99.5%、99.9%和99.99%时, m 的值。
表1.1 不同 λ 和CL条件下历史数据的数量
下面定义一个向量 λ :

λ 和 w EW 的关系如下:

如图1.43所示, D 在列方向的 指数加权平均数 (exponentially weighted average)为:

指数加权平均方法配合移动窗口方法,就得到前文讲过的指数加权移动平均方法。
现在把EWA计算平均数这个思路运用在求解方差-协方差矩阵。类似地,计算去均值时,原数据减去的是EWA:

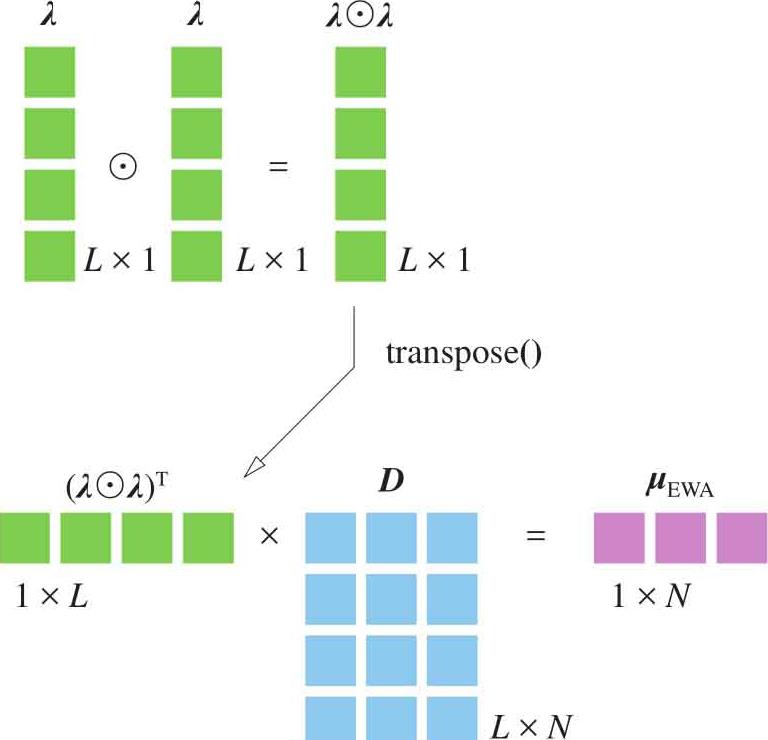
图1.43 矩阵表达加权平均数
另外,如果均值近似于0,可以不去均值。为了便于计算,先定义一个矩阵 R EWMA :

如图1.44所示是 R EWMA 计算过程。
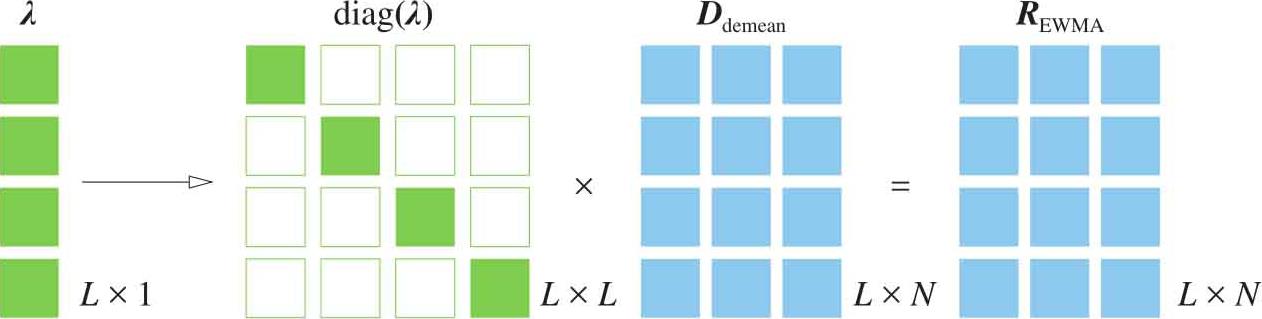
图1.44 矩阵表达计算 R EWMA
如图1.45所示,EWMA方差-协方差矩阵可以通过式(1.107)计算出来:
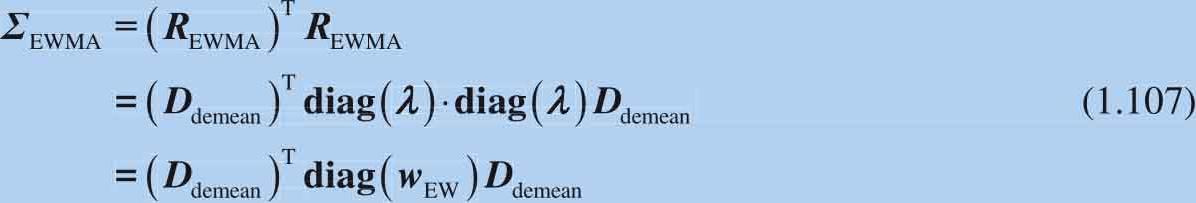
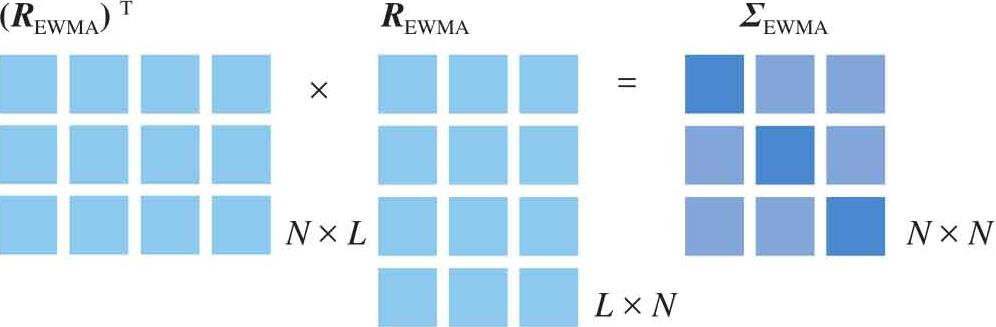
图1.45 EWMA方差-协方差矩阵
如图1.46所示,方差列向量可以通过式(1.108)计算得到:

方差对角矩阵通过式(1.109)获得:

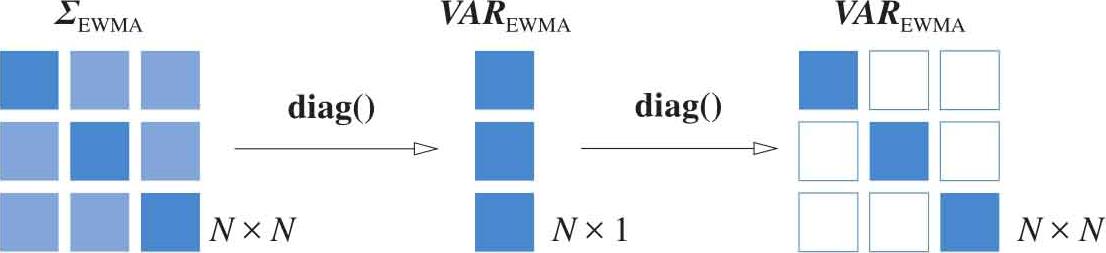
图1.46 EWMA方差
现在下载四只股票数据,用250数据长度作为窗口,用几种方法计算方差-协方差矩阵。如图1.47所示就是这四个计算结果。图1.47(a)展示的是用最常用的统计方法计算方差-协方差矩阵。图1.47(b)展示用EWMA方法计算方差-协方差矩阵,但是没有对于 D 采用去均值化。这种方法被广泛采用,因为很多统计分布的均值接近0,因此对原始数据通常不需要做任何去均值化处理。图1.47(c)也是用EWMA方法,但是对原始数据去均值化,均值是用简单方法获得。图1.47(d)也是用EWMA方法,去均值化采用EWA。
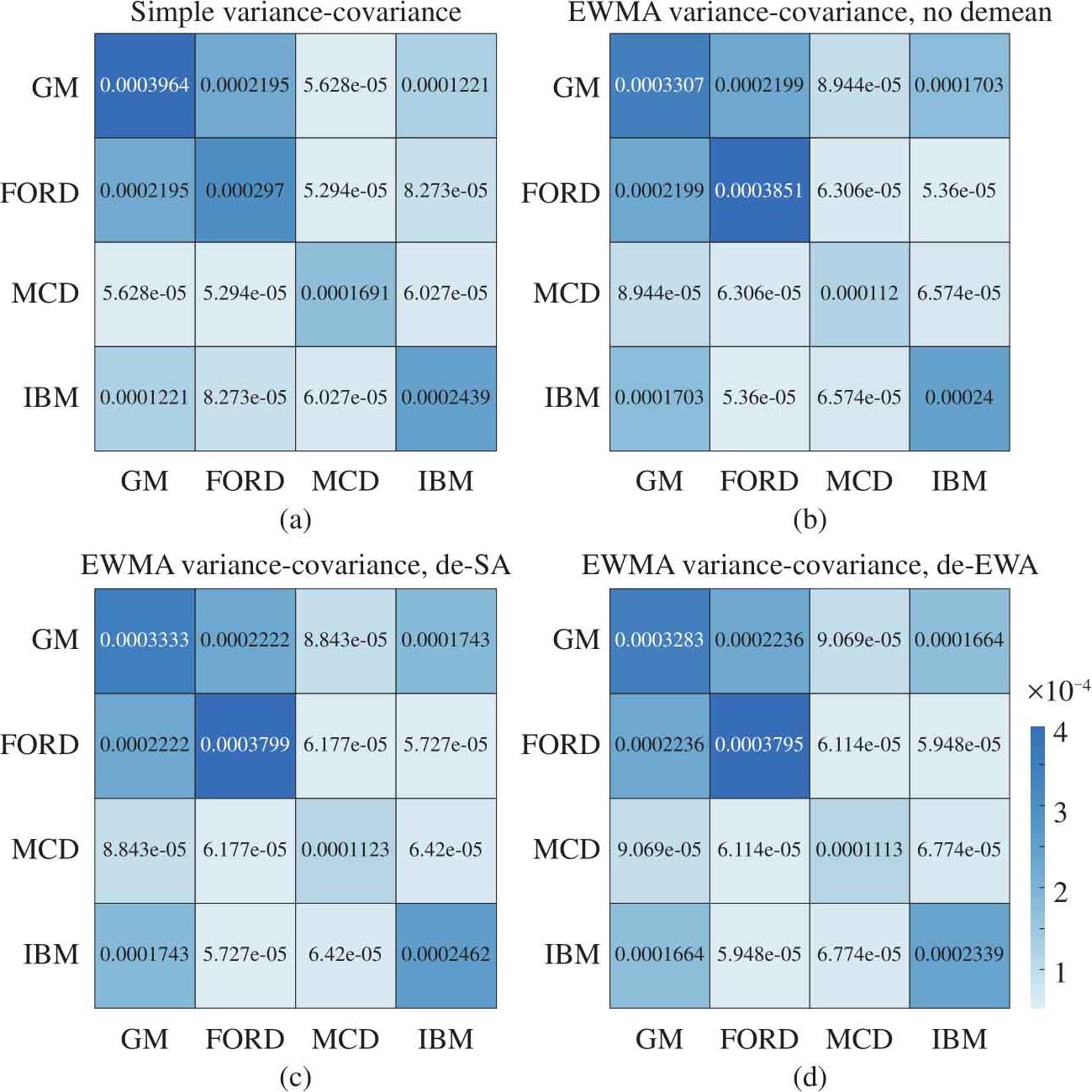
图1.47 股票数据用四种方法计算方差-协方差矩阵
如图1.48所示,EWMA标准差通过式(1.110)获得:

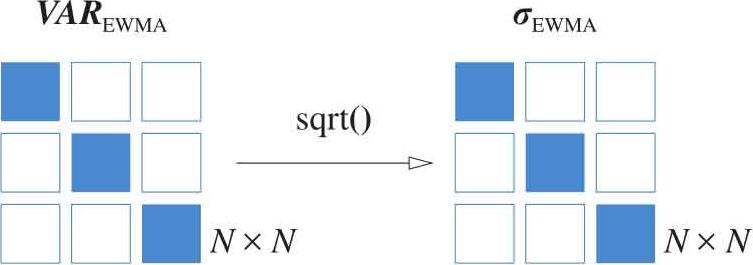
图1.48 EWMA标准差
相关性矩阵可以通过式(1.111)求得:

图1.49所示是股票数据用四种方法计算相关性矩阵。
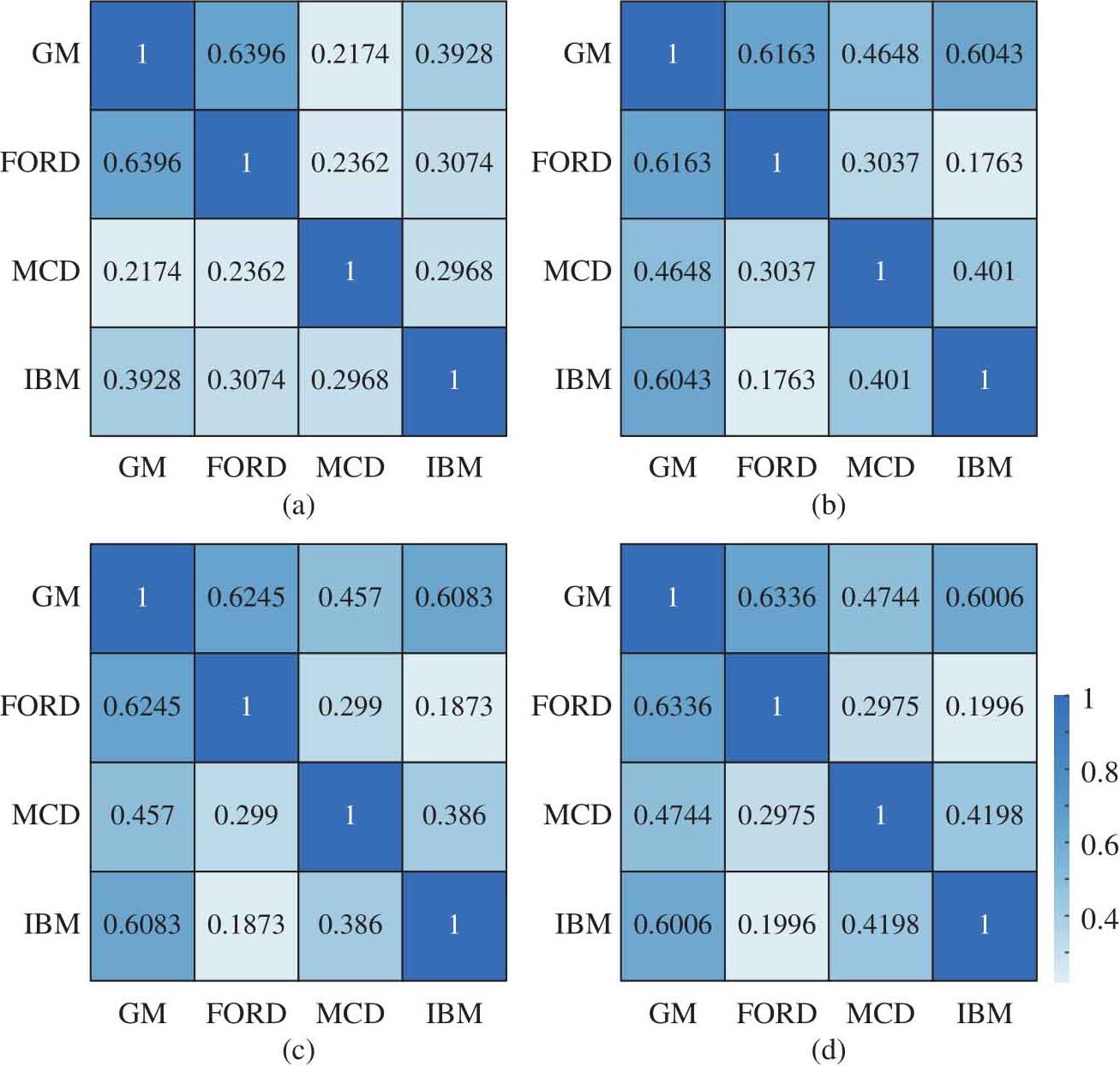
图1.49 股票数据用四种方法计算相关性矩阵
以下代码可绘制图1.47和图1.49:

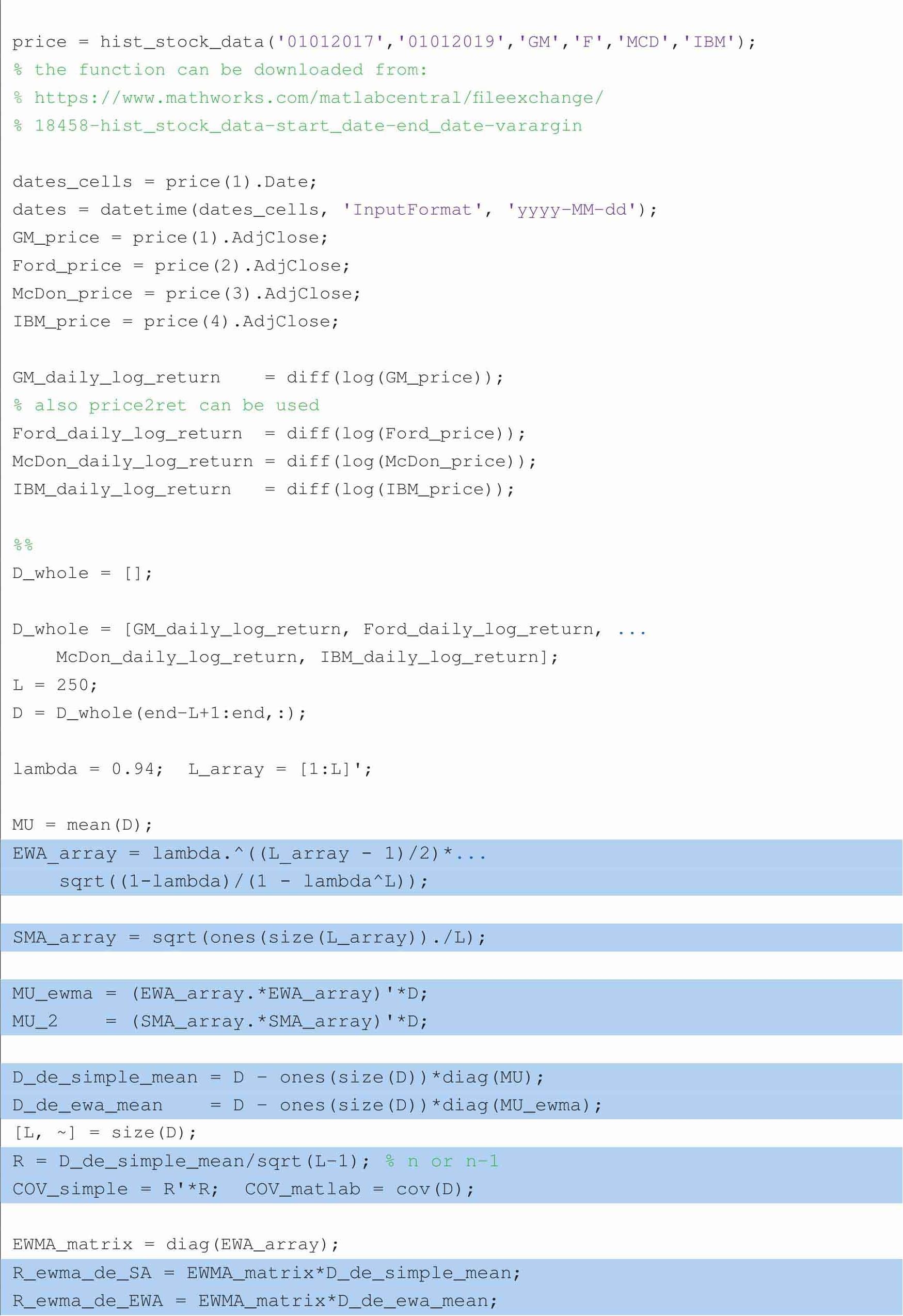


本章主要讨论了矩阵的基础运算、矩阵转化、矩阵分解、线性方程组等矩阵基础内容;另外,特别介绍了矩阵与概率运算的关系。第2章将进一步探讨矩阵和其他数学运算的融合。这两章内容会为以后复杂的金融建模打下坚实数学基础。