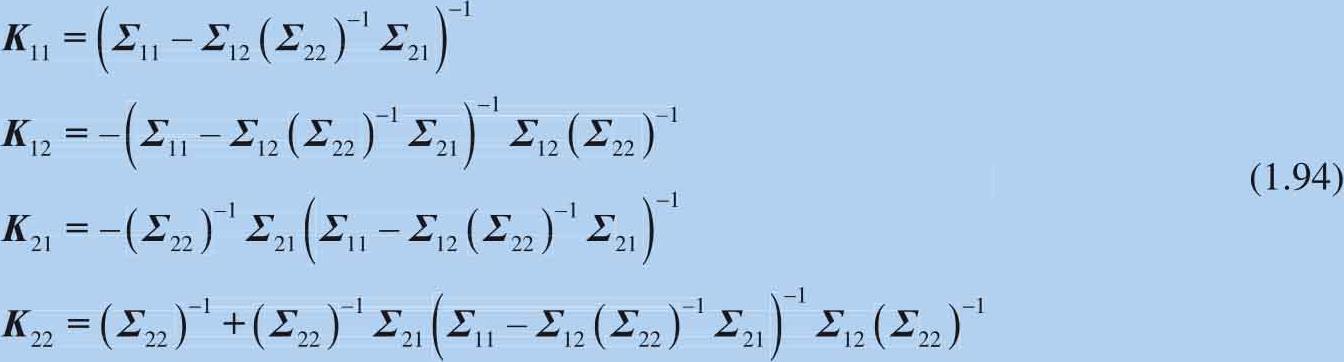本节及下一节将介绍矩阵在概率计算中的应用。首先,用矩阵式来计算平均数。对于形状为 L × N 矩阵 D ,如图1.31所示,含有 N 列的观测数据,比如 N =3,可假设是三只股票的对数回报率序列。 L 是每个数据序列的长度,比如 L =252,即252个日观测值。 D 可以表示为:

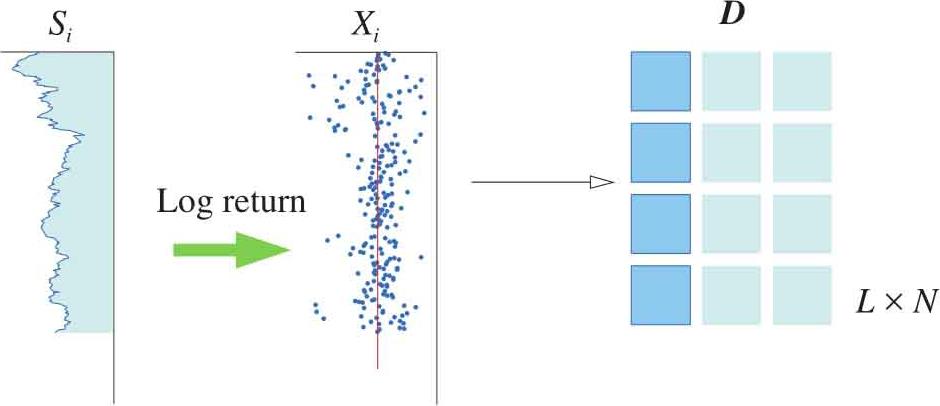
图1.31 矩阵 D 结构
下面定义一个权重列向量 w ,形状为 L ×1:

如图1.32所示, D 在列方向的 简单平均数 (simple average, SA)可以通过式(1.80)计算出来:

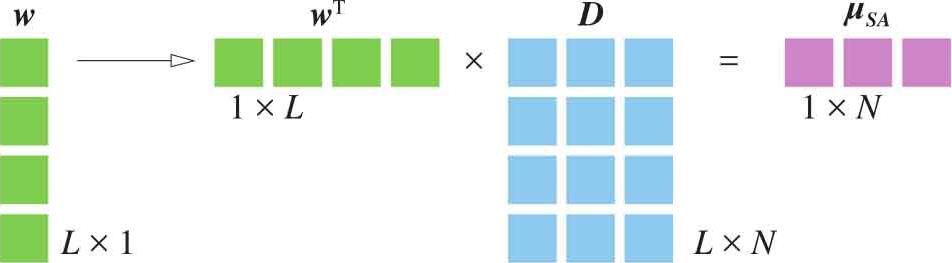
图1.32 矩阵表达平均数计算
去均值 D demean 的计算过程可以用图1.33表达。去均值 D demean 可以减去简单平均数:
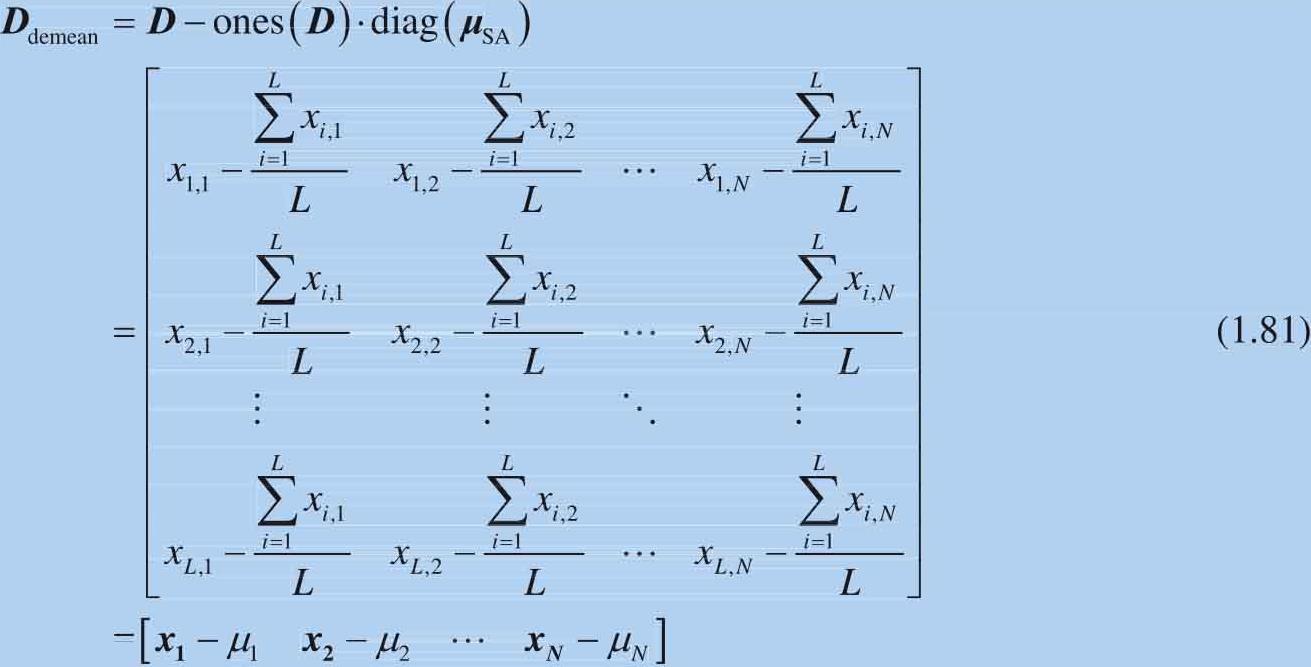
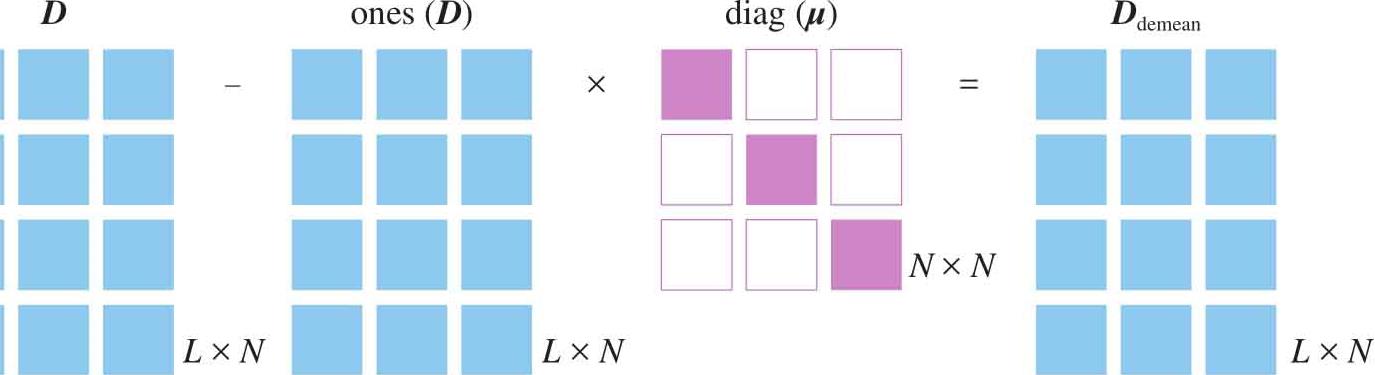
图1.33 矩阵表达去均值
以下三种方法,可以实现去均值的目的:
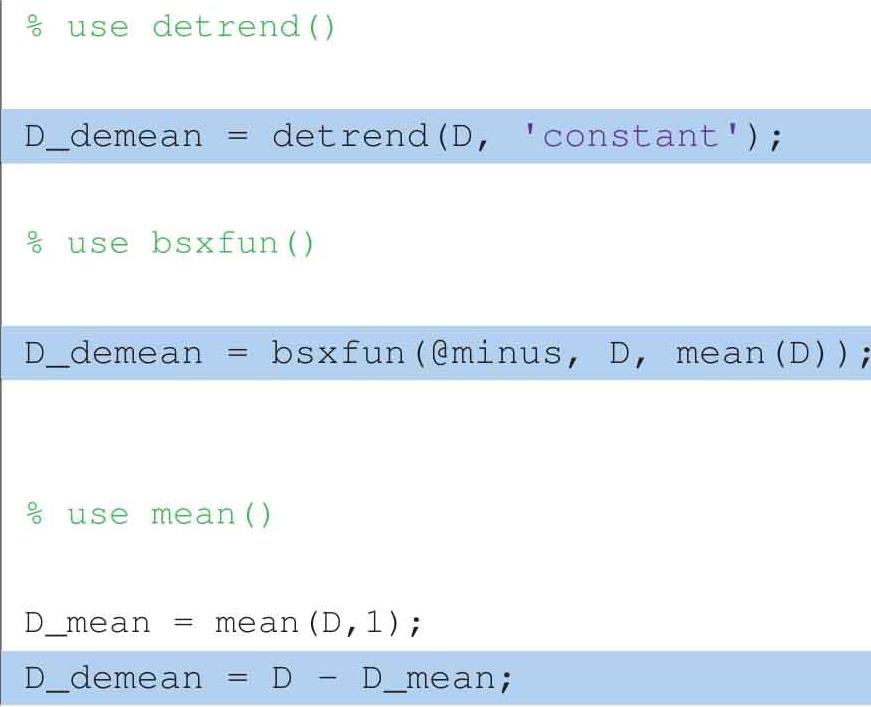
detrend()这个函数会在本书数据部分做进一步的介绍。
利用 D demean 可以求解样本 方差-协方差矩阵 (variance-covariance matrix):

计算总体方差-协方差矩阵时,分母为 L 。图1.34展示方差-协方差矩阵计算过程;注意,图1.34展示矩阵运算,没有考虑分母项标量。
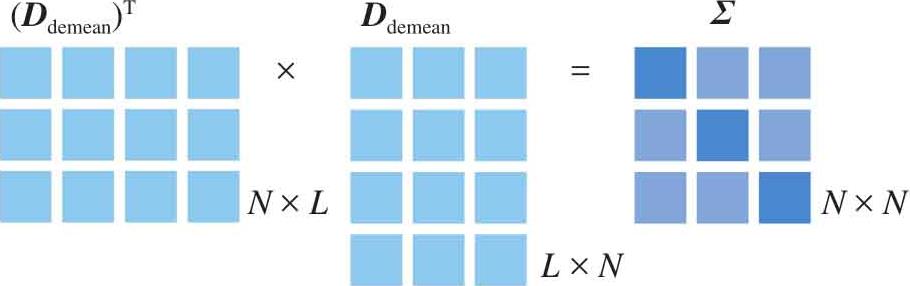
图1.34 方差-协方差矩阵
方差-协方差矩阵第( j , k )元素:
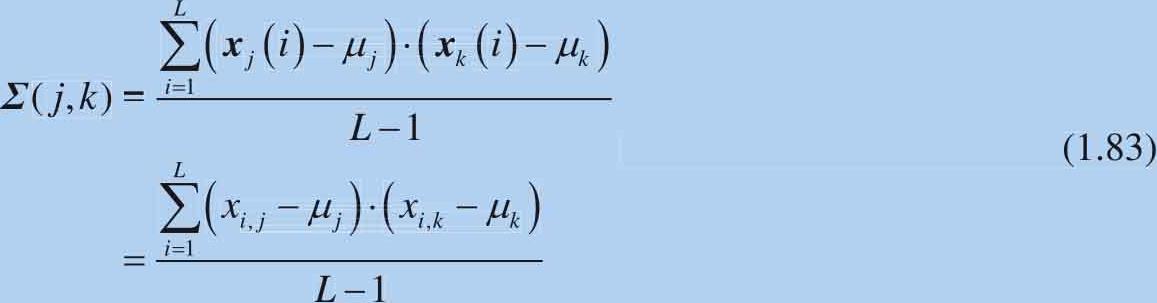
比较方差协方差矩阵计算结果如图1.35所示。

图1.35 比较方差-协方差矩阵计算结果
方差-协方差矩阵中的第 k 个对角线元素( k , k )是第 k 列数据的方差:
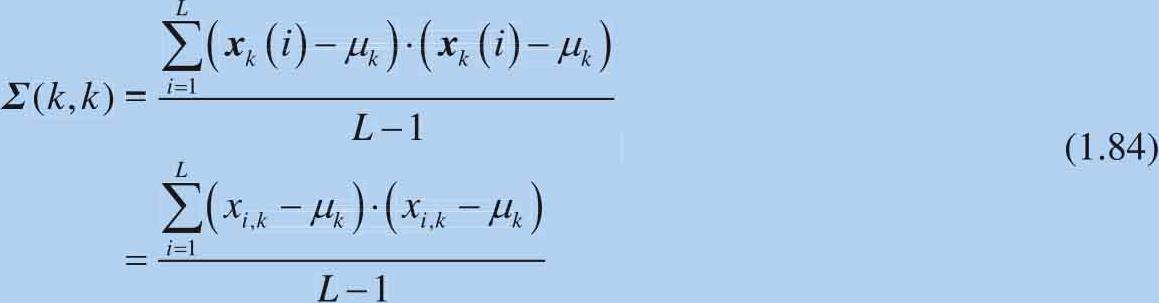
如图1.36所示, VAR 为方阵,对角线元素一一对应 Σ 对角线元素,即方差。
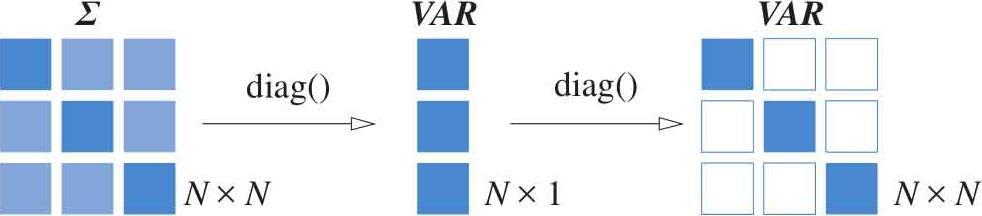
图1.36 方差
如图1.37所示,标准差通过式(1.85)计算获得:

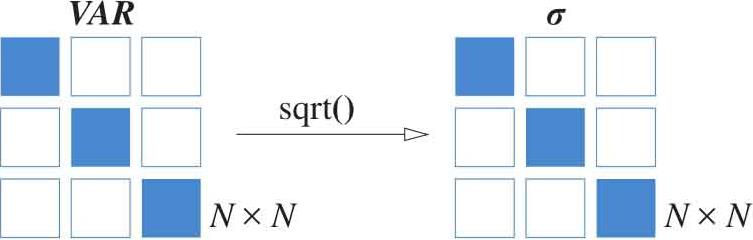
图1.37 标准差计算
相关性矩阵 (correlation matrix)如图1.38所示,可以通过式(1.86)求得:


图1.38 相关性计算
比较相关性矩阵计算结果如图1.39所示。

图1.39 比较相关性矩阵计算结果
以下代码可绘制图1.35和图1.39:

分块矩阵 (block matrix)是将大块矩阵分割成较小的矩阵,这样可以简化运算,同时也会让运算过程变得更加清晰。
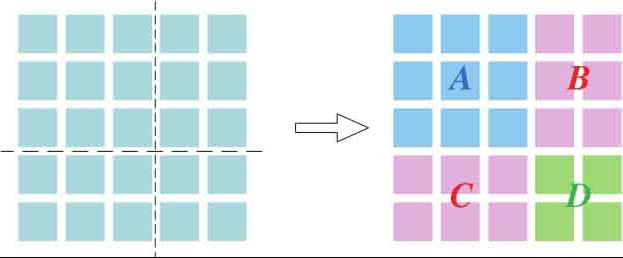
图1.40 分块矩阵
下面介绍一种本书后文会用到的分块矩阵运算。如图1.40所示,一个方阵可以分割成若干个较小的矩阵 A 、 B 、 C 和 D ,其中 A 和 D 为方阵。这个分块矩阵的逆可以表达为:
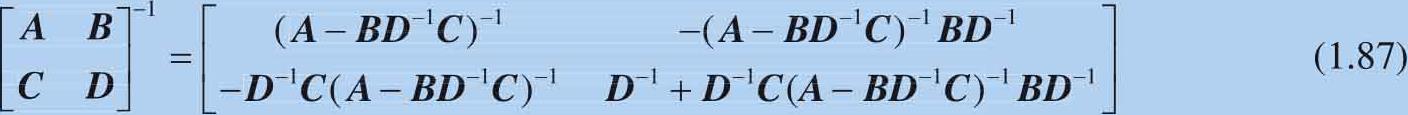
令:

分块矩阵的逆可以写作:

这个分块矩阵的逆还可以表达为:
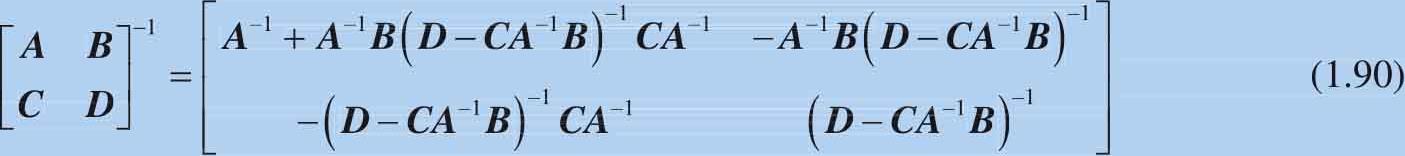
令:

分块矩阵的逆可以写作:
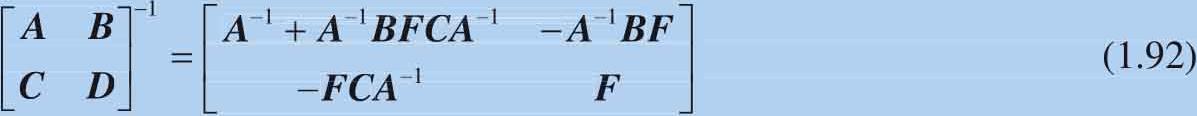
下面把分块矩阵求逆思想应用在方差-协方差矩阵上。如图1.41所示是一个方差-协方差矩阵 Σ 被分为四块: Σ 11 、 Σ 12 、 Σ 21 和 Σ 22 。
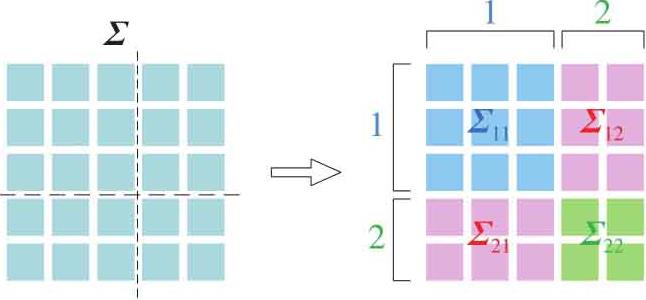
图1.41 方差-协方差矩阵分块
Σ 11 和 Σ 22 都是对称矩阵,而且主对角线元素为方差。 Σ 12 和 Σ 21 这两个分块矩阵中没有方差,只有协方差。 Σ 12 的转置矩阵为 Σ 21 。 Σ 的分块矩阵逆可以记作:

其中: