下载掌阅APP，畅读海量书库
立即打开
线性方程组 （system of linear equations, linear system）指的是各个方程关于未知量均为一次的方程组。下面以二元一次方程组和三元一次方程组，来简单介绍一些线性方程组的特点。式（1.71）给出的是 m 个线性方程：
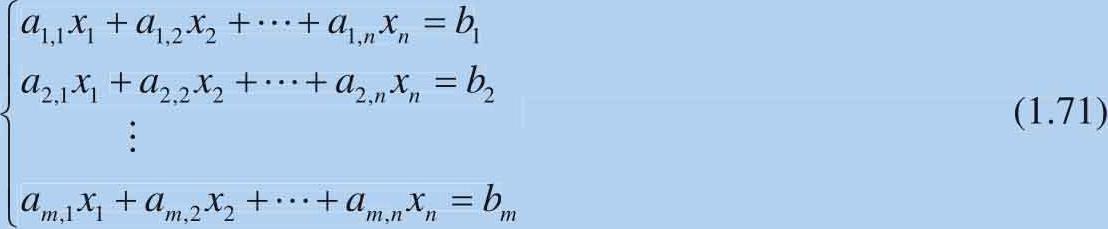
其中 x 1 、 x 2 到 x n 为 n 个未知数， b 1 、 b 2 到 b m 为 m 个常数项， a m ， n 为未知数系数。以矩阵形式可以得到式（1.72）：
其中：
如果存在一组数 x 1 、 x 2 到 x n 使得线性方程等式成立，那么这组数就叫作方程组的解。假设矩阵 A 为方阵，且可逆，采用矩阵表达线性方程组求解：
矩阵 A 的逆影响线性方程组解的情况。线性方程组解的情况有三种： 唯一解 （single unique solution）， 无解 （no solution）和 无穷多组解 （infinitely many solutions）。下面从几何角度来解释这三种情况。
丛书第一本曾提及过，二元一次方程在几何上是平面的一条直线，三元一次方程是空间的一个平面。如图1.30（a）所示的是二元一次线性方程组有唯一解的情况，图1.30（a）中可以看到两条直线有唯一交点。图中的两条直线的线性方程组可以表达为式（1.75）：
以下三组MATLAB代码可以用来求解式（1.75），并且比较运算时间：
如图1.30（b）所示的是二元一次线性方程组无解的情况，两条直线平行。线性方程组可以表达为：
其中，对应矩阵 A 的行列式值为0。
如图1.30（c）所示的是二元一次线性方程组有无穷多组解的情况，两条直线重合，线性方程组可以表达为：
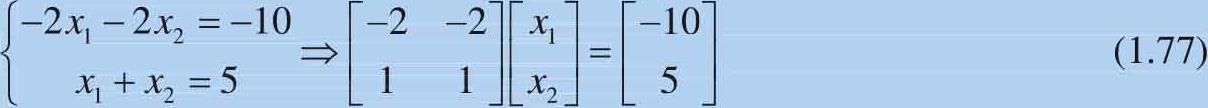
同样，式（1.77）中 A 行列式值也为0。
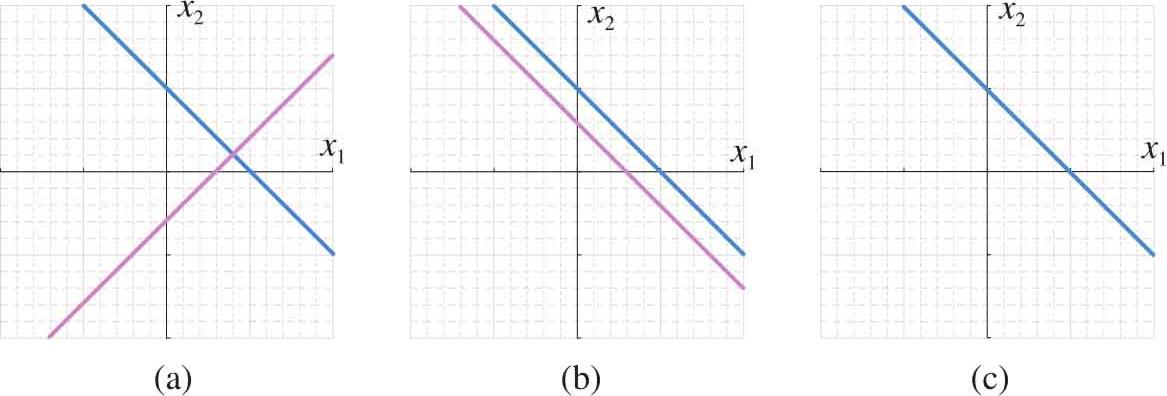
图1.30 二元一次线性方程组有唯一解、无解和有无穷多组解三种情况
三元一次线性方程组可以有唯一解，这种情况，三个平面相交于一点。三元一次线性方程组无解的情况有很多。三元一次线性方程组平面重合，或者相交于一直线时，方程组有无数组解。求解线性方程组的方法有很多，前文讲过的LU分解、Cholesky分解和SVD分解都可以用来求解线性方程组，此处就不再赘述。线性方程组和线性相关性有着密切关系，有关线性相关性内容，丛书第四本会介绍。