




LU分解 (LU decomposition),即将一个矩阵 A 分解为一个 下三角矩阵 (lower triangular matrix) L 和一个 上三角矩阵 (upper triangular matrix) U 的乘积:

如图1.26所示就是式(1.58)的LU分解:

MATLAB进行LU分解的代码为:[ L , U ]=lu( A )。再次强调,图1.26中矩阵运算的乘号×是矩阵乘法的意思,不是内积也不是外积。
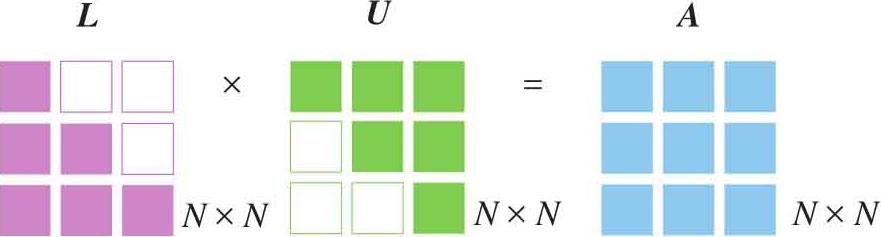
图1.26 LU分解示意图
Cholesky分解 (Cholesky decomposition, Cholesky factorization)是LU分解的特例。在第二本书蒙特卡罗模拟时反复使用过这种方法。Cholesky分解把矩阵分解为一个下三角矩阵以及它的转置矩阵的乘积:

也就是:

并非所有矩阵都可以做Cholesky分解,只有 正定矩阵 (positive-definite matrix)才可以。正定矩阵的特征值均为正。MATLAB进行Cholesky分解的命令为chol()。chol()函数默认获得 R 矩阵,使得 A = R T R 。
Cholesky分解如图1.27所示。
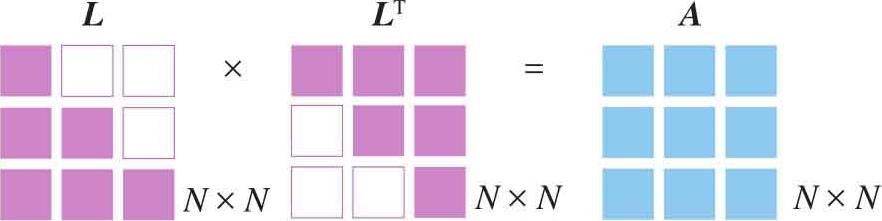
图1.27 Cholesky分解示意图
为使得矩阵 L 对角元素为1,常把Cholesky分解,进一步扩展为 LDL分解 (LDL decomposition):

LDL分解可以表达为:

MATLAB对应的命令为ldl()。如图1.28所示为LDL分解。

图1.28 LDL分解示意图
还有一种常用的矩阵分解叫作 奇异值分解 (singular value decomposition),简称SVD分解,如图1.29所示:

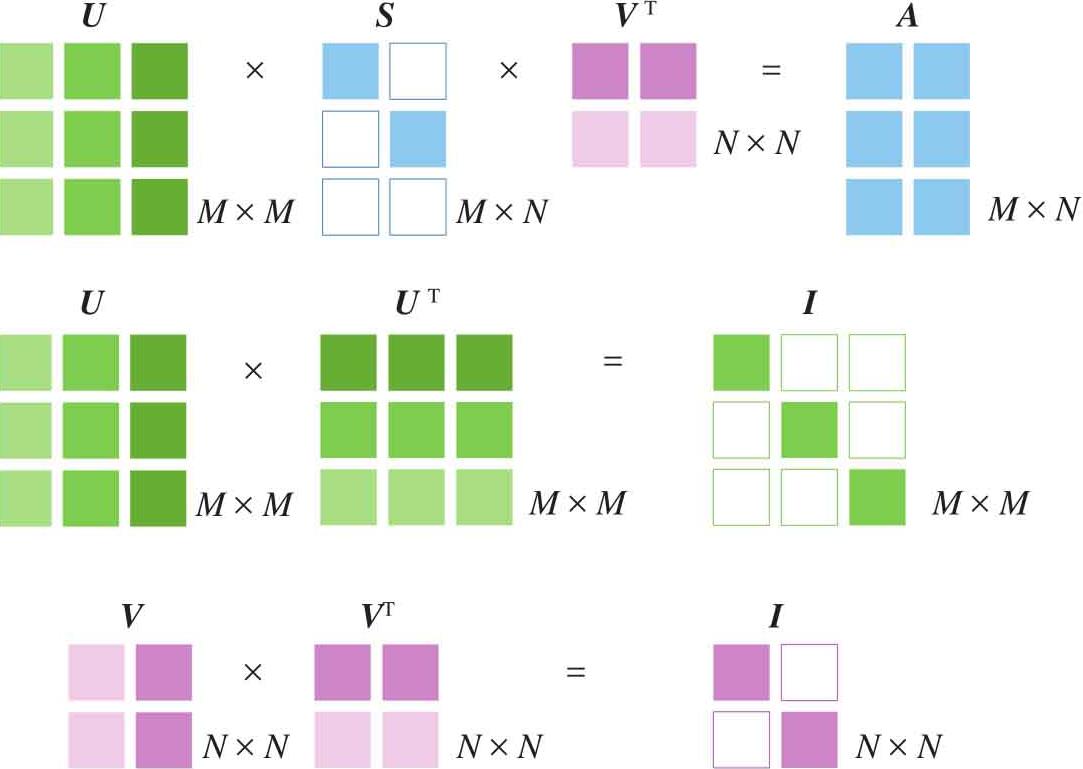
图1.29 SVD分解示意图
其中, A 不一定是方阵,也可能是其他矩形阵。分解结果中 U 和 V 为方阵, S 和 A 的形状相同。 U 和自己转置的乘积为单位矩阵。同样, V 和 V 转置的乘积也是单位矩阵。
下面简单介绍一下SVD手动求解过程,以式(1.64)所示的矩阵为例:

为求解 V ,先求解 A 的转置和 A 的乘积 AA T :
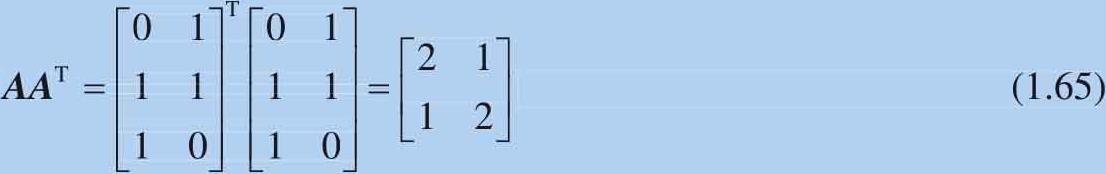
进一步得到 AA T 特征值和特征向量:
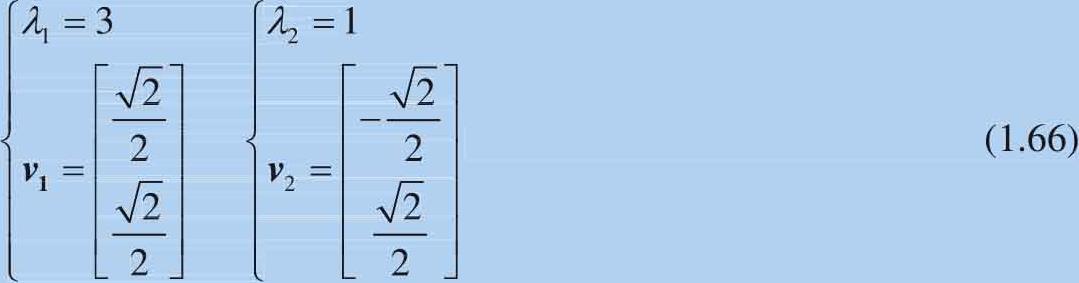
然后再求解 AA T :

同时得到 A T A 特征值和特征向量:

奇异值矩阵如下:

因此对 A 进行SVD分解可以得到:
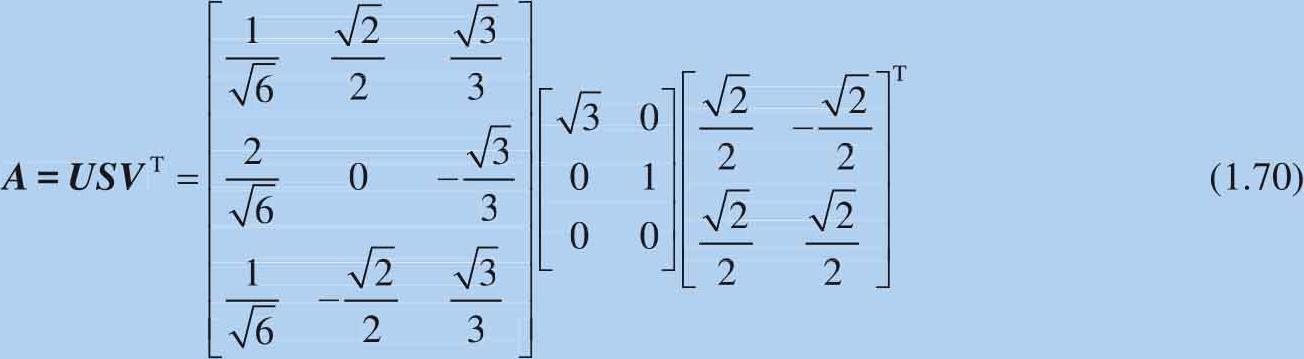
读者可以用MATLAB命令[ U , S , V ]=svd( A )验证结果。下文会介绍SVD用于求解 正交回归 (orthogonal regression)和 主成分分析 (principal component analysis, PCA)。SVD分解在数据处理、机器学习等领域应用极其广泛,请读者格外注意SVD应用。