矩阵转化 (matrix transformation)是本书中矩阵运算的重点,矩阵转化可以将很多抽象的矩阵运算以几何方式展示出来。请读者注意,MATLAB函数的输入变量会采用特定的行向量或者列向量形式,与某些书籍的表达或推导并不完全一致。
若数组 D 的形状是 L × N ,即 L 行和 N 列。每一列代表一个观测变量,每个观测变量有 L 个观测值。方便起见,令 N =2,假设其分别对应坐标系中的 x 和 y 。这样,数组 D 可由二维平面上的不同点来表达,如图1.10所示。
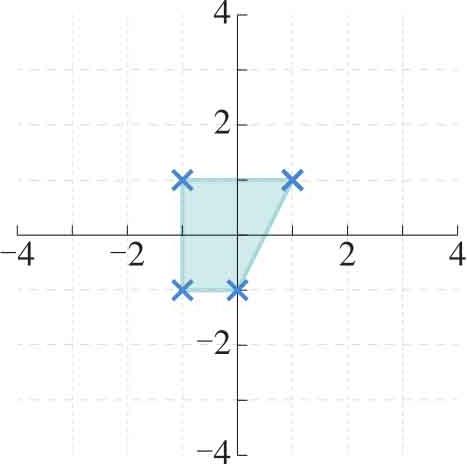
图1.10 原始二维数据按次序首尾相连构成的图形
首先是沿 x 方向 拉伸 (stretching)。对原二维数组 D 在 x 方向 k 倍拉伸,可以通过矩阵运算得到:
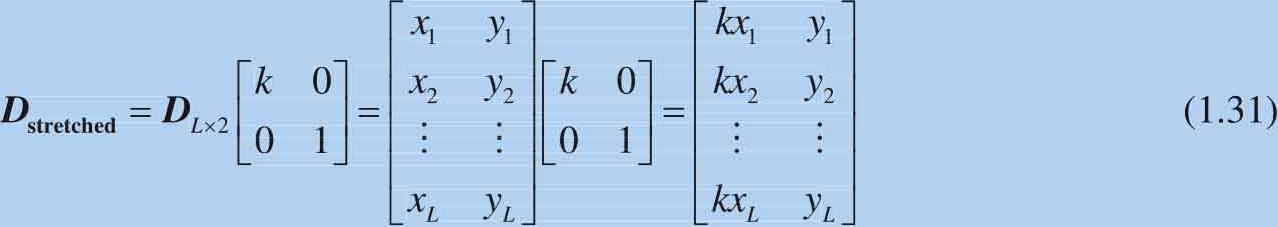
此时式(1.31)中, k >1。如果 k <1,产生的效果就是 压缩 (compressing, squeezing)。拉伸和压缩统称 缩放 (scaling)。如图1.11所示是矩阵缩放运算矩阵的形状关系。再次注意,图中矩阵运算的×,并非向量叉乘,×在这里仅仅表达矩阵相乘。
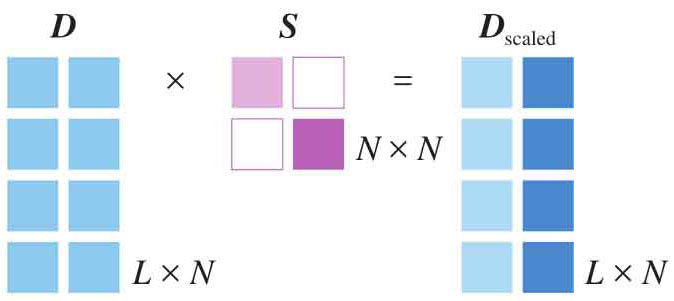
图1.11 形状为 L × N 的数据 D 的缩放计算
如果 x 方向的 缩放系数 (scaling factor)为 a , y 方向的缩放系数为 b ,可以得到:
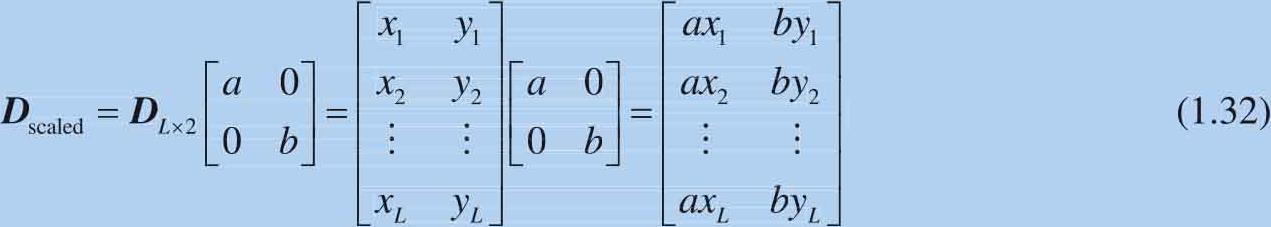
如图1.12(a)所示,当 a 和 b 相等且均大于1,得到的图形和原图像是相似放大关系,也就是等比例放大。如图1.12(b)所示,当 a 和 b 相等且大于1小于0,得到的图形和原图是相似缩小关系,是等比例缩小。如果 a 和 b 大于0,但是不相等,得到的缩放效果则是非等比例的。图1.13所示是非等比例缩放的三个例子。
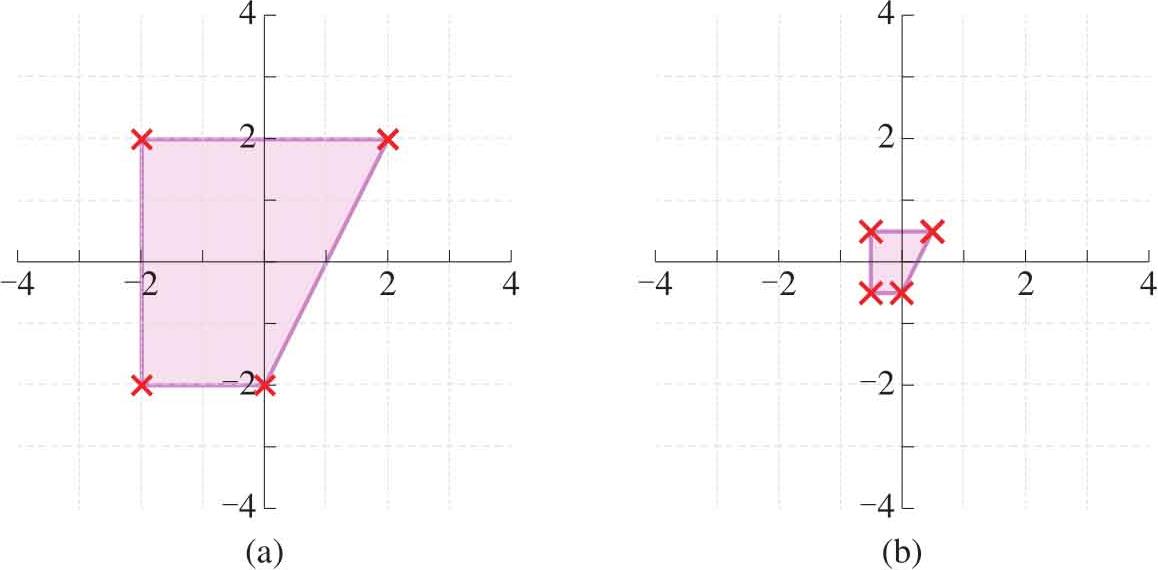
图1.12 等比例缩放
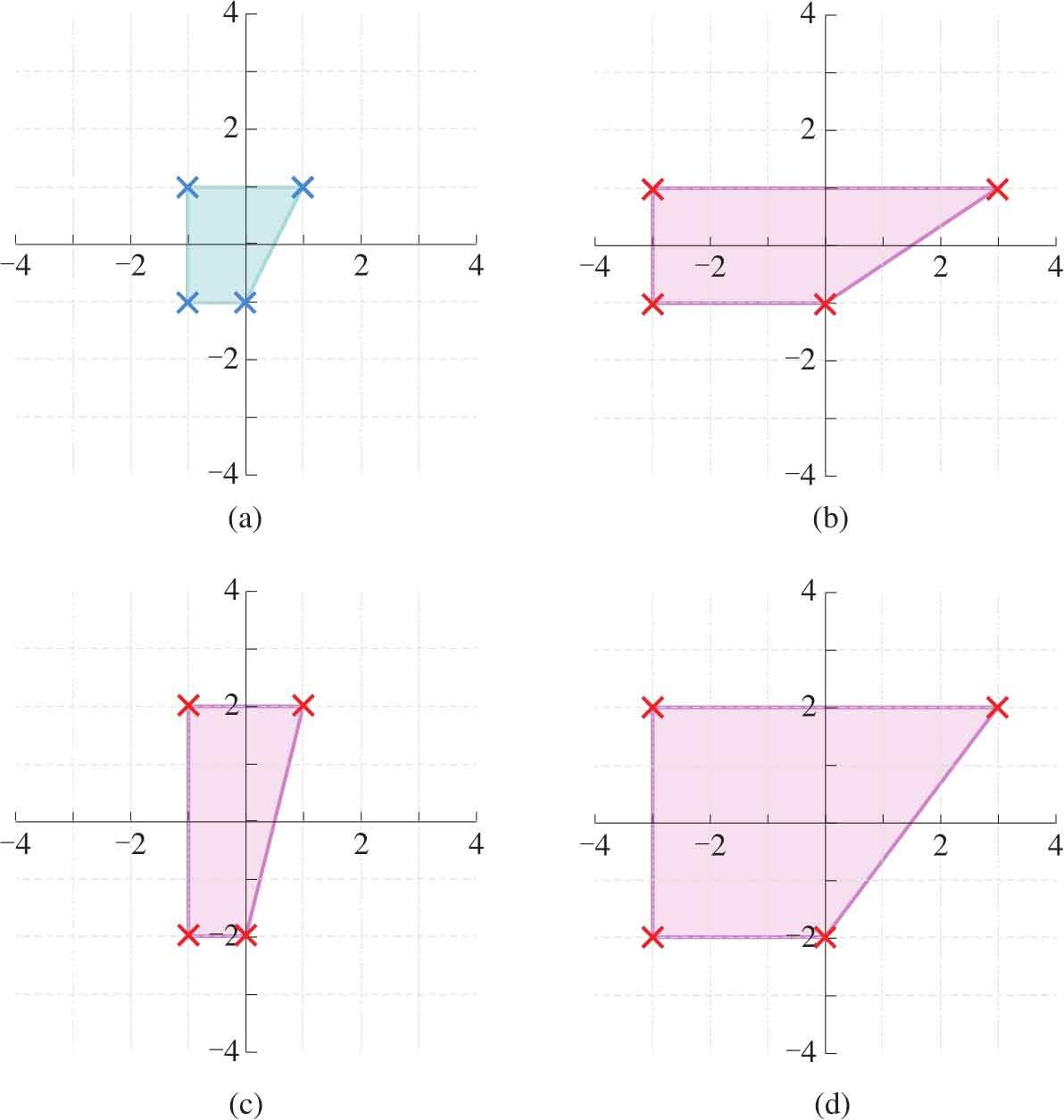
图1.13 非等比例缩放
如果缩放比例 a 或 b 小于0会产生什么效果?如图1.14所示,分为三种情况把矩阵做一次分解。
情况一:

情况二:

情况三:

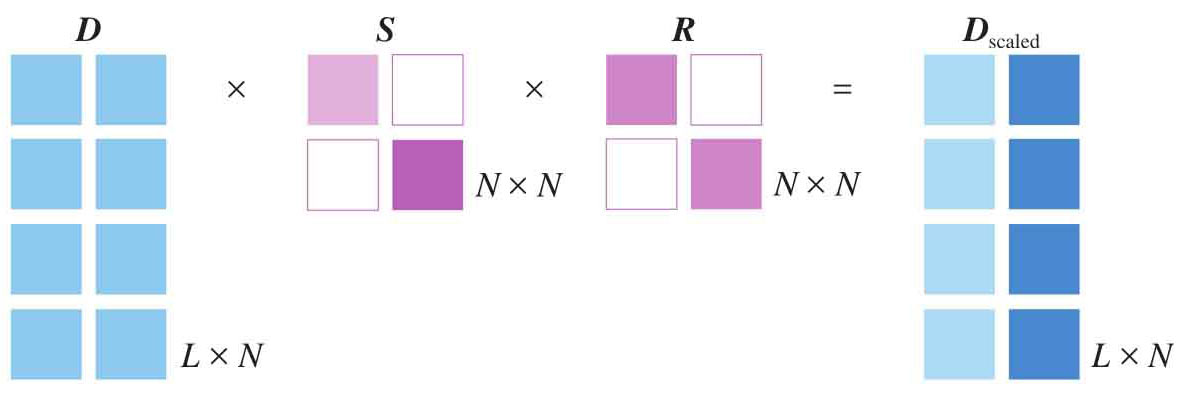
图1.14 形状为 L × N 数据 D 先缩放然后对称运算
很明显,如图1.15所示,经过 R =[-1,0;0,-1]处理得到的图形和原图形 以原点中心对称 (central symmetry with respect to origin),相当于图形绕原点顺时针旋转180°。而[-1,0;0,1]的效果是以 y 轴做镜像对称。[1,0;0,-1]产生的效果则是以 x 轴做镜像对称。这里初次提到旋转和对称的特殊情况,随后会进一步介绍。
如果数据 D 的形状为 N × L ,也就是 N 行, L 列。如图1.16所示,当 N =2时,对数据进行拉伸处理,可以这样处理:

相当于:
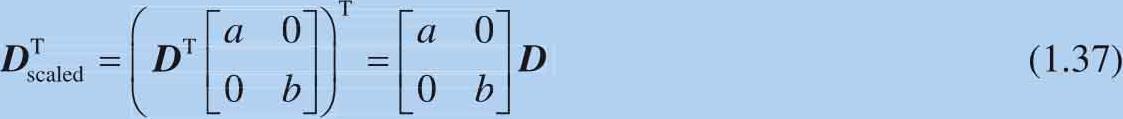
由于[ a ,0;0, b ]是对角阵,因此它的转置结果还是本身。
下面继续旋转操作的话题。一个坐标点( x , y )绕原点 顺时针 (clockwise)旋转 θ ,可以通过式(1.38)求得:

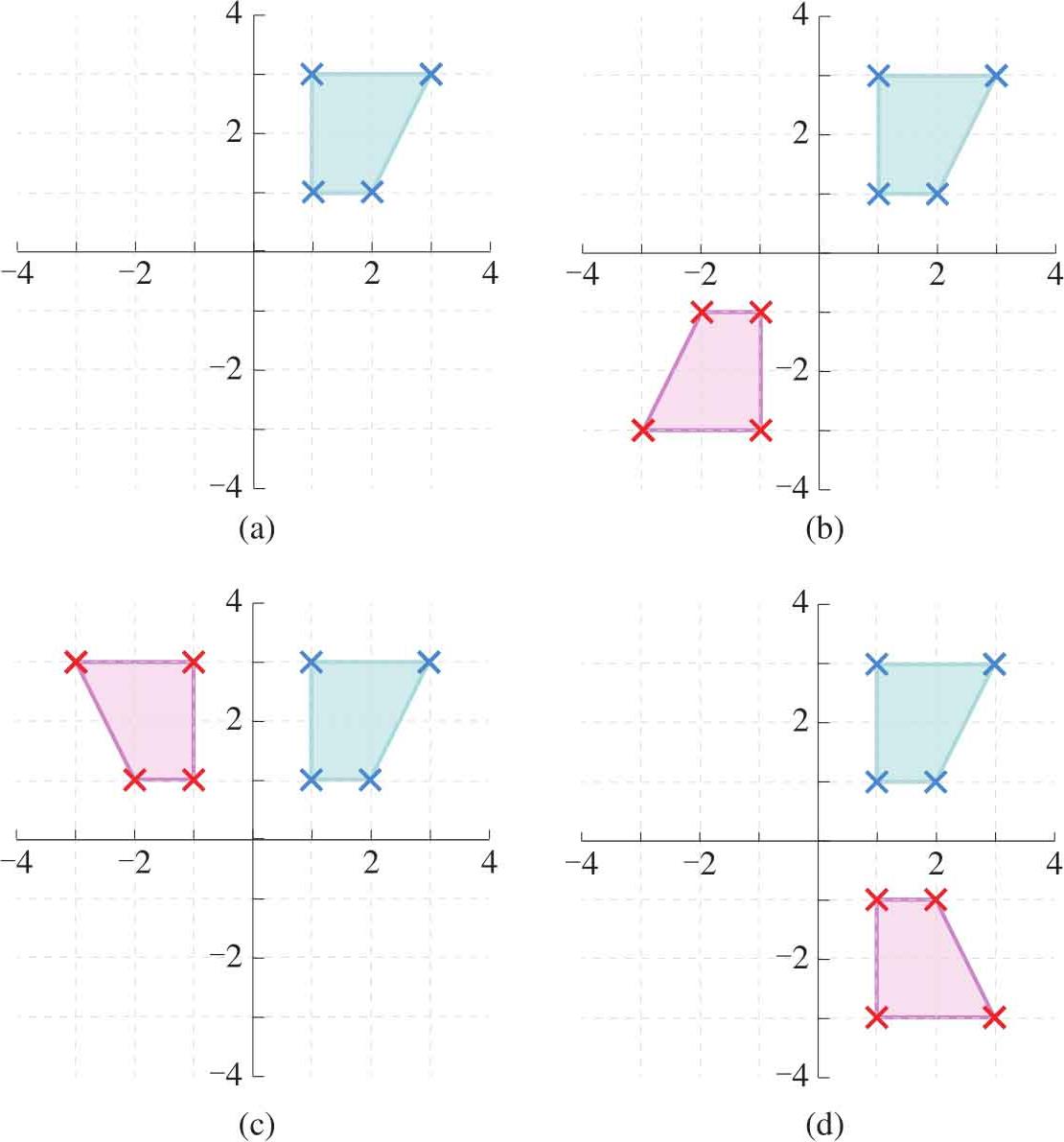
图1.15 中心对称、 y 轴对称和 x 轴对称

图1.16 形状为 N × L 的数组 D 的缩放计算
形状为 L ×2的数据矩阵 D ,可以通过式(1.39)进行旋转:

如图1.17所示是初始形状分别绕原点顺时针旋转45°、90°和120°三种情况。请读者自行编写MATLAB绘制图1.17。
当原始图形旋转90°和180°时,旋转矩阵的具体值如下:

如图1.18所示,向量 a 在极坐标系可以表达为( r , α ),则在正交系中向量 a 的横纵坐标为:

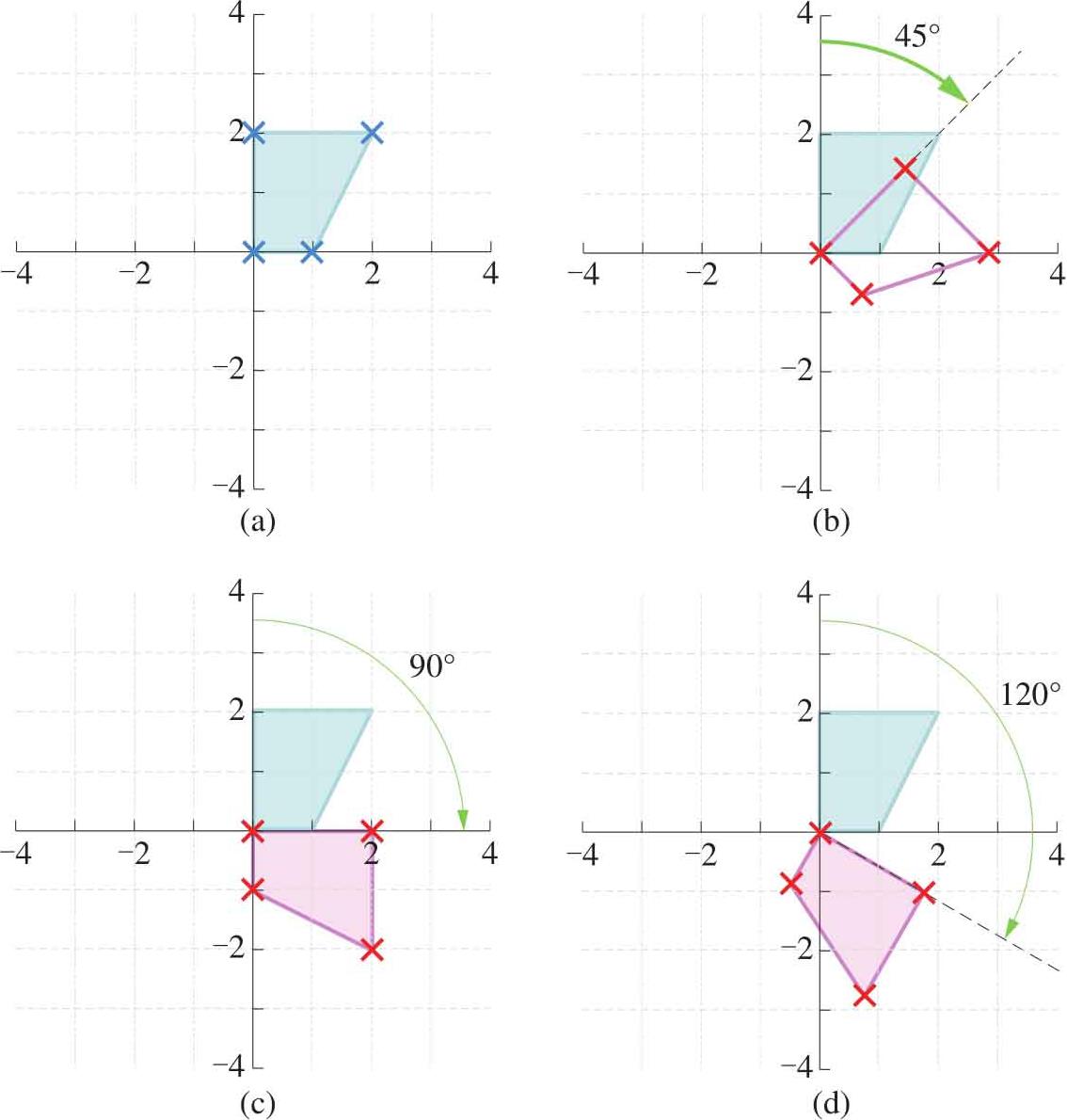
图1.17 平面点绕原点顺时针旋转
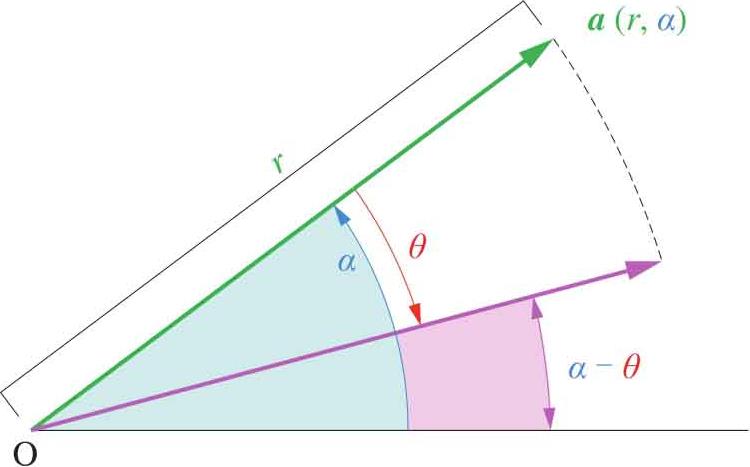
图1.18 极坐标中解释旋转
向量 a 顺时针旋转 θ 后,得到( r,α-θ )。

将向量 a 的极坐标横纵坐标代入式(1.42),可以得到:

式(1.43)整理可得式(1.44):

式(1.44)正是前文采用的旋转操作的矩阵。 D 的 逆时针旋转 (anti-clockwise)可以通过式(1.45)运算完成:
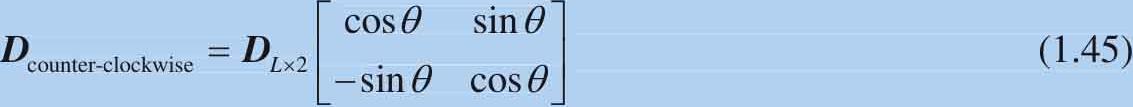
请读者自行编写代码绘制图形绕原点逆时针旋转。如果数据维度以行来表达,进行旋转运算的形式如下:
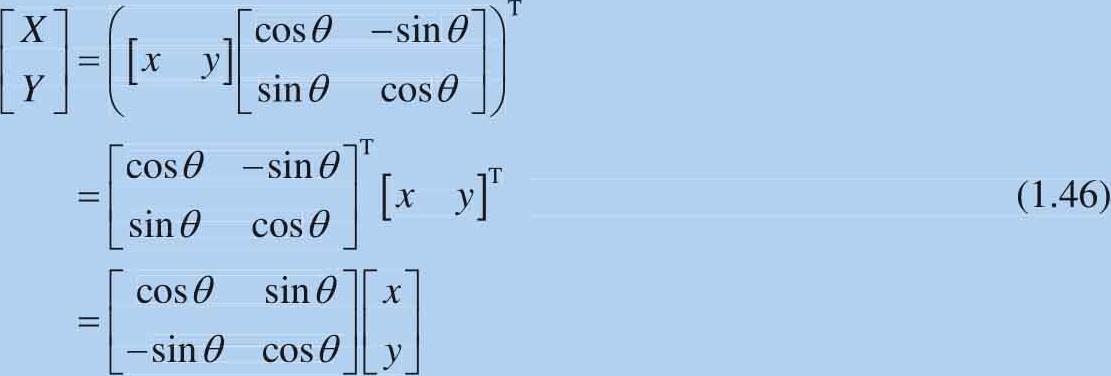
如图1.19所示,是数据先旋转后缩放以及先缩放后旋转得到的不同结果。再次说明,对于两个方阵 A 和 B ,一般情况 AB 和 BA 两种乘积结果不同。上文看到的一个特例是,当 A 和 B 都是对角方阵, AB 和 BA 两种乘积结果相同。
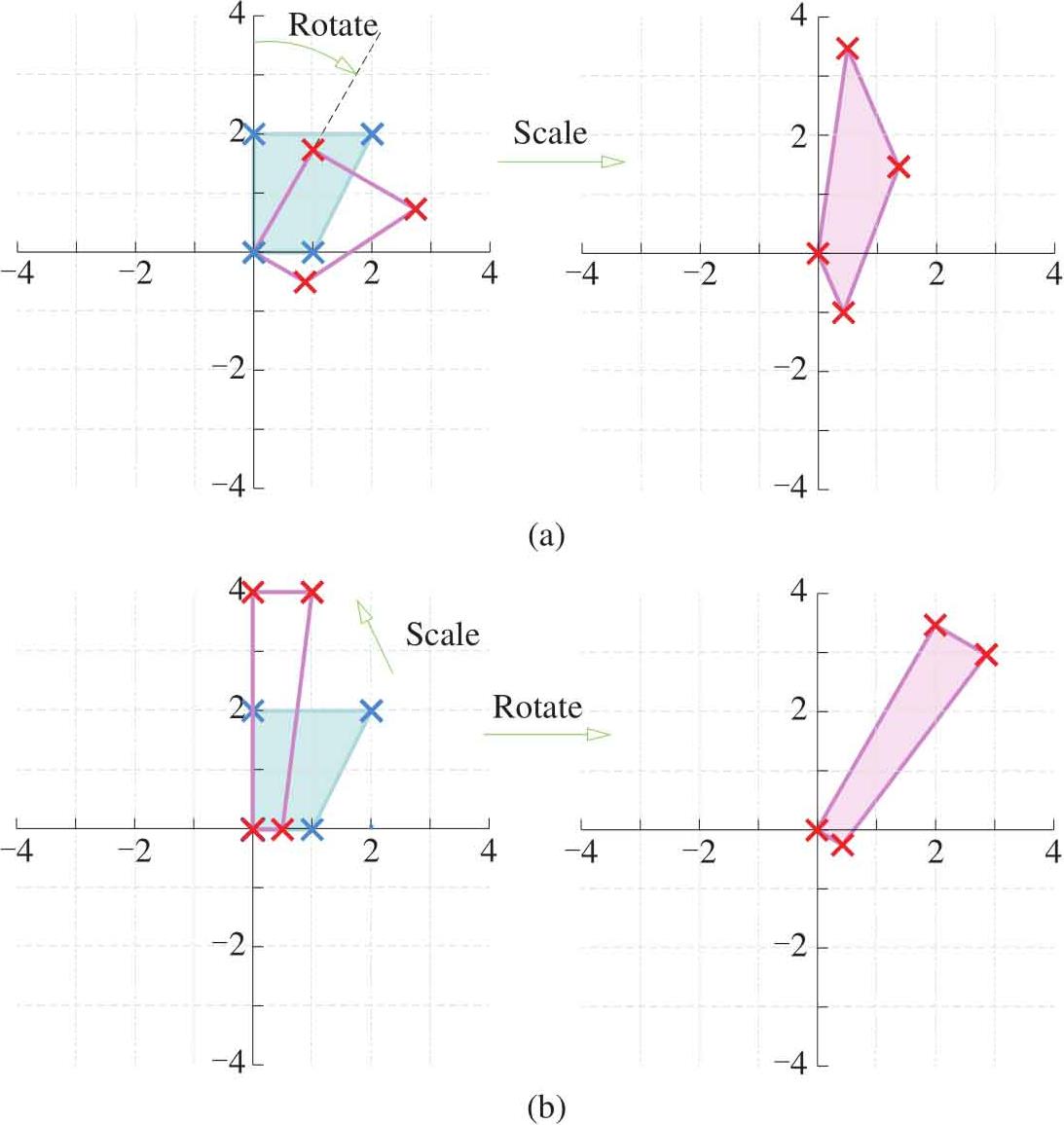
图1.19 先旋转后缩放,和先缩放后旋转
下面研究一下 镜面对称 (reflection)的情况。某一条通过原点的直线方向的向量如下:

沿这条直线镜像得到的数据为:
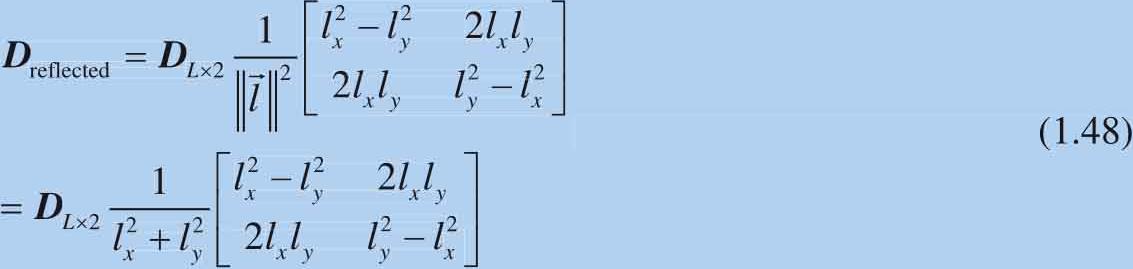
这个2×2的矩阵为对角阵,因此矩阵的转置为其本身。也就是说维度以行来表达时,沿直线镜像得到的数据可以通过式(1.49)计算:
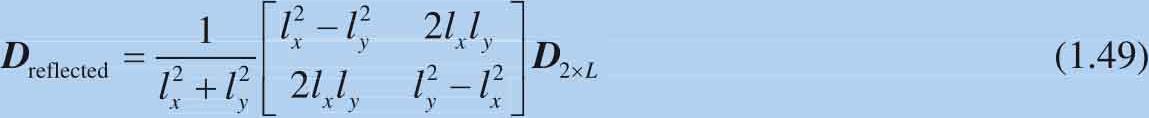
如图1.20所示是四个镜像的例子,镜像直线方向分别是(1,1)、(1, -1)、(1, 2)和(1, -2)。
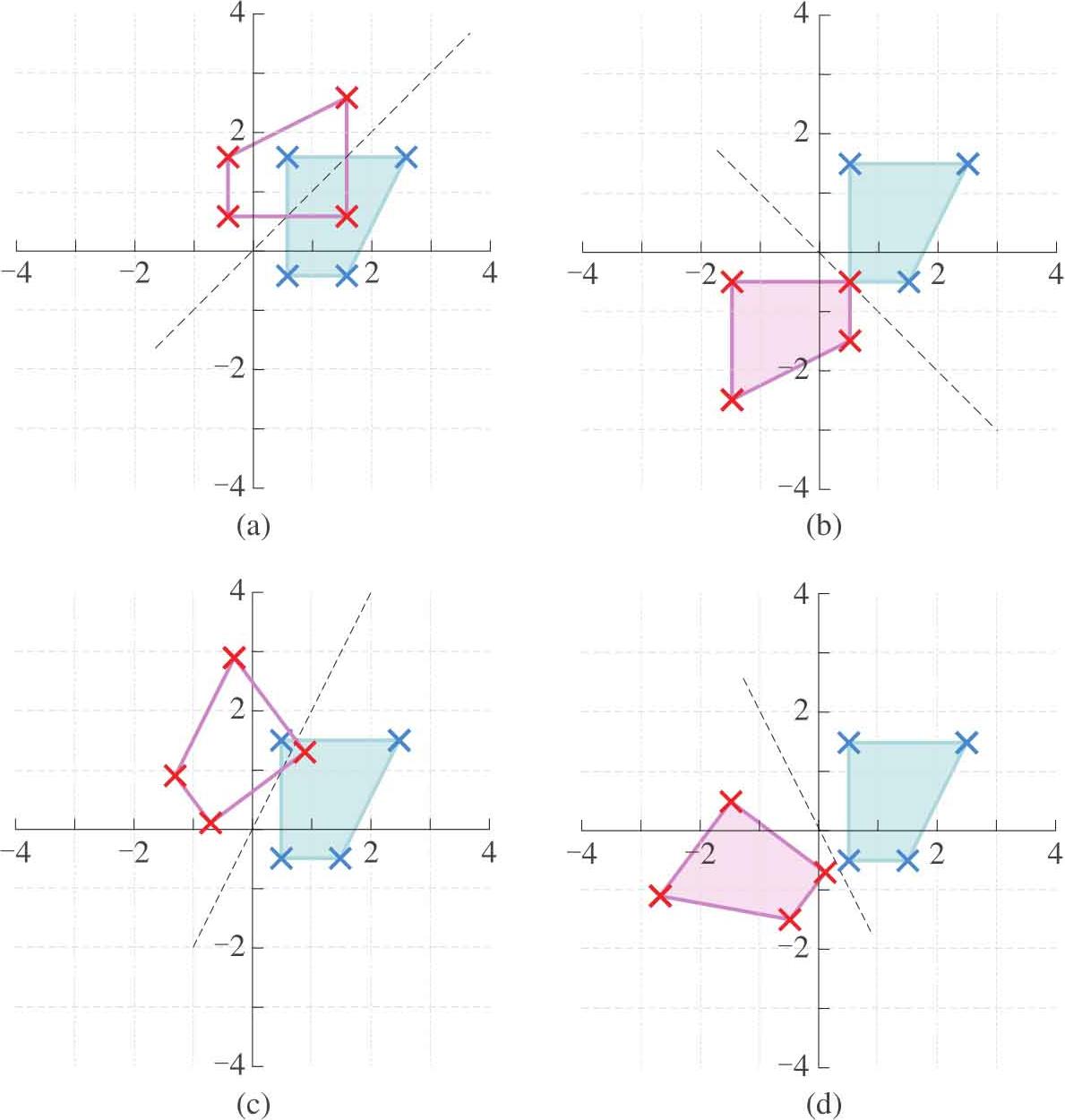
图1.20 四个镜像例子
下面研究 正交投影 (orthogonal projection)情况。某一条通过原点的直线方向的向量如下:

平面点 D 正交投影到上述直线的结果如下:

如图1.21所示是平面点 D 在四条不同直线投影的结果。这种投影方式,在丛书第四本还要深入讨论。
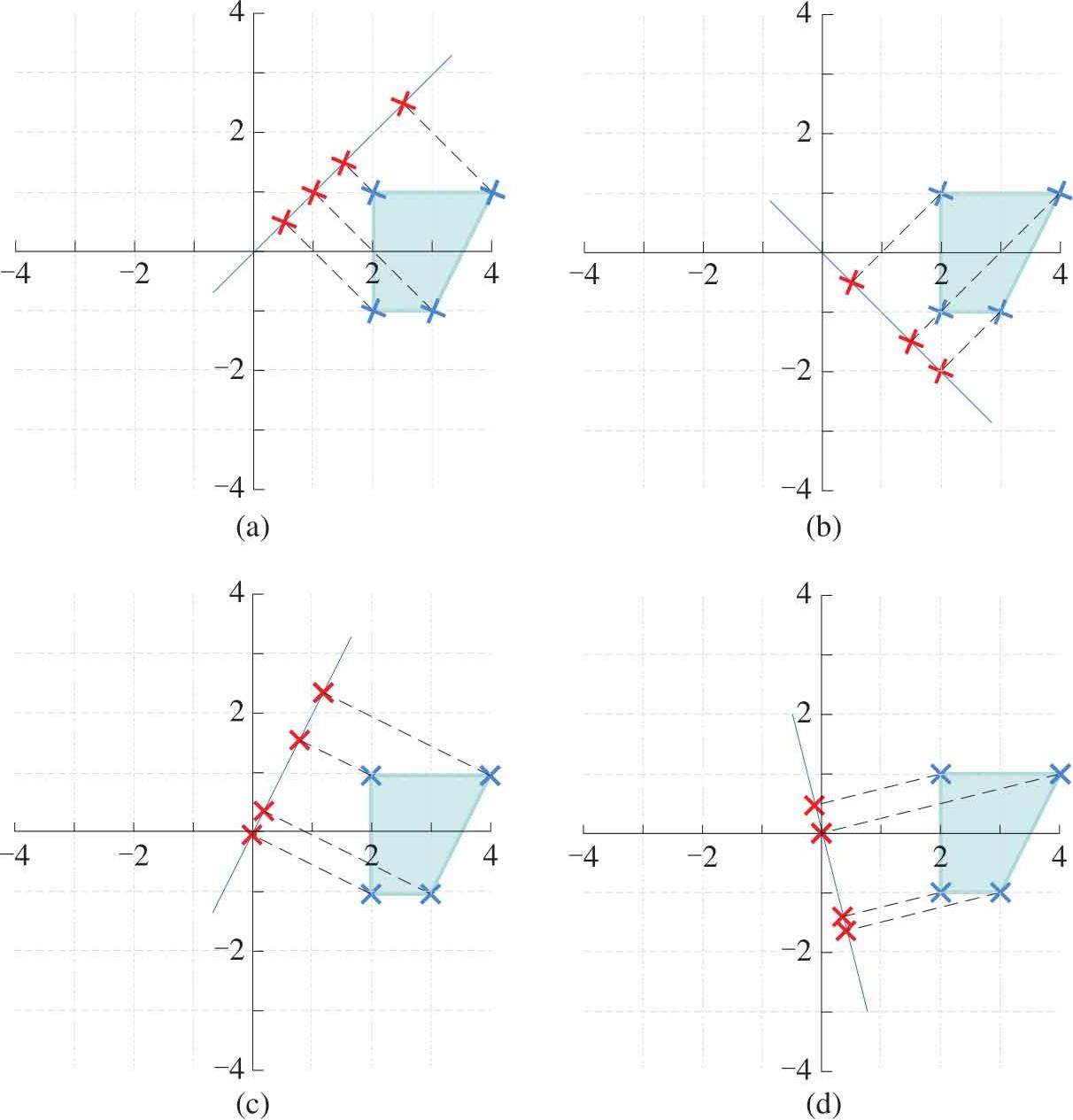
图1.21 四个正交投影例子
两个特别的投影是向横轴和纵轴投影。完成向 x 轴正交投影的矩阵为:

完成向 y 轴正交投影的矩阵为:

如图1.22所示是图像顶点在 x 轴和 y 轴投影。
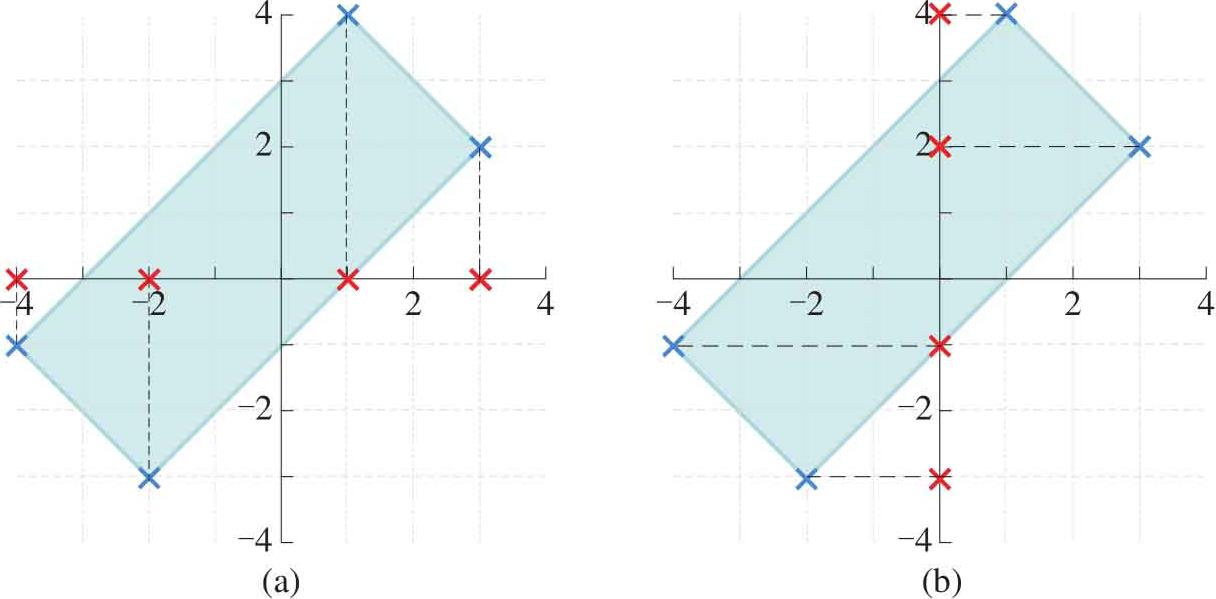
图1.22 向 x 和 y 轴正交投影
本节最后讨论一下 剪切转换 (shear transformation)。沿着 x 轴方向的剪切转换矩阵为:

式中 θ 为剪切角。
如图1.23所示是四个沿着 x 轴方向剪切转换的例子。沿着 y 轴方向的剪切转换矩阵为:

如图1.24所示是两个沿 y 轴方向剪切转换的例子。
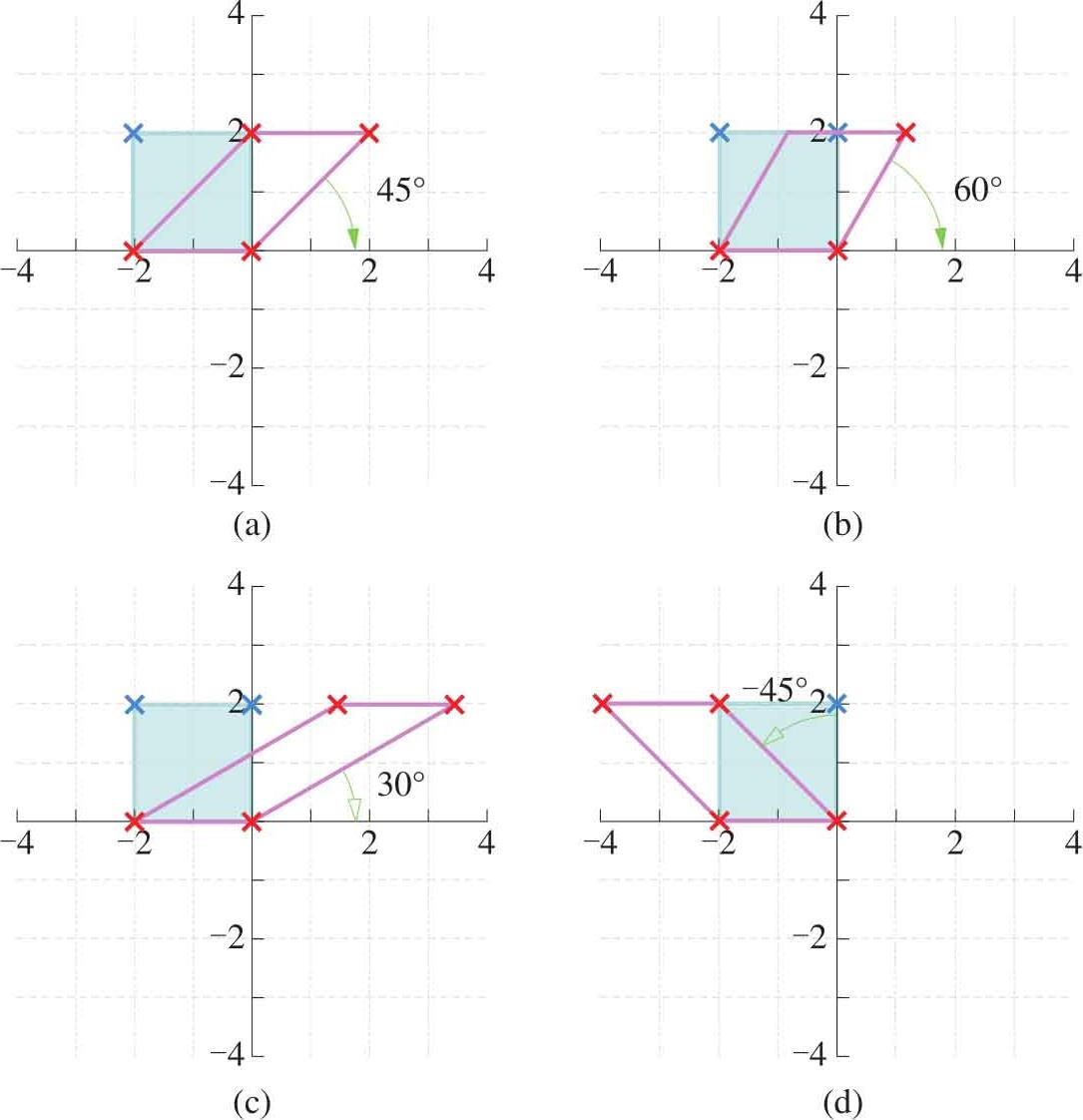
图1.23 沿 x 轴方向剪切转换
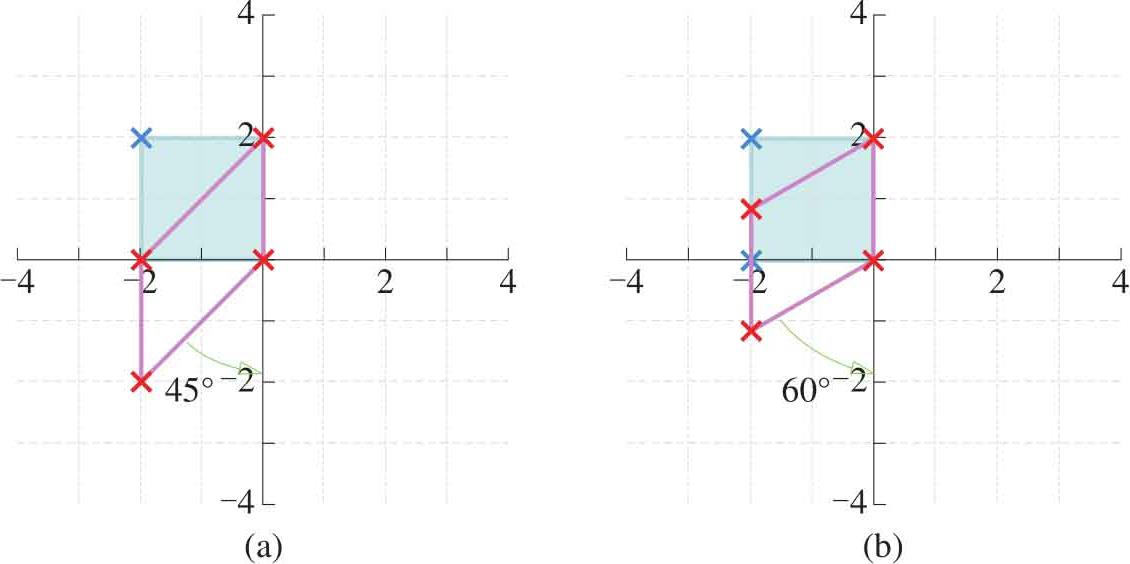
图1.24 沿 y 轴方向剪切转换
式(1.56)所示矩阵完成的转换类似于剪切转换:

使它能保证某个方向上的长度不变。这个长度就是转换点到原始点在 x 轴投影点距离,该距离和原始点到 x 轴投影点距离相等;我们称其为等长度剪切。如图1.25所示是四个相关的例子。
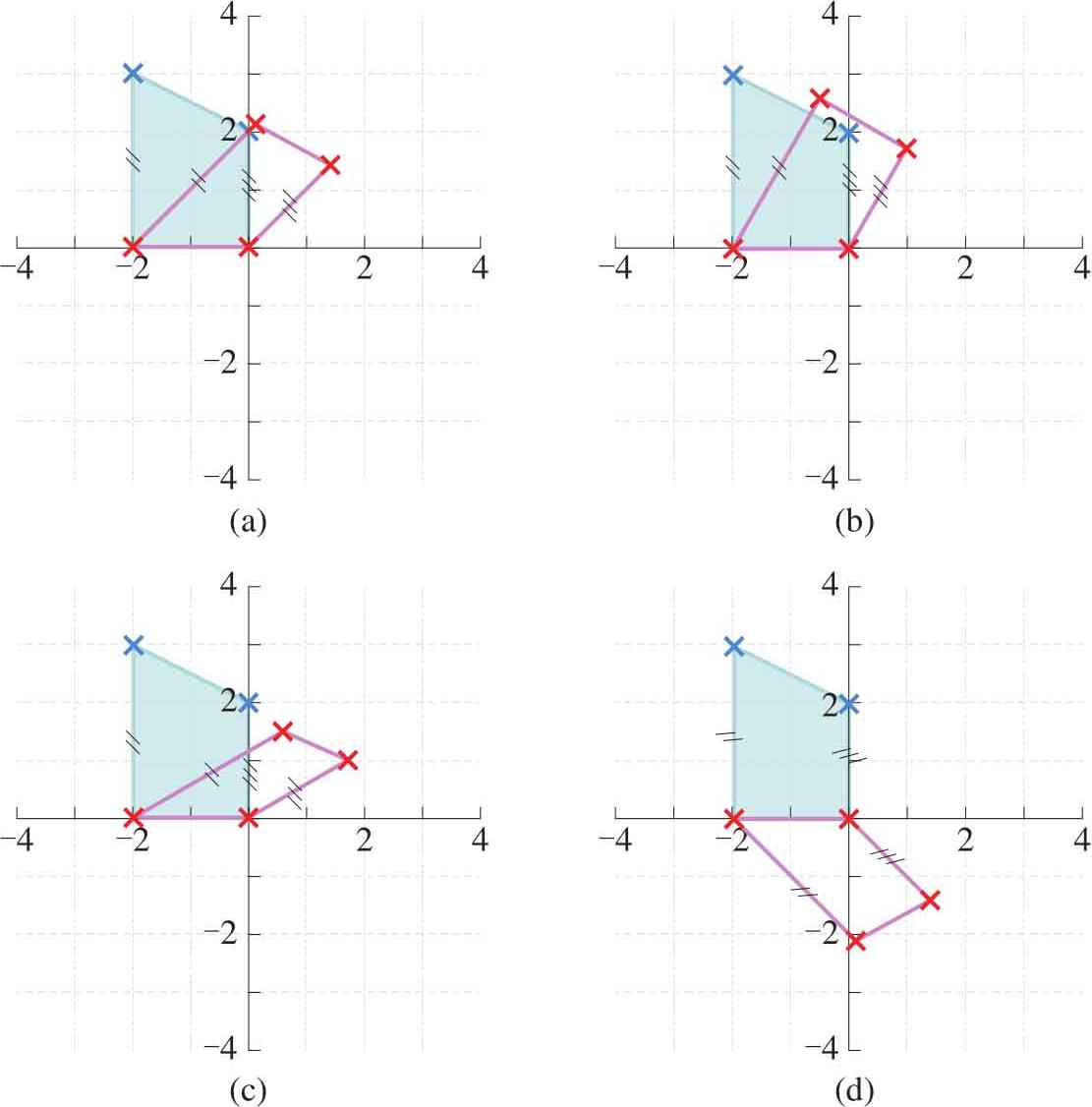
图1.25 沿 x 轴等投影长度剪切
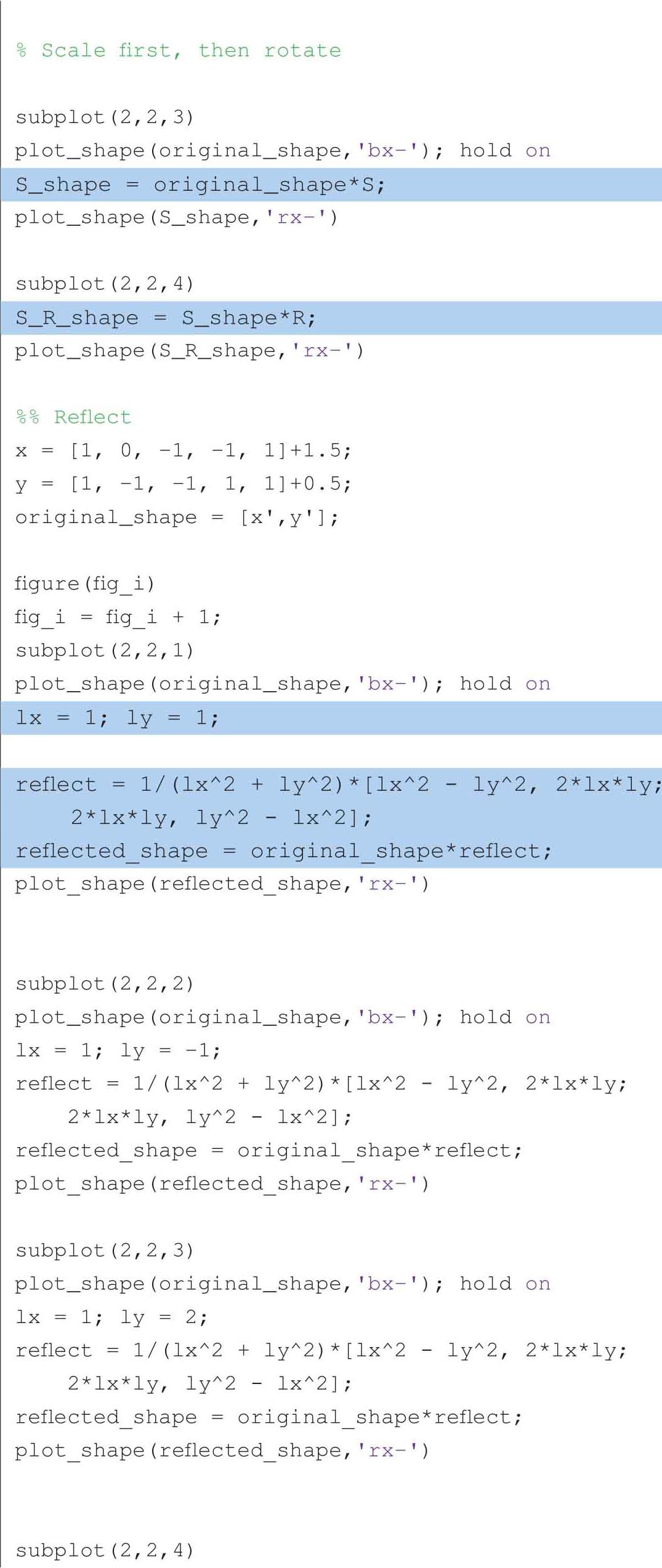
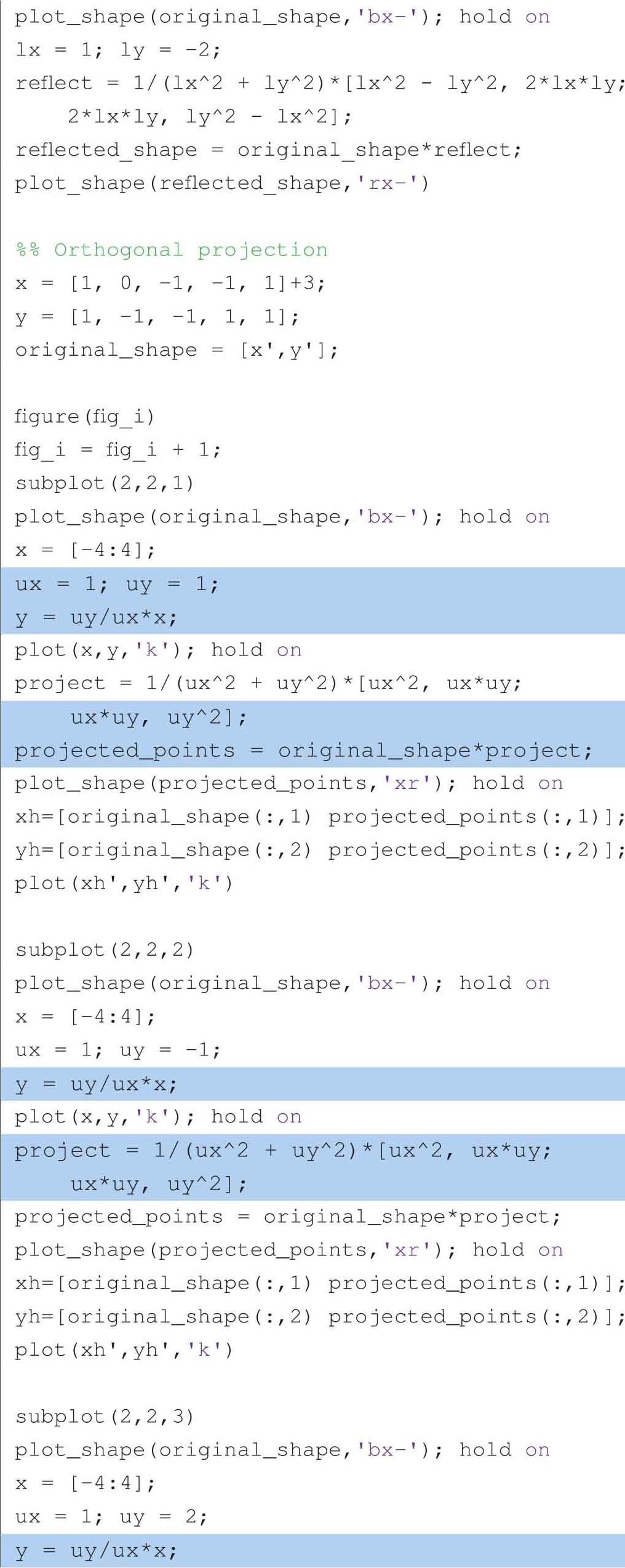
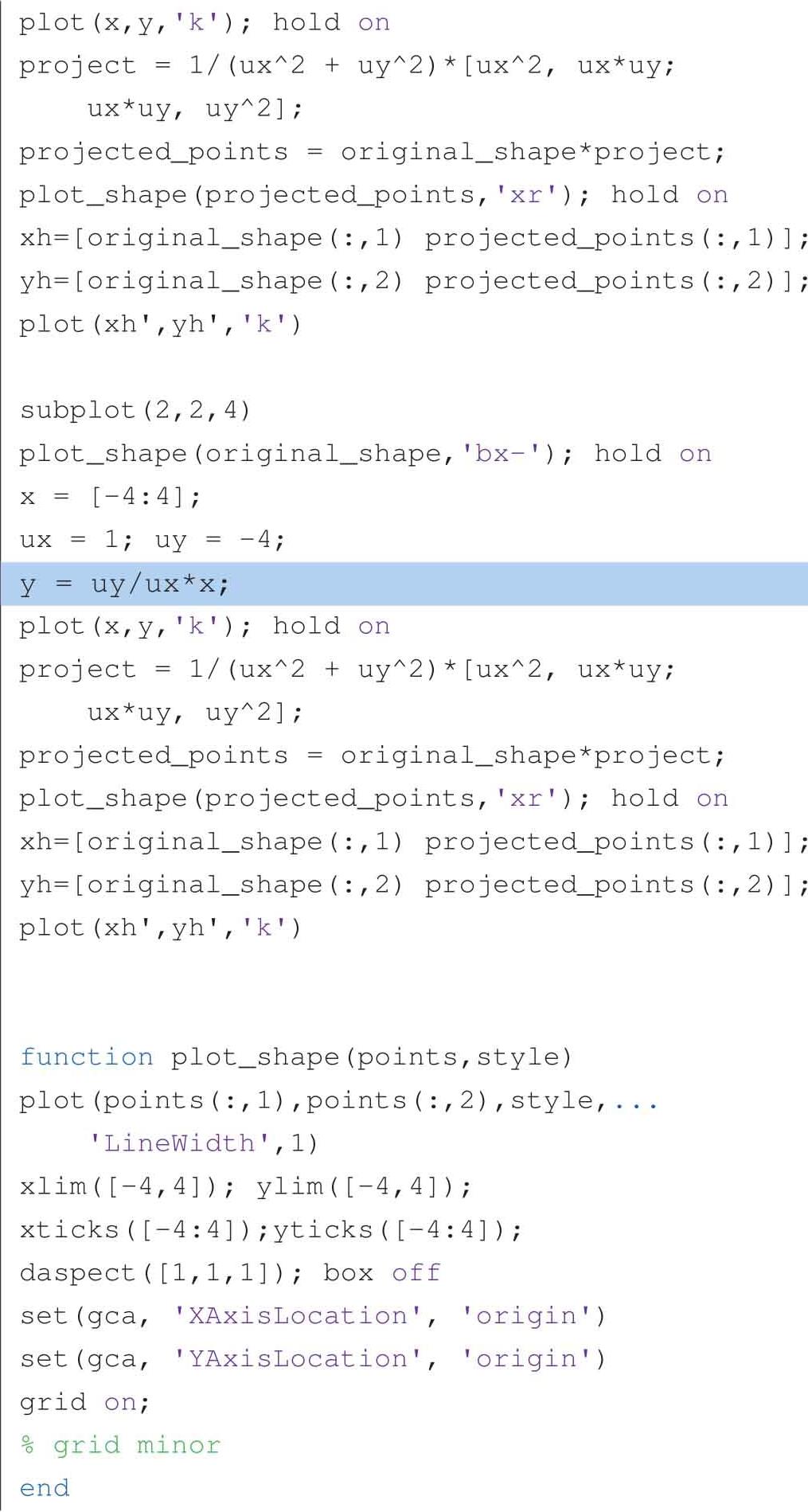
以下代码可以获得图1.17、图1.19、图1.20和图1.21。