




北京农业生产功能演进与经济增长、消费需求之间的关系如何?相互影响程度如何?本节采用协整理论和Grange因果关系分析模型,对北京农业生产功能演进与经济增长、消费需求等之间的关系进行实证分析。
变量指标选取原则:一是保证数据的可获得性;二是保证数据的权威性,尽量使用官方数据;三是在力求全面反映影响农业生产功能演进的因素影响前提下,指标选取尽可能精简。
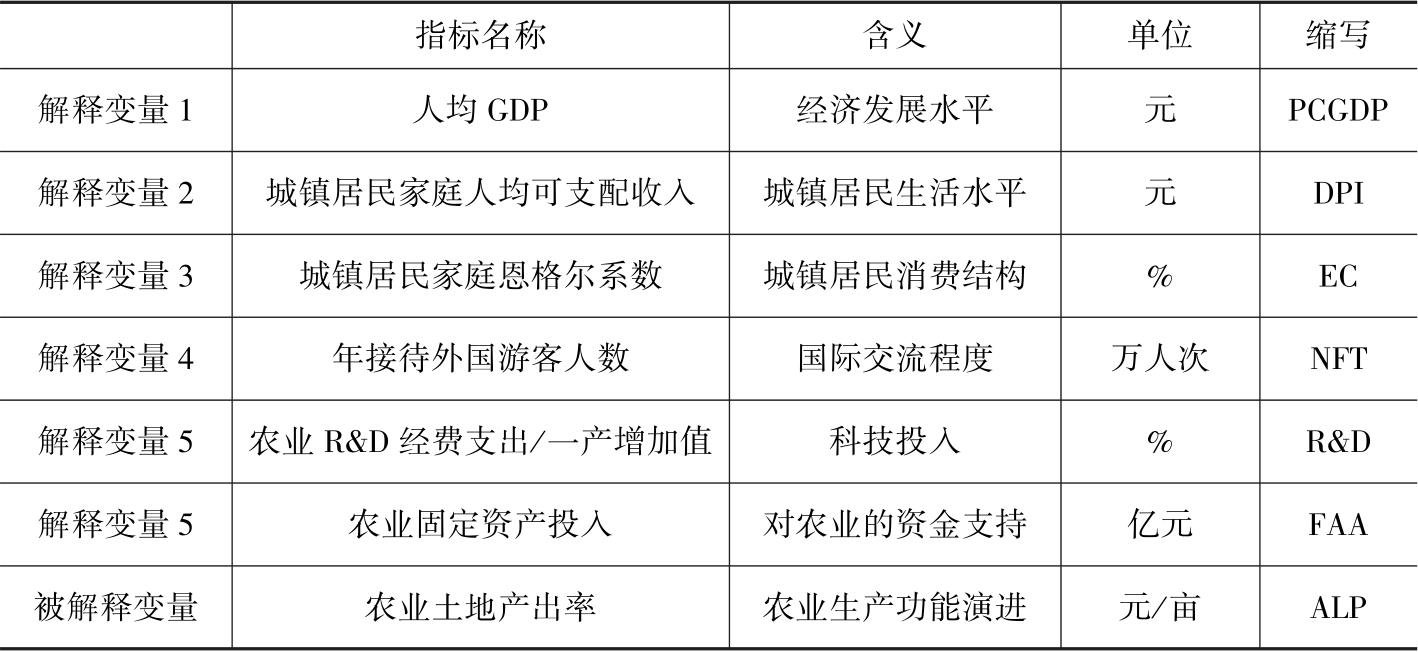
选取人均GDP作为衡量经济发展水平的指标;城镇居民家庭人均可支配收入表征居民的购买力,是衡量城镇居民收入水平和生活水平的统计指标;选取城镇居民家庭恩格尔系数作为表征城镇居民消费结构的指标;选取年接待外国游客人数作为表征北京国际交流程度的指标;选取农业R&D经费支出占一产增加值比重表征科技对农业发展的支撑;选取农业固定资产投入表征对农业的资金支持,对农业生产的政策支撑较难用定量数据描述,定量分析中暂不考虑;选取农业土地产出率作为表征农业生产功能演进的指标(见表2-8)。理由如下:农业生产功能的变化最根本的体现是农业生产率的变化,衡量农业生产率的指标有农业劳动生产率和农业土地产出率。农业劳动生产率表达了劳动支付与报酬获取之间的关系,侧重生产关系,如规模经营提高农业的劳动生产率。农业土地产出率体现为土地投入与产出成果之间的关系,从以粮食生产为主到高效安全农产品生产,这种变化直接体现在农业土地产出率上。
表2-8 农业生产功能演进指标选取
自2014年起,受北京市实施农业“调转节”以及平原造林等政策的影响,农业发展空间受到挤压。为减少政策实施对模型的影响,本研究选取1978—2013年的年度数据作为研究样本,数据来源于《北京统计年鉴》和《中国统计年鉴》。
为了使计算分析具有可比性,消除价格影响,各产出数据均换算为1985年同比价格计算。同时,为了消除数据中存在的异方差,对所有变量均进行对数变换,得到新的变量序列,记为:LNPCGDP、LNDPI、LNEC、LNNFT、LNRD、LNFAA、LNALP。
为消除由于时间序列变量的非平稳性引起的“伪回归”现象,需要对时间序列数据进行平稳性检验。一般在进行规范的平稳性检验之前先绘制序列图,可对数据的平稳性有直接感受。由图2-15可看出,不论是解释时间序列变量还是被解释时间序列变量,在研究期内均表现出上升或下降趋势,从而说明其均值在发生变化,这可能说明,上述6个时间序列变量不是平稳的。
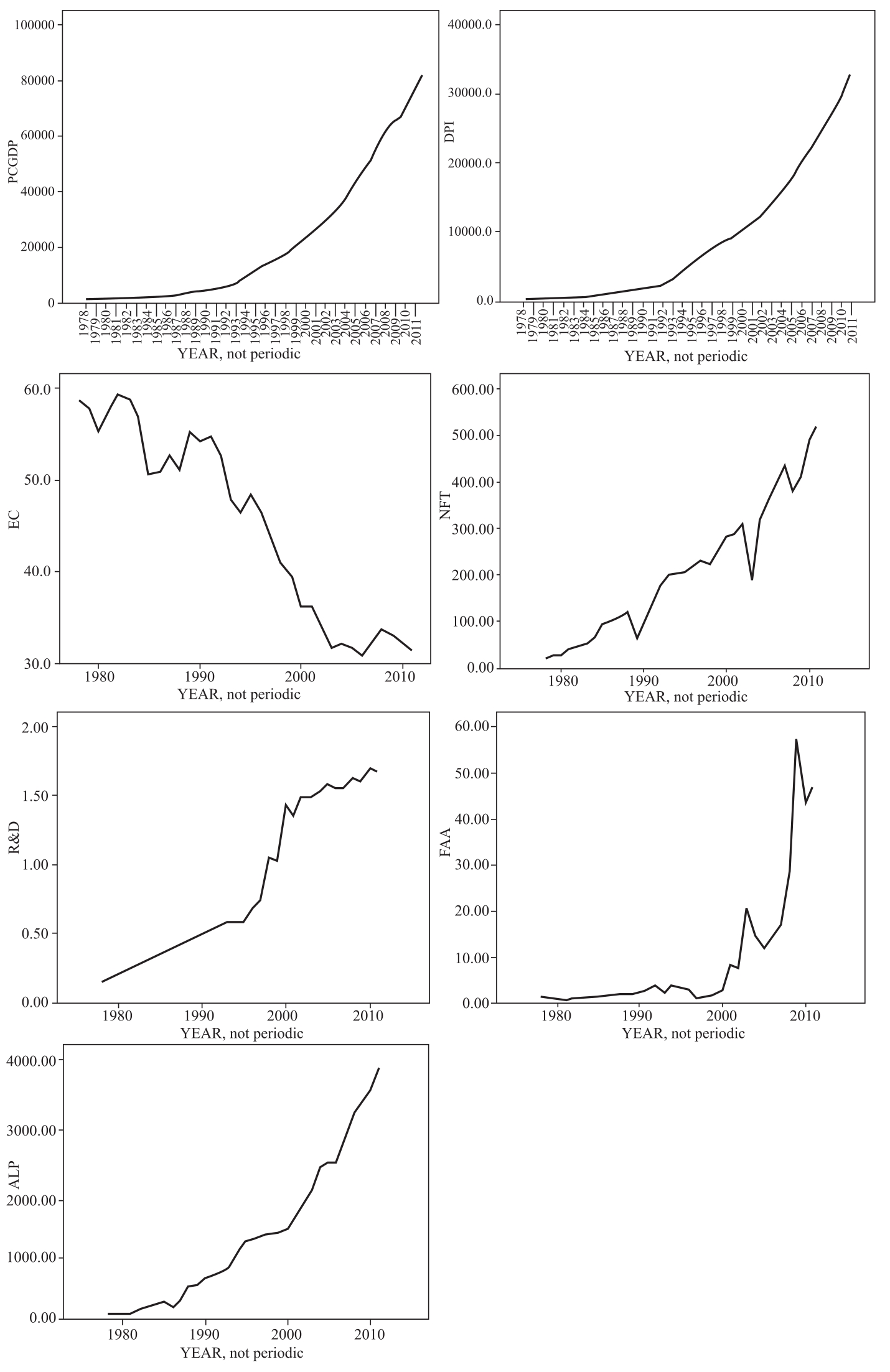
图2-15 时间序列平稳性的图形分析
绘制每个时间序列变量的自相关图和偏相关图(如图2-16所示)。对于平稳时间序列而言,相关图很快会变平,而对非平稳时间序列来说,则消失得很缓慢。受篇幅限制,以下只给出时间序列变量PCGDP的自相关图和偏相关图,可以看出变量PCGDP为典型的非平稳时间序列相关图。
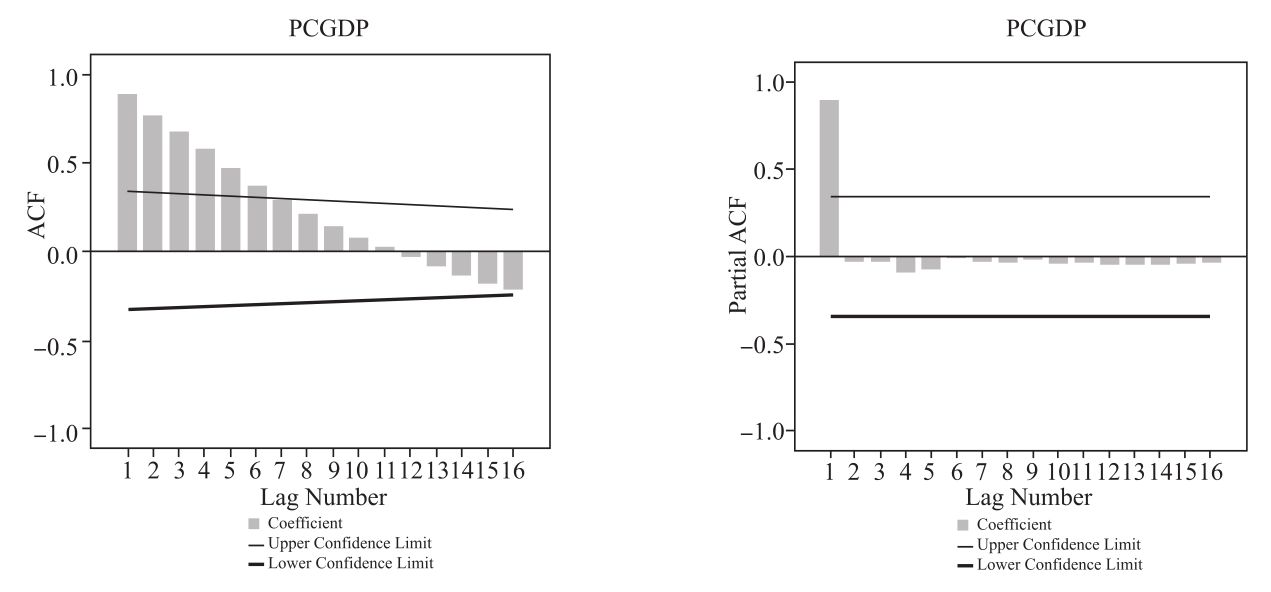
图2-16 人均GDP的自相关图和偏相关图
上一部分在一个非正式的判别水准下,通过时间序列的图形我们初步判断了其平稳性。下面采用ADF单位根检验方法对各变量时间序列平稳性进行严格检验。各变量的相应一阶差分序列记为△LNPCGDP、△LNDPI、△LNEC、△NFT、△RD、△FAA、△ALP,相应的二阶差分记为△ 2 PCGDP、△ 2 DPI、△ 2 EC、△ 2 NFT、△ 2 RD、△ 2 FAA、△ 2 ALP。
利用Eviews软件对变量进行ADF单位根检验。时间序列变量LNPCGDP的一阶差分ADF单位根p值小于0.05,表明在5%的显著水平上接受LNPCGDP为一阶平稳性假设。依次将各个时间变量进行ADF单位根检验,检验结果见表2-9。从表2-9可以看到,所有变量的原序列数据的单位根检验ADF值均大于5%显著水平的临界值,说明所有变量的原时间序列均为非平稳序列,这与上文通过图形猜测结果一致。所有变量的单位根检验结果都表明在5%显著水平上接受一阶平稳性假设,即I(1)序列。
表2-9 各变量时间序列数据的ADF单位根检验结果
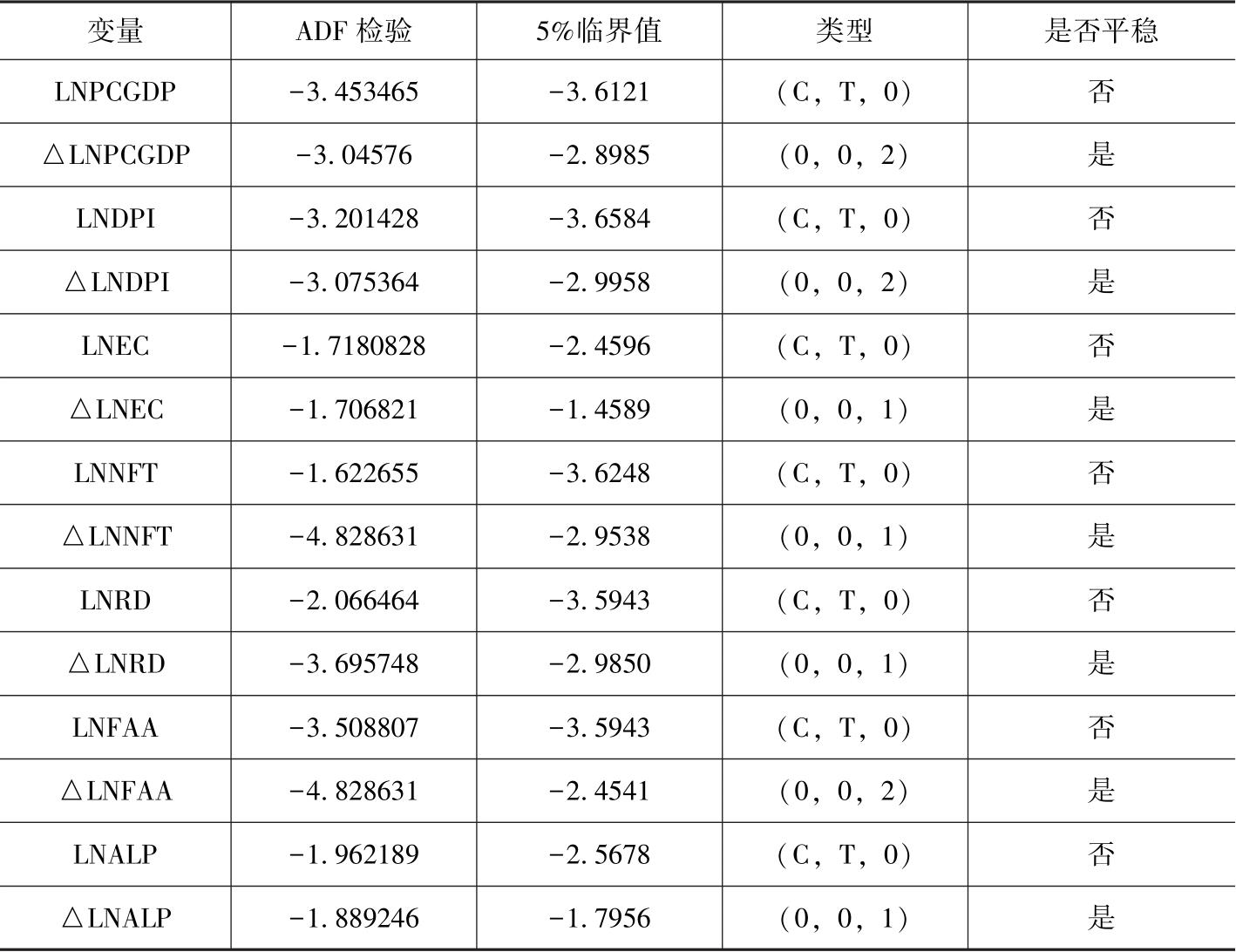
注:①括号内的整数位是根据Schwarz信息准则确定的最优滞后步长,C代表常数项,T代表趋势项,k表示滞后阶数,滞后阶数根据上文的自相关图和偏相关图确定。②ADF检验的原假设H0:含有单位根,则序列是非平稳时间序列。
将一个非平稳的时间序列对另一个非平稳的时间序列进行回归可能导致谬误回归,协整检验可看成为避免“谬误回归”情形而进行的检验。协整是指多个非平稳的经济变量的某种线性组合是平稳的,协整检验主要用来分析时间序列之间的长期均衡关系。需要指出的是,只有所有变量是同阶的,才有必要进行协整检验。对于不同阶的时间序列,不能进行协整检验。
采用Johansen方法建立VAR模型,检验分析变量的协整性。为避免奇异矩阵情形出现,只选取LNPCGDP、LNDPI、LNRD与LNALP进行协整检验。依照AIC准则确定适合的滞后阶数,本次选择最佳的滞后阶段为2。检验结果见表2-10。
表2-10 Johansen协整检验结果
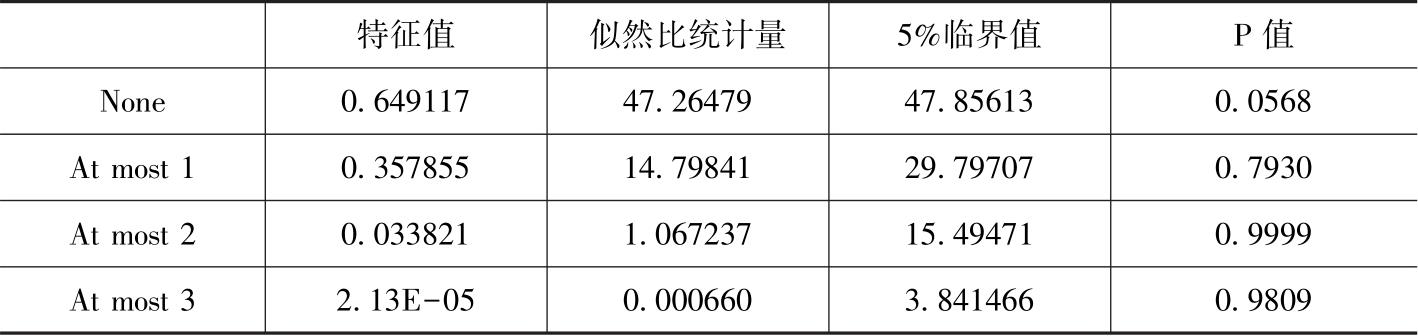
由表2-10可看出,在5%检验水平下,四个似然比统计量的值分别为47.26479、14.79841、1.067237、0.000660,四个似然比统计量均小于其相应的检验临界值,所以变量LNALP与LNPCGDP、LNDPI、LNRD之间存在唯一的协整关系,表明在1978—2011年的样本区间内,各变量之间存在一个长期均衡关系。经标准化处理得到协整参数向量的系数估计值,写成矩阵形式为:T=(1.00,0.05,-0.14,-4.02,-4.96)。由此可以将变量之间的长期均衡关系用方程表示如下:
LNALP t =4.96+0.05LNPCGDP t +0.14LNDPI t +4.02LNRD t
上述长期均衡关系方程显示,1978—2013年间,北京农业生产功能与人均GDP、城镇居民家庭人均可支配收入、农业R&D支出占一产增加值比重存在长期的均衡关系。农业生产功能与人均GDP、城镇居民家庭可支配收入、农业R&D支出均呈正相关关系。北京农业生产功能对人均GDP、城镇居民可支配收入、农业R&D支出比重的长期弹性分别为-0.05、0.14和4.02,即人均GDP每变动1%,农业土地产出率将负向变动0.05%。城镇居民家庭可支配收入每变动1%,农业土地产出率将正向变动0.14%。农业R&D支出比重每变动1%,农业土地产出率将正向变动4.02%。由此可以看出,农业R&D支出比重对农业生产功能的拉动作用最大,其次是城镇居民家庭人均可支配收入。
土地产出率对照见表2-11。
表2-11 土地产出率对照(2010年,现价美元)
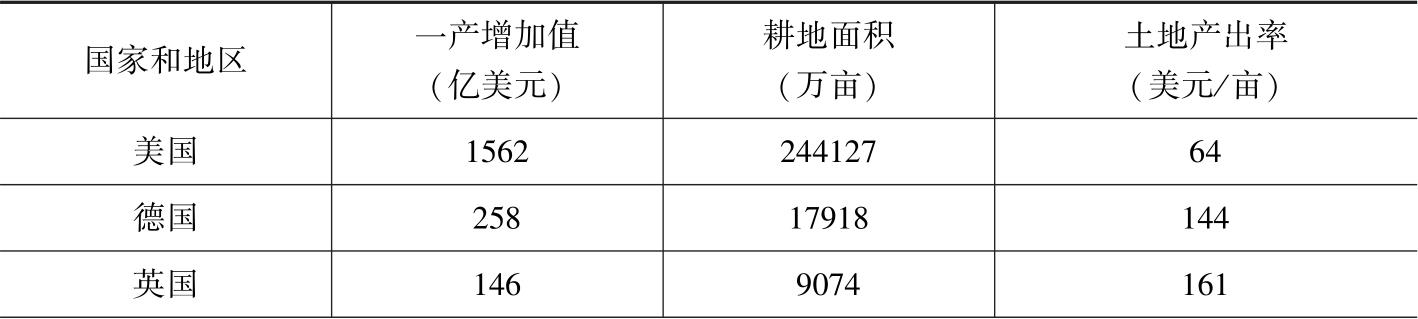
续表
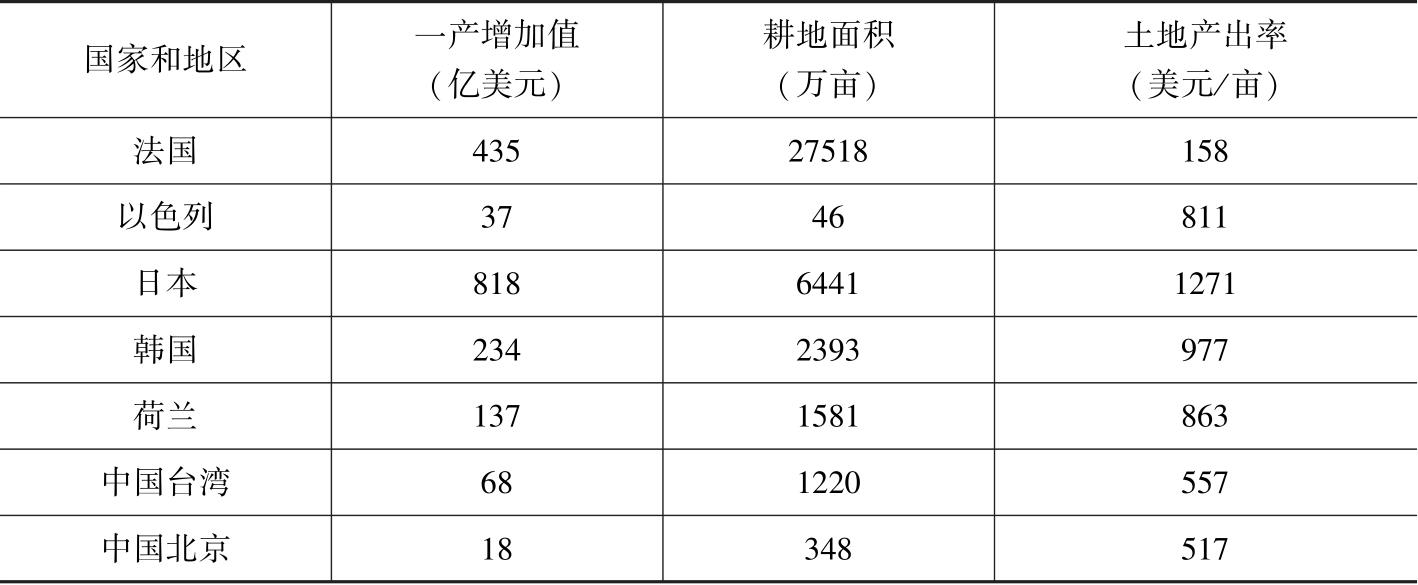
资料来源:依据北京市统计局《北京统计年鉴》、世界银行《世界发展指标》数据库整理。
根据协整理论,若变量间存在协整关系,则可以用误差修正模型描述各变量间的长期均衡与短期波动关系。前面通过协整检验建立起来的北京农业生产功能与各个时间序列之间的长期均衡关系,在受到短期干扰时是否仍然成立,就可以通过在协整关系的基础上建立一个动态的向量误差修正模型进行考察分析。
按照HendryAnderson从一般到特殊的建模技术,去除不太重要的向量EC、NFT和FAA,得到LNALP与LNPPCGDP、LNDPI、LNRD的向量误差修正模型VECM如下:
△LNALP t =△LNGDP t (-1)-2.74△LNDPI t (-1)+3.299△LNRD t (-1)-2.68VECM t
根据误差修正理论,误差修正模型各差分变量的系数反映了短期变动的影响,误差修正项VCEM为负,表明误差修正项对△LNALPt的控制为一个负反馈过程。
变量之间回归分析考虑的是一个变量依赖于另一个变量,变量间的这种关系的存在不能够证明是因果关系或者影响的方向。Grange因果关系检验中Y i 是Y j 的原因,指的是除了这个系统中其他变量的影响之外,Y i 包含着可预见Y j 的有用的信息。
为了确定农业多功能演进与人均GDP、居民家庭可支配收入、R&D经费支出之间是否存在长期因果关系,本研究采用Grange因果关系检验进一步验证。Grange因果检验一般都是以变量相互不具有因果关系为原假设,这样的原假设下主要看P值,P值小于0.05说明具有因果关系。利用Eviews软件中的Grange模型对变量进行因果关系检验,滞后期选择3个,检验结果见表2-12。
表2-12 Grange因果关系检验结果
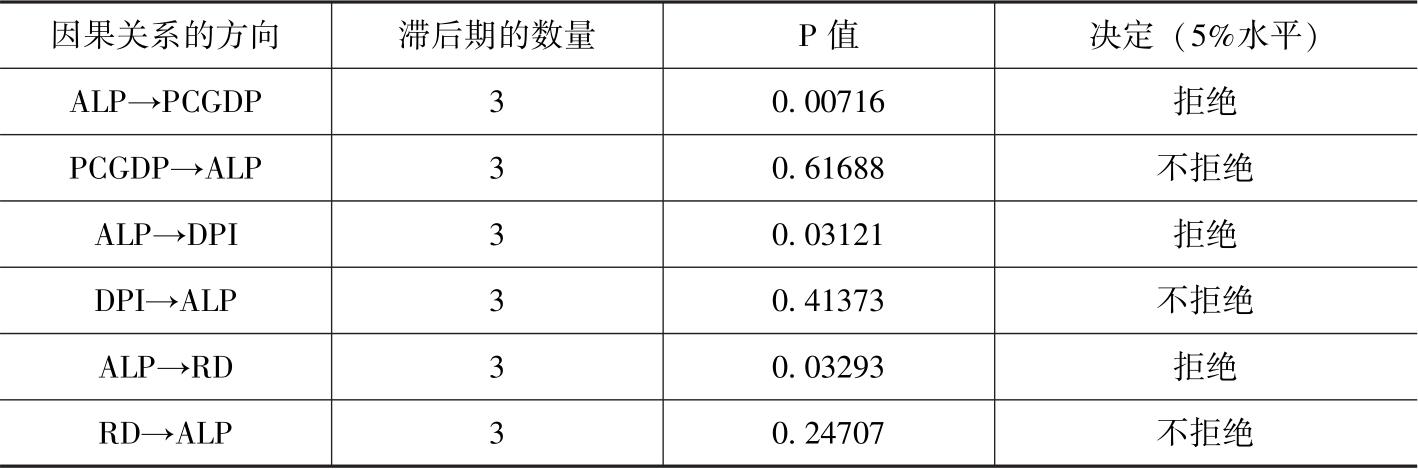
Grange因果关系检验结果显示,存在从人均GDP(PCGDP)、城镇居民人均可支配收入(DPI)、农业R&D经费支出占一产增加值比重(RD)到北京农业生产功能演进的单向Grange因果关系。即人均GDP、城镇居民人均可支配收入、农业R&D支出比重是北京农业生产功能演进的Grange原因。