下载掌阅APP，畅读海量书库
立即打开
逻辑代数式是逻辑运算关系的代数符号表示式。上节中所给出的表示逻辑关系的式子即逻辑代数式。基本逻辑运算关系的逻辑代数式如下。
“与”运算 ：F = A·B
“或”运算 ：F = A + B
“非”运算 ：F =
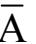
对于“与”“或”运算的表示，“·”和“+”已得到普遍认可，对此不再有其他异议。但对于“非”运算，不同的资料书籍中表示不相同，除了采用
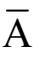外，也有采用~A,A’等，但采用
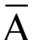较多。“
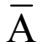”读作“A非”或“A反”均可。
逻辑代数式是逻辑函数的一种表示方法。在逻辑代数式中，F表示逻辑函数的因变量，而A、B表示逻辑函数的自变量，统称为逻辑变量。与普通代数变量不同，逻辑变量只有两种取值，“0”和“1”。这里的“0”和“1”表示两种逻辑关系。例如开关的通为 1，断为0；电机的转为 1，停为 0。与普通的代数函数一样，逻辑自变量的值确定后，其因变量必定有一个唯一的值被确定。
逻辑代数非常方便地在继电控制电路和梯形图上得到应用。
PLC的输入端口均为开关量端口，而其输出端口也是开关量端口。通常，输出端口（又称驱动输出）的状态是受输入端口的状态（又称驱动条件）所控制的，而它们之间的关系则完全可以用逻辑代数式来表示。
【 例 1.1-21 】 如图 1.1-6 所示的梯形图，请写出输出Y0 与输入X0，X1 和X2 的逻辑代数表达式。
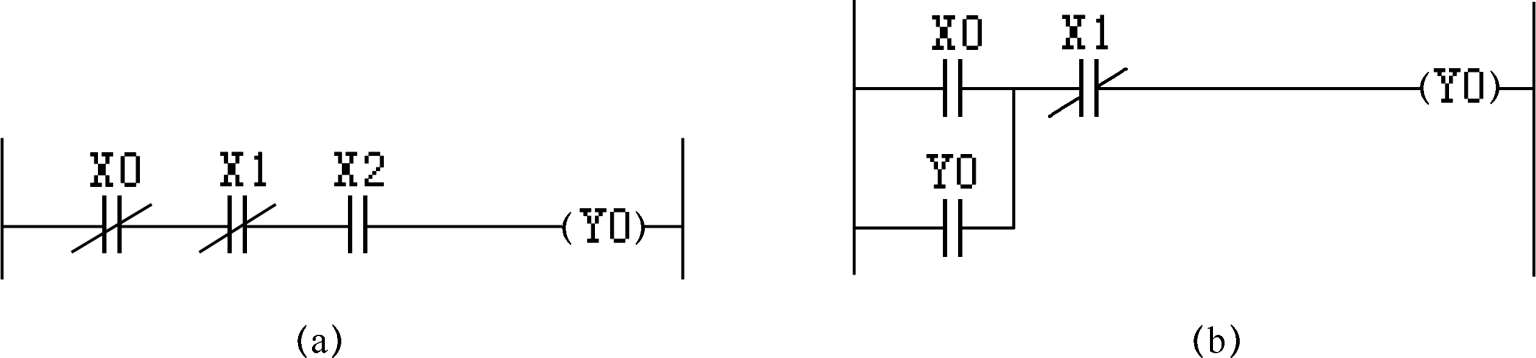
图 1.1-6 梯形图逻辑关系示意图
根据表 1.1-12 的对应关系，很容易写出Y0 与X0，X1，X2 的逻辑代数式。
（a）：Y0 =
·
·
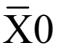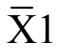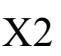
（b）：Y0 = (X0+Y0)·
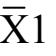
根据逻辑代数式，很容易分析出各种不同的输入状态情况下，输出Y0 的状态。例如，对图（a）来说，仅当X0=0，X1=0，X2=1 时，Y0 才有输出（接通）。X0=X1=0，表示这两个端口是断开的；X2=1，表示其端口是接通的。也就是说，仅当X0，X1 端口断开且X2 端口接通，Y0 才接通。
图 1.1-6 所示的两种逻辑关系也代表了逻辑控制关系的两大类型。
图（a）的输出Y0 的状态仅与输入的当前状态有关，而与输入输出的以前状态无关。这种逻辑控制关系称作组合逻辑控制。
图（b）的输出Y0 的状态不但与输入的当前状态有关，还和输入输出的过去状态有关。在其逻辑代数式中，不但有输入逻辑变量，还有输出逻辑变量，如式中的（X0+Y0）。这种表达式中含有输出逻辑变量的逻辑控制关系称作时序逻辑控制。
在实际应用中，组合逻辑控制可以直接应用逻辑代数的基本知识，易学易掌握，在梯形图的设计中有一定的方法和步骤。而时序逻辑控制到目前为止仍然没有易学易掌握的方法和步骤。关于这两种逻辑控制的更多知识，读者可参看数字电子技术相关书籍和资料。
下面举例说明组合逻辑控制在梯形图设计中的应用。
【 例 1.1-22 】 两地控制一盏灯，控制要求是：灯灭时任一处拨动一次开关，灯亮；灯亮时，任一处拨动一次开关，灯灭。
解： 设逻辑动作为：开关向下拨为 0，向上拨为 1，灯亮为 1，灯灭为 0。开关不拨动，维持原状。
根据题意可列出其逻辑关系见表 1.1-13。
表 1.1-13 逻辑关系
根据表 1.1-13.可知，仅处理灯亮时的逻辑关系。则灯亮与开关X1，开关X2 之间的逻辑关系式是
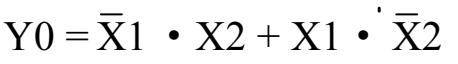
所设计的梯形图如图 1.1-7 所示。
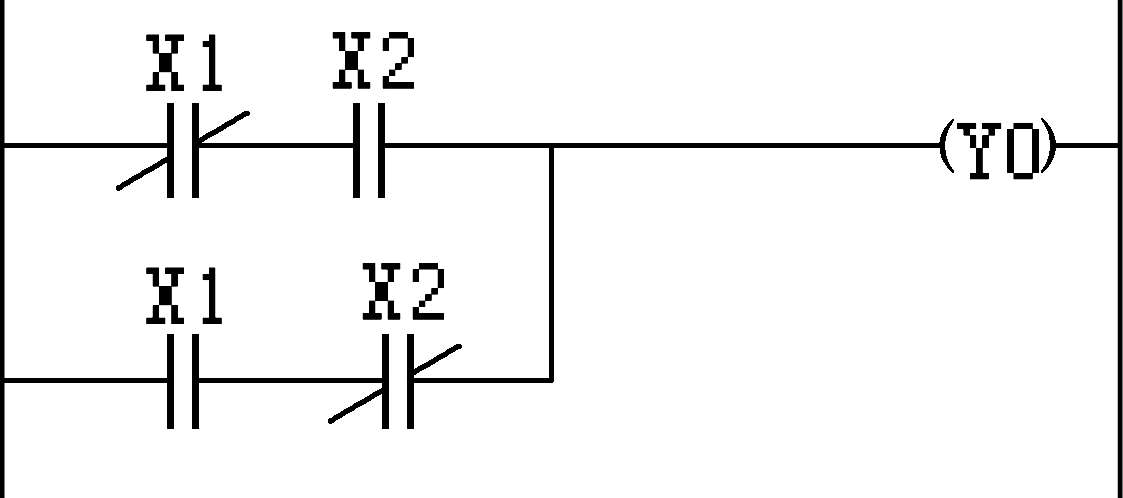
图 1.1-7 例 22 梯形图
【试试，你行的】
（1）在逻辑代数中，所有变量取值的特点是什么？
（2）试说明三种基本逻辑运算的运算口诀。
（3）试写出图P1-1 所示梯形图的逻辑关系表达式。
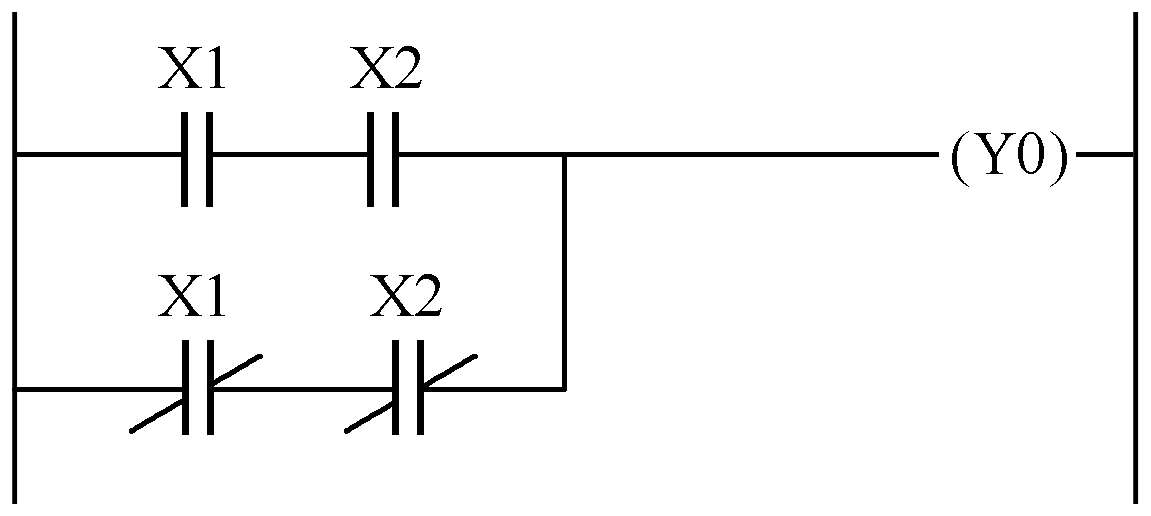
图P1-1
（4）三个地方A，B，C有三个开关，同时控制一盏灯，控制要求是：如果灯是灭的，则按任何一个开关均可将其打开：如果灯是亮的，则按任何一个开关均可将其关闭。试设计梯形图程序。