




在工程上的许多问题中,统计数据往往满足正态分布规律。正态分布简单,参量少,分析方便,是一种适宜的数学模型。
尽管不同的人手写数字形状有所区别,但在特征空间中对某一类的特征进行观察时,这些手写的数字较多地分布在这一类的均值附近,远离均值点较少,因此用正态分布作为这一类的概率模型是合理的。
要想了解手写数字特征空间分布情况,需要根据现有的训练样本集,对总体参数做点估计和区间估计,然后假设样本的总体分布函数,对总体分布函数进行统计假设检验。由于对手写数字提取了25维特征,为了简化分布分析过程,对手写数字特征空间水平投影降维为5维。在此基础上进行主成分分析,提取第一主成分分量作为有效特征,进行一维正态分布分析。
(1)总体参数的点估计
采用最大似然法对手写数字总体参数进行点估计。
由于假设手写数字特征分布遵从正态分布 N ( μ , σ 2 ),但总体参数 θ ( μ , σ 2 )未知,对于正态总体的参数估计现在要用总体的 N 次观测值 x 1 , x 2 ,…, x N ,求 μ , σ 2 的最大似然估值。
一元总体的分布密度函数为

似然函数为
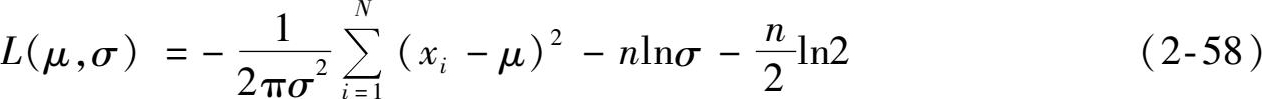
解方程组
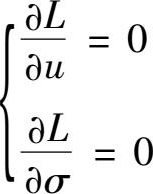
得
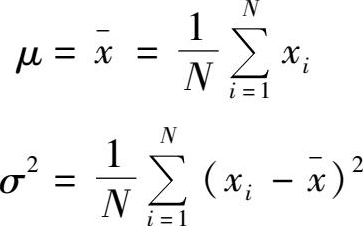
容易检验 μ , σ 2 确实使 L ( μ , σ )取到最大值,因此它们分别是 μ , σ 2 的最大似然估值。
(2)估值好坏的判别标准
①无偏性。如果参数
θ
的估值
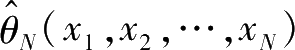 满足关系式
满足关系式
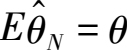
则称
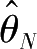 是
θ
的无偏估值。
是
θ
的无偏估值。
②有效性。如果
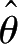 和
和
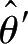 都是参数
θ
的无偏估值
都是参数
θ
的无偏估值
则称
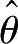 比
比
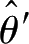 有效。进一步,如果固定样本的容量
N
,使
有效。进一步,如果固定样本的容量
N
,使
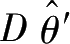 =极小值的无偏估值
=极小值的无偏估值
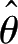 就成为
θ
的有效估值。
就成为
θ
的有效估值。
③一致性。如果对任意给定的正数 ε ,总有
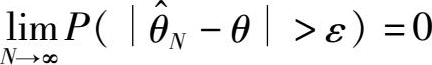
则称
θ
的估值
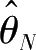 是一致的。当
是一致的。当
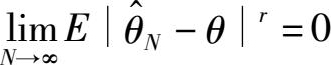
对某
r
≥0成立时,
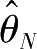 是
θ
的一致估值。
是
θ
的一致估值。
(3)总体参数的区间估计
在一次试验中,概率很小(接近于零)的事件认为是实际上不可能发生的事件;而概率接近于1的事件认为是实际上必然发生的事件。
对总体参数 θ ( μ , σ 2 )进行区间估计(即区间参数的取值范围)时,如果对于预先给定的很小的概率 α ,能找到一个区间( θ 1 , θ 2 ),使得
那么称区间( θ 1 , θ 2 )为参数 θ 的置信区间, θ 1 和 θ 2 称为置信限(或临界值); θ ≤ θ 1 和 θ ≥ θ 2 称为否定域;概率 α 称为显著性水平,1- α 称为置信水平(或置信概率)。
假设总体遵从正态分布 N ( μ , σ 2 )。对于预先给定的显著性水平 α ,可用一个样本{ x 1 , x 2 ,…, x N }的均值 x 和标准差 s 来估计总体的均值 μ 和方差 σ 2 的置信区间,估计方法如表2‐2所示。
表2‐2 (小样本)置信区间的估计方法

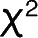 检验法
检验法
(1)
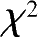 检验法
检验法
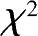 检验法是基于对数据按其取值范围进行分组后计算频数的基础上,考虑每个区间的实际频数{
v
i
}与理论频数{
p
i
}的差异做出判断。它使用的统计量
检验法是基于对数据按其取值范围进行分组后计算频数的基础上,考虑每个区间的实际频数{
v
i
}与理论频数{
p
i
}的差异做出判断。它使用的统计量

其中, N 为样本数据的容量, l 是分组数, p i 根据原假设指定的分布求得。
(2)检验步骤
假设 x 的分布函数为 F ( x ),这时,相应的假设检验问题为
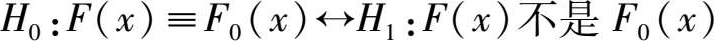
分两种情况进行统计假设检验。
①设 F 0 ( x )= F 0 ( x , θ 1 , θ 2 ,…, θ k )为已知类型的分布函数, θ 1 , θ 2 ,…, θ k 为参数(已知或部分已知), x 1 , x 2 ,…, x N 为总体 X 的样本,把实轴(-∞,∞)分成 l 个不相交的区间:( c i , c i +1]( i =1,2,…, l ), c 1 =-∞, c l +1=∞,其中( c l , c l +1]理解成( c l ,∞)。
理论频数记为
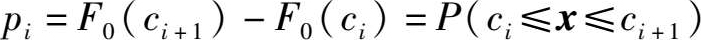
x
的样本{
x
1
,
x
2
,…,
x
N
}落在区间(
c
i
,
c
i
+1]的个数为
v
i
(经验频数),根据式(2‐59)计算统计量
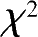 。设
k
是原假设指定的分布类中的待估参数的个数,遵从自由度为
l
-
k
-1的
。设
k
是原假设指定的分布类中的待估参数的个数,遵从自由度为
l
-
k
-1的
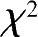 分布,应用
分布,应用
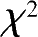 检验法便可检验假设
H
0
:
F
(
x
)=
F
0
(
x
)是否可信。
检验法便可检验假设
H
0
:
F
(
x
)=
F
0
(
x
)是否可信。
若原假设成立,
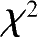 的值应比较小,所以当
的值应比较小,所以当
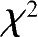 取大的值时是极端情形。
取大的值时是极端情形。
例如,原假设是正态分布,
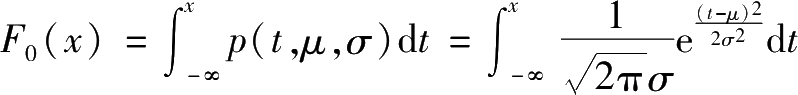 ,此时
k=
2,统计学研究表明:当样本容量
N
充分大且原假设
H
0
为真时,
,此时
k=
2,统计学研究表明:当样本容量
N
充分大且原假设
H
0
为真时,
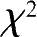 统计量近似服从自由度为
l-k-
1的
统计量近似服从自由度为
l-k-
1的
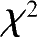 分布,即
分布,即
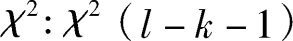
给定显著水平
α
,设由样本观测值算得的
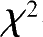 值是
值是
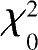 。则当
。则当
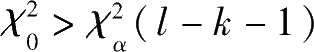 时,拒绝
H
0
;否则,接受
H
0
。
时,拒绝
H
0
;否则,接受
H
0
。
②
F
0
(
x
)的参数全部或一部分未知。设
F
0
(
x
)有
l
个参数
θ
j
1,
θ
j
2,…,
θ
jl
(
j
≤
k
)未知,可先用最大似然估计法定出这
l
个参数的估值,把这些估值就当做
F
0
(
x
)的相应参数,于是类似①的情形可计算理论概率,再计算经验频数,那么按式(2‐59)计算统计量。当
N
很大时遵从自由度为
l
-
k
-1的
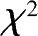 分布。
分布。
应用
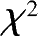 检验法便可检验假设:
H
0
:
F
(
x
)=
F
0
(
x
)是否可行。
检验法便可检验假设:
H
0
:
F
(
x
)=
F
0
(
x
)是否可行。
由于对手写数字用模板法提取了25个特征,每种数字样本库总数约为130个,造成特征维数多,样品总数少的情况。为了分析样本的空间分布情况,采用行投影法将25个特征压缩为5个,进一步采用主成分分析法,取特征值最大的主分量作为每个样品的特征,进行正态分布检验,实现步骤如下。
①选取样本库中的某一类全体样本 X n×N 。
②对25个特征做行投影变换,压缩为5个特征。
③用主成分分析法选取特征第一主成分。
 计算
X
的协方差矩阵
S
n×
n
。
计算
X
的协方差矩阵
S
n×
n
。
 计算
S
的特征值
λ
1
>
λ
2
>…>
λ
n
和相应特征向量
C
n×
n
。
计算
S
的特征值
λ
1
>
λ
2
>…>
λ
n
和相应特征向量
C
n×
n
。
 计算样本库样本的第一个主分量
计算样本库样本的第一个主分量
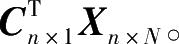
④输出特征分布直方图。
⑤正态分析检验。

数字0特征空间分布检验效果如图2‐8所示。
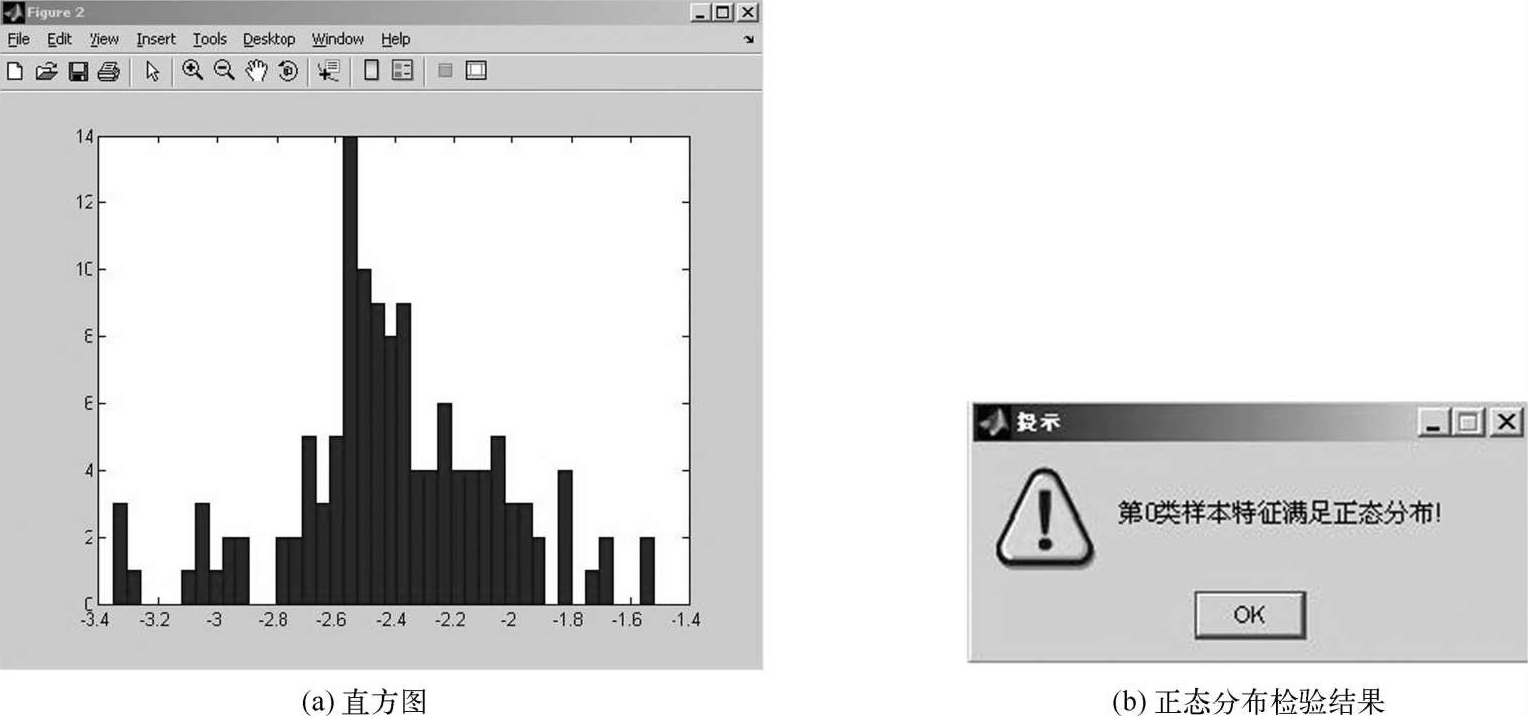
图2‐8 数字0特征空间分布检验效果图