




在讨论了判别函数等概念后,设计分类器的任务就清楚了。根据样品分布情况来确定分类器的类型。在设计分类器的方法时,要有一个样品集,样品集中的样品用一个各分量含义已经确定的向量来描述,也就是说对要分类的样品怎样描述这个问题是已经确定的。在这种条件下研究用贝叶斯分类器、线性分类器与非线性分类器等,以及这些分类器的其他设计问题。
按照基于统计参数的决策分类方法,判别函数及决策面方程的类别确定是由样品分布规律决定的,贝叶斯决策是基于统计分布确定的情况下计算的,如果要按贝叶斯决策方法设计分类器,就必须设法获得必需的统计参数。当有条件得到准确的统计分布知识,具体说来包括各类先验概率
P
(
ω
1
)及类条件概率密度函数,从而可以计算出样品的后验概率
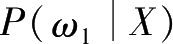 ,并以此作为产生判别函数的必要依据,利用贝叶斯决策来实现对样品的分类。但是,在这些参数未知的情况下使用贝叶斯决策方法,就得有一个学习阶段。在这个阶段,设法获得一定数量的样品,然后从这些样品数据获得对样品概率分布的估计。有了概率分布的估计后,才能对未知的新样品按贝叶斯决策方法实行分类。
,并以此作为产生判别函数的必要依据,利用贝叶斯决策来实现对样品的分类。但是,在这些参数未知的情况下使用贝叶斯决策方法,就得有一个学习阶段。在这个阶段,设法获得一定数量的样品,然后从这些样品数据获得对样品概率分布的估计。有了概率分布的估计后,才能对未知的新样品按贝叶斯决策方法实行分类。
在一般情况下要得到准确的统计分布知识是极其困难的事。当实际问题中并不具备获取准确统计分布的条件时,使用几何分类器。几何分类器设计过程主要是判别函数、决策面方程的确定过程。设计分类器首先要确定准则函数,然后再利用训练样品集确定该分类器的参数,以求使所确定的准则达到最佳。在使用分类器时,样品的分类由其判别函数值决定。判别函数可以是线性函数、也可以设计成非线性函数。设特征向量的特征分量数目为 n ,可分类数目为 M ,符合某种条件就可使用线性分类器,正态分布条件下一般适合用二次函数决策面。
(1)若可分类数目 M =2( n +1)≈2 n ,则几乎无法用一个线性函数分类器将它们分成两类。
(2)在模式识别中,理论上, M > n +1的线性分类器不能应用,但是如果一个类别的特征向量在空间中密集地聚集在一起,几乎不和其他类别的特征向量混合在一起,则无论 M 多大,线性分类器的效果总是良好的。在字符识别机中,线性函数分类器已经证明能够提供良好的识别效果,它能识别数量很大的字符识别任务。
因此,在手写数字识别中,只要读者规范书写数字,不同数字类别的特征空间可以看成彼此分离的,而同一类别的数字在特征空间中集群性质较好,应用线性分类器是可行的。相反,如果特征向量的类集群性质不好,则线性分类器的效果总是不理想,此时,必须求助于非线性分类器。