





粒子群算法是一种源于模拟生物群体捕食行为中相互协作的群体智能算法。假设
n
D
维解空间存在
N
个不同变量
x
=(
x
1
,
x
2
,…,
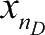 )的粒子,
x
l
=(
x
l1
,
x
l2
,…,
)的粒子,
x
l
=(
x
l1
,
x
l2
,…,
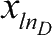 ),第
l
个粒子当前经历过的最优位置为
p
l
=(
p
l1
,
p
l2
,…,
),第
l
个粒子当前经历过的最优位置为
p
l
=(
p
l1
,
p
l2
,…,
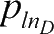 ),第
l
个粒子的速度为
),第
l
个粒子的速度为
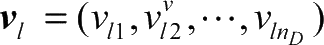 ,种群全局最优粒子为
p
g
=(
p
g1
,
p
g2
,…,
,种群全局最优粒子为
p
g
=(
p
g1
,
p
g2
,…,
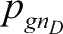 )。在进化过程中,每一代各粒子在本身惯性速度的基础上,同时向当前的粒子自身历史最优位置和群体最优位置方向加速获得新的速度,并对所在位置进行更新。设
k
为粒子进化代数,粒子群优化进化更新算法如下:
)。在进化过程中,每一代各粒子在本身惯性速度的基础上,同时向当前的粒子自身历史最优位置和群体最优位置方向加速获得新的速度,并对所在位置进行更新。设
k
为粒子进化代数,粒子群优化进化更新算法如下:
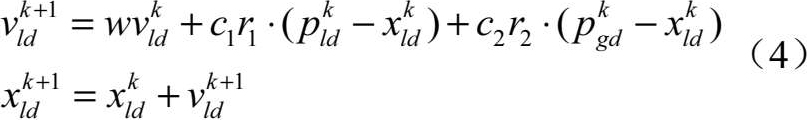
式中,下标 d =1,2,…, n W 代表武器平台变量的维数, r 1 、 r 1 为[0,1]区间均匀分布的随机数, c 1 、 c 1 分别代表粒子自我认知和群体协同能力的加速因子, w 为粒子的惯性权重。
在更新阶段,当粒子速度或位置超界时,对粒子状态进行限定
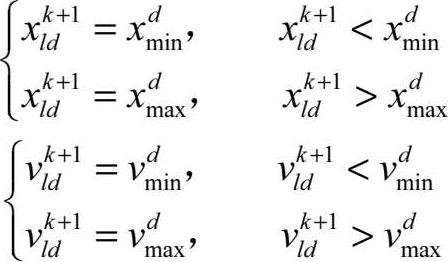
设定粒子群算法总进化代数为 k max ,采用线性递减策略对第 k 代的惯性权重系数进行更新
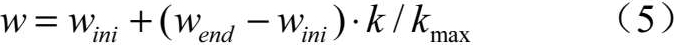
式中, w ini 、 w end 分别为对进化起始代到终止代惯性权重的控制。
火力分配时需要获取整数配对,通常采用对连续粒子群算法的直接离散化方式。算法结构依然保持连续粒子位置和速度更新中的运算规则,而在每次粒子位置更新之后,通过对式(4)中粒子位置进行近似取整运算,并以粒子对应的适应度函数评价此解的质量,然后进行迭代。
用粒子群算法求解火力分配问题时,首先将分配问题进行合理的编码。常规的做法是将粒子对应为长度和火力单元数相同的变量,粒子的每维 x i 表示火力单元拦截的目标编号。这种编码方法概念清晰、编码简单,但求解过程假设每个火力单元都可对任意目标进行拦截,即没有考虑式(3)的作战约束。
一般情况下,用进化算法处理优化问题的约束条件有三种途径:①考虑约束的编码;②引入与约束相关的罚函数;③在进化过程中,检验变量的合法性,迭代生成可行变量。方法②更改了适应度函数,且并没有强制解的合法性;方法③通过反复迭代增加了算法运行时间,当问题维数增大时通常不可取。本文提出了一种新的粒子编码方法,不仅可以保证编码的合法性,而且缩小了解空间的大小,提高了火力分配的优化效率。
约束条件(3)表明了分配需满足一定射击条件:敌来袭目标在武器射程范围内、发射处于就绪状态、未分配射击任务且架上有武器的火力单元。假设经过拦截适应性检验后,
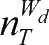 为第
d
个火力单元对应可拦截目标的总数量,第
d
个火力单元可拦截的目标集合,记为拦截可行域为
为第
d
个火力单元对应可拦截目标的总数量,第
d
个火力单元可拦截的目标集合,记为拦截可行域为
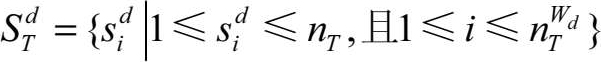
显然,有1≤
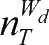 ≤
n
T
,
≤
n
T
,
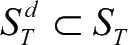 ,即拦截可行域是来袭目标集合的一个子集。
,即拦截可行域是来袭目标集合的一个子集。
设
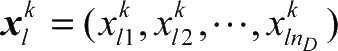 为第
k
代中,第
d
个粒子的
n
D
维位置矢量,粒子第
d
维变量表示第
d
个火力单元与其拦截可行域的第
为第
k
代中,第
d
个粒子的
n
D
维位置矢量,粒子第
d
维变量表示第
d
个火力单元与其拦截可行域的第
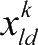 个目标配对,
个目标配对,
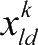 取值范围不能超过第
i
个火力单元拦截可行域的目标数量。采用基于火力单元拦截可行域的粒子编码,可有效缩小防空火力优化问题的映射空间,加速了算法寻优速度。
取值范围不能超过第
i
个火力单元拦截可行域的目标数量。采用基于火力单元拦截可行域的粒子编码,可有效缩小防空火力优化问题的映射空间,加速了算法寻优速度。
进一步地,若
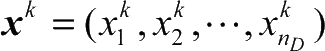 为分配问题的解,则第
d
个武器平台分配拦截的目标为
为分配问题的解,则第
d
个武器平台分配拦截的目标为
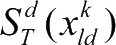 。变量取值范围
。变量取值范围
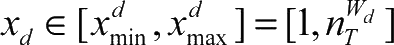 ,同时限定该粒子的飞行速度
v
d
∈
,同时限定该粒子的飞行速度
v
d
∈
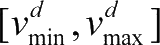 =
=
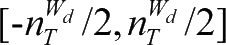 ,粒子各维的速度取值范围反映了对搜索空间的拓展能力。
,粒子各维的速度取值范围反映了对搜索空间的拓展能力。
考虑拦截可行域同粒子编码如图2所示。
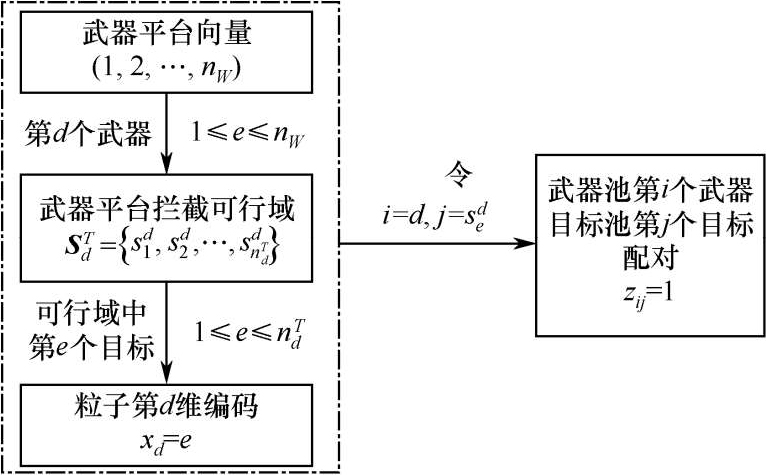
图2考虑拦截可行域的粒子编码
基本的粒子群算法的式(4)表明:粒子的样本在自身最优解和全局最优解的信息引导下,一直处于收缩过程。当找到问题的一个局部最优解时,粒子群将呈现聚集在较小的区域内,适应度函数也趋于停滞更新状态。本质上,粒子群算法在进化过程中,不断降低群体的多样性,也减小了寻优的搜索空间。
为增强群体的多样性,控制算法的搜索过程,首先给出了群体多样性的度量公式:
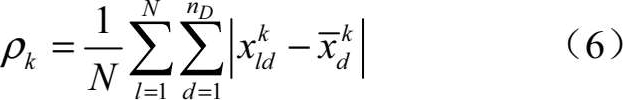
式中,
N
为种群的大小,
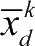 为粒子群第
d
维变量的平均值
为粒子群第
d
维变量的平均值
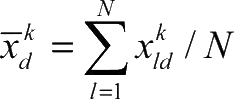 。
。
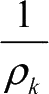 可理解为第
k
代群体的样本浓度,总的群体数量不变,搜索空间越大,样本浓度越低。
可理解为第
k
代群体的样本浓度,总的群体数量不变,搜索空间越大,样本浓度越低。
当粒子群的多样性 ρ k 小于 ρ min 时,粒子就开始向中心的反向加速,采用如下速度更新策略:
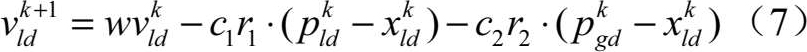
粒子群的多样性满足 ρ k 大于 ρ min 时,粒子停止发散运动,采用式(4)更新策略开始向着中心收缩。该修正策略从效果上看如同粒子间存在一个斥力,当间距小于允许值时,该斥力便产生作用,将各粒子推至斥力影响范围之外。粒子群在多样性的指导下反复作收缩与发散运动,可以在群体聚集时呈现增大样本空间的趋势,跳出局部最优情形。