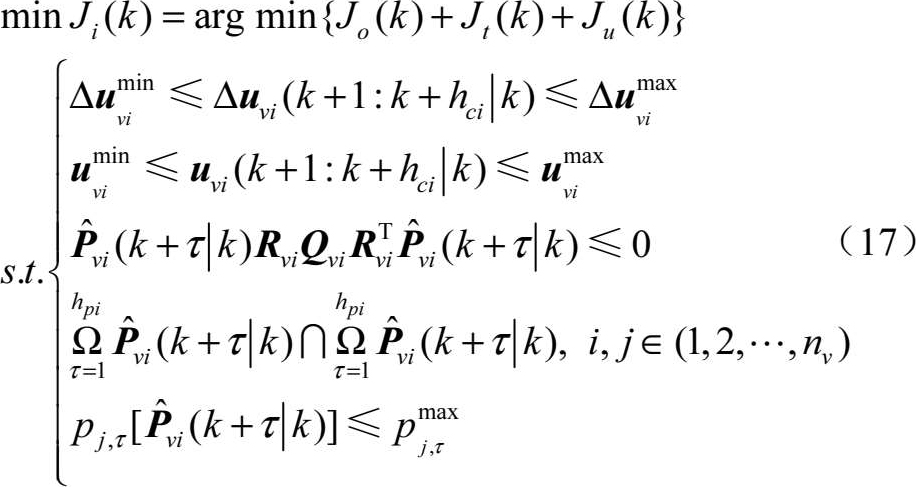2基于模型预测控制的多无人机协同防碰撞算法

根据无人机六自由度运动方程组 ^[13] ，令多无人机编队内部每一个成员在地理坐标系中三个轴向的分速度分别为 ， ， ：

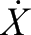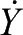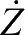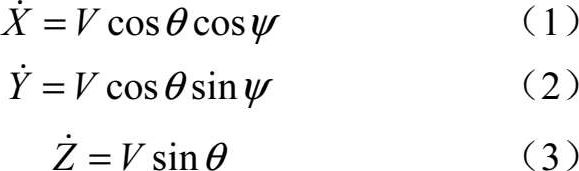
式中， X ， Y ， Z 分别为无人机的三轴坐标， ψ ， θ 分别为无人机的航迹偏角和航迹倾角， V 为无人机的飞行速度标量。

离散后的无人机运动模型为

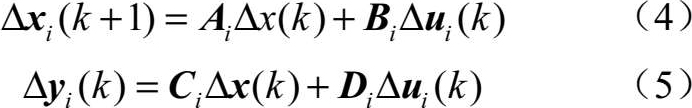
式中， k 为当前采样时刻， x _i ( k )为第 i 架无人机的状态矢量， y _i ( k )为输出矢量， A ， B ， C ， D 为状态方程的相应矩阵。Δ u _i ( k )=[Δ u _vi ( k ), Δ u _ψi ( k ),Δ u _zi ( k )] ^T 分别为速度、偏航和高度的控制指令矢量。

令 h _pi 表示整数预测时域， τ ∈[1, h _pi ]，采用扩展卡尔曼滤波算法得到的障碍物、目标点以及无人机的预测轨迹分别为

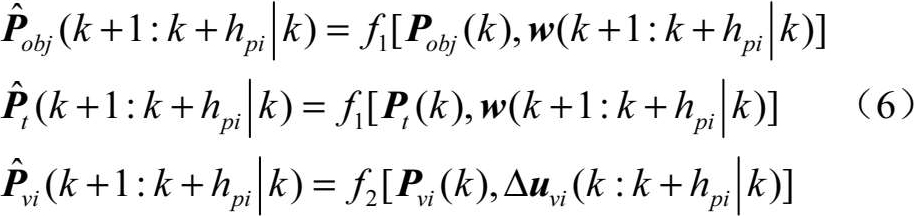
式中，Δ u _vi ( k : k + h _pi | k )=[Δ u _vi ( k ),Δ u _vi ( k +1),…,Δ u _vi ( k + h _pi )] ^T, ， w ( k +1: k + h _pi | k )为障碍物或目标点对应的输入。

为完成防碰撞，将性能指标函数设置如下。

2.1与障碍物防碰撞

定义如下高斯密度函数：

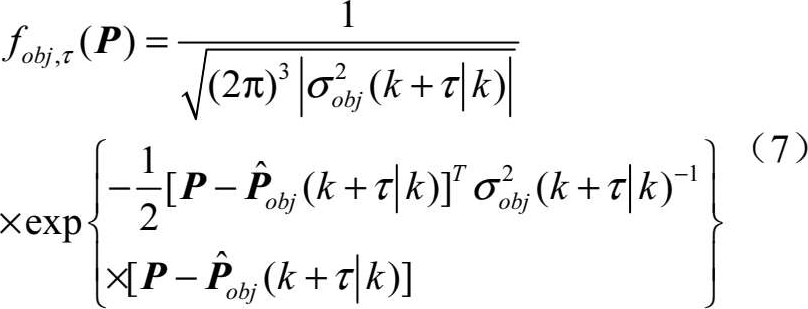
式中， P =[ x , y , z ]为任意位置坐标。

则点 P 落在第 j 个障碍物中的概率为

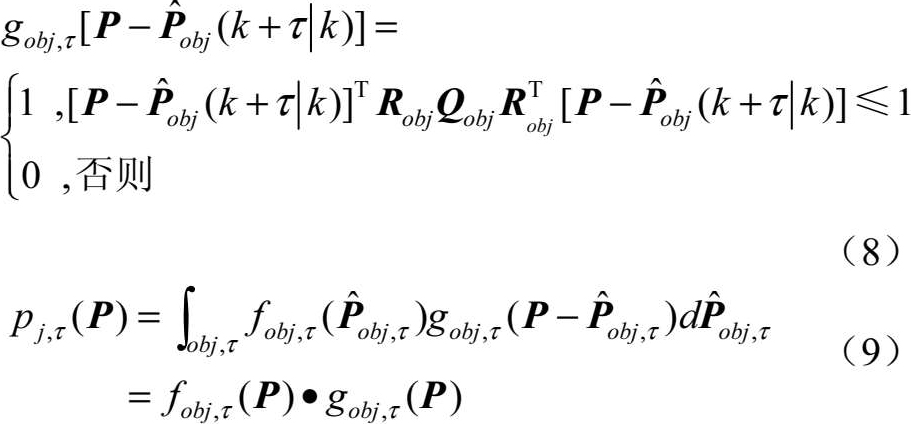
式中， R _obj ， Q _obj 分别表示障碍物的三轴尺寸和欧拉角。

J _O ( k )由无人机与被感知的障碍物在 h _pi 时间内的碰撞概率来描述。

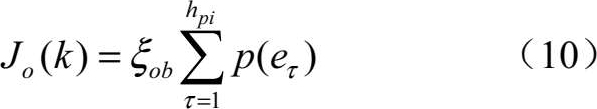
式中， ξ _ob 为权衡常数， e _τ 表示在预测时刻 k + τ 发生碰撞事件，

2.2靠近目标

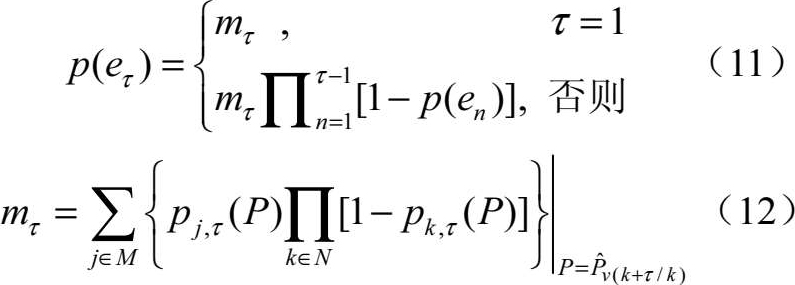
为确保无人机编队尽快完成任务，必须使无人机在尽量短的时间内到达目标点位置，令

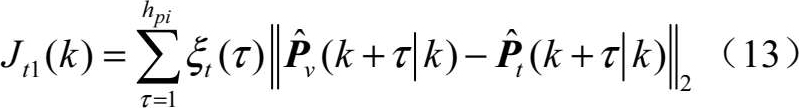
式中， ξ _t ( τ )为权衡常数。

为提高任务完成效率，应尽量同时到达。令

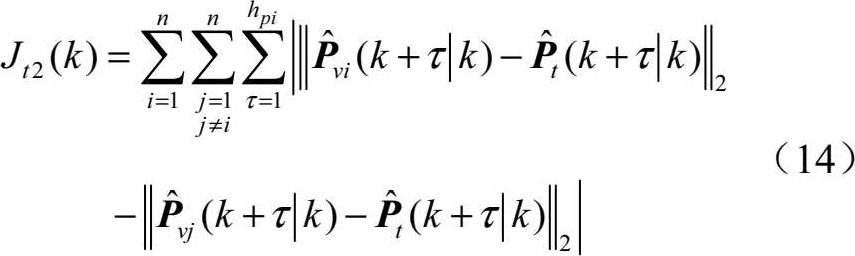
则 J _t ( k )可以表示为

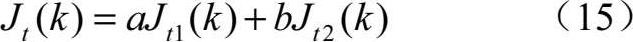
式中， a , b 分别为权衡常数。

2.3惩罚控制输入

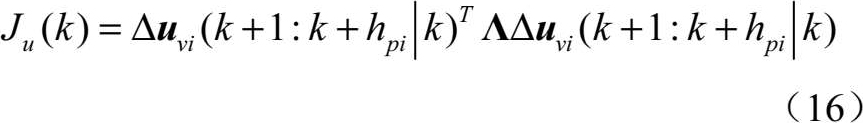
式中， Λ 为一个3 h _pi × 3 h _pi 的对角矩阵，表示自动驾驶仪控制指令输入增量的权重。

根据无人机本身动态约束条件、机间防碰撞约束以及性能指标，无人机协同防碰撞问题描述如下，采用模型预测滚动优化进行求解。 Mwnq5MEH9zcbHN4NzgXKVyxpkggW/HGAjfNJBsBk4msgc/Y6faz1MrXyaIBdmlwP