





UCAV远距空战占位航迹规划分为两段执行:第一段为UCAV规避目标的探测与攻击威胁;第二段为UCAV以低可见性(低RCS)接近目标,达到攻击条件后发射导弹进行攻击。航迹规划流程如图1所示。
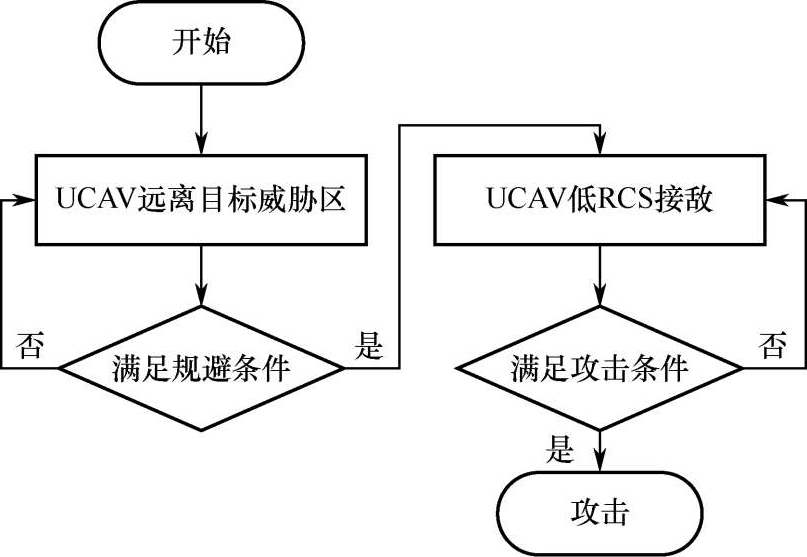
图1攻击占位流程图
1.1.1 UCAV三自由度模型
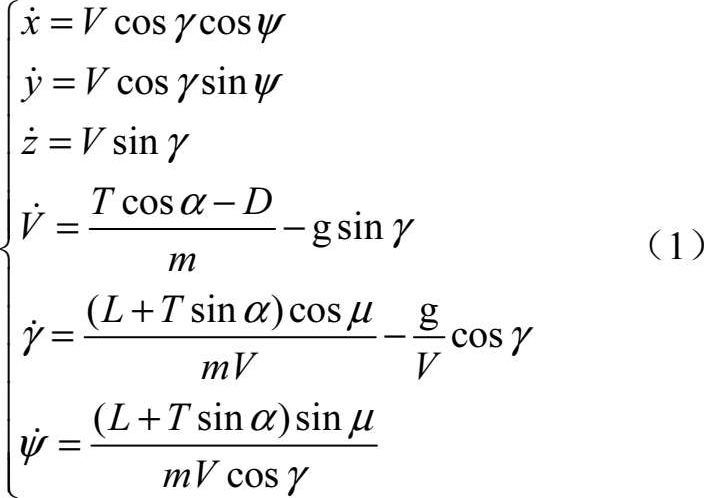
其中,

式中,
x
、
y
、
z
为UCAV在惯性坐标系下的坐标;
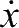 、
、
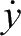 、
、
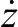 分别为UCAV在各轴上的速度分量;
V
为UCAV速度标量;
γ
、
ψ
、
μ
、
α
分别为UCAV航迹倾角、航迹偏角、滚转角和迎角;
L
、
T
max
、
T
、
D
分别为UCAV的升力、极限推力、实际推力和阻力;
δ
表示油门;g为重力加速度。
分别为UCAV在各轴上的速度分量;
V
为UCAV速度标量;
γ
、
ψ
、
μ
、
α
分别为UCAV航迹倾角、航迹偏角、滚转角和迎角;
L
、
T
max
、
T
、
D
分别为UCAV的升力、极限推力、实际推力和阻力;
δ
表示油门;g为重力加速度。
1.1.2导弹攻击区模型
针对远距空战,只考虑导弹攻击区远边界的影响,采用黄金分割法 [7] 求得目标高度在7000m的条件下导弹攻击区远边界,如图2所示。
然而实际空战中,导弹发射存在离轴角(视线与速度矢量夹角),考虑水平离轴角对攻击区远边界的影响,假定离轴角最大范围±45°,给出360°全向攻击区远边界与水平离轴角的关系,如图3所示。
已知目标状态,结合UCAV自身状态便可通过插值得到当前导弹最大攻击距离。
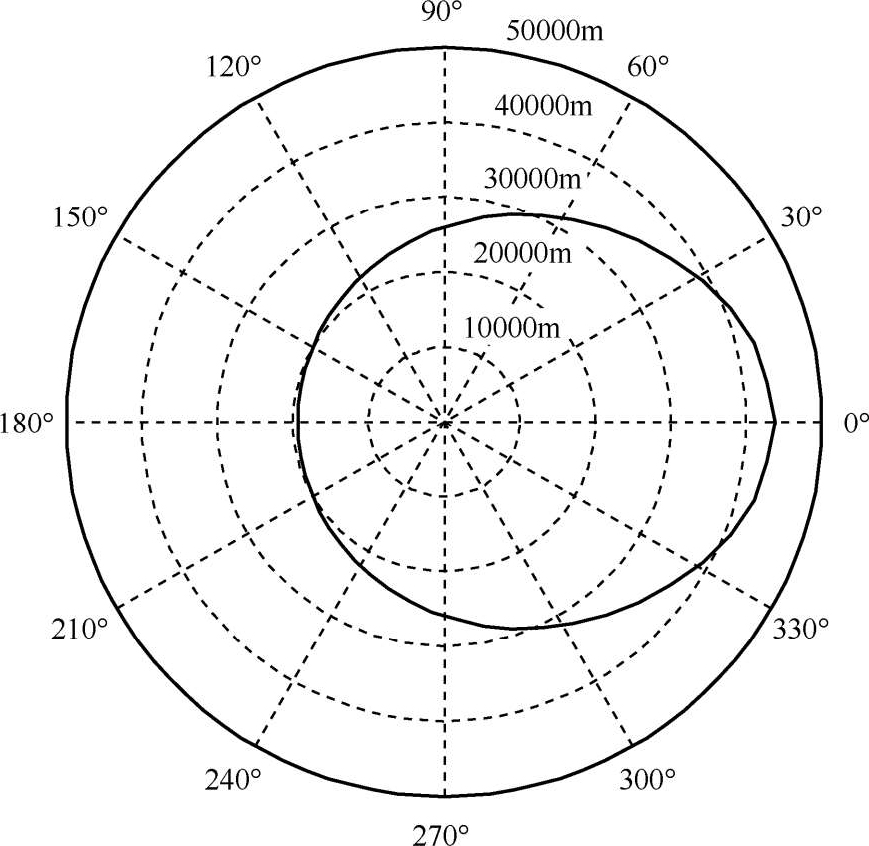
图2导弹攻击区远边界
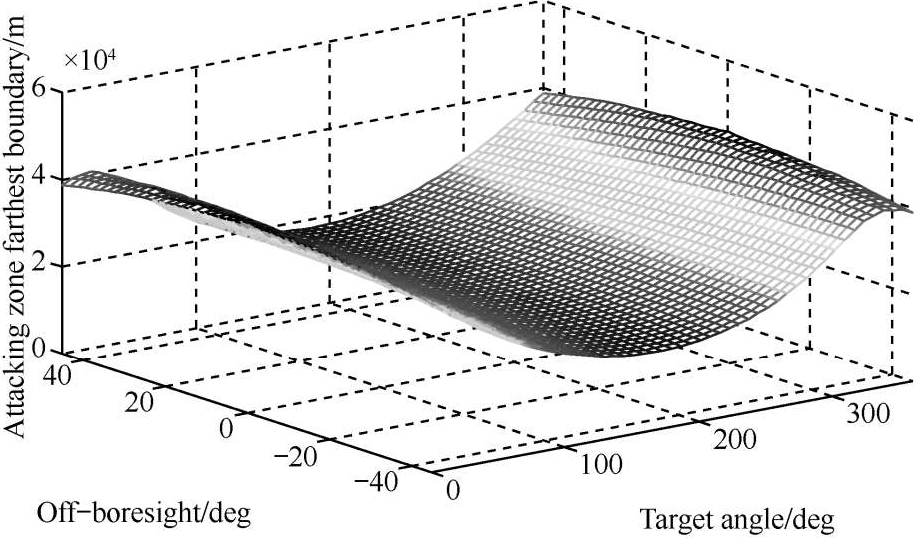
图3水平离轴角与攻击区远边界插值
1.1.3椭球体RCS模型
由于一般飞行器前向和尾向回波面积较小,两翼方向较大,俯仰方向回波面积最大,采用文献[8]提出的简易椭球体RCS模型:
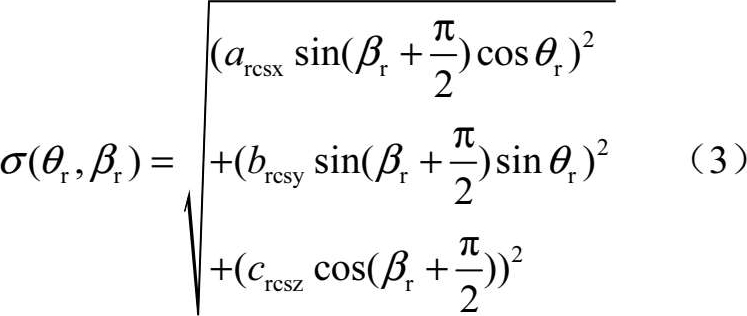
式中, θ r , β r 分别为雷达观测的方位角和仰角;a rcsx 、b rcsy 、c rcsz 分别为机体轴向、两翼和腹背方向RCS值。在此,假设三者分别为1m 2 、5m 2 、10m 2 ,UCAV全向RCS如图4所示。
根据雷达方程 [9] 可得无人机RCS与最大探测距离的四次方成线性关系。
设 R max 对应的RCS为 σ 0 ,某时刻目标相对UCAV距离为 R ,相对目标视线方向的RCS值为 σ ,则UCAV可探测距离表达式为
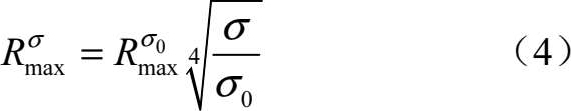
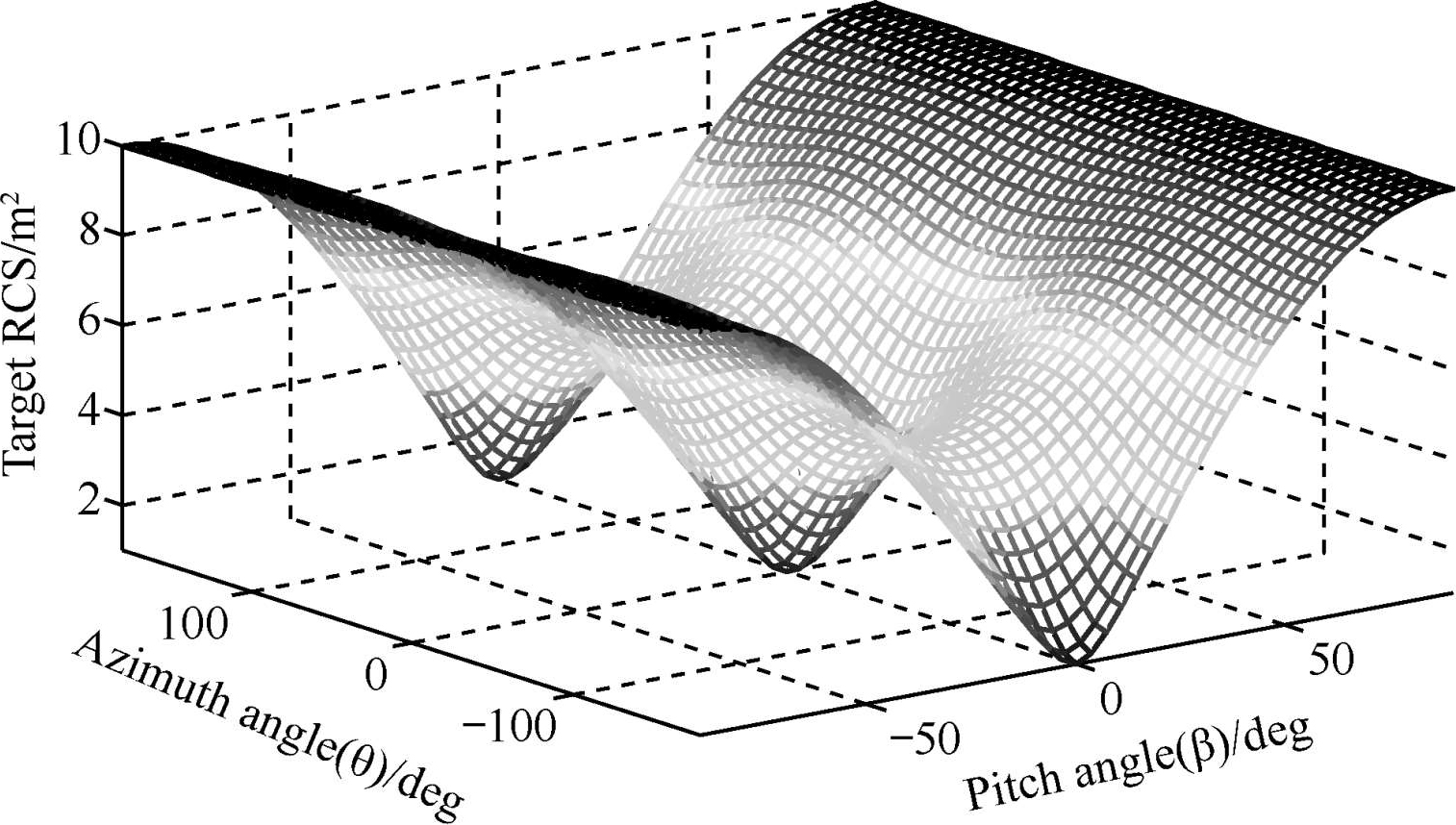
图4 UCAV全向RCS
若
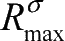 ≥
R
,则UCAV可以被探测到。
≥
R
,则UCAV可以被探测到。
UCAV远距空战攻击是在已知目标运动状态下,通过调整UCAV速度、角度等参数,规避敌机探测威胁和火力威胁,使UCAV自身位于目标的可探测范围外,同时使目标位于UCAV雷达可探测区与导弹可攻击区的交集内,如图5所示。
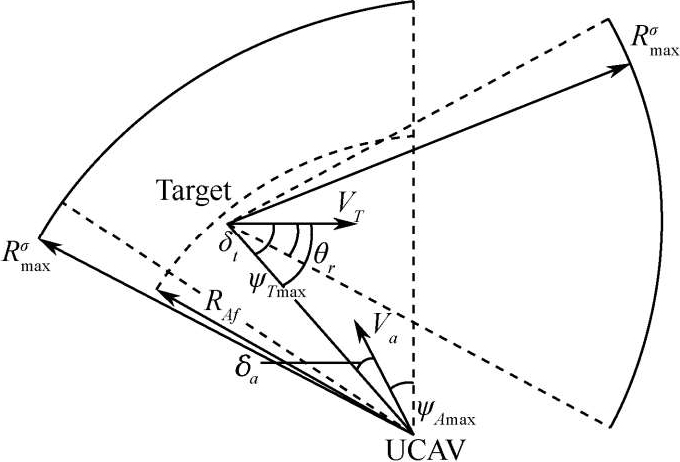
图5 UCAV远距攻击占位示意图
UCAV可在水平面内或是俯仰平面内规避目标探测威胁。本文选择在所需机动较小的水平面内进行规避,所以决定火控雷达性能的主要指标也即需要考虑的威胁要素有:最大搜索方位角
ψ
max
、最大扫描、跟踪距离
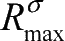 和UCAV相对目标方位角
θ
r
。
和UCAV相对目标方位角
θ
r
。
假设导弹最大发射离轴角与雷达最大探测角度相同,因此选用决定导弹性能的威胁要素有:最大攻击距离 R Af 。
1.2.1目标威胁规避评价指标
目标威胁规避主要以UCAV相对目标方位角
θ
r
、最大搜索方位角
ψ
max
和最大扫描、跟踪距离
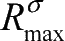 为衡量标准。规避目的是使UCAV不在目标探测范围内。
为衡量标准。规避目的是使UCAV不在目标探测范围内。
(1)| ψ Tmax |≤ θ r :当相对目标方位角大于目标雷达最大水平探测角时,UCAV位于目标探测视场角包络范围外;函数取最优。
(2)0≤| θ r |< ψ Tmax :当相对目标方位角小于目标雷达最大水平探测角时,UCAV位于目标探测包络范围内;函数取值随| θ r |增大而增大。
基于上述二点,构建目标威胁规避评价指标为
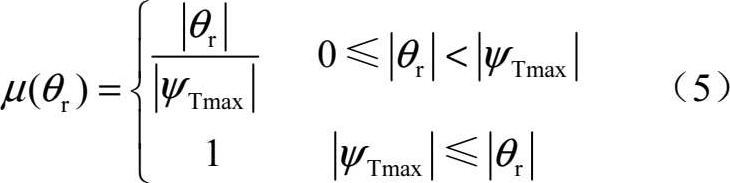
μ ( θ r )越大对UCAV越有利。在此,将1减去 μ ( θ r )的函数值作为UCAV当前时刻的暴露威胁值,即
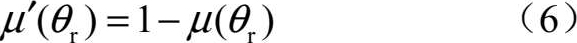
1.2.2 UCAV低可见接敌评价指标
当UCAV位于目标威胁区外时,以低RCS接近目标。目标相对UCAV方位角越大,RCS值越大;当UCAV迎头飞向目标时,UCAV对目标的RCS值最小。
为了能够击毁目标,在目标进入UCAV攻击区域前,UCAV要先使目标在自身雷达的探测区域内,进而让目标在导弹攻击区域内。当UCAV速度矢量与视线夹角 δ a 小于UCAV最大雷达视场角 ψ Amax 时,目标位于UCAV雷达探测范围内。因此,可以构建评价指标为
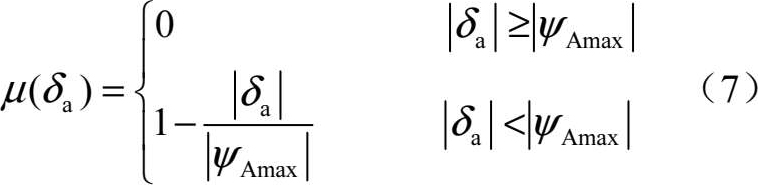
μ ( δ a )越大,UCAV相对目标RCS越小,对UCAV越有利。式中, δ a 为UCAV速度矢量与视线夹角,求解公式为
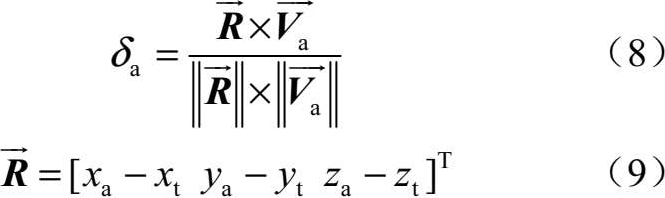
求解UCAV远距空战航迹规划就是在满足UCAV自身约束条件下,寻找使得给定的代价函数最小的控制量的过程 [10] 。考虑一般的连续性Bolza最优控制问题,最小代价函数为
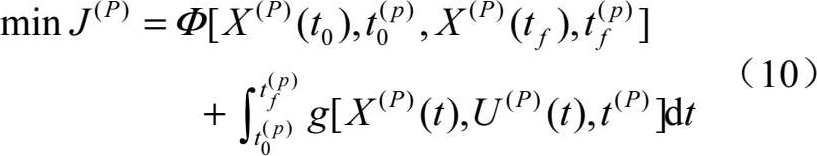
状态微分方程为
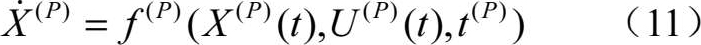
路径约束:
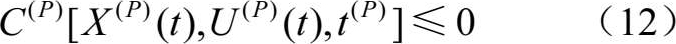
端点约束:
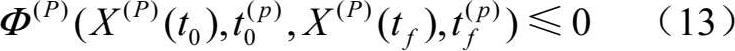
段间连接约束:
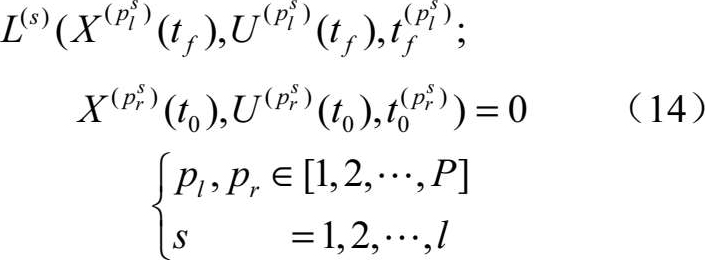
其中,控制变量 U ( t )= [ α ( t ) γ ( t ) δ ( t )] T ,状态变量 X ( t )=[ x a ( t ) y a ( t ) z a ( t ) V a ( t ) γ a ( t ) ψ a ( t )] T , p l 、 p r 表示分段处左右两端, s 表示第 s 个分段点。
1.3.1末端约束
根据UCAV分段航迹规划的目的不同,每段航迹的末端约束条件也存在差异,结合航迹规划的目的,分段航迹末端约束为:
(1)UCAV规避目标威胁段末端约束条件。
由于要求UCAV摆脱目标的探测与攻击威胁,末端点必须使UCAV位于目标威胁区之外。故UCAV对相对目标的方位角 θ r 约束为

(2)UCAV低可见接敌段末端约束条件。
UCAV低可见接敌的目的是达到对目标的攻击条件,首先要使目标进入UCAV的攻击包络内,即

1.3.2路径约束
根据UCAV远距占位航迹规划不同阶段的目的不同,其每一段的全局约束条件也不同。在规避目标威胁段航迹规划中,要求UCAV始终在目标的雷达最大探测距离之外,因此UCAV与目标相对距离限制为

式中,
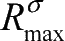 表示目标对UCAV的探测距离。同时,全局要满足UCAV自身飞行性能参数限制,即
表示目标对UCAV的探测距离。同时,全局要满足UCAV自身飞行性能参数限制,即
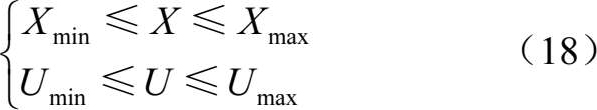
1.3.3分段连接约束
整个路径规划分为两段,因此只存在一个分段点,要求在分段点处,状态量与控制量左右连续,因此连接点约束为
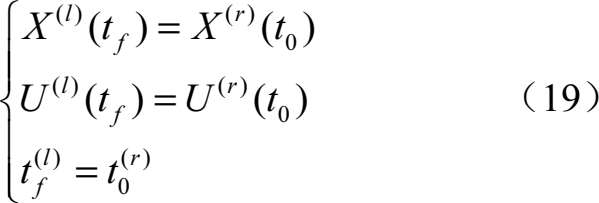
1.3.4最优化性能指标
(1)规划的第一段即规避目标威胁的任务需求来说,相对方位角调整得越快,目标对UCAV威胁性越小,即要求在尽可能短的时间达到满足UCAV规避约束条件的末端点,因此,将瞬时暴露威胁值,即使式(6)在整段规划时间域内进行积分,并取最小值,这就保证了UCAV可以最快地规避到目标的雷达最大探测角度之外。选取Lagrange型代价函数为
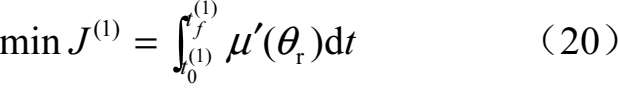
(2)对于低可见接敌来说,需要UCAV相对目标RCS值最小,根据RCS的特性分析,当UCAV机头指向目标时,RCS值最小,因此选取代价函数为
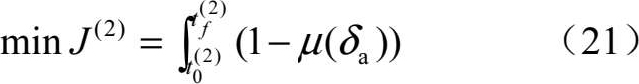
对式(21)进行寻优,既保证了UCAV速度指向目标,又满足了时间最短的约束条件。