





BP神经网络的全称为Back-Propagation Network,即反向传播网络。BP神经网络作为人工神经网络中应用最广的算法模型,具有完备的理论体系和学习机制。它模仿人脑神经元对外部激励信号的反应过程,建立多层感知器模型,利用信号正向传播和误差反向调节的学习机制,通过多次迭代学习,成功地搭建出处理非线性信息的智能化网络模型。
单层BP神经网络如图1-1所示。其中,x j (j=1,2,…,N)为神经元j的输入信号,w ij 为连接权重;u i 为输入信号线性组合后的输出,也是神经元i的净输入;θ i 为神经元的阈值;v i 为经阈值调整后的值;f(●)为神经元的激励函数。输入信号在单层感知器中传递的数学模型为:
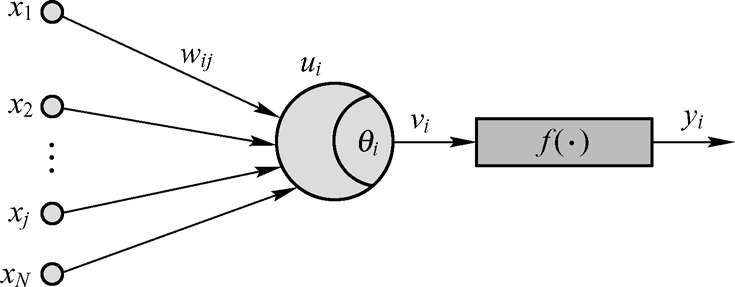
图1-1 单层BP神经网络示意图

f(●)为BP神经元的激励函数,比较常见的激励函数包括logsig函数、tansig函数等。以logsig函数为例,其表达式为:
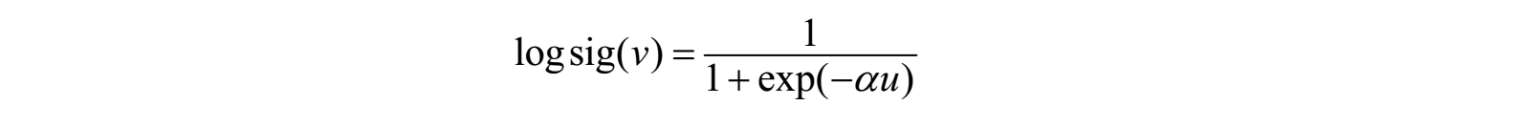
其中, α 为常数。
对于tansig函数,其表达式为:

其中, α 为常数
多层神经网络的结构如图1-2所示,原理与单层神经网络一样,本书将在后面的章节中进行详细介绍。

图1-2 多层BP神经网络结构示意图
MATLAB神经网络工具箱中包含了许多用于BP神经网络分析与设计的函数,其中BP神经网络常用的函数如表1-1所示。
表1-1 BP神经网络的常用函数表
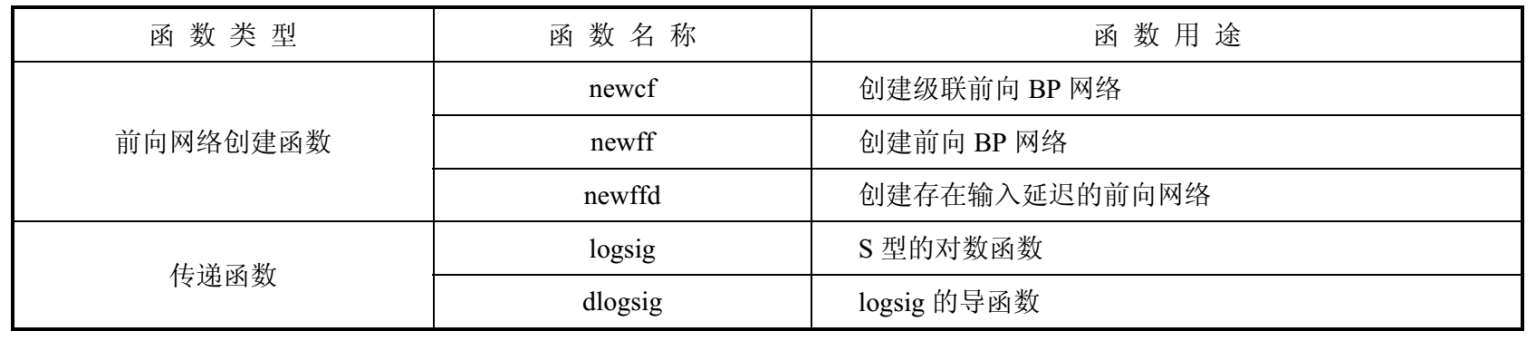
续表

本节将简要介绍其中比较常用的函数。
该函数用于创建级联前向BP神经网络,调用格式为:
① net=newcf
② net=newcf(PR,[S1,S2,…,S(N-1)],{TF1,TF2,…,TF(N-1)},BTF,BLF,PF)
③ net = newcf(P,T,[S1,S2,…,S(N-l)],{TF1,TF2,…,TFN}, BTF,BLF,PF,IPF,OPF,DDF)
其中,
net=newcf:用于在对话框中创建一个BP神经网络;
PR:每组输入(共有R组输入)元素的最大值和最小值组成的R×2维矩阵;
Si:第i层的长度,共计N-1层;
TFi:第i层的传递函数,默认为“tansig”;
BTF:BP网络的训练函数,默认为“trainlm”;
BLF:权值和阈值的BP学习算法,默认为“learngdm”;
PF:网络的性能函数,默认为“mse”;
值得注意的是,参数TFi可以采用任意的可微函数,如tansig、logsig和purelin等;训练函数可以是任意的BP训练函数,如trainlm、trainbfg、trainrp和traingd等。
实际测试表明,traingd比trainlm要慢得多,但由于它占用内存比较少,所以不存在死机的问题,对于配置比较低的计算机可以考虑用该训练函数。
该函数用于创建一个前向BP网络,调用格式为:
① net=newff
② net=newff(PR,[S1,S2,…,S(N-l)],{TF1,TF2,…,TFN}, BTF,BLF,PF,IPF,OPF,DDF)
③ net=newff(P,T,[S1,S2,…,S(N-l)],{TF1,TF2,…,TFN}, BTF,BLF,PF,IPF,OPF,DDF)
其中,
net=newff:用于在对话框中创建一个前向BP网络。
其他参数含义见newcf。
该函数用于创建一个存在输入延迟的前向网络。调用格式为:
① net=newfftd
② net=newfftd(PR,[S1,S2,…,S(N-l)],{TF1,TF2,…,TFN}, BTF,BLF,PF)
③ net=newfftd(P,T,ID,[S1,S2,…,S(N-l)],{TF1,TF2,…,TFNl},BTF,BLF,PF,IPF,OPF,DDF)
其中,
net=newfftd:用于在对话框中创建一个BP网络;
ID:输入延迟向量;
其他参数参见newcf。
该函数为梯度下降权值/阈值学习函数,它通过神经元的输入和误差,以及权值和阈值的学习速率来计算权值/阈值的变化率。调用格式为:
① [dW,ls]=learngd(W,P,X,N,A,T,E,gW,gA,D,LP,LS)
② [db,ls]=learngd(b,ones(1,Q),Z,N,A,T,E,gW,gA,D,LP,LS)
③ info=learngd(code)
其中,
W:S×R维的权值矩阵;
b:S维的阈值向量;
P:Q组R维的输入向量;
ones(1,Q):产生一个Q维的输入向量;
Z:Q组S维的加权输入向量;
N:Q组S维的输入向量;
A:Q组S维的输出向量;
T:Q组S维的层目标向量;
E:Q组S维的层误差向量;
gW:与性能相关的S×R维梯度;
gA:与性能相关的S×R维输出梯度;
D:S×S维的神经元距离矩阵;
LP:学习参数,可通过该参数设置学习速率,设置格式如LP.lr=0.01;
LS:学习状态,初始状态下为空;
dW:S×R维的权值或阈值变化率矩阵;
db:S维的阈值变化率向量;
ls:新的学习状态;
learngd(code):根据不同的code值返回有关函数的不同信息,包括以下内容。
pnames—返回设置的学习参数;
pdefaults—返回默认的学习参数;
needg—如果函数使用了gW或gA,则返回1。
该函数为梯度下降动量学习函数,它利用神经元的输入和误差、权值/阈值的学习速率和动量常数来计算权值/阈值的变化率。调用格式为:
① [dW,LS]=learngdm(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)
② [db,LS]=learngdm(b,ones(1,Q),Z,N,A,T,E,gW,gA,D,LP,LS)
③ info=learngdm(code)
各参数的含义请参见learngd。
该函数用于对神经网络进行训练。调用格式为:
① [net,tr,Y,E,Pf,Af]=train(NET,P,T,Pi,Ai)
② [net,tr,Y,E,Pf,Af]=train(NET,P,T,Pi,Ai,VV,TV)
其中,
NET:待训练的神经网络;
P:网络的输入信号;
T:网络的目标,默认为0;
Pi:初始的输入延迟,默认为0;
Ai:初始的层次延迟,默认为0;
VV:网络结构确认向量,默认为空;
net:函数返回值,训练后的神经网络;
tr:函数返回值,训练记录(包括步数和性能);
Y:函数返回值,神经网络输出信号;
E:函数返回值,神经网络误差;
Pf:函数返回值,最终输入延迟;
Af:函数返回值,最终层延迟。
NET=init(net)
其中,
NET:返回参数,表示已经初始化后的神经网络;
net:待初始化的神经网络。
NET为net经过一定的初始化修正而成。修正后,前者的权值和阈值都发生了改变。
传递函数的作用是将神经网络的输入转换为输出。
① a = purelin(n);
② a = tansig(n);
③ a = logsig(n);
④ a = hardlim(n);
各类传递函数的变化情况如图1-3所示。
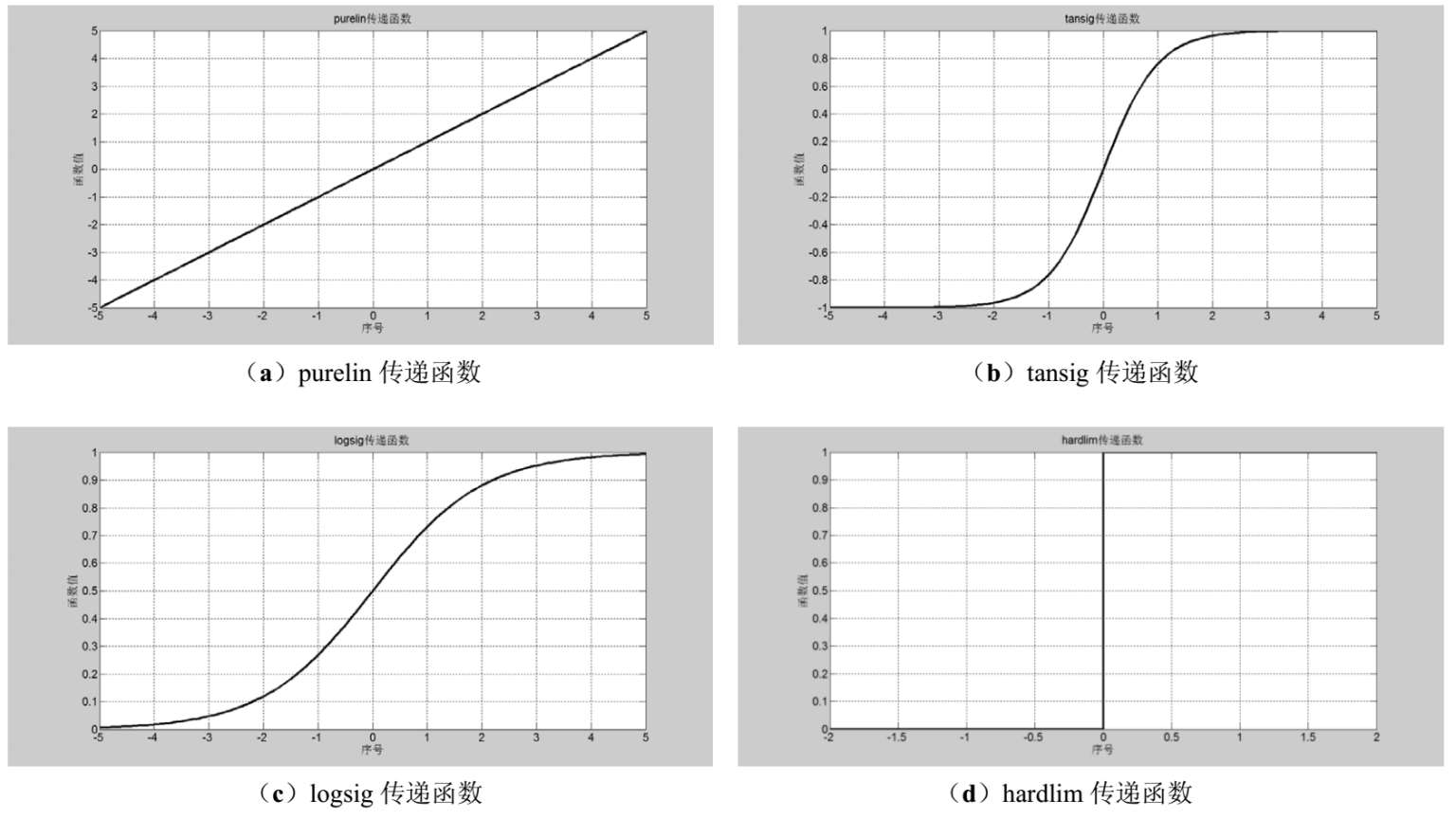
图1-3 神经网络传递函数的变化情况
值得注意的是,对logsig函数求导,有:
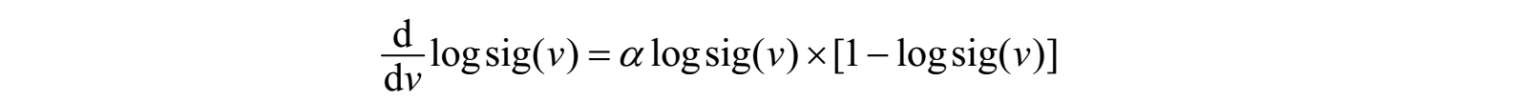
对于tansig函数,其导数为:
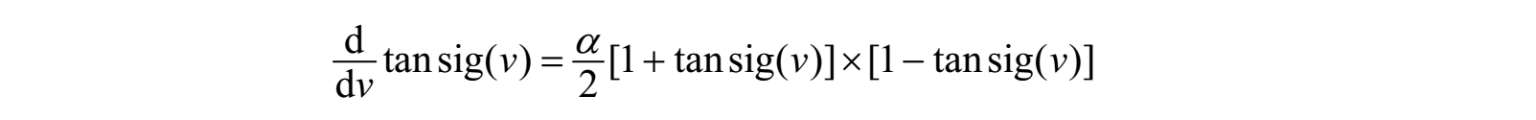
其中, α 为常数。
logsig函数和tansig函数的这些性质十分重要,因为BP神经网络的学习采用的是基于最小二乘的误差反向传递算法,学习时采用的步长与误差的梯度成正比,而误差的梯度通常是大量传递函数导数的线性叠加。因此,将导数运算转换为乘法运算可以节省大量的计算时间,同时也提高了运算的精度,这对于编程设计与使用神经网络是有极大好处的。