




在第 1 章中,针对太阳系的实际背景,曾提到限制性(n+k)体问题 [7,8] 。例如,主带小行星群中两颗小行星之间的距离可以很近,如果考虑它们之间的引力作用,那么太阳、木星和这两颗小行星就构成一个限制性(2+2)体问题;在地球赤道上空一个定点处发射两颗以上几吨重的地球“静止”卫星,相互之间的距离若为百米量级,在精度要求较高的问题中就需要考虑它们之间的相互引力作用,在此情况下,作为椭球体的地球(相当于一个质量密度均匀的球体和椭球体赤道的“多余”部分,视为两个大天体)和两个卫星同样构成一个限制性(2+2)体问题 [8] 。在深空探测中也有可能出现这样的状态,如在某个特殊位置附近定点多个探测器,相互之间的引力作用又不可忽视,在此情况下与两个相应的大天体就构成上述限制性(2+k)体问题。
以圆型限制性(2+2)体问题为例,对于每一个小天体的运动,实际上即对应一种特殊的受摄圆型限制性三体问题,就两个小天体中的一个而言,与其靠近的另一小天体的引力就是一个摄动源。在这样的力学模型中,小天体的运动状态是否与单一的圆型限制性三体问题相近,应予考查,正是由于这一原因,故将这类限制性问题也列入本章与限制性(2+1)体问题作对比性的论述。
为了与圆型限制性三体问题的讨论相对应,不妨将原会合坐标系中的基本方程式(3.20)改为下列形式 [6] ,即
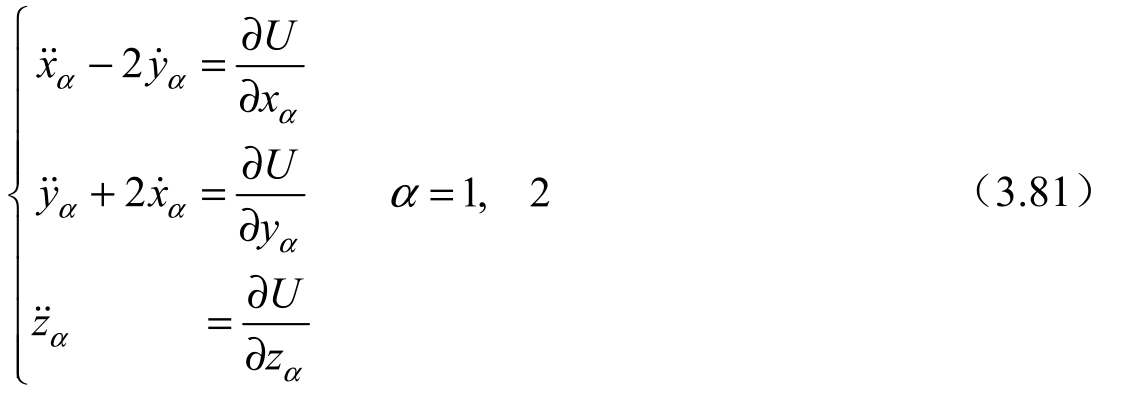
该式中的U是系统的“引力位”,即
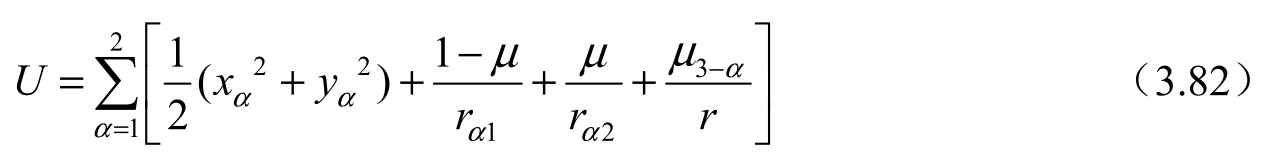
其中
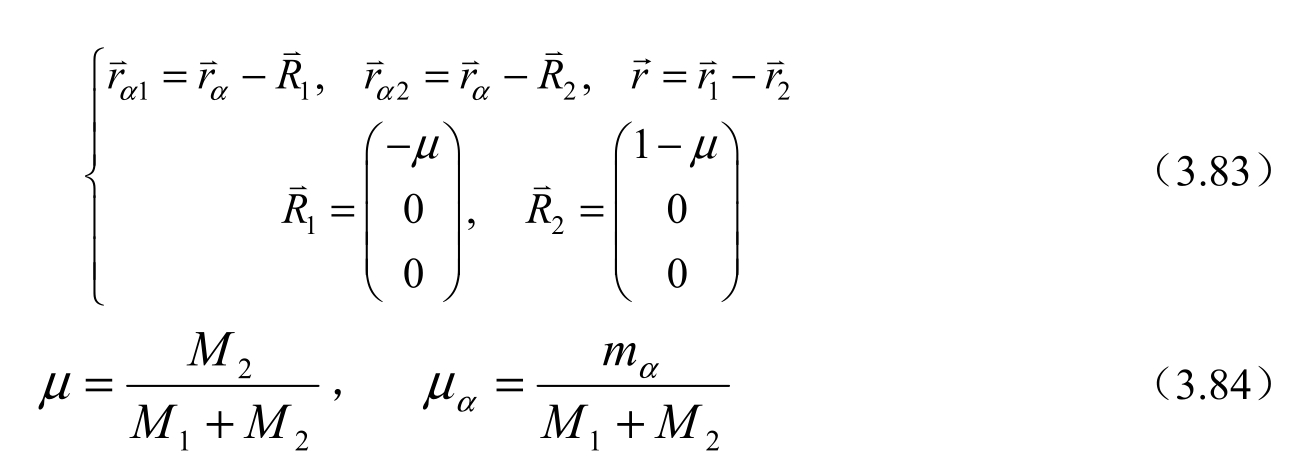
显然,对于每一个小天体的运动,无积分存在,但对整个系统而言,却有一个广义Jacobi积分存在,即

与圆型限制性三体问题类似,仅找到这一积分,进一步的研究内容请见下一章的第4.5节。