




随着航天技术的发展和太阳系探测的需求,从20世纪50年代人造地球卫星上天后,各类航天器相继升空,要保证航天器进入目标轨道后顺利地完成预定任务,就必须提供达到一定精度的运行轨道,因此,相应的轨道确定工作就成为航天领域的一项最基本的也是最重要的工作之一。
考虑到具体需求和阐述的方便,本书以人造地球卫星的轨道确定为主线展开论述,但其涉及的基本原理、数学模型的建立及具体处理方法等内容,同样适用于其他各类航天器,只是具体细节有所差异而已。
表达各类航天器轨道运动的基本状态量是:在所采用的空间坐标系中,相对中心天体的位置矢量
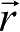 和速度矢量
和速度矢量
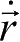 ;若是环绕型探测器(即中心天体的卫星,如地球卫星),还可采用椭圆轨道根数(或称 Kepler 根数),常用符号a,e,i,Ω,ω,M 来表示,其中a和e是轨道半长径和偏心率,表示椭圆的大小和形状,i是轨道倾角,即轨道平面与坐标系基本平面(xy坐标面,对地球卫星来说是赤道面)的夹角,Ω是升交点经度(或升交点赤经),它是从xy坐标面上x轴方向(如春分点方向)沿坐标面向东计量到轨道升交点(即卫星从南到北与坐标面的交点)的一段弧,ω是轨道上近星点的幅角,它是从升交点沿轨道(卫星运动方向)计量到近星点的一段弧,M称为平近点角,是按卫星平运动n计算从近星点起量的一种近点角,即
;若是环绕型探测器(即中心天体的卫星,如地球卫星),还可采用椭圆轨道根数(或称 Kepler 根数),常用符号a,e,i,Ω,ω,M 来表示,其中a和e是轨道半长径和偏心率,表示椭圆的大小和形状,i是轨道倾角,即轨道平面与坐标系基本平面(xy坐标面,对地球卫星来说是赤道面)的夹角,Ω是升交点经度(或升交点赤经),它是从xy坐标面上x轴方向(如春分点方向)沿坐标面向东计量到轨道升交点(即卫星从南到北与坐标面的交点)的一段弧,ω是轨道上近星点的幅角,它是从升交点沿轨道(卫星运动方向)计量到近星点的一段弧,M称为平近点角,是按卫星平运动n计算从近星点起量的一种近点角,即
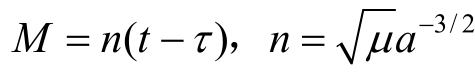
其中,μ是中心天体的引力常数,τ是卫星过近星点的时刻。
关于基本状态量的选择,这里有一点要说明:如果需要定轨软件适用于各类航天器,包括环绕型的卫星轨道和“非环绕型”的转移轨道(可以是椭圆轨道,亦可以是双曲线轨道),那么航天器的位置矢量和速度矢量
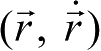 显然是基本状态量的唯一选择对象,如有需要,可以将定轨结果转换成相应的轨道根数。
显然是基本状态量的唯一选择对象,如有需要,可以将定轨结果转换成相应的轨道根数。
如果定轨对象是环绕型探测器,可以采用椭圆轨道根数作为基本状态量,但由于对目标天体探测的需要,中低轨卫星的轨道偏心率e通常较小,相应的ω和M两根数难以确定,为了使相应的方法和计算公式能适用于各种偏心率(0≤e<1),通常采用另一类根数,即消除小偏心率困难(适用于0≤e<1)的无奇点根数,即
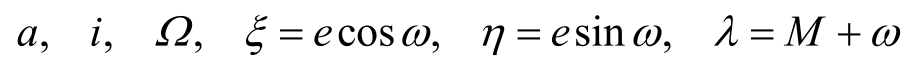
对于高轨卫星(如地球同步卫星),还会遇到偏心率e和轨道倾角i都很小的情况,此时除ω和M外,Ω亦难以确定,这将采用另一类同时消除小偏心率和小倾角困难(即适用于0≤e<1和0≤i<180°)的无奇点根数,即
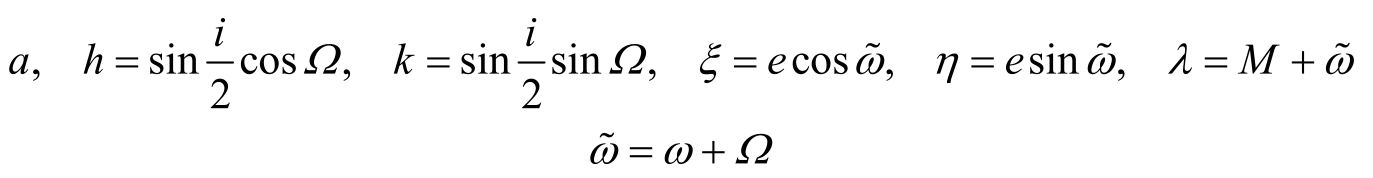
通常称上面两式定义的根数分别为第一类和第二类无奇点根数。
关于常数系统,除一套天文常数外,主要涉及各力学因素对应的物理参数,如地球引力场参数,它与测站坐标系统有关,相应的选择应该是一个自洽系统。