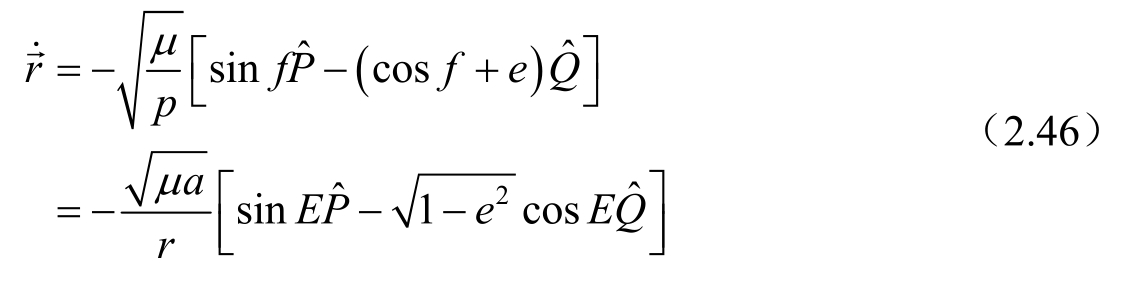卫星(环绕型航天器)运动对应一个受摄力学系统,最常用的数学模型即受摄二体问题,二体问题是其基本参考模型,该模型的解就作为解决相应问题的基础。尽管在近代几本有关天体力学方法的基础著作和教材中 [3~6] ,对二体问题已有不同的介绍,但作为定轨的需求,对此基础问题仍需作些必要的阐述,并针对解决实际问题的具体情况,着重针对椭圆运动,给出常用关系式。
对于二体问题,两个天体P 0 和p均作为质点对待,分别将该两天体的质量记为M和m (对于卫星,可取m=0),讨论天体p相对天体P 0 的运动。此时可将运动方程,即式(2.1)改写为下列形式,即

其中,
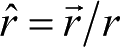 是中心天体P
0
到运动天体p方向的单位矢量。相应的运动坐标系O-XYZ (见图 2.1)的原点O在天体P
0
上(注意:此时P
0
是质点),但基本平面(XY坐标面)可有多种选择。根据轨道力学问题的具体特点,对于人造地球卫星的运动问题,XY平面与地球赤道面一致,而处理太阳系中大行星和小行星的运动问题,往往取日心黄道面作为XY平面,但在讨论自然卫星运动时(特别是离相应大行星较近的自然卫星),则与讨论人造地球卫星的运动有些相似,取各大行星的赤道面作为XY平面。至于X 轴方向的确定,对于太阳系,无论是讨论行星运动,还是人造地球卫星的运动,几乎都是取春分点方向作为X 轴方向,这在前面第 1章中已有相应的阐述。
是中心天体P
0
到运动天体p方向的单位矢量。相应的运动坐标系O-XYZ (见图 2.1)的原点O在天体P
0
上(注意:此时P
0
是质点),但基本平面(XY坐标面)可有多种选择。根据轨道力学问题的具体特点,对于人造地球卫星的运动问题,XY平面与地球赤道面一致,而处理太阳系中大行星和小行星的运动问题,往往取日心黄道面作为XY平面,但在讨论自然卫星运动时(特别是离相应大行星较近的自然卫星),则与讨论人造地球卫星的运动有些相似,取各大行星的赤道面作为XY平面。至于X 轴方向的确定,对于太阳系,无论是讨论行星运动,还是人造地球卫星的运动,几乎都是取春分点方向作为X 轴方向,这在前面第 1章中已有相应的阐述。
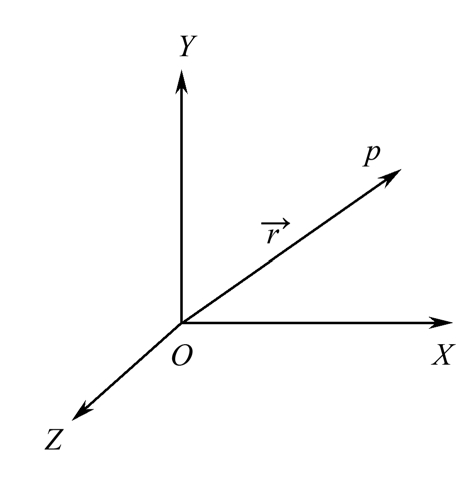
图2.1 运动坐标系O-XYZ
为了简便,常记

方程(2.5)对应的是有心力问题,不仅是可积的(这里的可积是指上述微分方程的解可以写成求积形式),而且可以具体给出六个积分的完整表达式,并在给出六个积分的同时,指出相应常微分方程的特征,从而可以使读者重温常微分方程求解的基本方法。下面将作具体介绍。
根据有心力的性质,可直接写出方程(2.5)的动量矩积分,由该方程亦容易推出该积分。若记
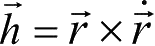 为面积速度矢量,则由方程(2.5)可得
为面积速度矢量,则由方程(2.5)可得
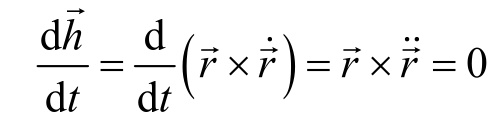
这表明
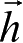 为一常矢量,天体p相对P
0
的运动为一平面动。相应的动量矩积分可写成
为一常矢量,天体p相对P
0
的运动为一平面动。相应的动量矩积分可写成

其中,
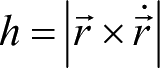 为面积速度常数,单位矢量ˆR表示面积速度方向,它是天体运动平面的法向单位矢量。
为面积速度常数,单位矢量ˆR表示面积速度方向,它是天体运动平面的法向单位矢量。
如果用天体运动轨道来描述动量矩积分的几何意义,则可引用辅助天球(见图2.2),图中大圆AA′和BB′分别表示基本平面(XY坐标面)和运动天体轨道在辅助天球上的投影,
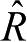 方向为轨道面法向,i是卫星轨道面与基本平面的夹角,Ω为轨道升交点方向N (或称节点)的经度(或称赤经),从X 方向起量。利用球面三角形的余弦公式(或用坐标旋转的方法),不难导出法向单位矢量
方向为轨道面法向,i是卫星轨道面与基本平面的夹角,Ω为轨道升交点方向N (或称节点)的经度(或称赤经),从X 方向起量。利用球面三角形的余弦公式(或用坐标旋转的方法),不难导出法向单位矢量
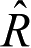 在坐标系O-XYZ中的表达式为
在坐标系O-XYZ中的表达式为
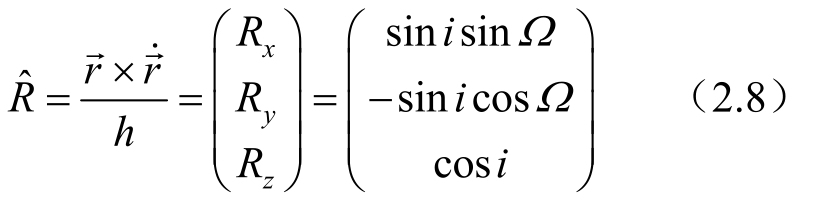
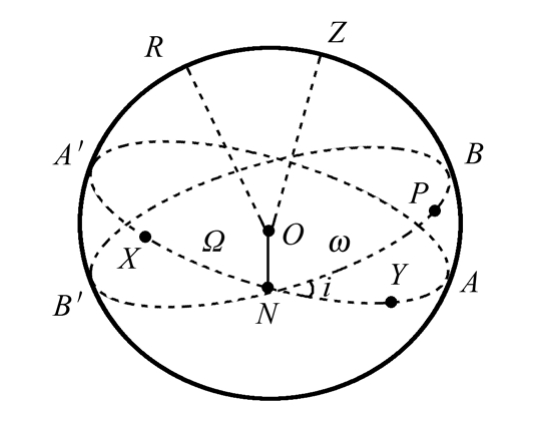
图2.2 辅助天球
动量矩积分公式(2.7)包含了h,i,Ω三个积分常数,h是面积速度的两倍,i,Ω则确定了轨道平面的空间方向。
从公式(2.7)的推导过程不难看出,只要是有心力,即

必存在公式(2.7),并不要求如同方程(2.9)右端的
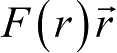 那种简单形式,λ,φ是常用的球坐标的另两个分量,即经、纬度。
那种简单形式,λ,φ是常用的球坐标的另两个分量,即经、纬度。
既然是平面运动,而相应的平面已由(i,Ω)确定,那么,接着就可在这一确定的平面内讨论降阶后的方程。引入平面极坐标(r,θ),运动方程(2.5)的径向分量为

而横向分量为
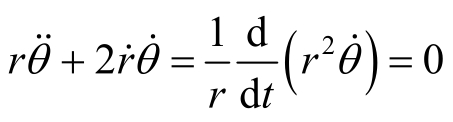
此方程给出一个积分

由空间极坐标(三个轴方向的单位矢量分别记作
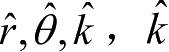 为前面的
为前面的
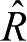 )中
)中
 的表达式为
的表达式为

可得

这表明公式(2.11)就是动量矩积分公式(2.7)的标量形式,或称面积积分。方程(2.10)和方程(2.11)构成了平面运动系统对应的三阶常微分方程,需要再寻找三个独立积分。
上述方程组的特点是不显含自变量 t,由常微分方程的基本知识可知,对于这类方程,通过分离自变量t的方法可使它降一阶,即能够首先讨论r对θ的变化规律。为此,记
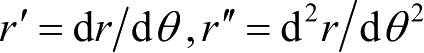 ,由方程(2.7)得
,由方程(2.7)得
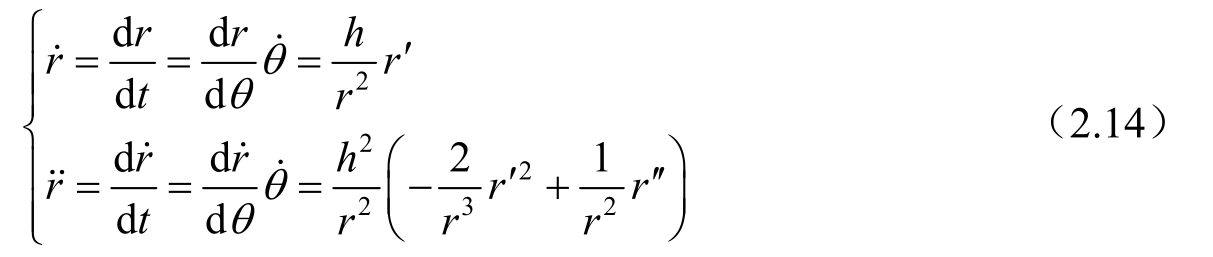
将这一关系代入方程(2.10),即可给出r对θ的二阶方程。但相应的方程仍不便于求解,如果在降阶的同时,再作变量变换,即

有
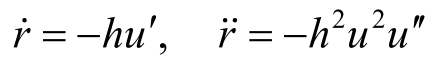
利用这一关系即可得到u对θ的一个二阶常系数线性方程为

这显然是可积的。容易给出一轨道积分为

e和ω为两个新积分常数。这是一圆锥曲线,在一定条件下它表示椭圆,中心天体(即O点)在其一个焦点上,考虑到本书的内容,主要讨论椭圆运动,至于抛物线和双曲线轨道,实为非环绕型轨道,这里不再介绍,如有需要,读者可见参考文献[8]所提及的《航天器轨道理论》一书的第2章。对于椭圆,可令

那么公式(2.11)和方程(2.17)又可写成
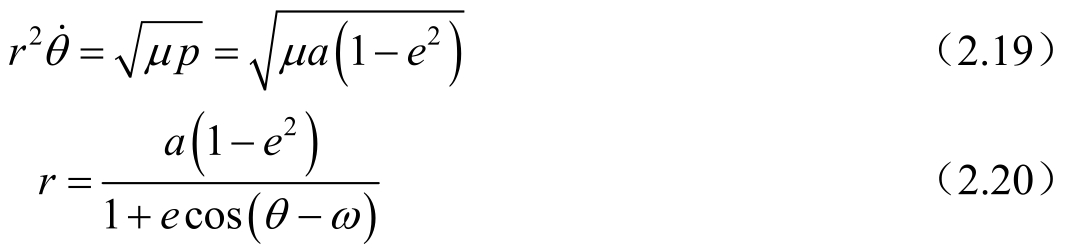
积分常数h由a代替,这里p是椭圆的半通径,a是半长径,e是偏心率,ω则称为运动天体过近星点P的幅角,因在P点方向θ=ω时,r达到最小值,故称P点方向为近星点方向。注意,近星点幅角ω和极坐标变量θ都是从节点N方向起量的,这在二体问题中无区别,当有摄动时,椭圆随时间变化,升交点方向也在变化,ω应从这变化的升交点方向起量,而极坐标变量θ却仍应从一个定义的不变方向起量,两者是有区别的。
将r=r(θ)的关系代入方程(2.19),原则上可以给出最后一个与时间t有关的积分。这里暂时放一下,先导出椭圆运动的几个常用关系。由公式(2.19)和式(2.20),经简单的运算可得

此为活力公式。另外,既然是椭圆运动,那么运动天体的向径在一个周期T内扫过的面积就是椭圆的面积:
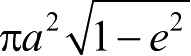 ,由此可知两倍的面积速度h为
,由此可知两倍的面积速度h为
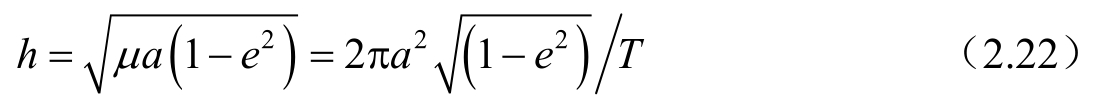
整理后可得

若引进平运动角速度
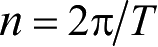 ,则式(2.23)又可写成
,则式(2.23)又可写成

这两个表达式就是万有引力定律导出的开普勒(Kepler)第三定律。
这里要说明一点:关于活力公式(2.21),与动量矩积分公式(2.7)的推导类似,也可直接由运动方程(2.5)两端点乘
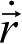 获得,即
获得,即
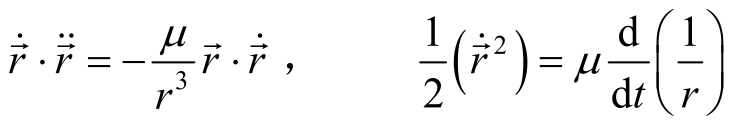
由此立即可得出一积分公式,即
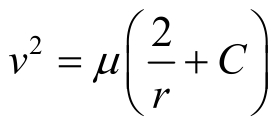
此即活力积分,实际上就是一般N (N≥2)体问题10个经典积分中的能量积分在上述二体相对运动中的转型。但从二体问题求解的角度寻找六个独立积分的过程来看,上述处理直至轨道积分公式(2.17),共给出五个独立积分,是为了进一步寻找10个经典积分以外的另两个独立积分,其中之一为轨道积分,尽管它对应二阶方程,与活力积分一共只有两个是独立的,故称式(2.21)为活力公式为宜。剩下一个独立积分必与自变量t(轨道运动的反映)有关。
为了运算方便,在寻找第六个积分时,不直接对方程(2.19)按dθdt求解,而是利用式(2.21)按
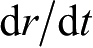 积分,有
积分,有
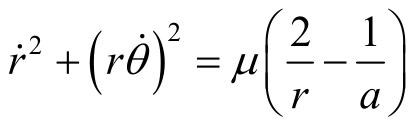
即
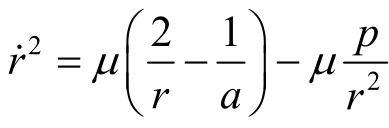
通过式(2.24)消去μ,整理后得

对于椭圆轨道,r的极大和极小值分别为
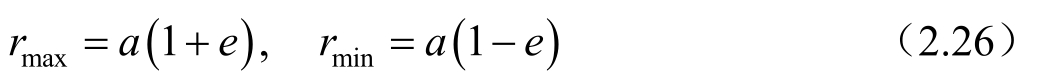
因此有
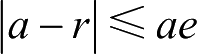 ,故可按下式引入辅助量E,即
,故可按下式引入辅助量E,即
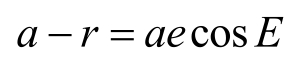
或写成

代入式(2.25)可得
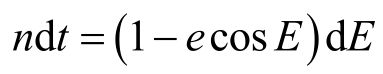
由此便可得出第六个积分,即

这又称为开普勒方程,τ是积分常数。当t=τ时,E=0,相应的r=a (1-e)=r min ,故τ就是运动天体过近星点的时刻。
最后引进两个角度 f 和M,定义为

f,M和E是三个角度量,分别称为真近点角、平近点角和偏近点角,都是从近星点开始计量,E的几何意义见图2.3。
图2.3中O是椭圆焦点(也是坐标系原点),O′是辅助圆的圆心。显然,在二体问题中,公式(2.7)可简化为下列形式,即

上述六个独立积分常数实为描述天体运动轨道的一组独立参数,通常称为轨道根数,只要初始条件给定,它们就完全被确定。根数a,e是确定轨道大小和形状的参数;i,Ω和ω是轨道平面和拱线(长半轴)的空间定向参数;而第六个根数τ通常是被三种近点角所代替,特别是平近点角M常被引用,三种近点角本身同时包含时间t,而不是常数,随t而变化,故也被称为时间根数。特别要强调一点:上述六个轨道根数a,e,i,Ω,ω,M(f,E),也常被称为开普勒根数,这一称谓与天体力学发展的历史相关。
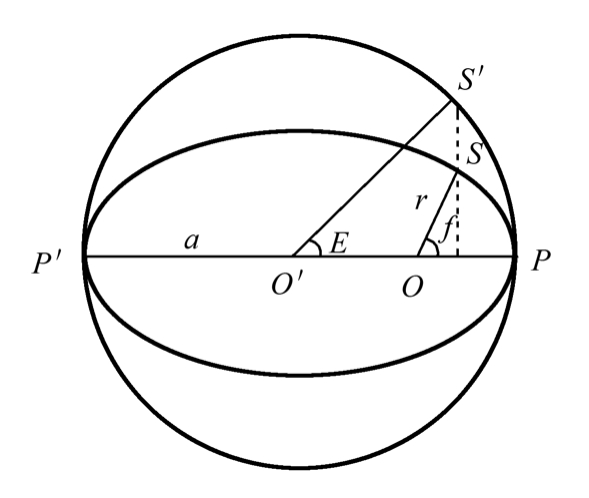
图2.3 椭圆轨道和辅助圆
上述六个积分已完全确定了二体问题意义下卫星的运动,但这六个积分的表达形式在某些实际问题的使用上多有不便,有必要在其基础上导出一些常用的关系式。下面将根据定轨工作的需要整理,所涉及的量不外乎六个轨道根数、时间 t、各种近点角、向径和速度等。
首先从图2.3和开普勒方程(2.28)不难看出,三种近点角的象限关系很清楚,它们同时处在[0,π]或[π,2π]区间上,这是一个很重要的关系,它们之间的联系为
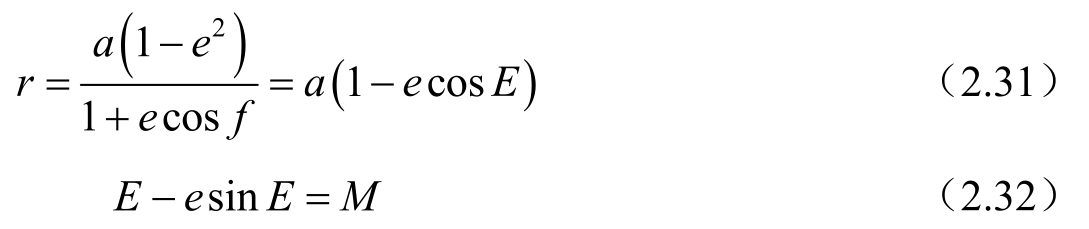
另外,根据椭圆的性质可知,图2.3中的
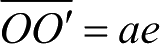 ,于是有
,于是有

由此可导出
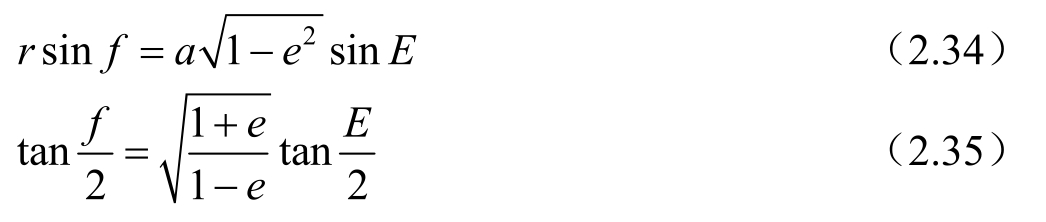
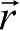 和速度矢量
和速度矢量
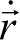 的表达式
的表达式
作为二阶方程(2.5)的完整解,应该有

既然六个积分已得到,那么可以写出式(2.36)的具体形式。这里的积分常数C 1 ,…,C 6 是前面的六个轨道根数,其中C 6 是τ,如果改用平近点角M,式(2.36)中的t将包含在M中。
显然有
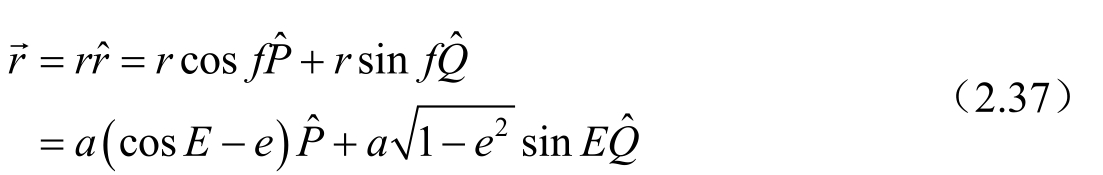
其中,
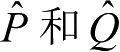 分别表示近星点和半通径方向的单位矢量。通过坐标旋转,很容易给出它们在直角坐标系O-XYZ中的表达式。若在以轨道面作为xy平面的直角坐标系中,x轴指向近星点方向,则相应的单位矢量
分别表示近星点和半通径方向的单位矢量。通过坐标旋转,很容易给出它们在直角坐标系O-XYZ中的表达式。若在以轨道面作为xy平面的直角坐标系中,x轴指向近星点方向,则相应的单位矢量
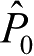 有下列形式,即
有下列形式,即

于是O-XYZ坐标系中
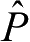 的表达式将由下列矩阵旋转得到
的表达式将由下列矩阵旋转得到
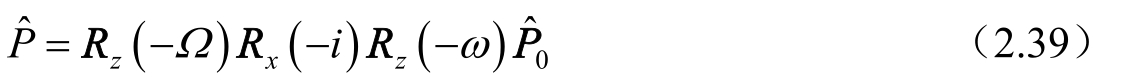
其中三个旋转矩阵的形式为
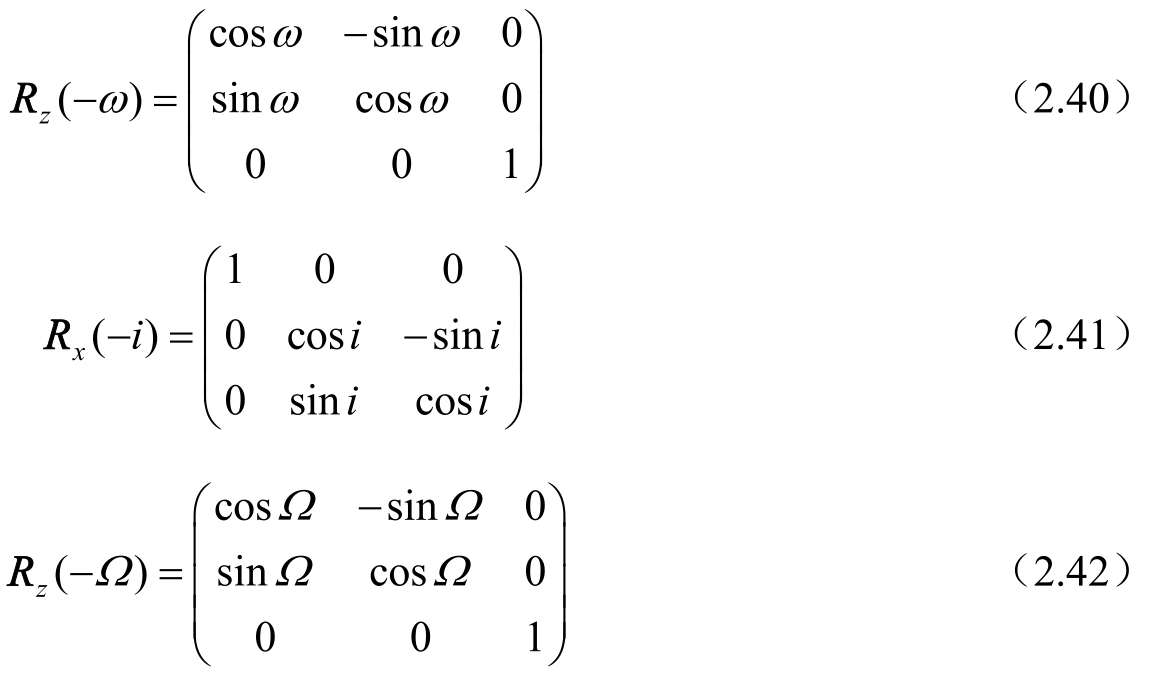
至于
 的表达式,只要将
R
z
(-ω)改为
R
z
(α),α=-(ω+90)°即得。
的表达式,只要将
R
z
(-ω)改为
R
z
(α),α=-(ω+90)°即得。
为了某些应用的需要,下面将
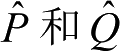 的具体表达式写出,即
的具体表达式写出,即

关于
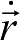 ,根据二体问题的性质,由
,根据二体问题的性质,由
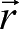 的表达式(2.37)可得
的表达式(2.37)可得

由公式(2.30)给出的
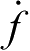 或由方程(2.32)给出的E,可具体写出
或由方程(2.32)给出的E,可具体写出
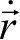 的表达式为
的表达式为