




第1章已针对太阳系探测中航天器的运动引进了相应的时空参考系,接着就需要了解各类航天器在运行过程中的受力状况,从而建立相应的数学模型。关于数学模型的建立,既要尽量符合真实的物理背景,又要有利于问题的解决,真正达到实际应用的目的。
既然是太阳系探测,那么首先就要了解各类航天器在太阳系中运行的力学环境。太阳系是一个十分复杂的力学系统,除了作为这一力学系统主天体存在的太阳外,还有8个大行星和数量众多的小行星及自然卫星、彗星和空间尘埃等。就目前来看,任何一个航天器的出现,除非碰撞发生,都不会改变太阳系中其他天体的运动状态。
如果将航天器和所有影响它的n个引力源(包括非引力源,如太阳辐射等)都处理成“质点”(暂且不考虑非质点引力或非引力的一些具体细节,因为这不会影响对问题的阐述),则形成一个(n+1)体系统,数学上就构成一个(n+1)体问题。本书所要论述的问题是:一个质量可忽略的航天器在另外n个运动状态完全确定的“天体引力”(确切地说为相应的外力源)作用下的运动,这一动力学问题就称为限制性(n+1)体问题,它与一般(n+1)体问题的提法和研究内容有重大区别。当n+1=3时,就是天体力学(或轨道力学)中最著名的“限制性三体问题”。限制性问题与非限制性问题不是简单的名称差别,由于待研究的运动小天体的质量小到可以忽略,这将导致在数学处理方法上的重大差别。例如一般三体问题,除存在10 个经典积分外,无其他动力学信息,而限制性三体问题则不然,除该系统中两个大天体的运动状态能完全确定外,又可给出另一个小天体特有的运动特征,这对研究自然小天体(如小行星),或各类航天器的运动,都是极其重要的。
根据太阳系演化至今的现状,大天体、小天体和航天器运动中的主要外力源至多有两个,即使探测质量较小的小行星也不例外,包括探测器从地球附近飞往目标小行星的全过程中(无论采用何种方式)。对于各大行星的运动,主要外力源只有一个,就是太阳,其他外力源都是摄动源(即小扰动)。小行星运动主要的外力源是太阳或一个大行星;自然卫星的运动,主要外力源是相应的大行星;人造地球卫星的运动,主要外力源是地球;远地卫星的运动(如月球探测器在转移轨道段的运动),主要外力源是地球和月球;深空探测器(探测大行星或自然卫星)的运动,主要外力源是太阳,或大行星,或目标行星及其自然卫星。除两个主要外力源外,其他力源(包括上述非质点引力和非引力等)均可处理成摄动源。因此,在现实的太阳系中,研究各类航天器的运动,就轨道力学而言,合理的数学模型只有两类:一类是环绕型航天器(即人造卫星)的轨道问题,主要外力源只有一个,即其环绕的中心天体,对应的是一个受摄二体问题;而另一类是非环绕型航天器(包括各种空间探测器)的轨道问题,主要外力源有一个或两个,对应的是一个受摄限制性三体问题。
事实上,在太阳系动力学的研究过程中,受摄二体问题和受摄限制性三体问题就是两个有效的数学模型,而若形式上采用限制性四体或五体问题模型,相应的三个或四个大天体的运动问题本身就未解决,这类看似更精确或吸引人的模型,却无助于问题的解决。因此,在现实的太阳系中,处理大小天体和各类航天器的轨道运动问题时,除上述受摄二体问题模型外,就是受摄限制性三体问题模型,更确切地说,应该是受摄圆形限制性三体问题模型。
该模型对应的(n+1)体问题中,主要外力源作为中心天体,相应的质量记为M,坐标系原点取在其质心上,对于这样一个受摄二体模型,可归结为下列运动微分方程——常微初值问题,即
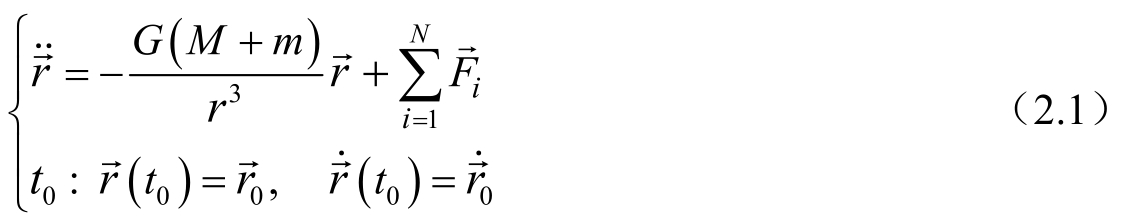
其中,G 是万有引力常数,m(m=0)是运动天体的质量,
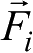 是应考虑的另外N=(n-1)摄动源对应的摄动加速度,这里的
是应考虑的另外N=(n-1)摄动源对应的摄动加速度,这里的
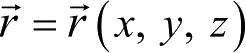 是运动天体在该坐标系中的位置矢量。
是运动天体在该坐标系中的位置矢量。
通常引用符号μ为

对于小天体(包括各种环绕型探测器),相应的质量可取m=0,那么表达小天体运动问题的式(2.1)即变为
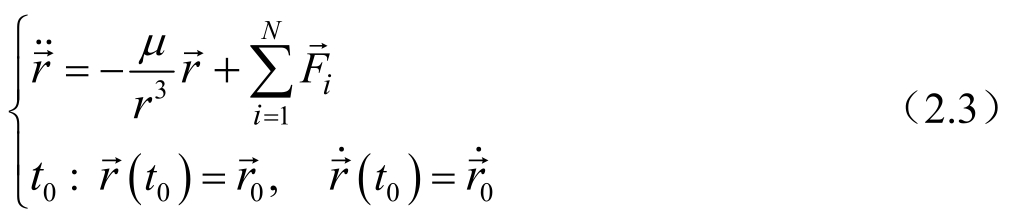
其中,μ(μ=GM)是中心天体的引力常数。例如研究人造地球卫星的运动,中心天体是地球,常用的符号μ(μ=GE)就是地心引力常数,其值为3.98603×10
14
(m
3
/s
2
)。对于一个地球低轨卫星,如果在300km高的近圆轨道上运行,地球中心引力加速度(μ/r
2
)约为9m/s
2
,而自然存在的各种摄动加速度
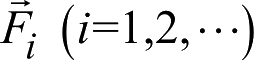 中最大的地球动力学扁率项的相对大小为10
-3
,运动方程(2.4)对应的就是一个典型的受摄二体问题,相应的运动轨道是一个缓慢变化的椭圆。如果该卫星有1T重,并同时存在持续的100N大小的机动力(这一卫星相当于一个机动平台),相应的机动加速度为0.1m/s
2
,这仍可看作一种摄动力,其相对大小也仅达到10
-2
,比月球环绕地球运动受到太阳的引力摄动(2×10
-2
)还小一些。对于这样一个空间机动平台的运动,采用受摄二体问题模型来研究它的运动规律仍然有效。
中最大的地球动力学扁率项的相对大小为10
-3
,运动方程(2.4)对应的就是一个典型的受摄二体问题,相应的运动轨道是一个缓慢变化的椭圆。如果该卫星有1T重,并同时存在持续的100N大小的机动力(这一卫星相当于一个机动平台),相应的机动加速度为0.1m/s
2
,这仍可看作一种摄动力,其相对大小也仅达到10
-2
,比月球环绕地球运动受到太阳的引力摄动(2×10
-2
)还小一些。对于这样一个空间机动平台的运动,采用受摄二体问题模型来研究它的运动规律仍然有效。
对应(n+1)=(1+1)的二体问题,就不再区分一般二体问题与限制性二体问题,因为方程中的μ=G (M+m)或μ=GM 均为常数,方程(2.1)或方程(2.3)的求解及其解的动力性特征没有任何差别。因此,就简单地称为二体问题。
受摄二体问题可提供满足一定精度的分析解 [1] ,因此,对于环绕型航天器的定轨问题,既可以采用数值法,亦可采用分析法。数值法是由运动微分方程(2.3)的数值解提供状态转移方程,而分析法则可直接引用方程(2.3)中第 2 个式子的分析解提供的状态转移方程,即1.5节定轨问题提法中的式(1.117)为

关于限制性三体问题,在本系列专著“航天器轨道力学理论与工程应用”第三本——《深空探测轨道理论与应用》(刘林,侯锡云著)中有详细阐述 [2] 。尽管其参考模型(圆形限制性三体问题)可以提供重要的动力学信息,在深空探测的轨道选择、目标轨道设计等方面起着重要作用,但直到目前为止还无法提供相应的分析解,因此,非环绕型的深空探测器的定轨问题,只能采用数值法解决,即直接由运动微分方程(2.3)的数值解提供状态转移方程及其相应的状态转移矩阵,详见第5章的相关内容。
从定轨角度来看,环绕型航天器与非环绕型航天器的定轨原理与方法并无原则差别,相应的动力学方程都是方程(2.3),其唯一的差别就是该方程的右函数中,除中心引力项
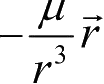 外,其他外力源的作用加速度项
外,其他外力源的作用加速度项
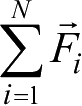 有所不同,对于环绕型航天器,该项相对中心引力项是小量,而对于非环绕型航天器并无此限制,仅此而已。
有所不同,对于环绕型航天器,该项相对中心引力项是小量,而对于非环绕型航天器并无此限制,仅此而已。