




定轨,即轨道确定。一个最简单而直接的定义就是:根据对运动体(包括自然天体和各类航天器)的一列跟踪测量数据t
j
,Y
j
(j=1,2,···,k),用相应的数学方法确定其在某一历元t
0
时刻的运行状态X
0
。所谓t
0
时刻的运行状态X
0
,就是在选定的时空参考系中,运动体在t
0
时刻的位置和速度
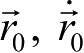 ,或该时刻的轨道根数σ
0
,如果是环绕型的天体(如人造地球卫星),即六个椭圆根数σ
0
=(a
0
,e
0
,i
0
,Ω
0
,ω
0
,M
0
)
T
。这6个椭圆根数的意义在前言中已说明,不再解释。关于历元t
0
,通常在测量弧段对应的时间区间[t
1
,···,t
k
]上或附近选取。
,或该时刻的轨道根数σ
0
,如果是环绕型的天体(如人造地球卫星),即六个椭圆根数σ
0
=(a
0
,e
0
,i
0
,Ω
0
,ω
0
,M
0
)
T
。这6个椭圆根数的意义在前言中已说明,不再解释。关于历元t
0
,通常在测量弧段对应的时间区间[t
1
,···,t
k
]上或附近选取。
定轨在天体力学或航天器轨道力学中通常有两个概念:短弧意义下的初轨确定和长弧(在特殊条件下也可以是短弧)意义下的轨道改进(现称为精密定轨)。对于初轨确定,传统意义下的定轨模型是对应一个无摄运动的二体问题。初轨确定无论在航天任务中,还是在太阳系各种小天体(小行星、自然卫星、彗星等)的发现过程中,都是不可缺少的工作。初轨本身可在某些问题中直接引用,或为精密定轨提供初始信息(即初值)。对于精密定轨,定轨模型则对应一个“完整”的力学系统,若是环绕型运动体(大行星、小行星和卫星)的定轨问题则为受摄二体问题,否则就是一般(n+1)体问题(其中 1 就是待定轨的运动天体——航天器)。精密定轨是根据大量观测资料所作的轨道确定工作,提供各种天体(自然天体和人造天体)的精密轨道。关于精密定轨,传统的称谓为轨道改进,但由于可以在定轨的同时确定某些参数(与待定轨的运动体轨道有关的一些几何和物理参数),此时待确定的状态量X
0
还包含这些参数,这就扩展了传统意义下单纯的轨道改进,故现称其为精密定轨——轨道确定与参数估计。另外,就精密定轨的原理和定轨的内容来看,尽管有改进轨道之意,但在定轨过程中必须提供的初始轨道
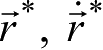 或σ
*
,仅仅起一个迭代初值的作用,它对应的时刻t
*
与定轨历元时刻t
0
并不需要一致,因此,轨道改进的称谓不如精密轨道确定(简称精密定轨)的称谓更恰当。
或σ
*
,仅仅起一个迭代初值的作用,它对应的时刻t
*
与定轨历元时刻t
0
并不需要一致,因此,轨道改进的称谓不如精密轨道确定(简称精密定轨)的称谓更恰当。
用以定轨的测量数据对应一种观测量,例如测距量ρ,测速量ρ˙,测角量α,δ(赤经、赤纬)和A,h (方位角和高度角)等。无论哪一类数据,习惯用符号Y表示,它们与定轨历元t 0 时刻运动体的状态量X 0 (指轨道量和待确定的某些几何、物理参数)有如下函数关系,即

此为测量方程,其中

实为运动体的状态转移方程,它是下列运动微分方程满足初始条件的解,即

关于方程的右函数F(X,t),如果仅就轨道状态量而言(即不提待估参数),就可以理解为该运动体所承受的各种外力引起的加速度。因此,一个完整的定轨问题,应该包含两个条件:一个是针对定轨对象的测量几何条件,即式(1.116);另一个是定轨对象运动所满足的动力学条件,即式(1.117),更确切地说就是需要提供上述运动微分方程的右函数F(X,t),这就涉及相应的动力学模型。
状态量X是n维,而一列观测量t j ,Y j (j=1,2,…,k)是m×k维,m≥1,m是观测量的维数(测距量一次采样是1维,而测角量一次采样则是2维)。当(m×k)≥n时,原则上方程组式(1.116)可解:由一列观测量t j ,Y j (j=1,2,…,k),给出历元t 0 时刻的状态量X 0 。但实质上它可归结为一个隐函数Φ(t,Y;t 0 ,X 0 )=0的求解问题,这将涉及解的确定性和如何求解问题,因此必须注意如下两点。
(1)解的确定性问题(定轨条件),即是否能由上述一列观测量t j ,Y j (j=1,2,…,k)唯一确定相应历元t 0 时刻的状态量X 0 ,亦称可观测性问题。例如卫星单站测距和测速,如果是短弧,将难以定轨,其具体的数学问题将在后面有关内容中阐明。
(2)如何求解问题,即在可定轨的前提下,上述定轨问题归结为一个多变元的非线性方程,无法直接求解,通常只能通过多变元迭代过程才能实现定轨。但对于短弧情况,只有测距和测速类型资料时必须采用一般的多变元迭代方法求解,测角资料则不然,即使考虑完整的力学系统,亦能通过一个特殊而简单的迭代过程实现定轨,这正是短弧初轨确定方法与建立在多变元迭代基础上的精密定轨方法的重大差别。
根据上述定轨的提法和原理来看,无论是自然天体的定轨,还是各类航天器的定轨,甚至是任何一个具有一定运动规律的运动体的“定轨”,都必须具备两个条件:一个以测量方程式(1.116)体现的几何条件;另一个即以运动微分方程式(1.118)体现的动力学条件。也就是说,定轨的确切含义就是动力学定轨,相应的定轨方法就是动力学方法,简称动力法定轨。对于航天器的定轨问题,在动力学模型的处理上会遇到各种困难,往往无法提供每种外力源的物理机制和数学模型,特别是那些表面力(大气、光压及相应的热辐射等)或一些随机因素,那么相应的式(1.118)的右函数F(X,t)就无法完全确定。正是鉴于这一原因,在具体定轨方法上相继出现了一些改进,例如引进处理部分外力源的简化动力学模型,或直接采用硬件获得某种外力源产生的加速度(获得表面力的加速度计的应用),甚至直接通过测量手段提供航天器运动过程中的位置、速度及加速度等,由此出现了相应的简化动力学方法和运动学方法(或称几何法)。但必须指出:这些在一定条件下的定轨方法只是动力学定轨方法的简化处理,简化的主要对象是动力学模型(用某种数学处理方法提供经验模型来替代,或采用加速度计的硬件处理直接提供某些外力作用引起的加速度等),而不会改变定轨的动力学基本原理,因此,这些简化方法并不是与动力学定轨方法“并列”的另类新方法。更重要的是就定轨的根本目的而言,还是要通过定轨确定相应的动力学模型,即式(1.118)的右函数F (X,t),否则确定的不是一条真实的轨道,而仅仅是运动体在跟踪弧段内的一种高精度拟合状态。例如,重力卫星采用加速度计避开地球大气等无法精确确定模型的障碍,达到提高地球引力场模型精度的目的,但它还是不能解决低轨卫星轨道外推的精度问题。
航天器轨道运动的状态量X 满足运动微分方程(1.118),即常微初值问题。
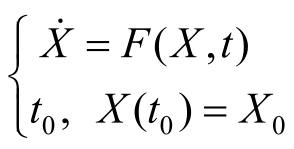
轨道预报问题的核心就是给出该状态微分方程满足初始条件X (t 0 )=X 0 的解,即

该表达形式可以是对应方程分析解的一个函数形式,也可以是对应方程数值解的一个离散形式。由t时刻的状态量X (t)可换算出所需要的与航天器位置有关的各几何量。
由运动微分方程及其解的获得清楚地表明,制约航天器轨道预报精度有如下三个方面:
(1)状态微分方程(1.118)的右函数,即力模型的真实性。
(2)初始条件X 0 的精度,这取决于前面所说的定轨的精度。
(3)求解方法能够达到的精度。
关于这三个方面,目前,计算方法完全可以达到高精度的要求,无论是理论方法还是实现计算的硬件条件,都不成问题。而前两个方面都与定轨不可分割,初始条件X 0 的精度就是定轨精度,而力模型亦是由定轨确定的。因此,提高轨道预报精度的关键同样是外力因素的准确建模问题,这显然又归结为完满解决定轨问题。