




火星探测器轨道涉及的空间坐标系,分为既各自独立又有一定联系的两个系统:一是环火星轨道问题涉及的火心坐标系统,二是探测器从地球发射涉及的地心坐标系统。与月球坐标系统类似,有历元火心天球坐标系、历元火心平赤道坐标系、火心黄道坐标系和火固坐标系。表1.7列出这些坐标系的坐标原点、参考平面(即XY平面)和X坐标轴方向。
表1.7 常用的火星坐标系(参考系)的定义
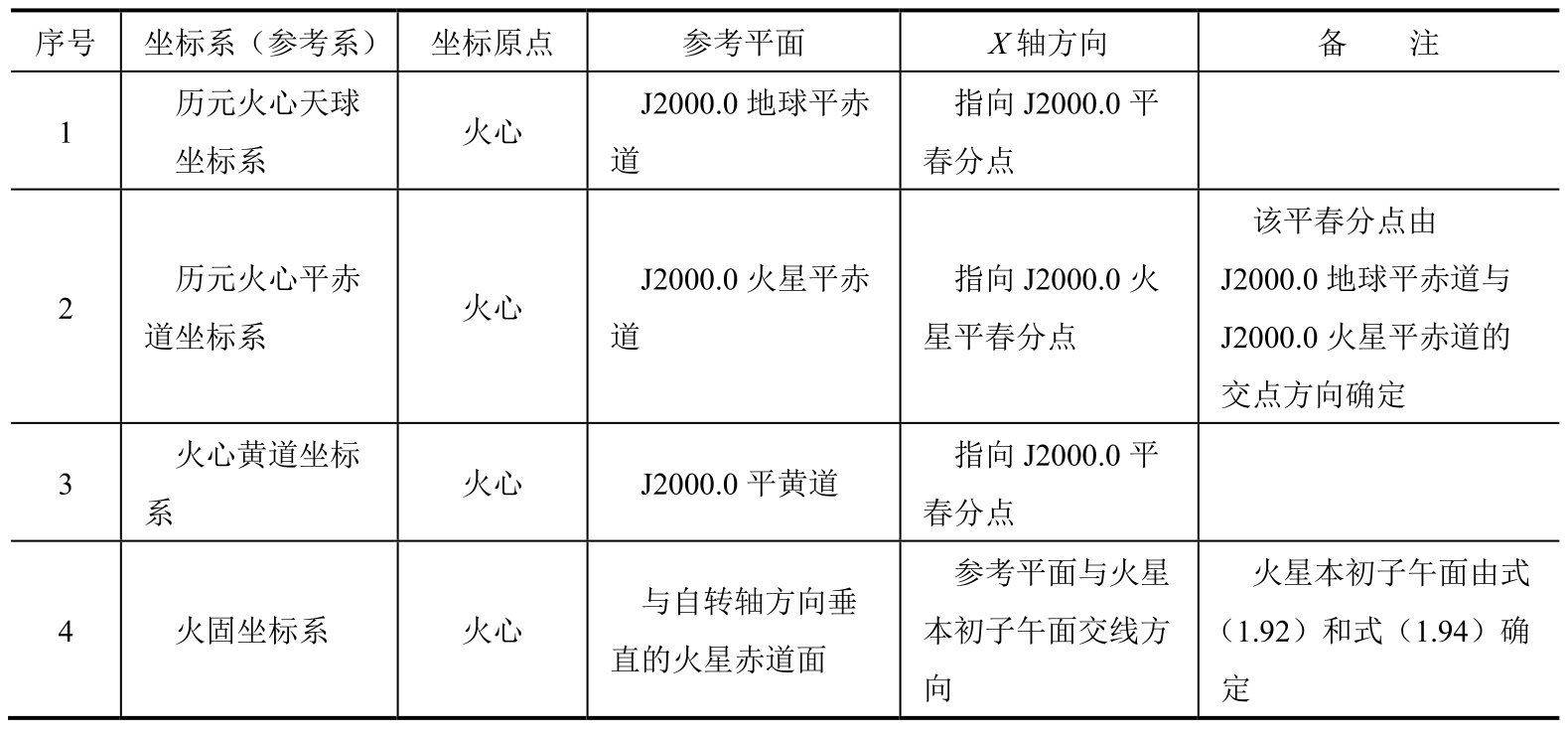
对于环火星探测器轨道问题,主要涉及 历元(J2000.0)火心赤道坐标系 和 火固坐标系 。关于火固坐标系,与地固坐标系类似,同样与火星引力位及探测器星下点在火星表面的位置等量有关,因此,它也对应一定的火星引力场模型。
关于火星坐标系统,与月球坐标系统中相应坐标系的引入类似,同样涉及地心坐标系与火心坐标系的相互联系问题。考虑到实用性,这里引用ⅠAU 2000天体(包括各大行星和月球等天体)定向模型 [14,15] 来确定基本坐标面,对火星而言,即火星定向模型,见图1.6。在ⅠAU 2000规范中分别定义了 历元(J2000.0)火心天球坐标系 和 火心赤道坐标系 ,前者的基本坐标面(xy坐标面)是 J2000.0 的地球平赤道面,第一方向(即x轴方向)仍就是相应的平春分点γ方向;而后者的基本坐标面则是 J2000.0 的火星平赤道面,相应的第一方向即ⅠAU 2000火星定向模型中的J2000.0地球平赤道与J2000.0火星平赤道的交点Q方向,该点就相当于火心赤道坐标系统中的“春分点”,见图1.6。尽管这一模型没有考虑章动效应,但火星章动量较小(最大项的摆幅约 1′′),对轨道的影响又无“累积”效应,对于一般问题无须考虑。既然不考虑章动,那么在下面的阐述中,除严格定义外,不再区分 真赤道面 和 平赤道面 ,或称平赤道面,或简称赤道面。正是由于ⅠAU 2000天体定向模型在相应天体的赤道面摆动上并没有详尽的考虑,如月球的物理天平动、火星自转轴的章动等,在1.3节月球坐标系统就未提及这一天体定向模型。
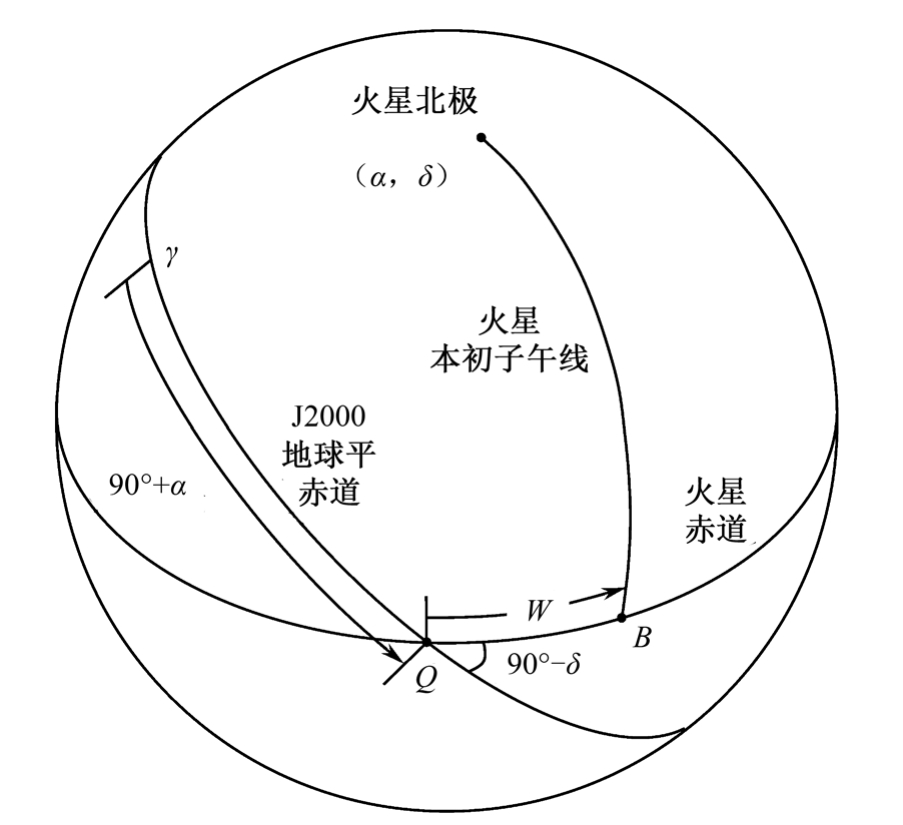
图1.6 ⅠAU火星定向模型
ⅠAU 2000 火星定向模型给出了因岁差原因火星平天极在火心天球坐标系中的赤经、赤纬计算公式为
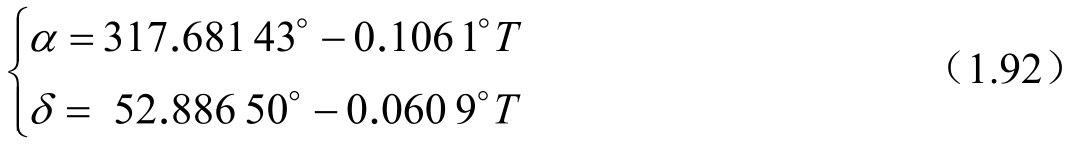
T即前面定义的自 J2000.0 起算的时刻 t 对应的儒略世纪数。式(1.92)表达的是类似地球平天极的长期(长周期)变化。对于J2000.0历元,有
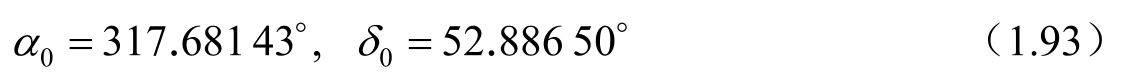
此为火星历元平极在火心天球坐标系中的指向。
在上述定义下,火星自转角将由图1.6中的W
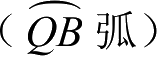 定义,即从Q点向东计量至B点(火星本初子午线方向,相当于火星上的格林尼治方向),可以将角度W看作火星上的格林尼治恒星时,由于没有考虑火星自转的章动效应,故不再区分真恒星时和平恒星时。ⅠAU 2000模型给出火星的自转矩阵,即
定义,即从Q点向东计量至B点(火星本初子午线方向,相当于火星上的格林尼治方向),可以将角度W看作火星上的格林尼治恒星时,由于没有考虑火星自转的章动效应,故不再区分真恒星时和平恒星时。ⅠAU 2000模型给出火星的自转矩阵,即
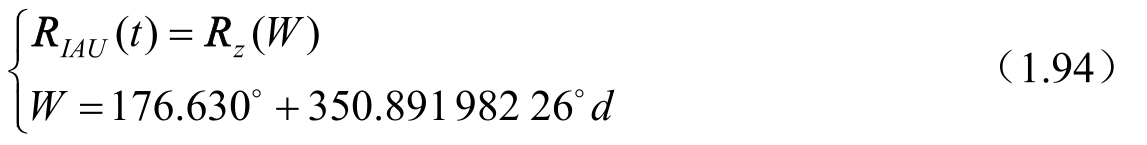
d为自J2000.0起算的儒略日。
上述选择容易与地球坐标系统相连,这对处理火星探测器的轨道问题(包括发射轨道和环火星运行轨道)及其他有关问题都很方便。同样,对于太阳系其他大天体的探测而言,亦可采用ⅠAU 2000天体定向模型来处理类似问题,相关数据详见本书附录D。
根据式(1.92)表达的ⅠAU 2000火星定向模型中火星平天极的变化规律,可以用图1.7来示意因岁差引起的火星平赤道面的变化状态。该图中的α 0 ,δ 0 为历元J2000.0时火星平极的赤经、赤纬,其值由式(1.93)给出。
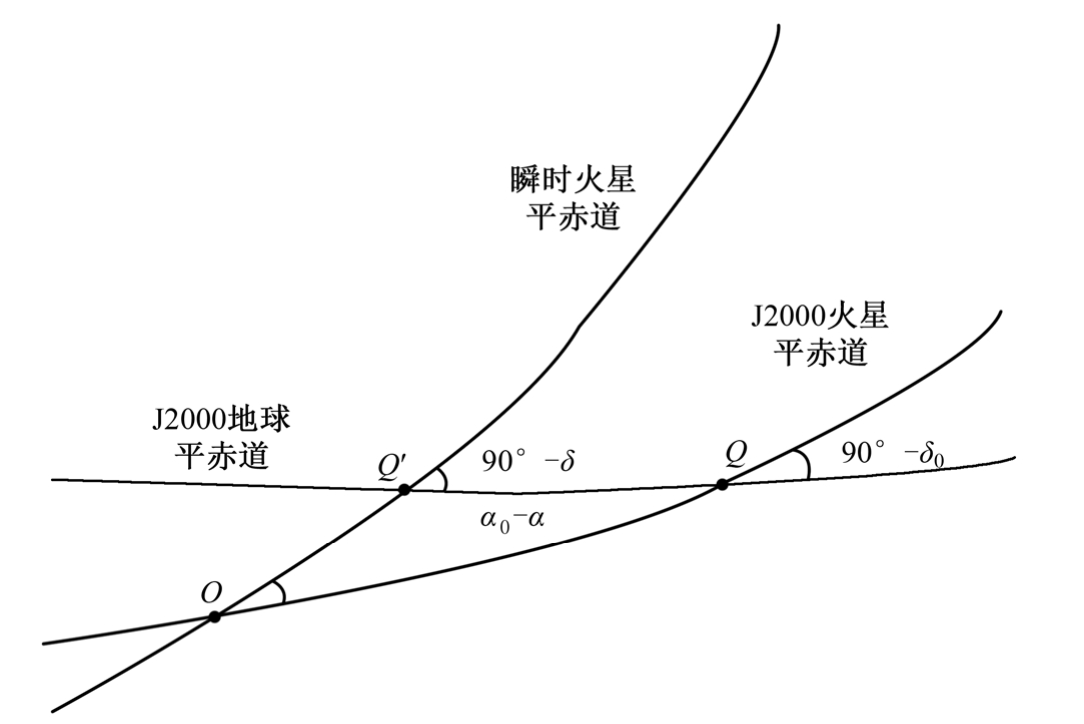
图1.7 ⅠAU2000火星定向模型给出的火星平赤道变化示意图
图1.7表达了J2000.0地球平赤道与J2000.0火星平赤道及瞬时火星平赤道之间的空间几何关系,而α,δ则为t时刻瞬时火星平极的赤经、赤纬,由式(1.92)表示。在此示意下,图1.7中的Q和Q′为火星坐标系统中的历元平春分点和瞬时平春分点。若分别用
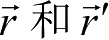 记作历元平赤道坐标系(火心赤道坐标系)和瞬时平赤道坐标系中同一探测器的位置矢量,它们之间的转换关系为
记作历元平赤道坐标系(火心赤道坐标系)和瞬时平赤道坐标系中同一探测器的位置矢量,它们之间的转换关系为

其中,坐标转换矩阵( PR )是火星的岁差矩阵,注意,该符号与地球的岁差矩阵相同,其具体形式为
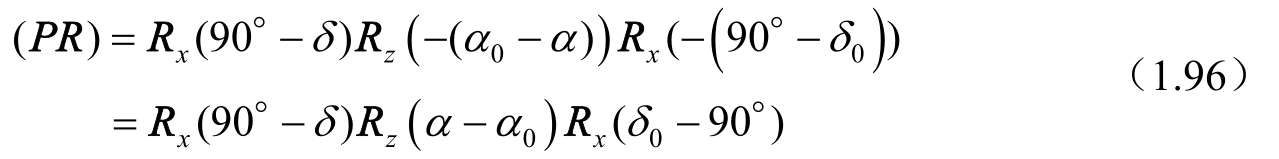
对于环火星探测器轨道问题,显然要涉及火心赤道坐标系与火固坐标系之间的转换关系。按照通常习惯,探测器的空间位置矢量在上述火心赤道坐标系和火固坐标系中分别记作
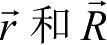 ,
那么在不考虑火星地极移动和天极章动的前提下,两个坐标系之间的转换关系为
,
那么在不考虑火星地极移动和天极章动的前提下,两个坐标系之间的转换关系为

其中,坐标转换矩阵( MP )只包含两个旋转矩阵,有

这里的旋转矩阵( MR )为火星自转矩阵:( MR )= R IAU (t)= R z (W),见式(1.94)。
涉及这两个系统之间坐标转换的物理量大致包含两类:探测器的位置和速度矢量、太阳与大行星的位置矢量。在建立转换关系中将要涉及地球和火星的日心黄道坐标矢量,记为
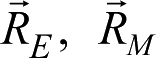 ,对于高精度问题,可引用JPL历表(如DE405),而对一般问题则可采用简单的分析历表。关于分析历表,可由相应的平均轨道给出,这里与地球的平均轨道根数一并列出。
,对于高精度问题,可引用JPL历表(如DE405),而对一般问题则可采用简单的分析历表。关于分析历表,可由相应的平均轨道给出,这里与地球的平均轨道根数一并列出。
地球在J2000.0日心黄道坐标系中的平均轨道根数
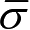 为
为

火星在J2000.0日心黄道坐标系中的平均轨道根数
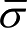 为
为

式(1.99)和式(1.100)中的T和d前面已定义过,即自J2000.0起算的时刻t对应的儒略世纪数和儒略日。由轨道根数转换成位置矢量和速度矢量的运算:
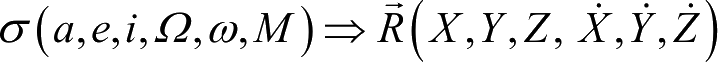 是一个常识性的问题,这里不再具体列出。
是一个常识性的问题,这里不再具体列出。
在火星探测的轨道问题中,将会涉及地心坐标系与火心坐标系之间的两类转换关系,下面具体介绍。
地固坐标系、地心天球坐标系、火固坐标系和火心赤道坐标系中探测器的位置矢量分别记为
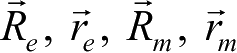 ,速度矢量为
,速度矢量为
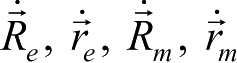 ,探测器在两个星固坐标系中的位置矢量
,探测器在两个星固坐标系中的位置矢量
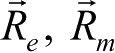 不要与地球和火星的日心位置矢量
不要与地球和火星的日心位置矢量
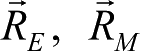 相混淆。
相混淆。
具体需要的是探测器的位置矢量由地心坐标系到火心坐标系的转换:
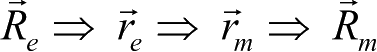 ,或其逆转换:
,或其逆转换:
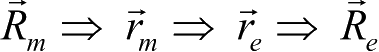 。
。
地心坐标系到火心坐标系的转换
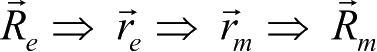 ,按下列过程进行,即
,按下列过程进行,即
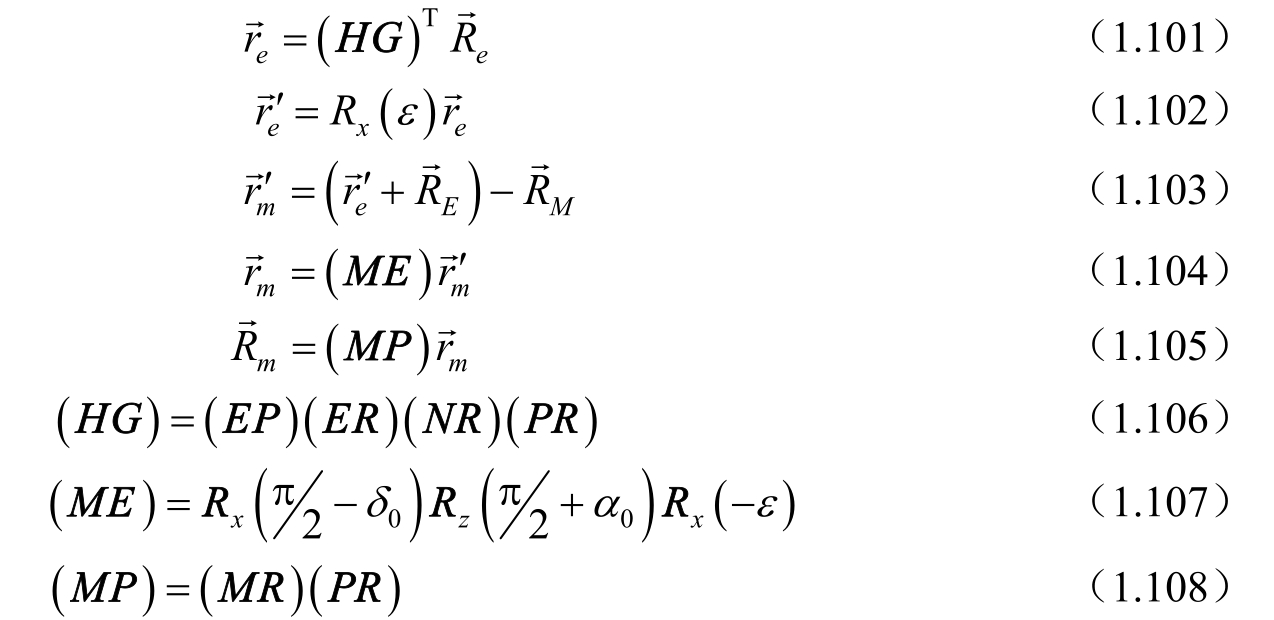
其中,转换矩阵(
H G
)为前面已给出的式(1.30),或式(1.75);转换矩阵(
M E
)中出现的α
0
,δ
0
由式(1.93)给出,即历元 J2000.0 时刻火星平天极在火心天球坐标系中的赤经、赤纬(见图1.6),ε是历元J2000.0时刻的平黄赤交角,由式(1.63)给出;而构成转换矩阵(
MP
)的火星岁差矩阵(
PR
)和自转矩阵(
MR
)=
R
z
(W),分别见式(1.96)和式(1.94)。
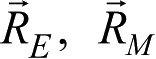 前面已有说明,即日心黄道坐标系中的地球和火星的位置矢量。
前面已有说明,即日心黄道坐标系中的地球和火星的位置矢量。
火心坐标系到地心坐标系的转换
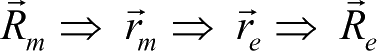 ,即上述转换的逆过程,按下列过程进行,即
,即上述转换的逆过程,按下列过程进行,即

其中涉及的转换矩阵均已在前面列出。
在环火星轨道问题中会涉及太阳、大行星(以地球为代表)和火星的两颗自然卫星的摄动影响,这就需要提供这些天体在火心赤道坐标系中的位置矢量。关于火星的两颗自然卫星(Phobos 和 Deimos),其轨道本身就是在火心天球坐标系中建立的,无须再讨论。下面列出太阳和地球的位置矢量在火心赤道坐标系中的表达形式,该坐标系中太阳和地球的位置矢量分别记为
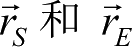 ,有
,有

关于探测器和各天体的速度矢量在不同坐标系之间的转换,不再具体列出,但要指明一点:由于岁差、章动等量的变率都很小,相应的转换矩阵均可当作常数矩阵处理,在速度矢量转换过程中只有地球和火星的自转矩阵需要考虑其变化,变化率为它们各自的自转角速度。