下载掌阅APP，畅读海量书库
立即打开
就月球探测器的运动而言，将涉及四个月球坐标系，即历元月心天球坐标系、历元月心平赤道坐标系、月心黄道坐标系和月固坐标系。表1.6列出这些坐标系的坐标原点、参考平面（即XY平面）和X坐标轴方向。
表1.6 常用的月球坐标系（或参考系）的定义
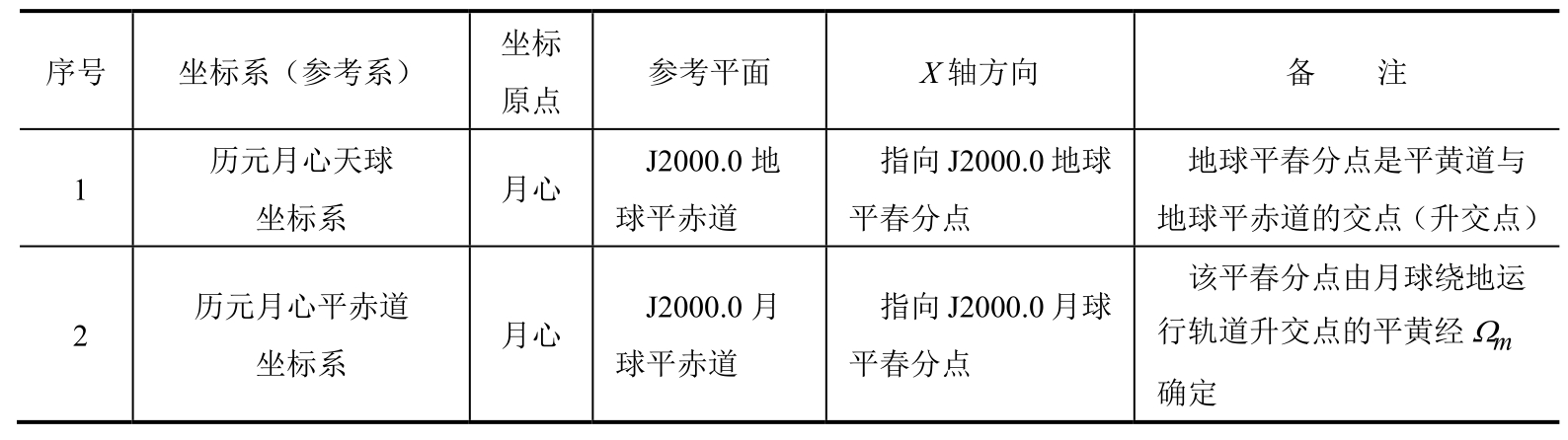
（续表）
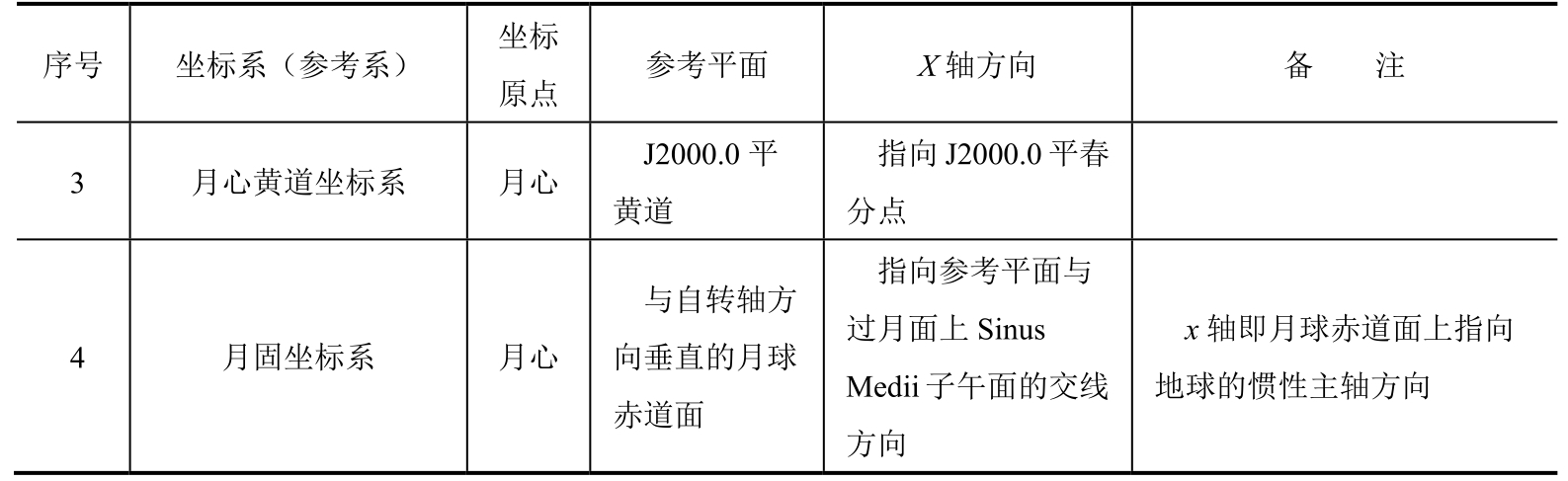
与地球赤道面在空间的摆动类似，月球赤道面亦有此摆动现象，即物理天平动，它同样引起月心赤道坐标系的各种不同定义，这将涉及环月卫星运动的轨道确定和星下点（即卫星与月心连线在月球表面的交点）位置的确定。
这里所说的月心天球坐标系（见表1.6），就可以简单地理解为仅仅将地心天球坐标系的坐标原点平移至月心，该坐标系的参考平面（即XY平面）和X坐标轴方向仍然是地心天球坐标系的选择，这便于地球坐标系统与月球坐标系统进行关联。对于其他大天体的天球坐标系也是这样引入的，详见本书附录D，后面在火星坐标系统中会有进一步的阐述。
目前采用的即J2000.0月心平赤道坐标系，该坐标系的原点是月心，xy坐标面就是J2000.0月球平赤道面，x轴方向是该赤道面上的平春分点
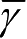方向，这一方向由月球绕地运行轨道升交点的平黄经Ω
m
确定，见图1.4。与处理地球卫星轨道问题类似，这是处理环月探测器轨道问题中必须采用的坐标系，但为了区别上述J2000.0月心天球坐标系，称其为J2000.0月心平赤道坐标系，或简称J2000.0月心赤道坐标系。与地心天球坐标系类似，也是一个在一定意义下（即消除了坐标轴因月球赤道面摆动引起的转动）的月心“不变”的坐标系，它可以在同一个坐标系中来表达不同时刻的探测器轨道。同样，在该坐标系中，月球非球形部分的引力位也是变化的。
该坐标系的原点O仍是月心，和地心黄道坐标系只是一个平移关系。x′y′坐标面是历元（J2000.0）时刻的黄道面，x′轴方向与上述天球坐标系（O-xyz）的指向一致，即该历元的平春分点方向。
坐标原点O是月心，而Z轴方向是月球的自转轴方向，XY坐标面即过月心并与自转轴方向垂直的月球赤道面，X轴指向月球上的“格林尼治”子午线方向：基本平面（XY坐标面）与过月面上Sinus Medii子午面的交线方向，即月球赤道面上那一指向地球的惯性主轴方向。显然，在这种坐标系中，相应的月球引力位亦是确定的，各种月球引力场模型及其参考椭球体也都是在这种坐标系中给定的，它们同样应该是一个自洽系统。
月球的物理天平动同样是一个定点转动问题。与地球自转的岁差章动类似，多年来的研究曾先后给出过多种有关物理天平动的理论，几乎都以物理天平动的经度分量、倾角分量和节点分量（τ，ρ，σ）的分析解来表达，这三个量就将月球的平赤道与真赤道以分析形式相联系。
对于平赤道，根据Cassini定律，月球轨道、黄道与月球平赤道交于一点
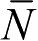。由于月球天平动的原因，月球真赤道将通过（τ，ρ，σ）三个量在空间与平赤道联系起来，见图1.4。图中各量的关系如下，即
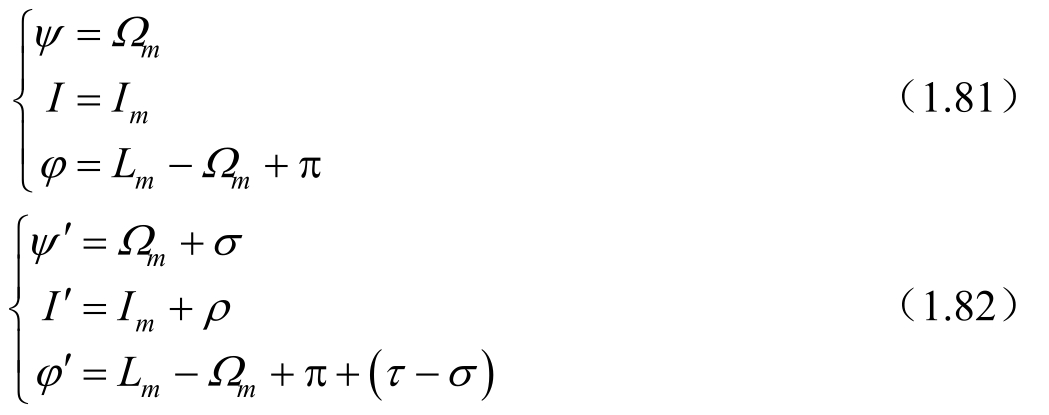
其中，I m ，Ω m ，L m 分别为月球平黄赤交角、轨道升交点平黄经和月球平黄经。
美国喷气推进实验室（JPL）的数值历表（如DE405）却以另一种形式表达了月球物理天平动，它是直接给出另三个欧拉角（Ω′，i s ，Λ）每天的具体数值（见图1.5），可用于计算月球卫星在月固坐标系中的精确位置。
上述两种物理天平动的表达形式，可通过图1.5来表明它们之间的关系。图1.5中x b 是月固坐标系的X轴指向，即图1.4中的ξ′方向。三个欧拉角（Ω′，i s ，Λ）在图中已表示清楚，不再加以说明，ε是地球的平黄赤交角。
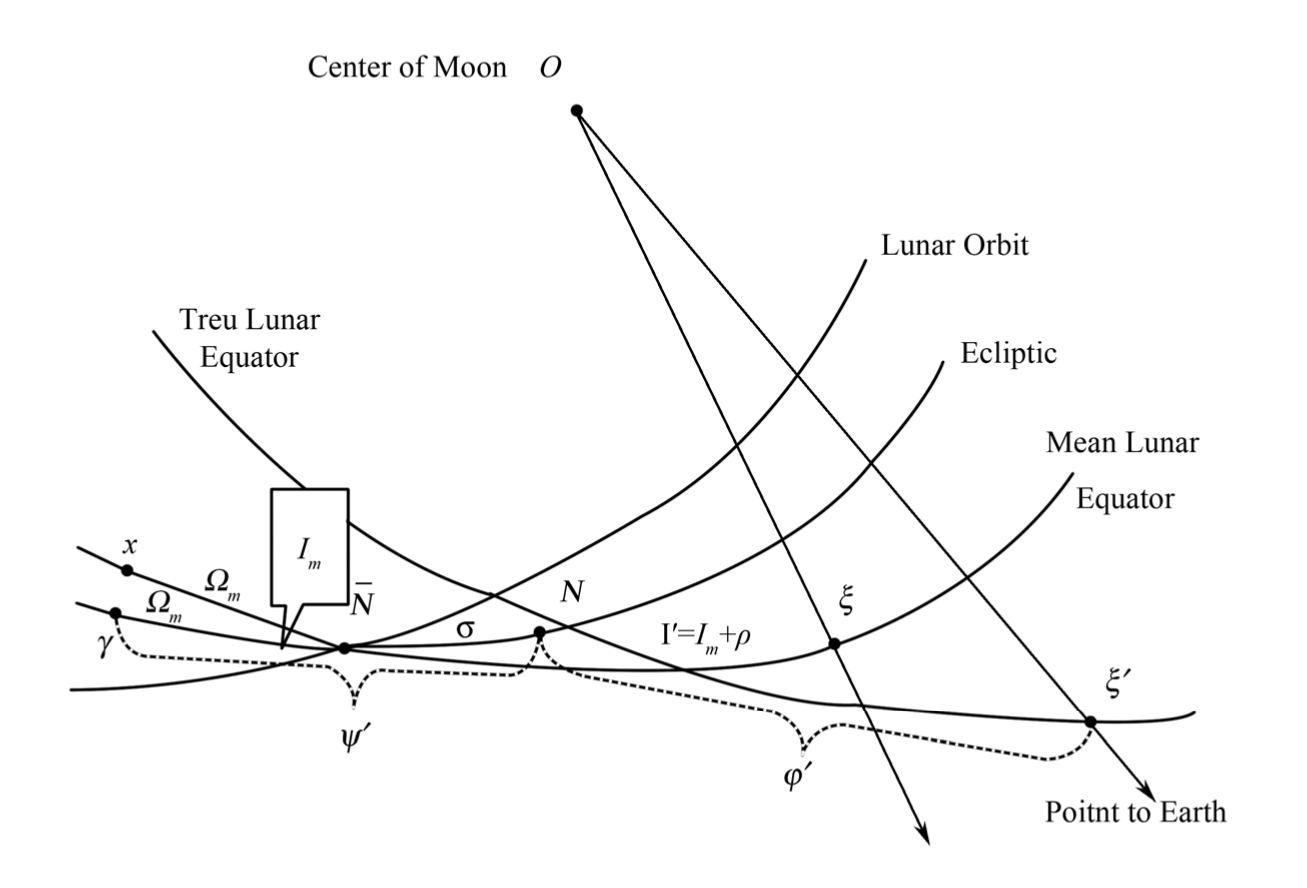
图1.4 月球真赤道与月球平赤道之间的关系
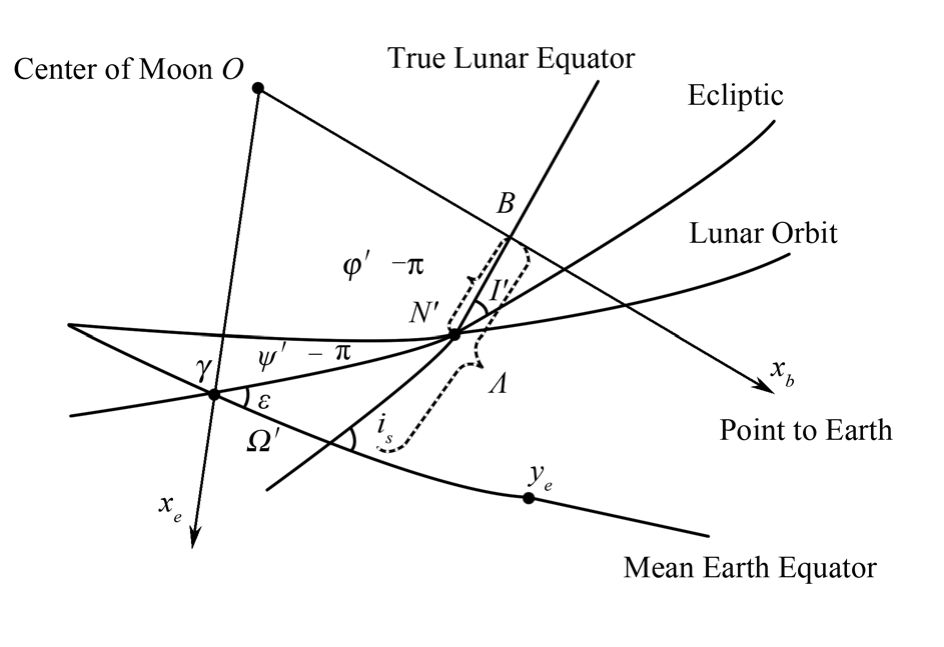
图1.5 月心坐标系与物理天平动示意图
根据月球自转理论，给出的物理天平动三个参数（τ，ρ，σ）的分析表达式，类似于地球的章动序列，亦包含几百项，最大的周期项振幅超过100′′（100 角秒），但没有地球赤道摆动中的长周期项（即周期近26 000年的岁差项）。月球自转理论越来越精确，给出的分析表达式与 DE405 高精度数值历表也越来越接近，相差不到1′′。但若精度要求高，分析表达式取项则太多，不便于应用，而数值历表似乎简捷易用，但它不便于分析某些问题。在不同问题中可采用不同的表达形式：分析解（τ，ρ，σ）或数值历表（Ω′，i s ，Λ）。通过两者的比较证实：在涉及弧段不太长（1～2天或更长些）的情况下，对于探测器定轨或预报，无论是采用数值法还是分析法，涉及物理天平动问题，均可用下面给出的Eckhardt分析解的前四项的简化表达式，具体参见式（1.83）。
首先列出Eckhardt表达式（τ，ρ，σ）的前几项 [12] ，作为与数值历表（Ω′，，i s ，Λ）的比对依据，形式如下，即
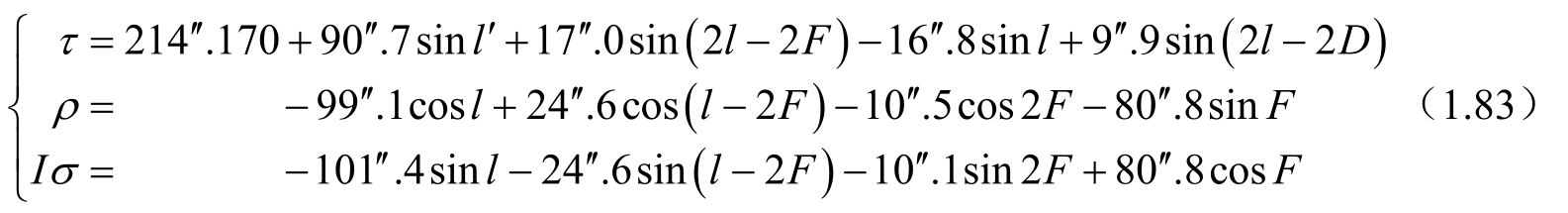
式（1.83）中，τ包含了自由项214′′.170；I=1 ° .542 461=5 552′′.86，即式（1.81）中已出现过的月球的平黄赤交角；l，l′，F和D各为月球的平近点角、太阳的平近点角、月球的平升交点角距（即F=l+ω m ，ω m 是月球轨道的近地点幅角）和日月平角距。它们的计算公式分别为
其中，角度F和D在前面地球坐标系涉及的计算公式中出现过，具体参见式（1.55）和（1.56）。
下面把（τ，ρ，σ）的分析表达式[见式（1.83）]与DE405数值历表值（Ω′，i
s
，Λ）通过坐标转换来进行比较。（Ω′，i
s
，Λ）涉及月心天球坐标系（O-x
e
y
e
z
e
），这里所说的月心天球坐标系中，x
e
y
e
坐标面即前面定义的J2000地球平赤道面，为了区别起见，在该坐标系中的坐标矢量记为
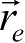。月固坐标系（O-XYZ，即图 1.4 中的O-ξ′η′ζ′）中相应的坐标矢量记为
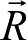。对这两种坐标系，分别采用上述两种天平动表达形式（数值和分析）建立坐标转换关系，有
其中两个转换关系分别由以下两式表达，即
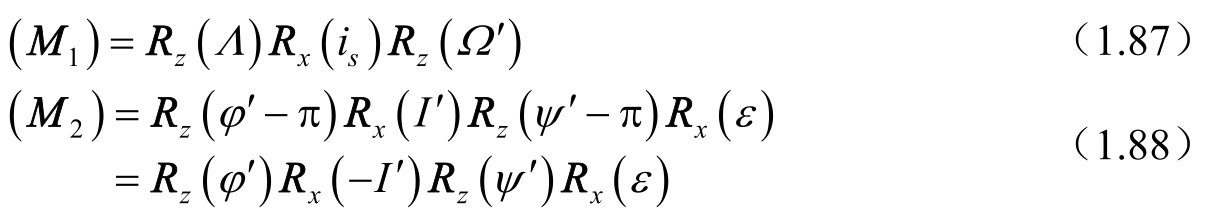
式（1.88）第一行是按图 1.5 给出的，而第二行是按图 1.4 给出的，两者实为同一转换关系。式（1.87）和式（1.88）分别给出的两种转换矩阵之间的差别，取决于（τ，ρ，σ）取项的多少，如果像式（1.83）那样只取完整表达式中的前几个主项，将月球表面一点的空间坐标转换到月固坐标系中的位置，两种转换之差可达公里级，相应的转换矩阵元素的最大差别达到10 -3 。
根据上述比较可知，直接采用分析解的简化表达式，在某些问题中是不能满足精度要求的。但在考虑物理天平动对环月探测器轨道的影响时，在一定精度要求的前提下，则无妨，因为它是通过非球形引力位（最大的J 2 项仅为10 -4 的量级）来体现的。定轨或预报中涉及轨道外推弧段为10 2 时（对低轨探测器为1～2天的间隔），要保证10米级甚至米级精度，采用Eckhardt的前四项表达形式[见式（1.83）]是可以达到的。因此，具体采用哪一种转换关系应根据不同问题的具体要求而选择。
鉴于上述比较结果，要建立月球卫星轨道理论，了解轨道变化的规律，或直接反映月球卫星相对月心坐标系的几何状况，必须采用月心赤道坐标系，而不是月心地球赤道坐标系（即前面定义的J2000月心天球坐标系）。那么用（τ，ρ，σ）的分析表达式来建立历元月心平赤道坐标系（O-xyz）与月固坐标系（对应真赤道，O-ξ′η′ζ′）之间的转换关系，显然是有必要的。而若要通过月心平赤道坐标系（O-xyz）与月心天球坐标系（O-x
e
y
e
z
e
）之间的转换关系（即利用高精度的Ω′，i
s
，Λ值）来计算月球卫星在月固坐标系中的精确位置
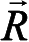也很简单，有
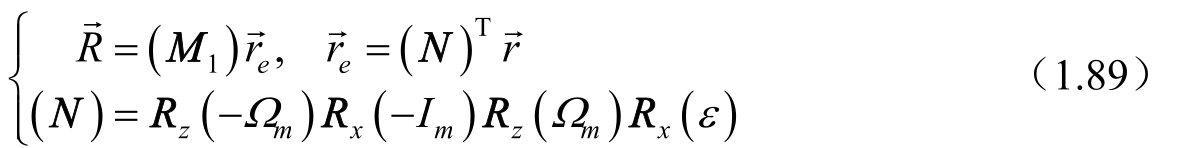
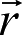是通过定轨或预报给出的月心平赤道坐标系中的月球卫星位置矢量。这里变换矩阵（
N
）并不涉及物理天平动的表达形式，转换的精度只取决于月球卫星定轨或预报的精度。
对于月球卫星的运动，要构造相应的轨道分析解，可以在历元月心平赤道坐标系中考虑问题。该坐标系的xy坐标面即J 2000.0平赤道面，x轴方向即相应的平春分点方向，由月球轨道升交点的平黄经Ω m 确定。在分析法定轨和数值法定轨及预报中均采用这种统一坐标系，只需要将相应的由物理天平动引起的坐标系附加摄动给出即可，而这种附加摄动并不复杂，作者已经具体给出，见《卫星轨道理论与应用》 [10] 一书的第5章。
分别记月心赤道坐标系（即历元月心平赤道坐标系，O-xyz）和月固坐标系（对应真赤道，O-ξ′η′ζ′）中月球卫星的坐标矢量为
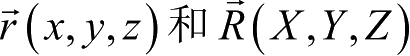，两者之间的转换关系为
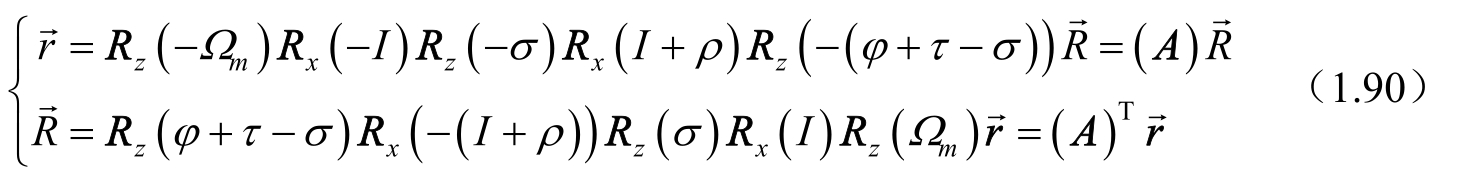
其中， R z （-Ω m ）， R x （-I）， R z （-σ）， R x （I+ρ）， R z （-（φ+τ-σ））是正交矩阵。
由于目前对月球探测器的测控都是由地面测控站来完成的，这就涉及历元地心天球坐标系，同时出现了历元月心天球坐标系和历元月心赤道坐标系。它们之间的转换，会涉及月球的地心坐标。这同样可由两种途径获得：一种是高精度的数值历表（如JPL的DE系列历表），另一种即精度较低的分析历表。在J2000.0地心黄道坐标系中月球的平均轨道根数
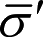由下式表达，即
式中，t和d分别为由标准历元 J2000.0 起算的世纪数和儒略日，定义在前面已介绍过。由于其轨道摄动变化较大，最大的周期项振幅可达2×10 -2 ，故式（1.92）的精度较低。至于在具体定轨工作中，对月球坐标采用高精度的数值历表还是简单的分析历表，这将取决于对定轨精度和计算效率的不同要求。