




除前面介绍的国际天球参考系(ⅠCRS)、地心天球参考系(GCRS)和国际地球参考系(ⅠTRS)外,根据目前地球卫星的应用、地-月系探测及深空探测的现状,航天领域中涉及的地球参考系还有如下:
· 黄道坐标系;
· 站心地平坐标系;
· RTN地心轨道平面坐标系。
本章1.1节已说明在实际工作中参考系与坐标系两名称混用的原因,故下面不再重复说明。
依据坐标系定义的三大要素:坐标原点、参考平面(即XY平面)和X轴方向,表1.2列出航天领域中有关地球的常用坐标系(或参考系)。
表1.2 常用坐标系(或参考系)的定义
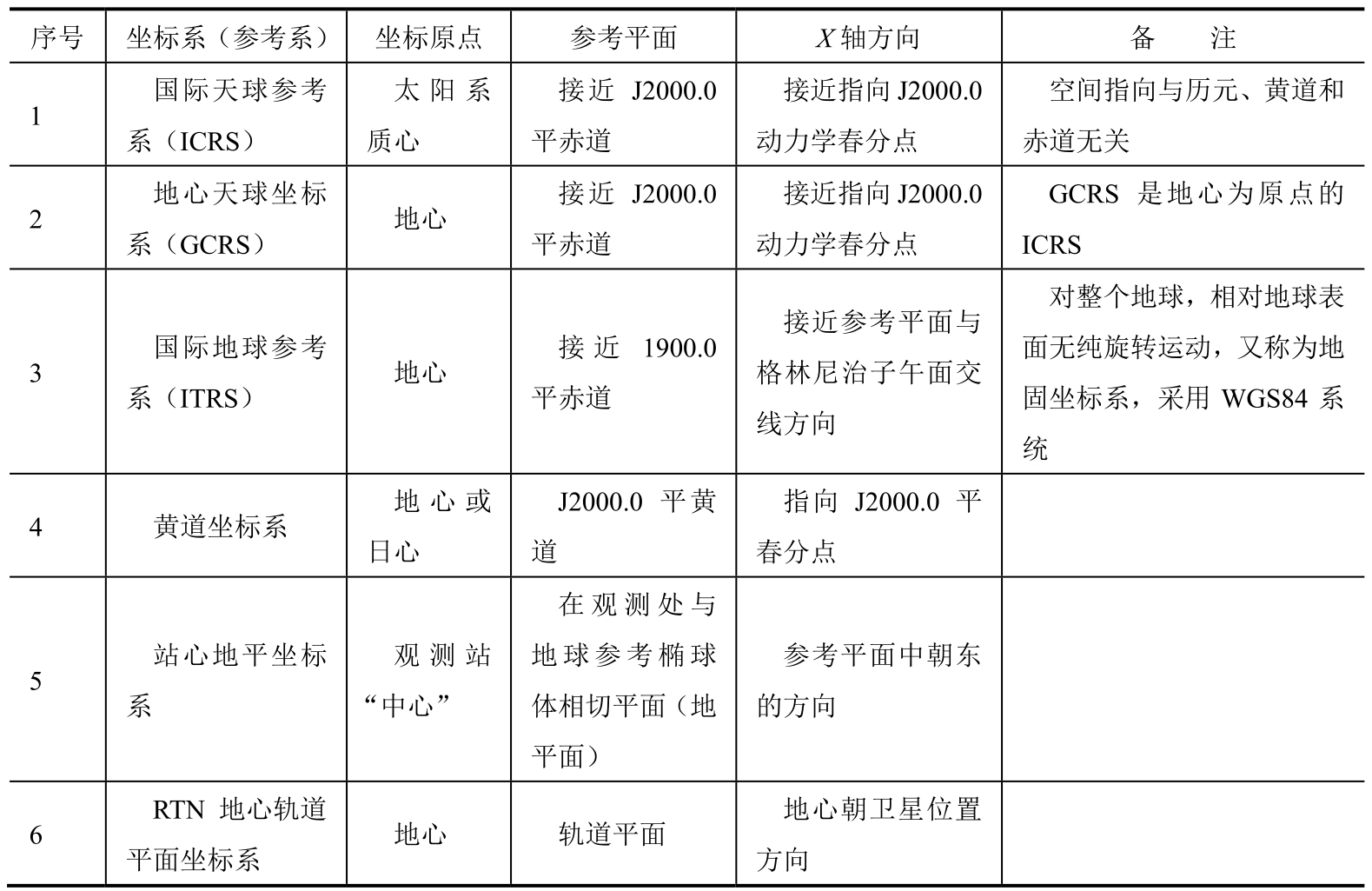
对于地球卫星,所涉及的主要是地心天球坐标系和地固坐标系,其坐标原点都是地心。但参考平面及其主方向的选择,将会受到岁差章动和地极移动的影响,而空间坐标系的复杂性正是由岁差章动和地极移动等原因引起的。日、月和大行星对地球非球形部分的吸引,会产生两种效应:一是作为刚体平动的力效应,将引起一种地球扁率间接摄动;另一种就是作为刚体定点转动的力矩效应,使地球像陀螺那样,出现进动与岁差章动(即自转轴在空间的摆动)。由于岁差章动引起的地球赤道面随时间在空间的摆动及由地球内部和表面物质运动引起的地球自转轴在其内部的移动(极移),都将影响坐标系中参考平面的选取。
考虑到知识的延续性和实用性,在不影响精度的前提下,本书将不完全拘泥于ⅠAU新规范“严格”定义的书面表达,如在各坐标系的定义和相互转换的一些细节方面,但给出的转换关系符合新规范,且满足精度要求。
此坐标系现为历元(J2000.0)地心天球坐标系,即前面已作了说明的J2000.0平赤道坐标系,简称地心天球坐标系。其坐标原点 O 是地心,xy 坐标面接近历元(J2000.0)时刻的平赤道面,x轴接近指向该历元的平春分点
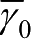 ,这是一个在一定意义下(即消除了坐标轴因地球赤道面摆动引起的转动)的“不变”坐标系,它可以将不同时刻运动天体(如地球卫星)轨道放在同一个坐标系中来表达,便于比较和体现天体轨道的实际变化,已是国内外习惯采用的空间坐标系。
,这是一个在一定意义下(即消除了坐标轴因地球赤道面摆动引起的转动)的“不变”坐标系,它可以将不同时刻运动天体(如地球卫星)轨道放在同一个坐标系中来表达,便于比较和体现天体轨道的实际变化,已是国内外习惯采用的空间坐标系。
注意:在该坐标中,地球非球形部分的引力位是变化的,这一变化将会引起所谓的地球卫星轨道变化的坐标系的附加摄动 [5~9] 。为了“避开”这一表面上的“麻烦”,曾在20世纪60年代引入了一种混合坐标系,亦称为“轨道坐标系”:xy坐标面改用瞬时真赤道面,而x轴则采用 J1950.0 平春分点,现在是 J2000.0 平春分点,美国相关领域为瞬时t平春分点。该坐标系的引入却真正带来了麻烦,即坐标系的多种转换及其连带问题,这在本系列专著“航天器轨道力学理论与工程应用”第二本——《卫星轨道理论与应用》(刘林、汤靖师著) [10] 中有详细阐述,并建议不必再引入该坐标系,简单给出相应坐标系附加摄动即可。在处理月球、火星等轨道问题中有这类问题,下面不再提及。
该坐标系即国际地球参考系(ⅠTRS),是一个跟随地球自转一起旋转的空间参考系,习惯称其为地固坐标系。在这个坐标系中,与地球固体表面连接的测站的位置坐标几乎不随时间改变,仅仅由于构造或潮汐变形等地球物理效应而有很小的变化。
地固坐标 系 的原点O是地心,XY 坐标面接近 1900.0 平赤道面,X轴指向接近参考平面与格林尼治子午面交线方向,即本初子午线方向,亦可称其为格林尼治子午线方向。各种地球引力场模型及其参考椭球体也都是在这种坐标系中确定的,它们应该是一个自洽系统。这里必须说明一点,在新的地固坐标系定义中,原国际习用原点(Conventional Ⅰnternational Origin,CⅠO)已弃用,现在的天球中间参考系和地球中间参考系的Z轴方向均为CⅠP(CelestialⅠntermediate Pole)。
根据我国的目前状况,如不加说明,所涉及的地固坐标系均采用WGS(World Geodetic System)84系统。对于该系统,有
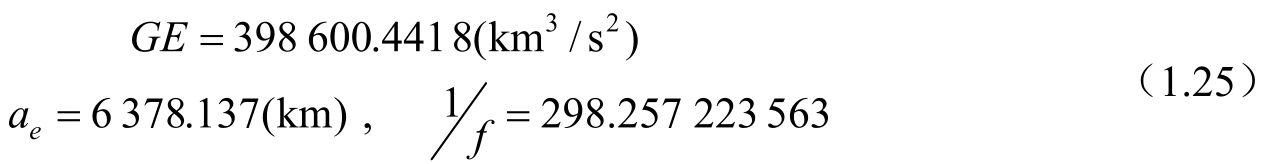
其中,GE是地心引力常数,a e 是参考椭球体的赤道半径,f 是该参考椭球体的几何扁率。
在地固坐标系中,测站坐标矢量
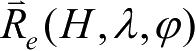 的三个直角坐标分量X
e
,Y
e
,Z
e
与球坐标分量(H,λ,φ)之间的关系为
的三个直角坐标分量X
e
,Y
e
,Z
e
与球坐标分量(H,λ,φ)之间的关系为
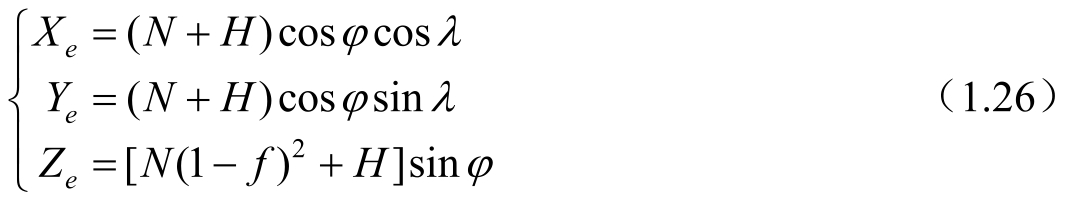
其中
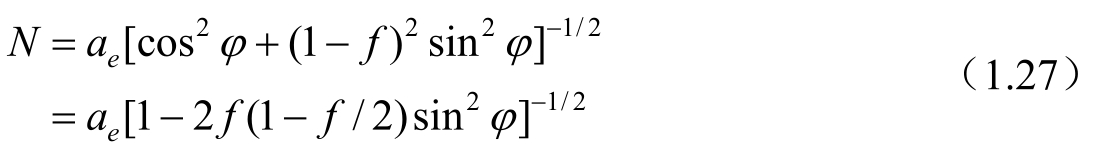
a e 是相应的参考椭球体的赤道半径,f 是该参考椭球体的几何扁率。球坐标的三个分量(H,λ,φ)分别为测站的大地高、大地经度和大地纬度(亦称测地纬度),有
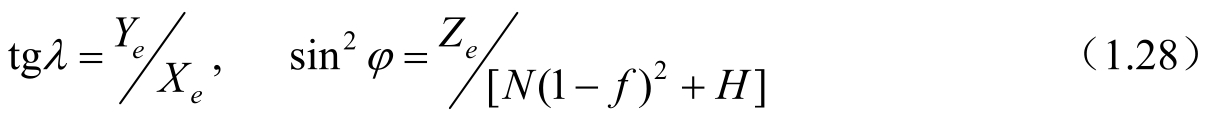
该坐标系的原点O仍是地心,和日心黄道坐标系只是一个平移关系。x′y′坐标面是历元(J2000.0)时刻的黄道面,x′轴方向与上述天球坐标系O-xyz的指向一致,即该历元的平春分点方向。
分别用
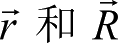 表示探测器在地心天球坐标系(O-xyz)和地固坐标系(O-XYZ)中的位置矢量。探测器的位置矢量在这两个坐标系之间的转换关系为
表示探测器在地心天球坐标系(O-xyz)和地固坐标系(O-XYZ)中的位置矢量。探测器的位置矢量在这两个坐标系之间的转换关系为

其中,坐标转换矩阵( HG )包含了四个旋转矩阵,有
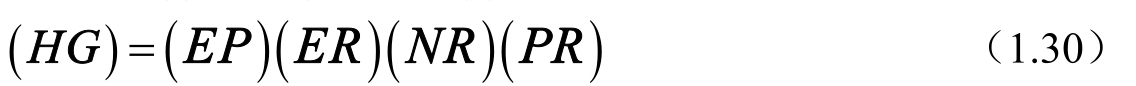
( PR )是岁差矩阵,( NR )是章动矩阵,( ER )是地球自转矩阵,( EP )是地球极移矩阵。它们分别可由下列各式表示
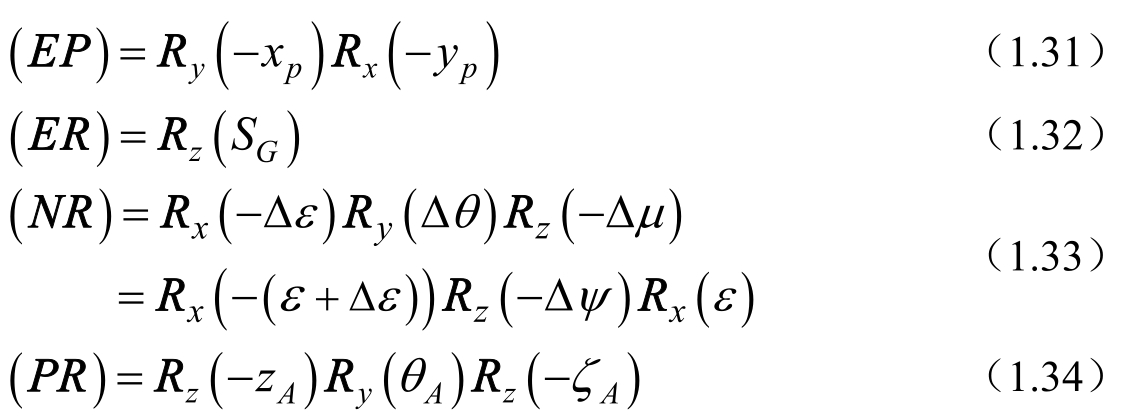
式(1.31)中的x p ,y p 是极移分量;式(1.32)中的格林尼治恒星时S G 为

μ和Δμ是赤经岁差和章动,J2000.0系统中的格林尼治平恒星时
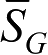 为
为
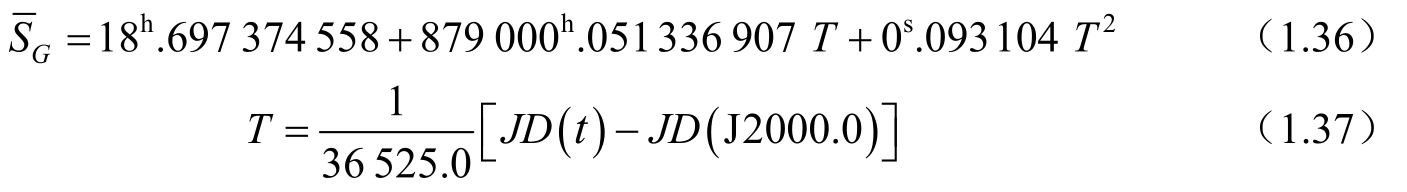
式中,t是UT1时间,但计算其他天文量(岁差章动等)时,t则为TDT时间。
式(1.34)中的岁差常数ζ A ,z A 和θ A 的计算公式为

θ A 是赤纬岁差,相应的赤经岁差μ(或记作m A )为
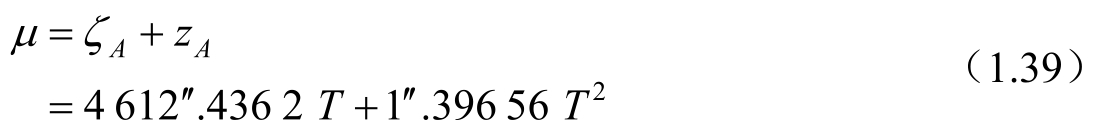
式(1.33)中的ε是平黄赤交角。ⅠAU(1980)章动序列给出的黄经章动Δψ和交角章动Δε的计算公式,包括振幅大于0′′.000 1的106项。考虑到一般问题涉及的轨道精度要求,只取振幅大于0′′.005的前 20 项(按大小排列)即可,由于是周期项(最快的是月球运动周期项),没有累积效应,故小于0′′.005的项引起的误差只相当于地面定位误差为米级,对于时间而言的差别小于0 s .001。取前20项的公式为
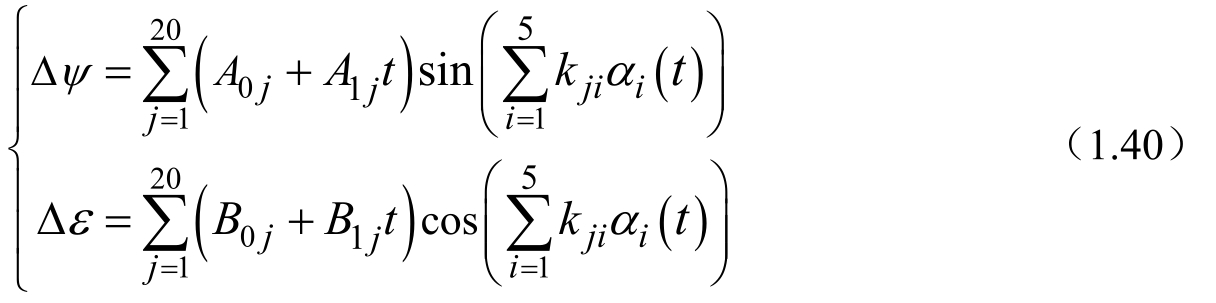
相应的赤经和赤纬章动Δμ和Δθ为

其中,平黄赤交角的计算公式为
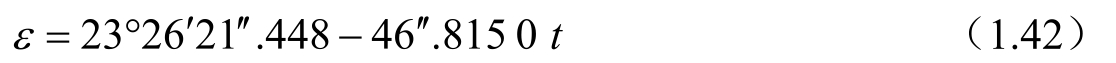
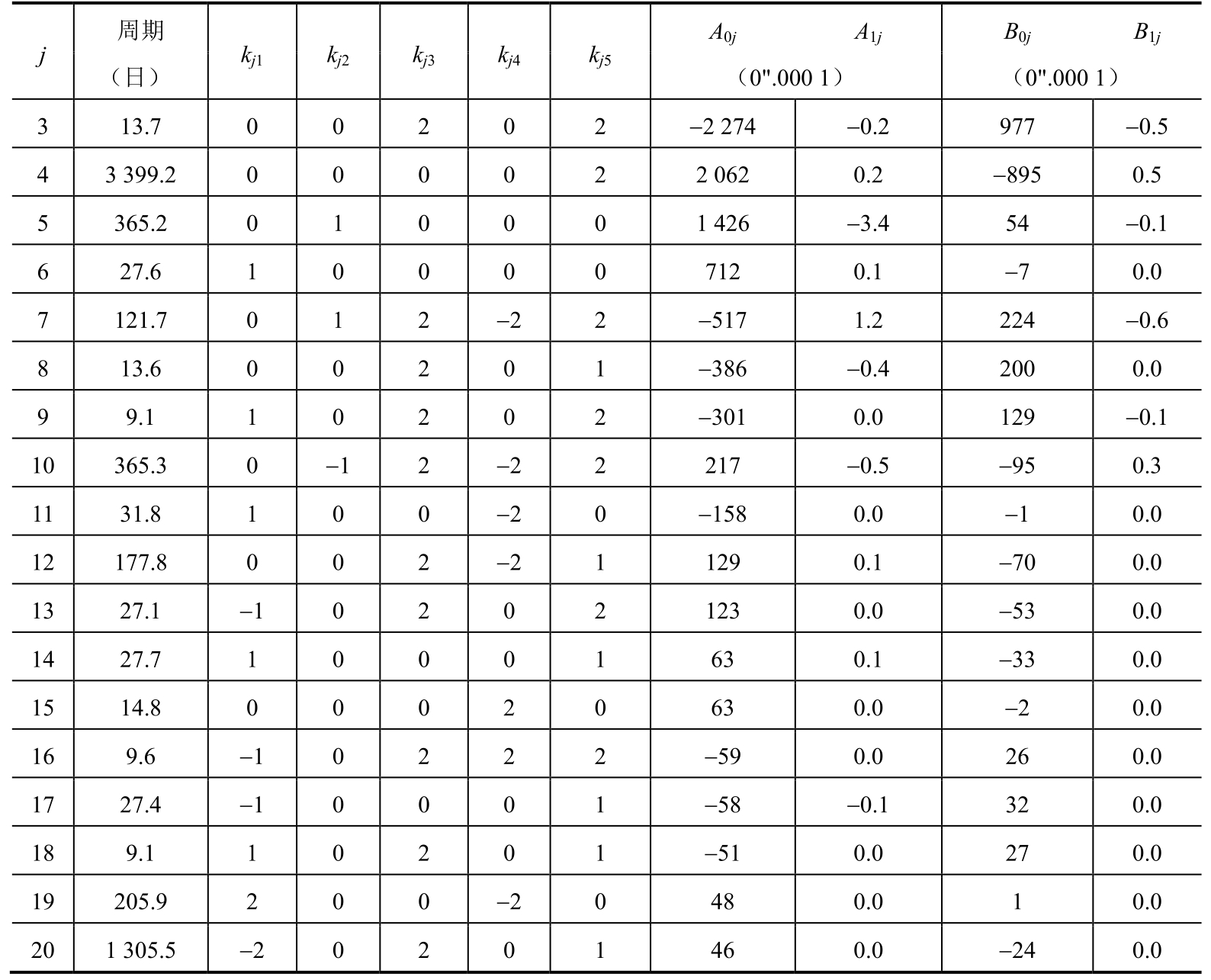
式(1.40)中涉及的与太阳和月球位置有关的5个基本幅角α i (i=1,…,5)的计算公式为

其中,1 r =360°,章动序列前 20 项的有关系数见表 1.3。如果按前面所说的米级精度考虑,公式(1.40)右端的A 1 j 和B 1 j 除表1.3中列出的A 11 和B 11 外亦可略去,但在具体工作中取项的多少,不仅需要符合精度要求,还应考虑相应软件的功能和适应性,如功能的扩张等因素。上述计算章动量的公式(1.40)~公式(1.43)中出现的t,即式(1.37)中所定义的世纪数T,但对应的是TDT时间。
表1.3 IAU(1980)章动序列的前20项

(续表)
上述内容中涉及的各旋转矩阵
R
x
(θ),
R
y
(θ),
R
z
(θ)的计算公式见式(1.22)~(1.24)。注意,旋转矩阵
R
x
(θ),…是正交矩阵,有
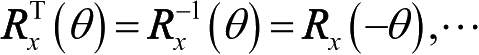 。
。
在 ⅠAU 2000 规范下,地心天球参考系(GCRS)到国际地球参考系(ITRS)的转换过程,可表示为
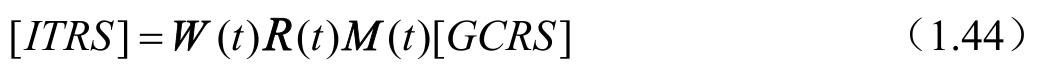
其中,[GCRS]和[ITRS]各对应前面
ⅠAU 1980
规范下的
地心天球坐标系
和
地固坐标系
。为了表达的连贯性,仍采用同一位置矢量在两个坐标系中的符号
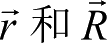 来表达变换关系,即
来表达变换关系,即

M (t)是岁差、章动矩阵, R (t)是地球自转矩阵, W (t)是极移矩阵。
关于岁差、章动矩阵 M (t),基于春分点的转换关系,岁差、章动矩阵可以写为

其中, N (t), P (t)和 B 分别为章动、岁差和参考架偏差矩阵。参考架偏差矩阵 B 已在前面有过说明,它是一个旋转量很小的常数矩阵,在直接引用 J2000.0平赤道坐标系 作为 地心天球坐标系 时,就作为单位阵略去,不再考虑,如有特殊需要,考虑它也极其简单,见式(1.46)。于是有

各矩阵的计算方法下面将分别给出。
在第24届国际天文联合会大会(2000年8月,Manchester)上通过决议,从2003年1月1日起正式采纳ⅠAU 2000岁差-章动模型取代ⅠAU 1976岁差模型和ⅠAU 1980章动理论。关于岁差章动的计算就是基于ⅠAU 2000模型,根据不同精度要求,又分为ⅠAU 2000A模型和ⅠAU 2000B模型,前者精度为0.2mas(毫角秒),后者的精度稍低,为1mas。下面对此作一简要介绍。
关于岁差量的计算,由标准历元J2000.0到计算历元,平赤道坐标系之间转换的三个赤道岁差参数ζ A ,z A ,θ A ,可由下式计算,即

其中,t是自标准历元J2000.0起算的计算历元(TT时刻)的儒略世纪数,即
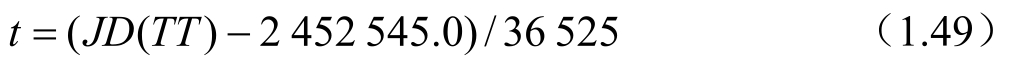
关于章动量的计算,ⅠAU 2000章动模型的黄经章动Δψ和交角章动Δε的计算公式为
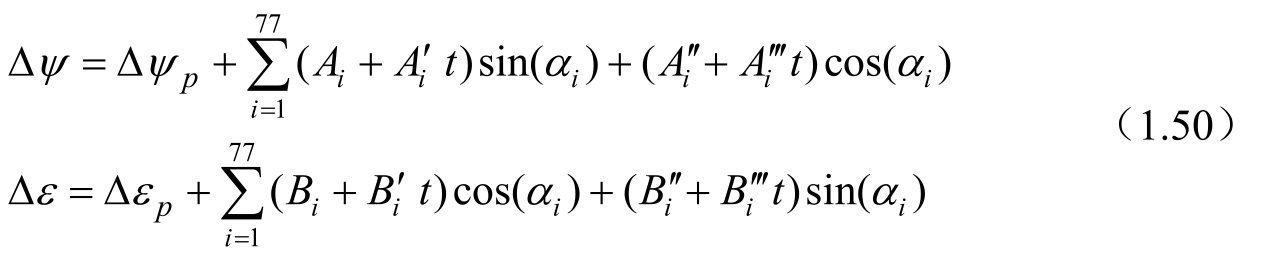
其中,Δψ p ,Δε p 是行星章动的长周期项,有

式(1.50)中t的意义同前,见式(1.49)。
章动序列中的幅角 i α同样可表示成5个基本幅角的线性组合形式,即
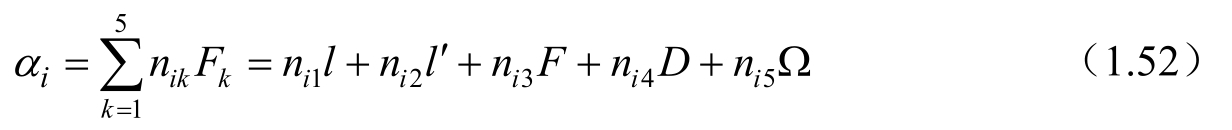
式中,n ik 是整数,5个与太阳、月亮位置有关的基本幅角F k 可表示为

这 5 个与太阳、月球位置有关的基本幅角F k (k=1,…,5),分别为月球的平近点角、太阳的平近点角、月球的平升交点角距、日月平角距和月球轨道升交点平黄经。F k (k=1,…,5)就是前面ⅠAU 1980 章动序列中出现的 5 个基本幅角α i (i=1,…,5),见式(1.43)。
为了比较对应ⅠAU 1980章动序列的前20项系数,同样列出ⅠAU 2000B章动模型前20项系数
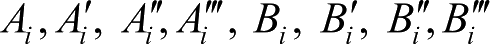 的主要部分,见表1.4。
的主要部分,见表1.4。
表1.4 IAU 2000B章动序列前20项的主要部分
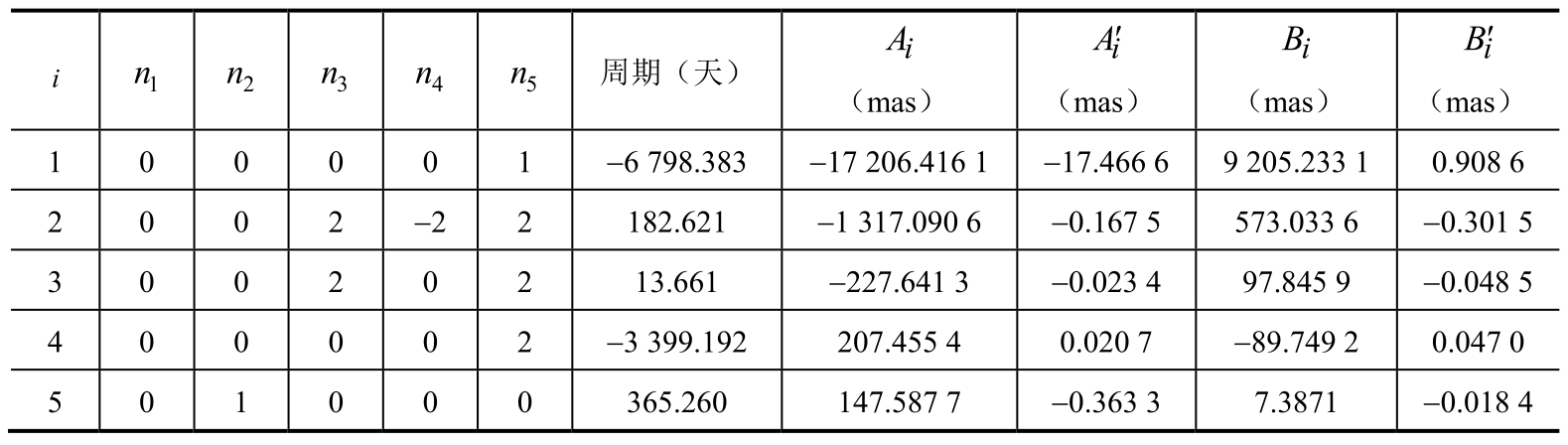
(续表)
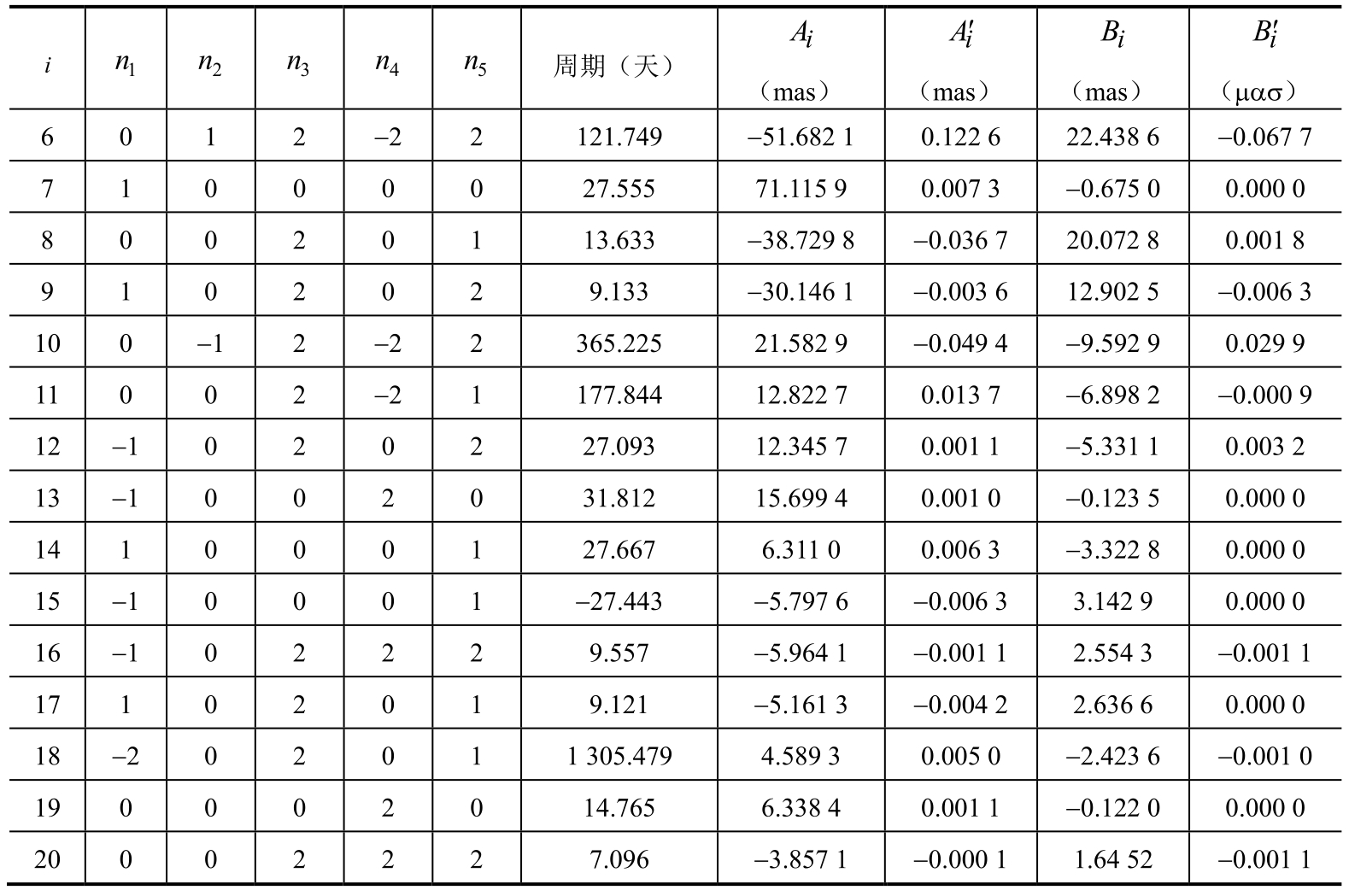
(1)传统的转换方式——三次旋转
计算公式为
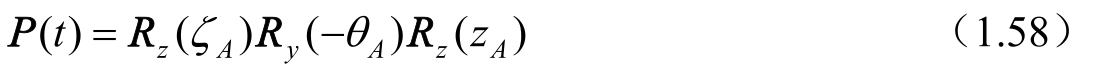
其中,各旋转角的计算公式见式(1.48)。关于这种传统的转换方式,赤道岁差角都是基本参数和球面三角关系得到的导出量,其中ζ A 和z A 在接近 J2000 的时刻,对参考架偏差矩阵 B 非常敏感,从而导致它们采用多项式表达时精度明显降低。为此,ⅠAU2000规范中又推荐了另一种四次旋转的岁差矩阵。
(2)新的转换方式——四次旋转
计算公式为
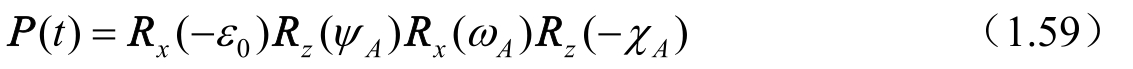
其中,后三个旋转角的计算公式为

ε 0 的计算见式(1.63)。式(1.60)中t的意义同式(1.49)。
关于上述两种转换方式,在实际工作中可视具体情况(包括相应计算软件的应用背景和精度需求)选择,一般情况下,差别完全可以忽略。
计算公式为
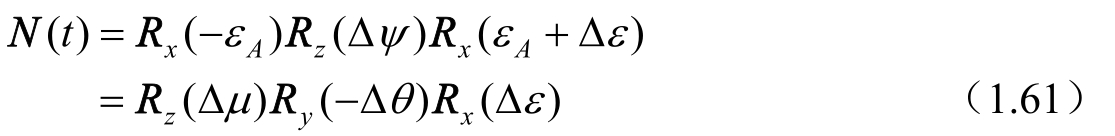
其中,Δμ=Δψcosε A ,Δθ=Δψsinε A ,分别是赤经和赤纬章动,Δψ是黄经章动,Δε是交角章动,ε A 为瞬时平赤道面与黄道面的交角,称为平黄赤交角,计算公式为
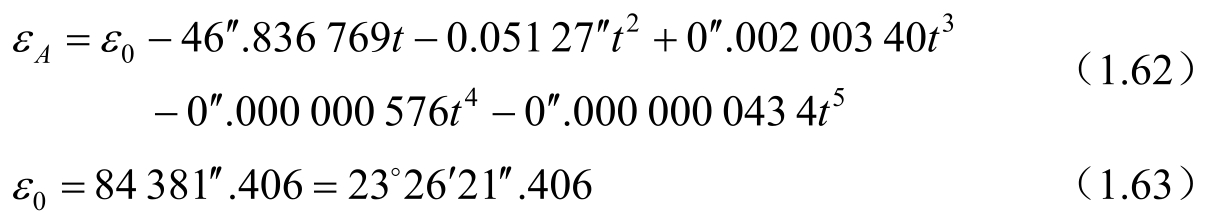
ε 0 为历元(J2000.0)平黄赤交角。
这与 ⅠAU 1980 规范有差别,涉及时刻t的格林尼治恒星时S G 的计算。 ⅠAU 2000 规范中格林尼治真恒星时GST 与地球自转角 ERA 有严格区别,见图1.3。图中所画圆周即表示地心参考系中的中间赤道,E 为地球质心,γ为春分点。
在天球参考系中观察时,中间赤道与 CⅠO固结,称为 天球中间赤道 ,TⅠO 沿赤道逆时针方向运动,周期为1 恒星日。在地球参考系中观察时,中间赤道与TⅠO 固结,称为 地球中间赤道 ,CⅠO 以同样周期沿赤道顺时针方向运动。这两种观察所反映的都是地球绕轴自转的运动,CⅠO 和 TⅠO 之间的夹角是地球自转角度的度量,称为 地球自转角ERA (Earth Rotating Angle)。在此前提下,矩阵 R (t)的计算公式变为
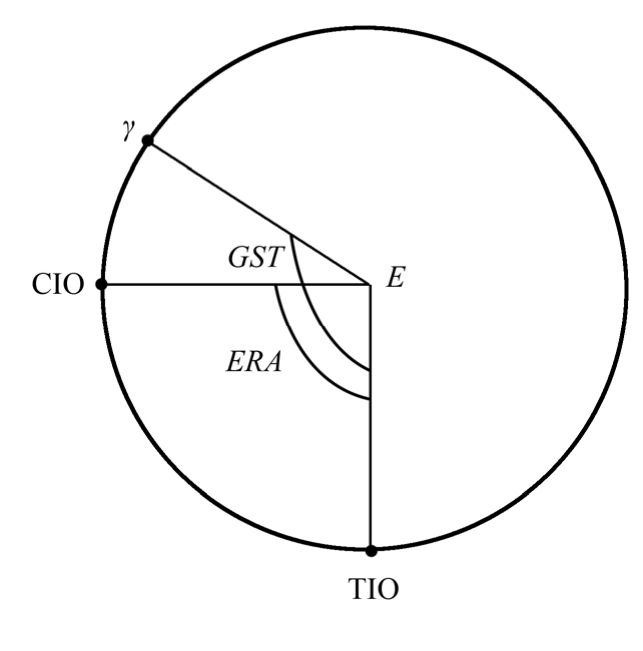
图1.3 中间赤道示意图

其中,GMST,EE分别称为格林尼治平恒星时和二分差(Equation of The Equinoxes),计算公式为

式(1.65)中的θ(UT1)为地球自转角 ERA ,是世界时UT1的线型函数,计算公式为
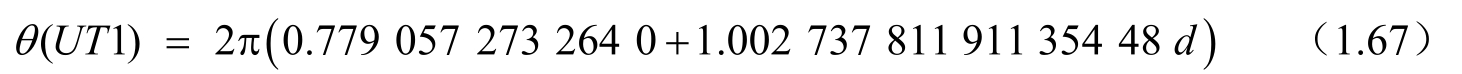
其中,d为自标准历元J2000.0起算的世界时儒略日数(对应UT1时刻),即

式(1.66)右端求和项的幅角和振幅列于表1.5中。
表1.5 α k ,C k 的值
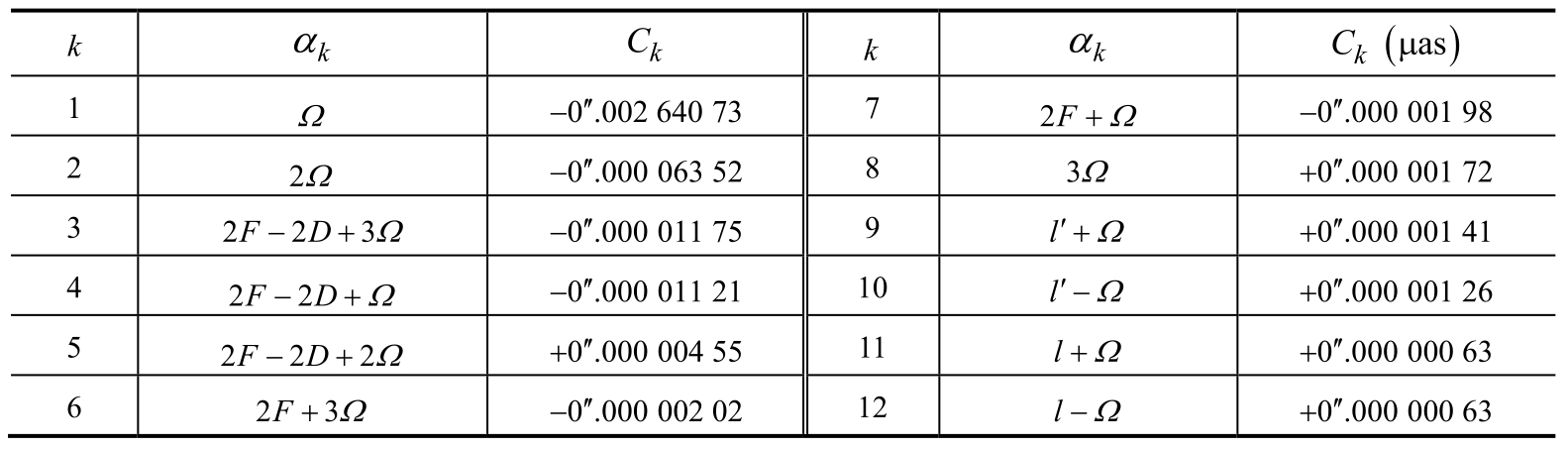
表1.5中的角 i α与式(1.50)中的 i α同类型,其涉及的基本幅角F k (F,D,Ω)可参见式(1.55)~式(1.57)。
与地球自转角不同,格林尼治真恒星时GST 是从真春分点起量的,它与ERA的关系为

其中,EO称为 零点差 ,与岁差、章动在中间赤道上的分量有关。根据ⅠAU 2006/2000A岁差-章动模型,零点差的表达式(包含在1975—2025 年之间,所有大于0.5μas的项)为
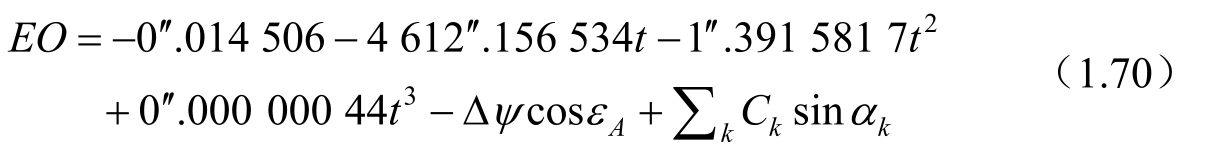
其中,t是从J2000.0 起算的儒略世纪数,参数α k 和振幅C k 见表1.5。
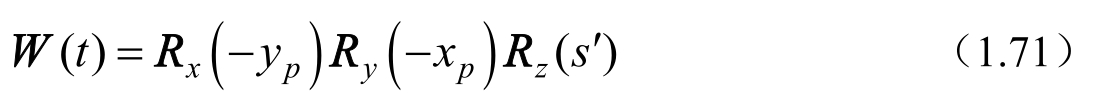
其中,x p ,y p 是天球中间极CⅠP在地球参考系(ⅠTRS)中的两个极移分量,s′称为地球中间零点TⅠO的定位角,提供TⅠO在CⅠP赤道上的位置,是x p ,y p 的函数,即
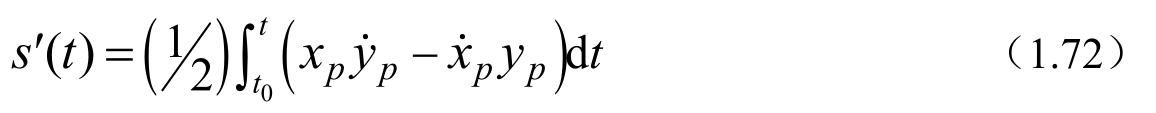
s′(t)无法事先获得,但其量级很小,可以用下列线性公式作为其近似

其中,t的定义同前,即计算时刻距标准历元J2000.0的儒略世纪数。
上述的ⅠAU 2000.0新规范与ⅠAU 1980规范,除岁差章动等有关参数有较小差别外,地球坐标系与天球坐标系的定义及相关符号的采用也与老规范的习惯用法有所差别,下面主要厘清两者的相关计算公式之间的对应关系。
在 ⅠAU 2000 规范中,天球参考系(Celestial Reference System,CRS)到地球参考系(Terrestrial Reference System,TRS)的转换关系为
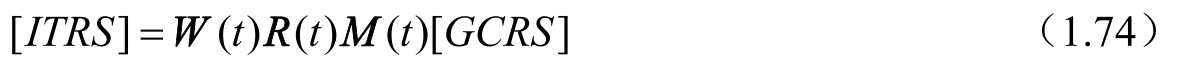
其中,
M
(t)是岁差、章动矩阵,
R
(t)是地球自转矩阵,
W
(t)是极移矩阵。而在
ⅠAU1980
规范下的习惯用法,即卫星在地球参考系和天球参考系的位置矢量分别为
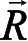 和
和
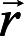 ,则式(1.74)转换关系可类似地写成下列形式,即
,则式(1.74)转换关系可类似地写成下列形式,即

应有如下的对应关系,即
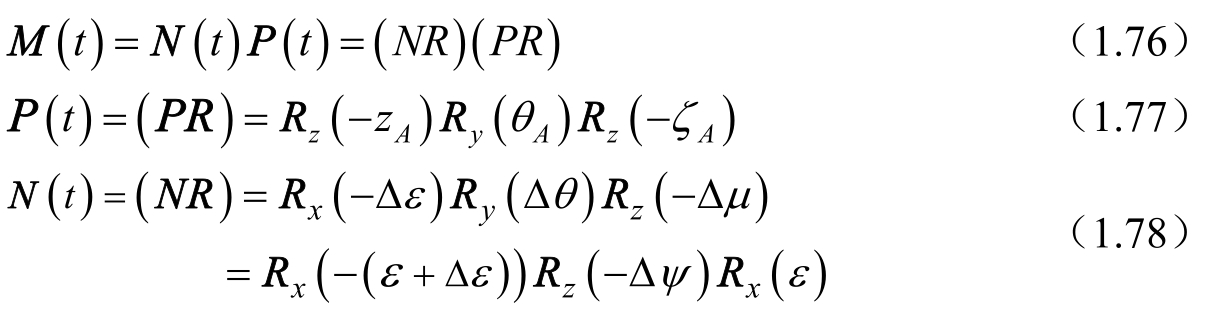
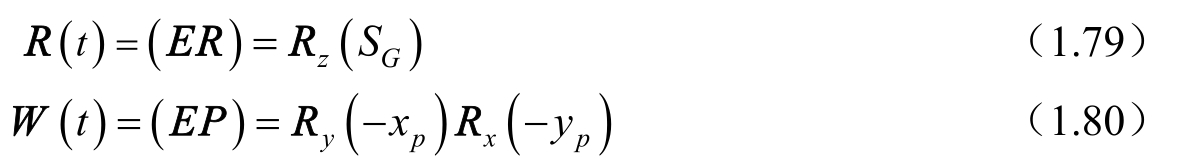
根据上述公式的比较不难看出,关于岁差(按三次旋转考虑)、章动和地球自转(两个规范中的格林尼治恒星时S G 稍有差异)三个相关矩阵,除相应的参数有微小差别外,转换过程和计算公式完全相同,只有极移矩阵的表达形式有差别,按 ⅠAU 2000 规范,极移矩阵 W (t)应由式(1.71)表示,即
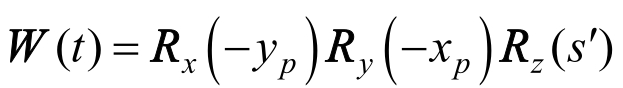
除增加一个微小的转动矩阵 R z (-s′)外,剩下两个转动矩阵 R y (x p ) R x (y p )却与式(1.80)的转动次序相反。但因为极移量x p ,y p 很小,转动次序的改变,引起的差别应该比极移量更小,最终的转换(指地球参考系与天球参考系的转换)结果不会有明显差别,作者已通过实际算例得到证实。
不仅地球自转矩阵如此,对于ⅠAU 2000与ⅠAU 1980两个规范,在地球参考系与天球参考系的位置矢量
 之间的完整转换中,亦无明显差别,在米级精度的前提下,新、老规范都可以用,而且对于章动序列只要取到前20项即可。在此处理下,两个规范计算的格林尼治恒星时与标准值(年历所载)之差都不超过0
s
.001,相应的位置量转换(包括
ⅠAU 2000
新规范中的两种岁差矩阵的转换方法)之差确实都在米级以内。
之间的完整转换中,亦无明显差别,在米级精度的前提下,新、老规范都可以用,而且对于章动序列只要取到前20项即可。在此处理下,两个规范计算的格林尼治恒星时与标准值(年历所载)之差都不超过0
s
.001,相应的位置量转换(包括
ⅠAU 2000
新规范中的两种岁差矩阵的转换方法)之差确实都在米级以内。