下载掌阅APP，畅读海量书库
立即打开
这里将定量分析系统误差对第3章中的迭代公式Taylor-a的性能影响，重点将推导迭代公式Taylor-a在系统误差存在条件下的估计方差矩阵。本节将所推导的估计方差矩阵与无系统误差条件下的克拉美罗界矩阵CRB （a） （u）进行比较，其目的在于定量评估系统误差对于定位精度所产生的影响。此外，本节还将所推导的估计方差矩阵与系统误差存在条件下的克拉美罗界矩阵CRB （b） （u）进行比较，从而可以明确是否需要进一步设计出能够有效抑制系统误差的Taylor级数迭代定位算法。
为了避免歧义，在系统误差存在条件下，这里将第3章中的迭代公式（3.11）中的第k次和第k 1+ 次迭代结果分别记为
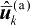和
（无系统误差时记为
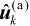和
），由于仅能够得到系统参量w的测量向量v，因此第3章的迭代公式（3.11）应该修改为
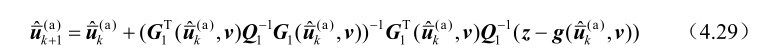
式（4.29）用测量向量v替换了第3章的式（3.11）中的真实向量w。若令式（4.29）的迭代收敛值为
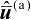（即
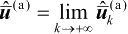），则对式（4.29）两边取极限可得
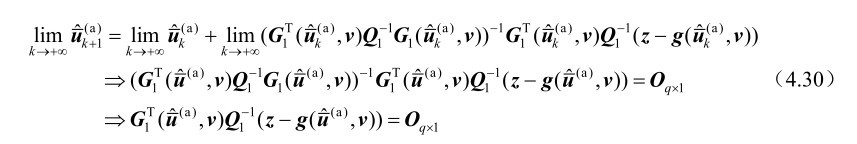
利用一阶误差分析方法可以推得
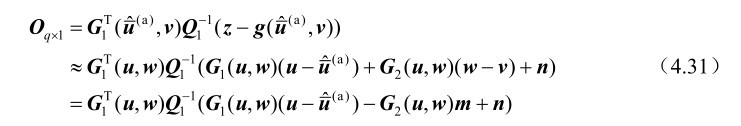
式（4.31）忽略了误差的二阶及其以上各项，由该式可以进一步推得定位解
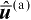的估计误差为
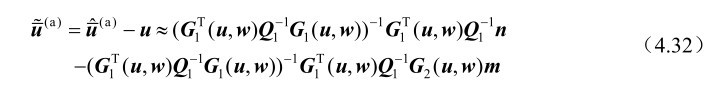
根据式（4.32）可知定位误差
服从零均值的高斯分布，并且定位解
在系统误差存在条件下的估计方差矩阵等于
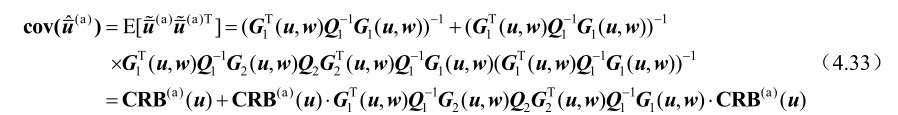
式（4.33）利用了观测误差n与测量误差m相互间统计独立的假设。
比较第3章的式（3.15）和式（4.33）可以首先得到如下命题。
命题4.2：
若G
1
（u,w）是列满秩矩阵，G
2
（u,w）是行满秩矩阵，则有
。
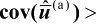
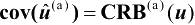证明： 首先分别定义如下3个矩阵：
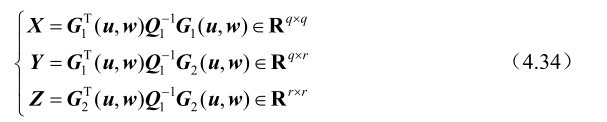
则根据第3章的式（3.15）和式（4.33）可得
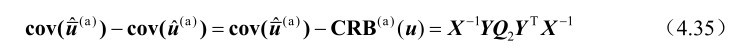
利用推论4.3中的分析可知X是满秩方阵，Y 是行满秩矩阵，再利用第2章的命题2.3和命题2.5可以证得
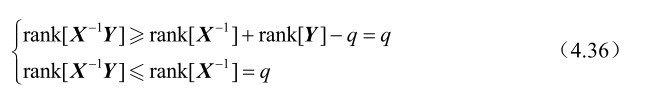
由式（4.36）可知
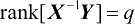，即X
-1
Y是行满秩矩阵，再利用第2章的命题2.13可知
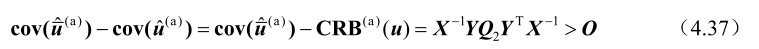
命题4.2得证。
命题4.2表明，系统误差会导致定位解Taylor-a的估计方差增加。
此外，比较式（4.17）和式（4.33）还可以进一步得到如下命题。
命题4.3：
若G
1
（u,w）是列满秩矩阵，则有
。
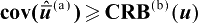证明： 首先分别定义如下3个矩阵：
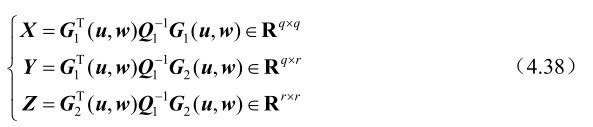
则根据式（4.17）和式（4.33）可得
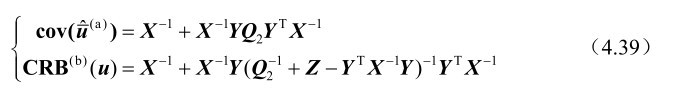
利用式（4.21）可知
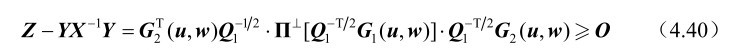
再根据第2章的命题2.15可得
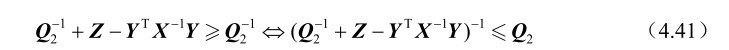
将式（4.41）代入式（4.39）中并利用第2章的推论2.7可知
。
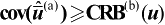命题4.3得证。
命题4.3表明，在系统误差存在条件下，定位解 Taylor-a的估计方差难以达到系统误差存在条件下的克拉美罗界（即CRB （b） （u）），因此它并不是渐近统计最优的估计方法，为此，下面将给出两类目标位置估计方差矩阵等于CRB （b） （u）的Taylor级数迭代定位算法。