4.1 定位观测模型及其参数估计方差的克拉美罗界

4.1.1 定位观测模型

考虑无源定位中的数学模型，其中待定位目标的真实位置向量为u（可包含目标位置和速度等参数），假设通过某些观测方式可以获得关于目标位置向量的空域、时域、频域或能量域观测量（如第1章所描述的各类定位观测量），则可以建立如下统一的（非线性）代数观测模型：

式中

z∈R ^p×1 表示实际中获得的定位观测向量；

u∈R ^q×1 （q≤p）表示待估计的目标位置向量（q≤p是为了保证问题的可解性）；

w∈R ^r×1 表示观测方程中的系统参量，在本书中主要是指观测站的位置和速度等参数；

z ₀ =g（u,w）表示没有误差条件下（即理想条件下）的观测向量，其中g（⋅,⋅）泛指连续可导的非线性观测函数，它同时是关于目标位置向量u和系统参量w的函数，由于这里并不限制特定的定位观测量，所以可用统一的函数形式来表征；

n∈R ^p×1 表示观测误差，这里假设它服从零均值的高斯分布，并且其方差矩阵等于Q ₁ =E[nn _T ]。

在很多情况下，系统参量w也是通过测量获得的，其中难免也会受到测量误差的影响，本书称其为系统误差，并特指因观测站位置和速度扰动所产生的误差，不妨假设其测量向量为v，则有

式中，m∈R ^r×1 表示系统参量的测量误差，这里假设它服从零均值的高斯分布，并且其方差矩阵等于Q ₂ =E[mm ^T ]，而且测量误差m与观测误差n相互间统计独立。

综合上述分析，在系统误差存在条件下，用于无源定位的观测模型可以联立表示为

下一小节将基于式（4.3）推导相应的参数估计方差的克拉美罗界。

4.1.2 参数估计方差的克拉美罗界

在系统参量w存在测量误差的条件下，未知参量将由u和w共同构成，此时需要推导两者联合估计方差的克拉美罗界，结果可见下述命题。

命题4.1： 基于式（4.3）中的观测模型，未知参量u和w联合估计方差的克拉美罗界矩阵可以表示为

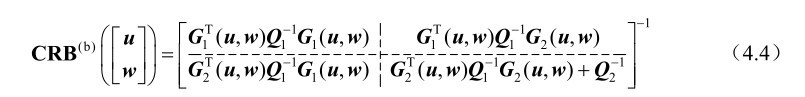
式中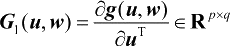， 表示函数g（u,w）关于向量u的Jacobi矩阵，它是列满秩矩阵，而 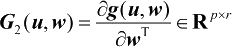表示函数g（u,w）关于向量w的Jacobi矩阵。

证明： 首先定义新的未知参量η=[u ^T w ^T ] ^T ∈R ^（q+r）×1 和新的观测向量 μ=[z ^T v ^T ] ^T ∈R ^（p+r）×1 。根据式（4.3）中的观测模型及其误差的统计假设可知，对于特定的参数η，观测向量μ的最大似然函数可以表示为

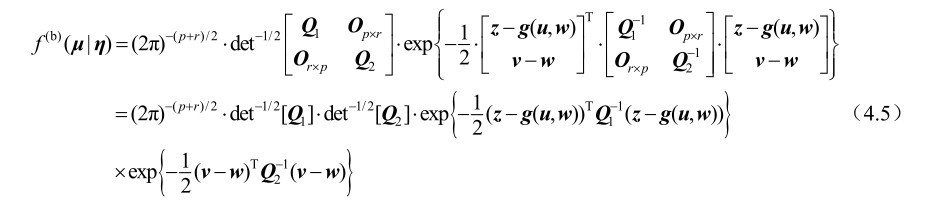
对式（4.5）两边取对数可得对数似然函数为

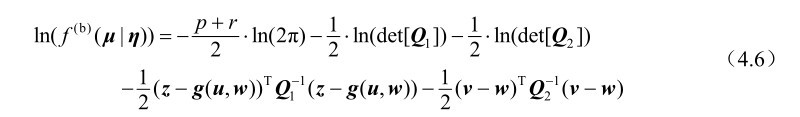
于是对数似然函数ln（f ^（b） （μ|η））关于向量η的梯度向量可以表示为

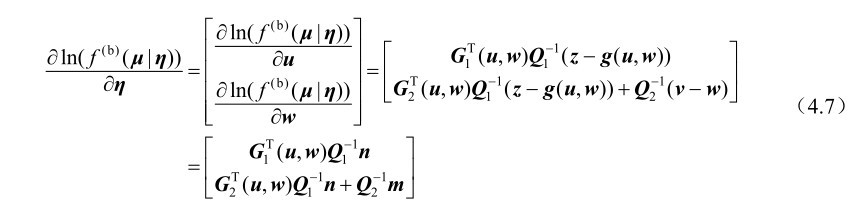
根据第2章的命题2.23可知，关于未知参量η的费希尔信息矩阵可以表示为

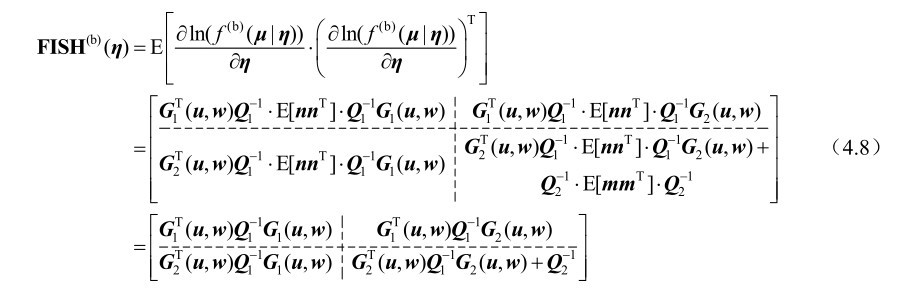
根据式（4.8）可知未知参量η的估计方差克拉美罗界矩阵等于

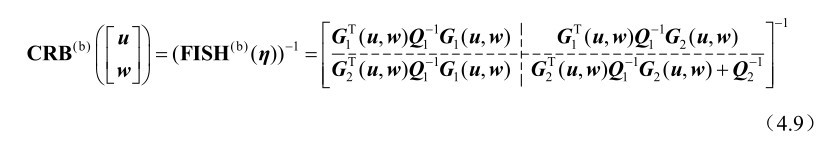
命题4.1得证。

根据命题4.1可以得到如下推论。

推论4.1： 基于式（4.3）中的观测模型，未知参量u和w联合估计方差的克拉美罗界矩阵可以分别表示为

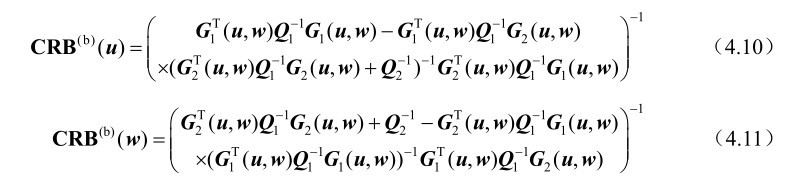
推论4.1可以直接由第2章的命题2.2证得。根据推论4.1还可以进一步得到如下3个推论。

推论4.2： 克拉美罗界矩阵CRB ^（b） （u）的另一种代数表达式为

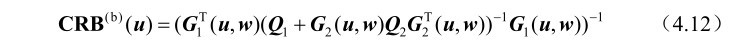
证明： 根据第2章的推论2.1可以得到如下等式：

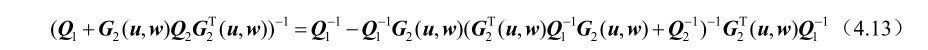
将式（4.13）代入式（4.10）中可得

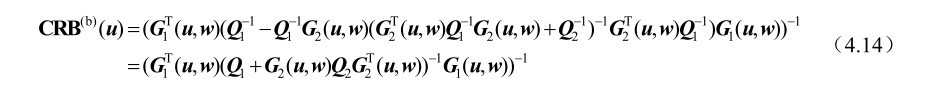
推论4.2得证。

推论4.2 表明，系统误差的影响可以等效为增加了观测向量z的观测误差，并且将观测误差的方差矩阵由原先的Q ₁ 增加至 。

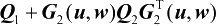推论4.3： 若G ₁ （u,w）是列满秩矩阵，G ₂ （u,w）是行满秩矩阵，则有CRB ^（a） （u）＜CRB ^（b） （u）。

证明： 首先分别定义如下3个矩阵：

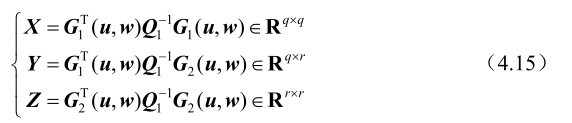
根据第3章的式（3.2）和式（4.10）可知

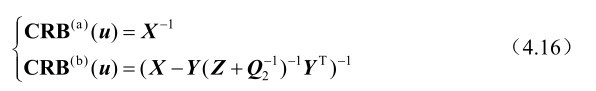
利用第2章的命题2.1可将矩阵CRB ^（b） （u）进一步表示为

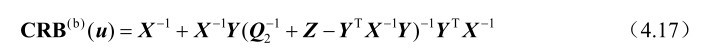
结合式（4.16）和式（4.17）可知仅需要证明

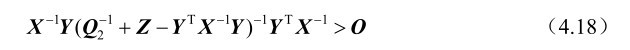
由于G ₁ （u,w）是列满秩矩阵，根据第2章的命题2.13可知X＞O，利用第2章的命题2.14可知式（4.18）等价于

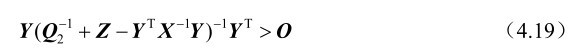
再次利用第2章的命题2.13 可知，为了证明式（4.19），需要证明Y 是行满秩矩阵及 。

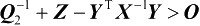由于G ₁ （u,w）是列满秩矩阵，G ₂ （u,w）是行满秩矩阵，结合第2章的命题2.3和命题2.5可知

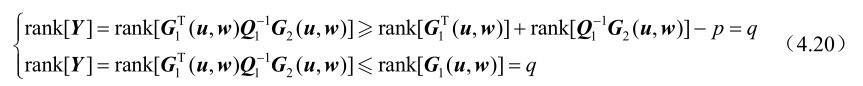
根据式（4.20）可知rank[Y]=q，即Y 是行满秩矩阵。另外，根据式（4.15），并结合第2章的命题2.20可得

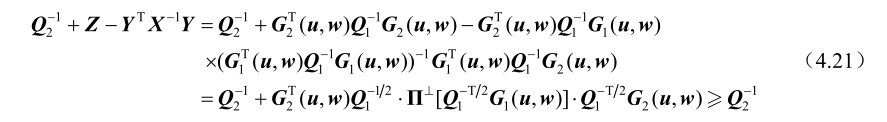
根据式（4.21）可知 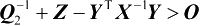，于是式（4.19）得证。

推论4.3得证。

推论4.3表明，系统误差的存在会增加目标位置估计方差的理论下界。

推论4.4： 若G ₁ （u,w）是列满秩矩阵，G ₂ （u,w）是行满秩矩阵，则有CRB ^（b） （w）≤Q ₂ ，进一步，当且仅当p=q时，CRB ^（b） （w）=Q ₂ 。

证明： 首先分别定义如下3个矩阵：

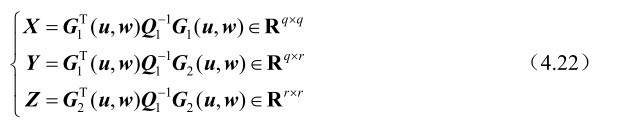
则根据式（4.11）可知

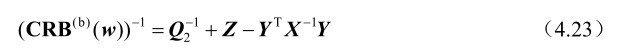
利用式（4.21）中的结论可知

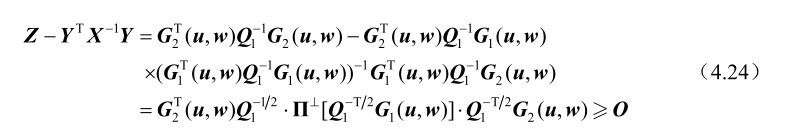
将式（4.24）代入式（4.23）中，并利用第2章的命题2.15可得

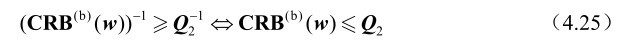
另外，当p=q时，G ₁ （u,w）∈R ^p×q 是可逆方阵，根据式（4.11）可得

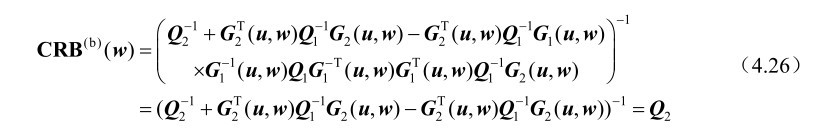
此外，若CRB ^（b） （w）=Q ₂ ，则结合式（4.23）和式（4.24）可知

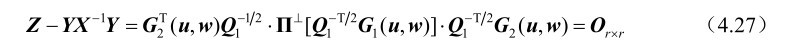
再利用矩阵G ₂ （u,w）的行满秩性及第2章的推论2.5可以证得

由于 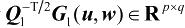是列满秩矩阵，根据第2章的推论2.12 可知 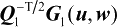必是满秩方阵，于是有p=q。

推论4.4得证。

推论4.4表明，若观测方程维数p等于目标位置向量维数q，则无法利用目标的观测量信息进一步降低系统参量估计方差的理论下界，只有当观测方程维数p大于目标位置向量维数q时，才可能利用目标的观测量信息进一步降低系统参量估计方差的理论下界。 /vPfJTy9VPS61MmwMD/lB4wDM5LaCW8zykEDlod2rTJbh+Kam61edzJsJ+CM0YXV