





在无系统误差条件下(即系统参量w精确已知),无源定位问题就是根据观测向量z估计目标位置向量u,当p=q时(即观测方程数等于未知参量个数),直接求解该非线性方程组即可,此时并不需要考虑观测误差n的统计特性,因为在这种情况下并没有“残差分配”问题;但是当p>q时(即观测方程数大于未知参量个数),就不能直接求解该非线性方程组了,因为误差向量n的存在会导致观测方程没有精确解,此时就需要考虑观测误差n的方差矩阵,以对误差进行最优的加权分配,从而取得渐近最优的统计性能。下面将在系统参量w精确已知的条件下建立相应的定位优化模型,并给出求解该优化模型的Taylor级数迭代定位算法。
根据第2章的命题2.24可知,最大似然估计器具有渐近最优的统计性能,即其参数估计方差可以渐近逼近相应的克拉美罗界。再利用第2章的命题2.25可知,在高斯误差假设条件下,最大似然估计器可以等价为求解如下非线性加权最小二乘优化模型:
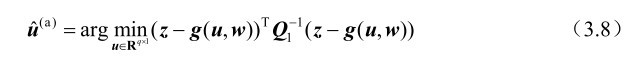
式中,
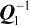 的作用是为了抑制观测误差n的影响。由于g(⋅,⋅)通常是非线性函数,因此求解式(3.8)不可避免地需要数值迭代。这里将给出基于 Taylor级数展开的迭代算法,其在数值优化理论中又称为Gauss-Newton 迭代法。该迭代算法的基本思想是利用最新的迭代值对非线性函数g(⋅,⋅)作线性近似,从而在每次迭代求解过程中能够将式(3.8)近似转化成一个二次优化问题,基于此就可以获得下一次迭代值的更新公式,然后再重复此过程直至迭代收敛为止。
的作用是为了抑制观测误差n的影响。由于g(⋅,⋅)通常是非线性函数,因此求解式(3.8)不可避免地需要数值迭代。这里将给出基于 Taylor级数展开的迭代算法,其在数值优化理论中又称为Gauss-Newton 迭代法。该迭代算法的基本思想是利用最新的迭代值对非线性函数g(⋅,⋅)作线性近似,从而在每次迭代求解过程中能够将式(3.8)近似转化成一个二次优化问题,基于此就可以获得下一次迭代值的更新公式,然后再重复此过程直至迭代收敛为止。
假设第k次Taylor级数迭代得到目标位置向量的结果为
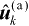 ,现利用一阶Taylor级数展开可得
,现利用一阶Taylor级数展开可得
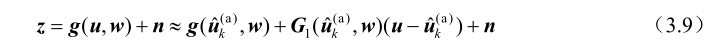
将式(3.9)代入式(3.8)中,就可以得到求解第k+1次迭代结果的线性加权最小二乘优化模型为
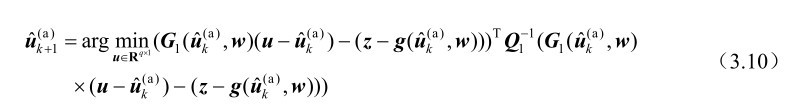
显然,式(3.10)是关于目标位置向量u的二次优化问题,因此其存在最优闭式解,根据第2章的式(2.152)可知该闭式解为
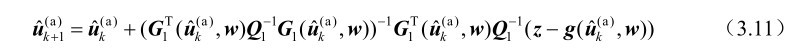
式(3.11)即为无系统误差条件下的Taylor级数迭代定位算法,并称其为迭代公式Taylor-a。这里将其收敛值记为
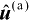 (即
(即
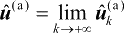 ),并称其为定位解Taylor-a。
),并称其为定位解Taylor-a。
下面将定量推导定位解
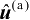 的理论估计性能,并证明其在无系统误差条件下的估计方差矩阵等于克拉美罗界矩阵CRB
(a)
(u)。首先对式(3.11)两边取极限可得
的理论估计性能,并证明其在无系统误差条件下的估计方差矩阵等于克拉美罗界矩阵CRB
(a)
(u)。首先对式(3.11)两边取极限可得
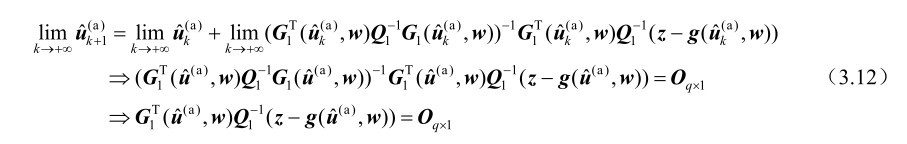
利用一阶误差分析方法可以推得
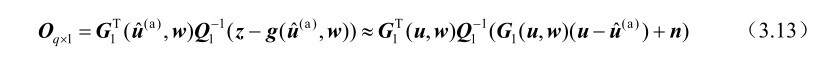
式(3.13)忽略了误差的二阶及其以上各项,由该式可以进一步推得定位解
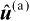 的估计误差为
的估计误差为
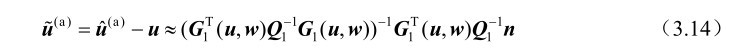
根据式(3.14)可知定位误差
 服从零均值的高斯分布,并且定位解
服从零均值的高斯分布,并且定位解
 的估计方差矩阵等于
的估计方差矩阵等于
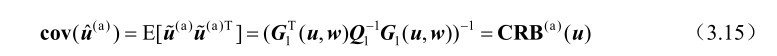
式(3.15)表明,定位解
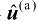 在无系统误差条件下具有渐近最优的统计性能,即其具有最小的估计方差。
在无系统误差条件下具有渐近最优的统计性能,即其具有最小的估计方差。