




所谓可靠性是指产品在规定的条件下,规定的时间内,完成规定的功能的概率。“规定的条件”是指使用时的环境条件和工作条件;“规定的时间”是指产品完成规定的任务所经历的时间。对广播卫星来说,通常是指卫星定点后在轨道上开始广播一直到丧失所规定的广播功能所经历的时间。“规定的功能”中的功能是指产品的技术指标。例如广播卫星的发射信道数量和等效全向辐射功率等指标。
可靠性也叫可靠度,或叫生存概率。它是时间t的函数,可用R(t)表示可靠性函数。假若有可用的大量产品,并能精确地控制环境条件,则可用统计实验方法来获得R(t)。此R(t)称为可靠性函数或可靠度函数。
上面讲了可靠性,同它对立的则是不可靠性。不可靠性通常用故障率或失效率来表示。所谓产品出故障或失效是指该产品丧失所指定的功能。
假设待试的产品总数为N S ,经试验时间t后仍然合格的产品数为N R ,出故障的产品数为N F ,则可靠性函数R(t)可表示为
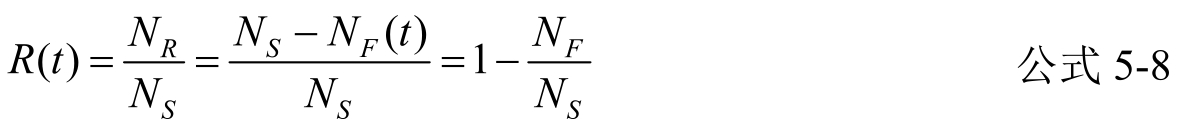
由上式可知,产品出故障的数目N F (t)随时间的增长而增加,一直到等于N S 为止。与此对应,R(t)随时间增长而减小,当N F =N S 时,它变为零。
对上式微分,可得可靠性随时间的变化率

因一个事件,只有可靠和不可靠两种可能。若设不可靠性为F(t),则一个事件出现可靠和不可靠的概率之和应是

将F(t)对时间t微分一次称为故障发生的时间比率,即为故障密度函数,其值为

由此可见,故障密度函数即为可靠性函数的负导数。
将公式5-9代入公式5-11得

即故障密度函数是单位时间内失效产品数比上参试的总产品数。
在可靠性分析中,另一个重要参数是产品的失效率或称故障率。它被定义为单位时间内失效产品数比上还在工作的产品数。
若设故障率为λ,则由定义得

将公式5-12和公式5-8代入上式得

将上式两边积分可得

上式是常用的可靠性函数公式。它由故障率唯一决定。
将上式代入公式5-11可得
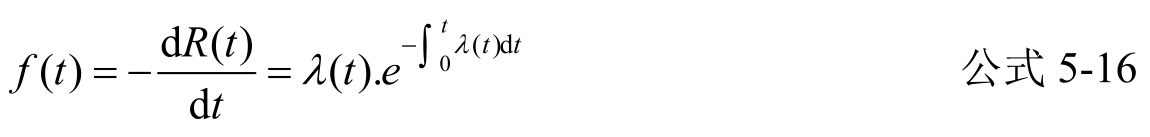
上式是故障密度函数公式。它也由故障率唯一决定。
经试验证明,相当大的一部分元器件和产品它们的可靠度R(t)、故障率λ(t)和故障密度函数f(t)随时间t的变化关系如图5-18所示。
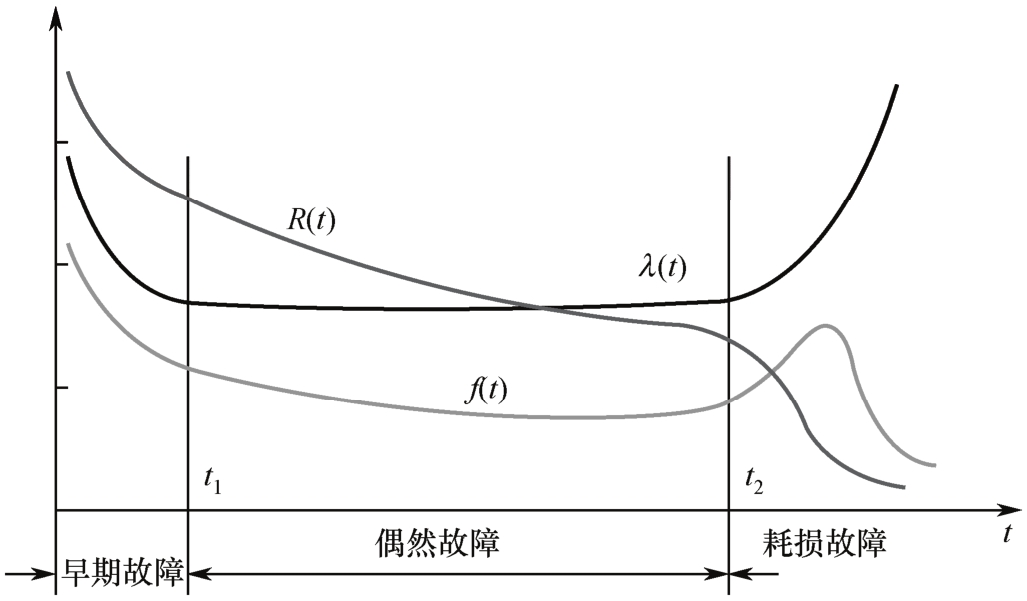
图5-18 产品典型的可靠度、故障率和故障密度函数曲线
图中,时间t 1 和t 2 把曲线分成三段。第一段和第三段失效率λ(t)高、第二段失效率λ(t)低,整个失效率λ(t)随时间t的变化形如浴盆,也称浴盆曲线。
第一段称早期失效期,失效率高,但随着时间的推移迅速下降。产品失效原因主要由材料及工艺上的缺陷造成。
第二段称偶然失效期,故障率甚小且接近于常数。它是由多种偶然的,都不占绝对优势的因素综合作用的结果。一般产品使用都在此时期,此时期也称有效使用寿命期。
第三段为耗损失效期,或称老化故障过程。它是由于产品老化使故障迅速增加的时期。它主要由产品老化、磨损、损耗和疲劳等原因引起。
对上述三段(或三个时期)我们最关心的是有效使用寿命期(第二段)。对可靠性问题讨论均指这个时期。
平均寿命:是指产品在失效前的平均工作时间。
设同时发射多颗同类的人造卫星,一直观察到全部卫星失效为止。然后求全部卫星的寿命平均值此值即为平均寿命。
令从卫星运行开始时起到Δt时卫星的生存数为N R ,因为这些卫星具有Δt的寿命,故它们的总寿命为N R ×Δt,但N R 随时间而减小,一直到t无穷大总寿命为L S ,则有

现设原来发射的卫星总数为N S ,则每颗卫星的平均寿命

又因为卫星的生存概率

将公式5-17和公式5-19代入公式5-18得

上式即为卫星的平均寿命。由此可见,只要知道卫星随时间变化的可靠性函数,即可求得它的平均寿命。
当R(t)为指数分布时,上式为
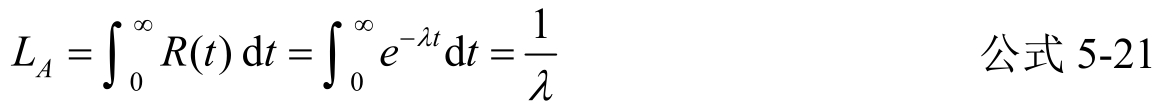
式中λ为故障率(常数)。
前已提到,可靠性函数R(t)是随时间单调下降的函数。其极限值为

因此,对 R(t)可以给定一个值γ(0≤γ≤1),就可算出 R(t)降到γ的工作时间,使可靠性R(t)等于给定值γ的时间t称为可靠性寿命,记为L R ,前面所述的γ称为可靠性水平。根据上述定义,有

当可靠性R(t)的分布为指数分布时,即

则有

经变换得

由上式可知,在可靠性函数 R(t)为指数分布时,只要知道了失效率λ,定了可靠性水平γ,就可求得可靠性寿命L R 。
所谓有效性,概略地讲就是产品完成某项任务的有效程度。或是指产品在特定时间内正常工作的概率。有效性也称可用性、可用度、可用率或运转率。它较多地应用于可维修产品。
对可维修产品(例如地球站),有效性用下述公式表示:
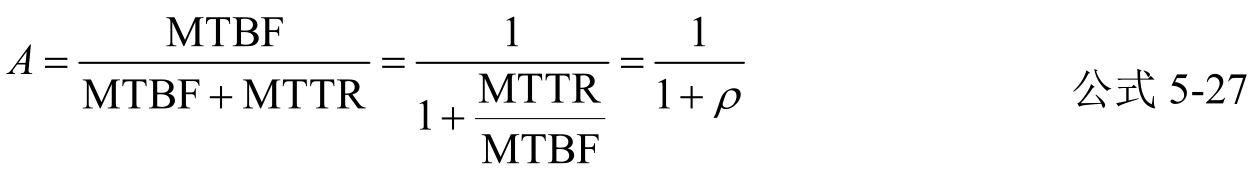
式中,MTBF为平均无故障工作时间;MTTR为平均修理时间;ρ为MTTR与MTBF之比,叫做维修比。
由公式5-27知,对可维修产品,只要知道维修比,即可求得有效性。
对不可维修产品(例如通常的人造卫星)可用如下公式求可用度。
设某系统在t 0 时刻进入工作状态,则到t时刻维持其功能的概率,即可用度

上式的表达形式是很清楚的。分子
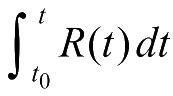 是系统从t
0
到t时刻内平均无故障工作时间,它相当于公式5-27的MTBF。分母t-t
0
是总时间,它相当于公式5-27的MTBE+MTTR。由公式5-28还可看出,A(t)由R(t)唯一决定,且随时间单调下降。我们容易理解,A(t)与R(t)一样,都是表示产品可靠性的物理量。R(t)表示产品不出故障的程度;A(t)表示产品随时可用的程度。
是系统从t
0
到t时刻内平均无故障工作时间,它相当于公式5-27的MTBF。分母t-t
0
是总时间,它相当于公式5-27的MTBE+MTTR。由公式5-28还可看出,A(t)由R(t)唯一决定,且随时间单调下降。我们容易理解,A(t)与R(t)一样,都是表示产品可靠性的物理量。R(t)表示产品不出故障的程度;A(t)表示产品随时可用的程度。
当R(t)为指数分布时,公式5-28可变为
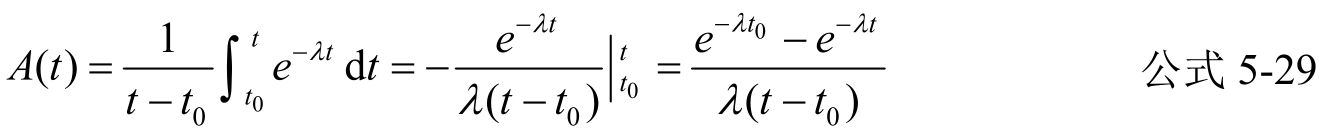
以上对可靠性的一些基本参数进行了介绍,这些参数有:可靠性函数,故障密度函数,故障率、平均寿命、可靠性寿命和有效性。从这些参数的表示式可以看到它们相互间关系。其中最主要的参数是故障率λ(t),只要知道了产品的故障率λ随时间t的变化规律,就可由公式5-15计算可靠性函数R(t),由公式5-16计算故障密度函数f(t)。在求得了可靠性函数R(t)后,可利用公式5-20求产品的平均寿命L A ,或利用公式5-26求可靠性寿命L R 。最后,在已知R(t)的情况下,利用公式5-28还可计算不可维修产品的可用度A(t)。
一个系统通常由若干分系统或许多部件组成。由于系统与分系统之间可以有不同的关系,各分系统之间也可能有不同的联系和影响。这些特征均会影响系统的可靠性。
若一个系统由n个部件A 1 、A 2 、…A n 组成,当任一个A i 失效,会引起整个系统失效,则此系统为串联型可靠性系统。如图5-19所示。

图5-19 串联型可靠性系统方框图
再设上述系统各部件中任一个部件失效不会导致其余部件从属失效,即各部件产生失效相互独立,则整个系统的可靠性R(t)等于各部件的可靠性R i (t)的乘积,即有

假设各部件的可靠性相等,即R 1 (t)=R 2 (t)=…=R n (t)=Rc(t)
则有

从上式可以看到:当用多个高可靠部件和—个不可靠部件串联工作时,—个不可靠部件会导致整个组合的可靠度大大下降。此外,用许多部件串联成复杂系统,其部件越多,系统可靠性越低。
例如国际通信卫星-3卫星的设计寿命为5年,对应各分系统的可靠性估算如表5-8所示。
表5-8 国际通信卫星-3卫星的可靠性估算
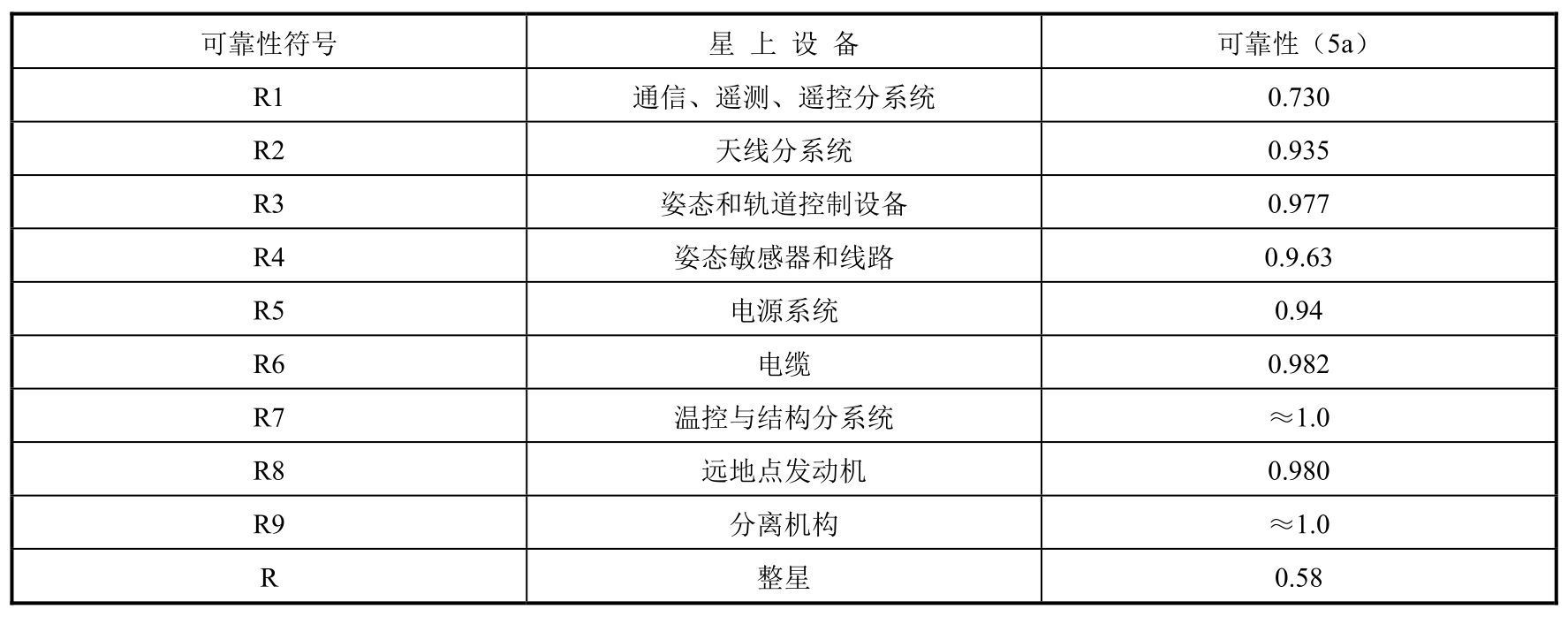
现假设各分系统相互独立,且任一个分系统失效就会导致整星功能失效。因此,其故障模式属串联型可靠性系统。应用公式5-31可计算得整星在设计寿命为五年末期可靠性如下:
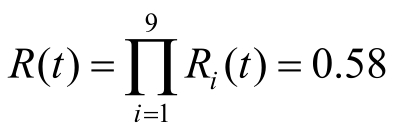
对并联型系统,所包含的部件中,只要有一个处于正常工作状态,整个系统就处于正常工作状态。其方框图如图5-20所示。
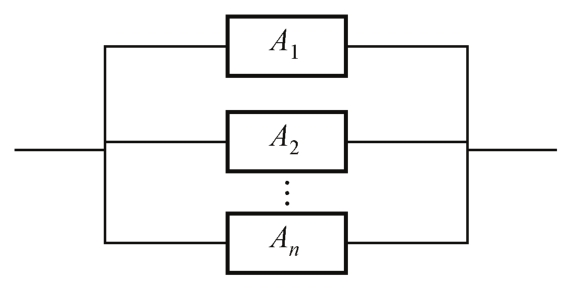
图5-20 并联型可靠性系统方框图
因为对并联系统,只有所有部件失效才整个系统失效,所以其系统可靠性为
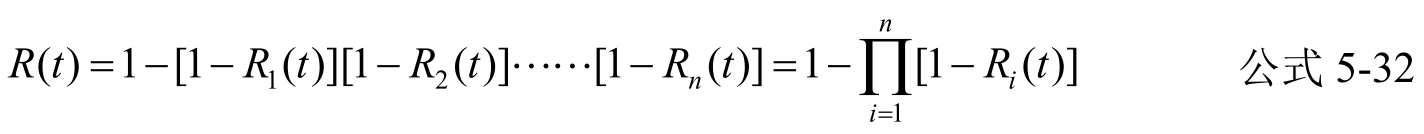
当各部件的可靠性相等时,即R 1 (t)=R 2 (t)=…=R n (t)=R c (t),则有

从上两式可以看出,并联系统可靠性显著高于串联系统可靠性。同时还告诉我们,可以采用并联冗余备份的办法来增加系统可靠性。所增加的部件,并非工作必需,而是为了提高系统可靠性。
例如,某种地空导弹每发击中敌机的概率R c 为0.85,求连发三发,击中敌机的概率。因为三发导弹击中敌机的概率是相互独立的,任意一发击中敌机就算完成击中敌机的任务,所以三发导弹构成一个并联系统可靠性模式,其击中概率
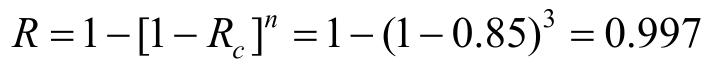
设一系统有n个相互独立具有相同可靠性函数R i (t)的部件组成。设此系统n个部件中至少有k个部件工作正常,系统才算工作正常;即当失效的部件数≤n-k时,系统工作正常,当失效的部件数>n-k 时,系统失效,此系统我们称它为 k-n(G)系统。现求此系统至少有 k个部件工作正常的可靠性函数R(t)。
我们知道由n个部件中取出j个的组合数为
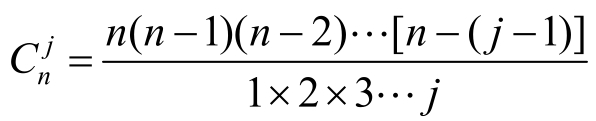
n个中任意j个部件工作正常的概率为
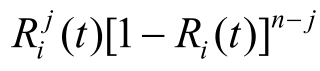
n个中所有组合j个部件工作正常的概率为
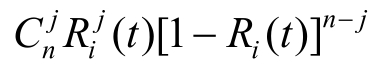
最后得n个部件中至少有k个工作正常的概率
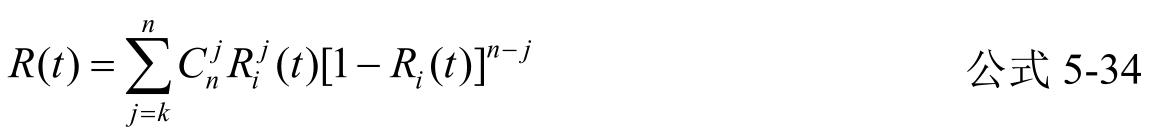
设每个部件可靠性服从指数律分布,其失效率为λ,即
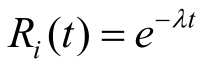
则公式(5-34)变为
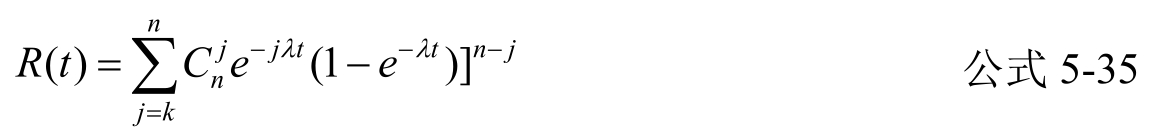
现举例说明之。设一颗通信卫星具有16部转发器,各转发器可靠性均服从指数分布律,且故障率λ均为0.015052/年,求工作t年后至少有k个转发器工作的概率R(t)。
因已知n=16,λ=0.015052/年,故只要确定t和k值后即可利用公式5-35计算得R(t)。计算结果见表5-9和图5-21。
由表5-9和图5-21可以清楚地看到,对一定的k值,R(t)随着t的增长而逐渐下降,同样,对一定的t值,R(t)随着k值的增长也逐渐下降。
表5-9 t年后n个转发器至少有k个转发器工作概率
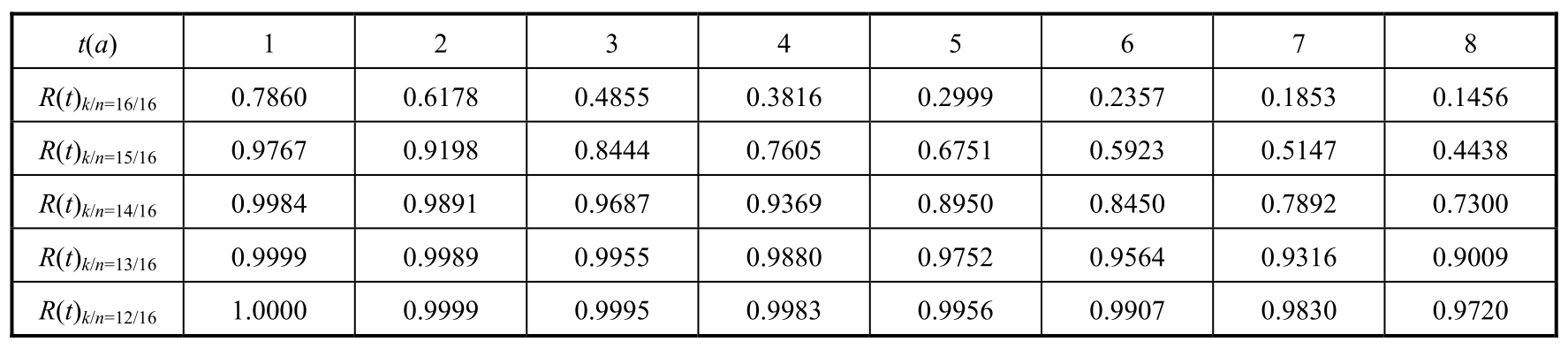
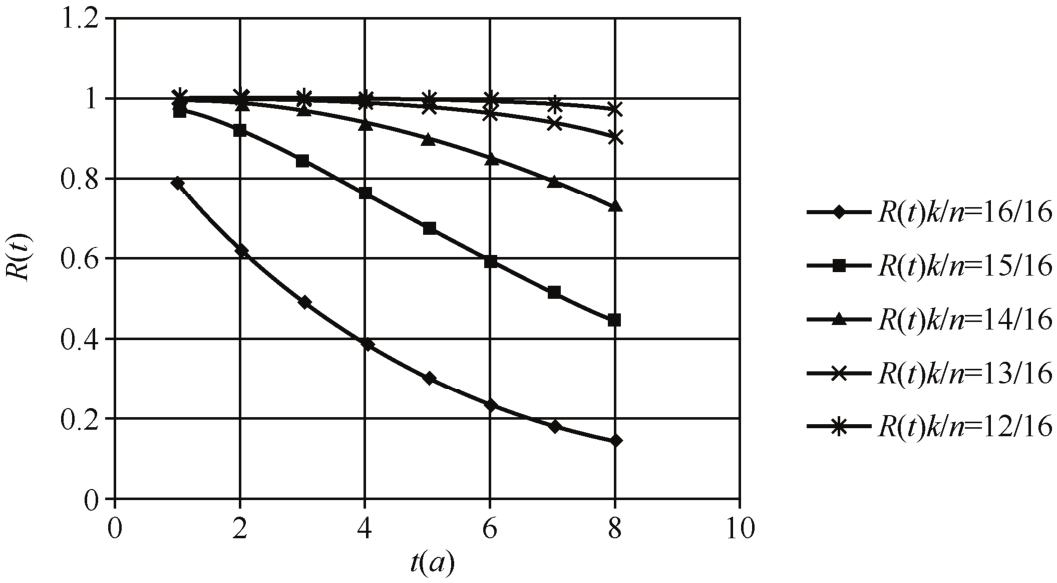
图5-21 t年后n个转发器至少有k个转发器工作概率
在通信系统中,系统的可靠性常用线路可用度来表示。线路可用度是指与系统用户相连接的线路,在规定的时间内,按规定的容量和质量满意地工作的概率。
对卫星通信系统来说,从终端用户的观点来看系统线路的可用度,要求下面几部分设备和电波传播处于正常工作:
地球站发射系统;上线电波传播;卫星;下线电波传播;地球站接收系统。
如果上述各项的可用度分别为A 1 、A 2 、A 3 、A 4 和A 5 。则整个线路的可用度为

卫星和地面站的可用度可以做得很高,但它要求选用优质部件和备有充分的备份件。上下行线路电波传播的可用度对10千兆赫以上频率,主要受天气影响,为了克服这种影响需使用大天线和大功率放大器,以增大上行线路和下行线路的等效全向辐射功率。
在美国的商业卫星系统(SBS)中,终端至终端的线路可用度指标和各部分可用度指标如表5-10所示。
表5-10 美国的商业卫星系统(SBS)可用度分配示例

上面对上线电波传播和下线电波传播的可用度要求均为0.998,即要求信号传输过程中由于坏天气而使线路中断时间不超过可通信时间的0.2%。
中国卫星广播系统线路可用度分配示例见表5-11所示。
表5-11 中国卫星广播系统线路可用度分配示例

描述通信卫星的可靠性特性通常使用两种方法:在通信卫星设计中,常用可靠性(或称生存概率)来表示;在卫星通信线路设计中,常用可用度来表示。
在静止轨道通信卫星设计中,用可靠性表示法是给出卫星进入静止轨道定点位置后从开始工作到寿命结束整个寿命时间段内n个转发器中k个能正常工作的随时间变化的概率。在对外的技术文件中,一般只给出特征值:一个是初期工作的可靠性。另—个是寿命末期的可靠性。例如国际通信卫星和美国的国内通信卫星COMSTAR等卫星都用这种方法表示的,其数值如表5-12所示。
表5-12 静止轨道通信卫星可靠性表示法示例
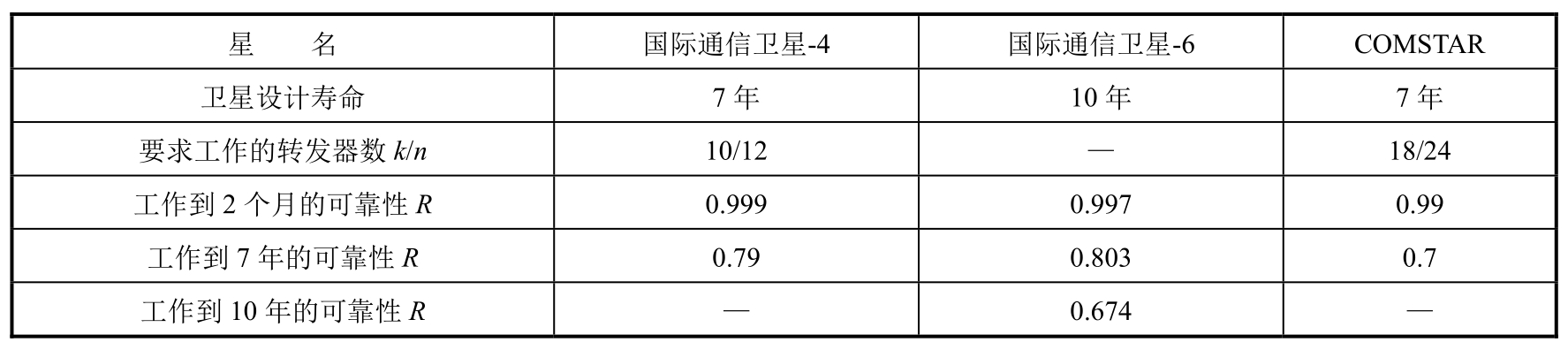
在卫星通信线路设计中,当以可用度表示卫星可靠性特性时,也是以卫星入轨开始工作作为时间起算点。
在研究卫星可用度时,必须注意卫星可用度与地球站可用度模式差别。我们知道,到目前为止,卫星在天上出故障后尚不能送人到轨道上进行修理,一般都称它是不可维修产品。但是只要在卫星上采取一定措施,人们可以在地面通过无线电遥测遥控跟踪站对卫星进行维修。
为使卫星成为—个可维修的产品(尽管维修能力很有限),最主要的措施是采用备份设计。因为这种措施方法简单、效果明显。若卫星设计中考虑了足够的备份部件或备份设备,则可以使它在某些部件或设备出故障时通过更换备份后仍能继续使用。例如,用户遇到在用转发器末级功率放大器出故障,则可通过地面遥控设备使它转换到备用放大器上工作。
卫星上绝大多数部件都有可能发生故障,而有些部件是难以备份的。因此,为做到万无一失,有必要采取整星备份。目前,对一些工作型卫星(非试验型卫星),在天上提供使用时,为了做到一旦工作卫星出故障能及时用备份卫星接替,备份卫星采用在轨备份方式。例如,“国防通信卫星-2”共发射四颗,三颗分别定点于太平洋、印度洋和大西洋上空。第四颗卫星进入轨道后就作为三颗卫星的备份星。又如太平洋上空有两颗“国际通信卫星-4”型卫星,代号为F4和F8,其中一颗投入使用,另一颗作备份。
一般的备份方式采用切换备份方式。即当地面站监视系统发现并查明卫星某个工作部件出故障时,立刻向卫星发遥控指令,将它切换到备用部件上去,使卫星很快排除故障重新正常工作。应该说,这也是一种修理方式。只是这修理方式是在地面上用无线电遥测遥控跟踪方法对卫星实行远距离自动切换。不像对地面站维修,人可以直接接触设备进行维修。
因此,有备份切换能力的卫星,可以把它看作可维修产品,使用可维修系统的可用度计算公式。即前面已给出的公式5-27。
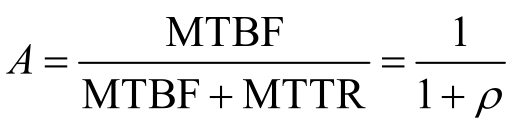
为了给出整星的可用度A,必须估算在卫星使用寿命期间可能出现的一些故障及排除它所需的时间。例如若有一卫星的MTBF=7年,MTTR=6小时,则用上式可计算得其可用度可高达0.9999。此数据相当于前述的美国早期的SBB卫星的设计数据。
卫星的可用度至少部分地是听天由命的,而地面站则不然。从原则上讲,地面网络中任何设备或元部件出故障,都可用一定方法进行现场修理。这是因为在地面对地面设备直接检查和修理比在地面通过测控站对卫星进行监测和修理(目前只能切换备份)条件要好得多。其中一个十分优越的条件是地面设备受质量、尺寸和耗电约束比卫星小得多,因此,对地面站各种设备和零件,原则上都可采用备份设计。
通常地面站是在不断维修中运转的,它的寿命可以比卫星长得多。影响地球站可用度的因素为:有无备份系统;现用和备份系统转换形式;故障部位监测的难易程度;排除故障的难易程度等等。
考虑了备份设计等一些措施,国际通信卫星用的大型标准地站,可用度的设计指标一般要求大于99.9%上。
当一个系统有n个部件串联时,若已知各部件可用度分别为A 1 、A 2 、…A n ,则系统的可用度A可表示如下:

式中ρ i 分别为各部件的维修比。
当一个系统有n个部件并联时,若已知各部件可用度分别为A 1 、A 2 、…A n ,则系统的可用度A可表示如下:
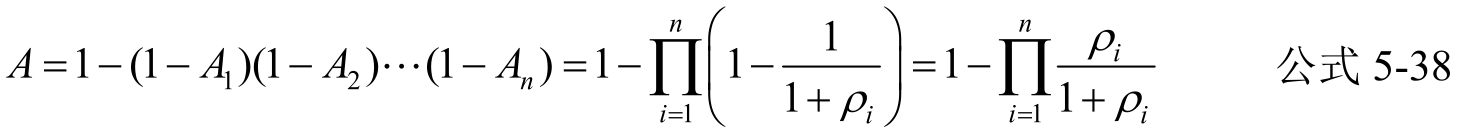
将上述两公式与公式5-30和公式5-32比较,其形式相同。因此,我们可视需要,采用可靠性函数或可用度来衡量一个系统的可靠性。
实际计算可用度A时,为便于运算,往往用维修比ρ来分配各件的指标,因为在可用度A接近1(或维修比ρ远小于1时)时,与ρ有下述近似式:
串联式:
当ρ 1 、ρ 2 …ρ n 均远小于1时,
公式5-37可近似得
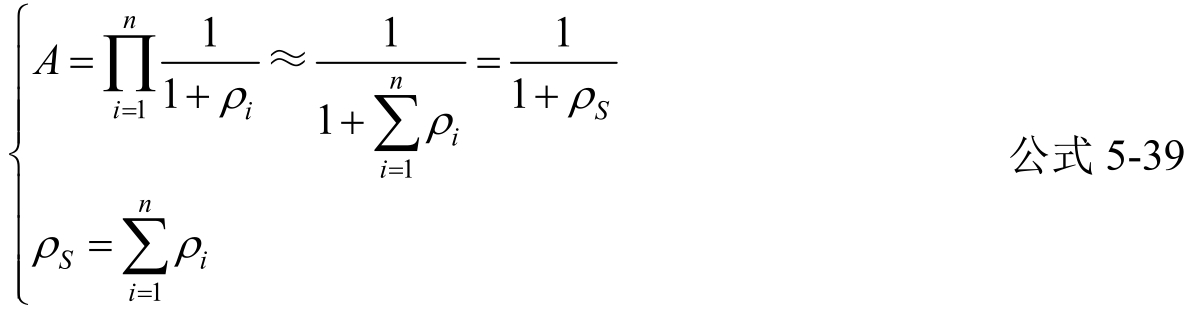
并联式:
当ρ 1 、ρ 2 …ρ n 均远小于1时,
公式5-38可近似得
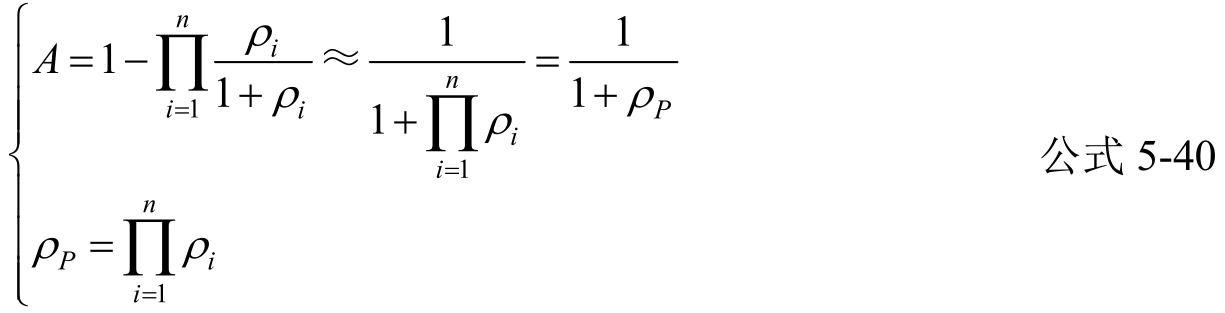
由上述串联型和并联型可用度A与维修比ρ的关系式知,当A≈1,或ρ□ 1时,可以近似认为:串联型系统的维修比为各部件维修比之和;并联型系统的维修比为各部件维修比之积。利用此特性,可以很方便地对实际系统进行可用度估算。
图5-22和图5-23依次是一典型的大型地球通信站天线设备和无线收发设备可用度分配(实际用维修比ρ来分配)示意图。
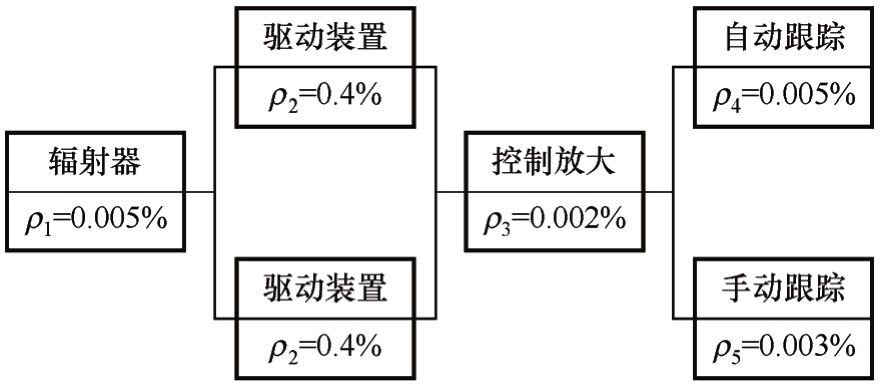
图5-22 天线设备维修比分配图
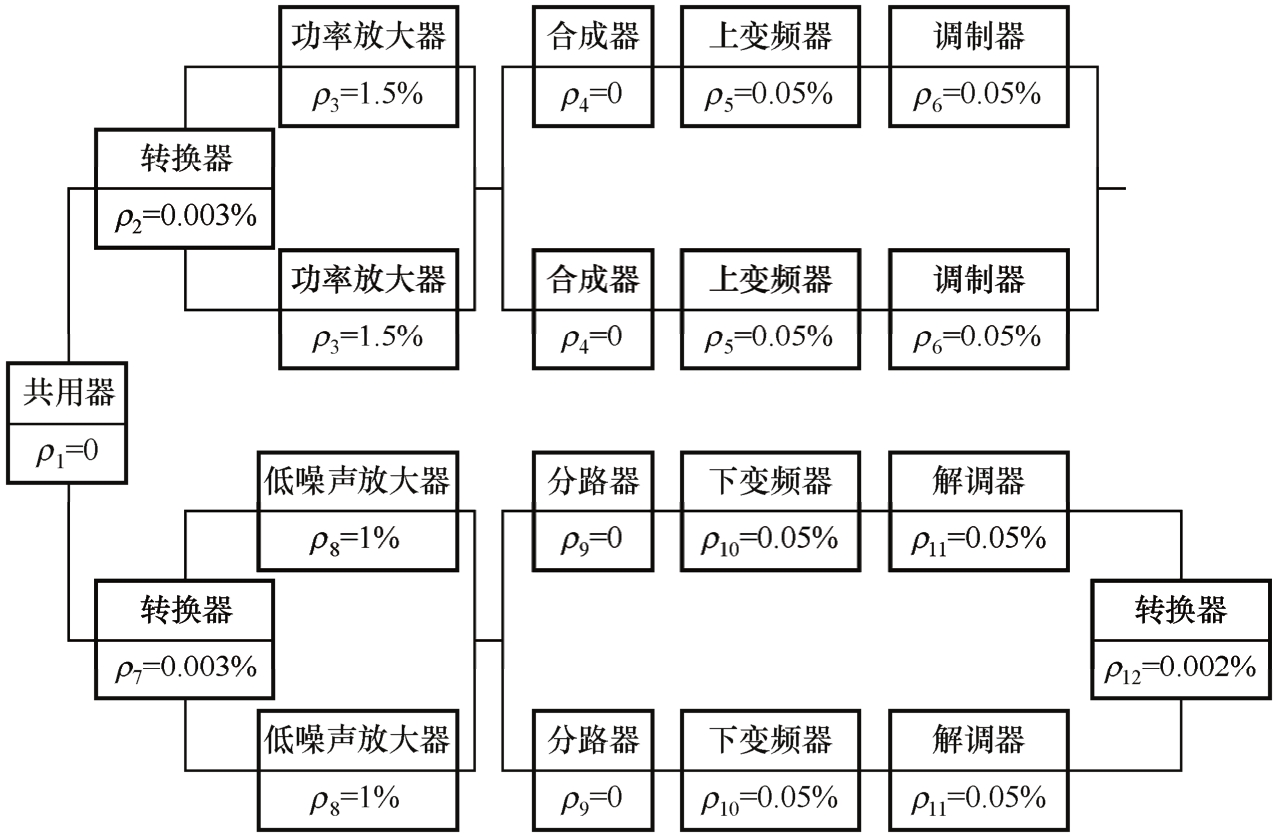
图5-23 无线收发设备维修比分配图
由图5-22得天线设备维修比
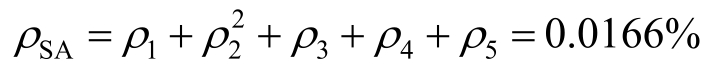
由图5-23得无线设备维修比
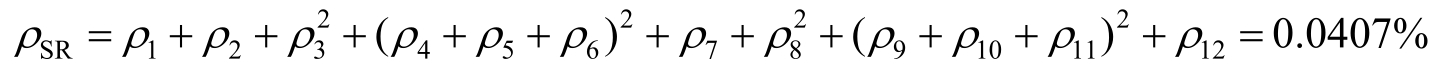
将天线设备和无线设备合在一起得整个地球站维修比
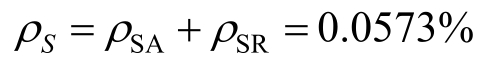
由公式5-27得整个地球站可用度
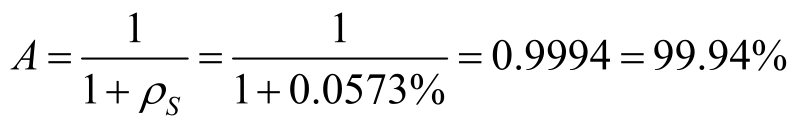
由上述结果知,其可用度大于99.9%。
上下行线路电波传播的可用度主要是针对降雨和大风等气候条件而言的。降雨使电波衰减和接收系统噪声增加。强风使天线摆动,从而使接收电平衰落,降低信噪比。
对K频段卫星通信来说,影响传播可用度的主要因素是降雨引起的损耗和噪声温度增加,且其影响随着地区不同而有差别。其影响分析参见本书第8章有关降雨损耗相关内容。