





海水的声速是指声波在海水中传播的速度,是决定海洋声传播特性的最基本的物理参数之一。声速与海水的压缩性有很大关系,可表示为
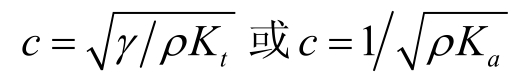
式中 c——海水声速(m/s);
γ——定压比热容和定容比热容之比;
ρ——海水密度;
K t ——等温压缩系数;
K a ——绝热压缩系数(压缩系数定义为海水体积的相对变化与相应的压力变化的比值)。
由于ρ和K a 与温度、盐度及静压力(或深度)有关,因此,声速可表示为温度、盐度及静压力(或深度)的函数。例如:Medwin(1975)提出的6项声速经验公式,即
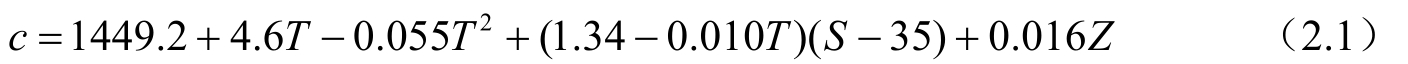
式中 c——海水声速(m/s);
T——海水温度(℃);
S——海水含盐度(‰);
Z——海水深度(m)。
通常,海水中的平均声速近似为1500m/s。声速随温度、盐度和压力的增加而增加。在这3个因素中,温度对声速的变化影响最大。温度每增加1℃,声速的增量约为4m/s;盐度每增加1‰,声速的增量约为1.1m/s;而压力每增加1atm(相当于水深增加10m),声速增量仅为0.175m/s。
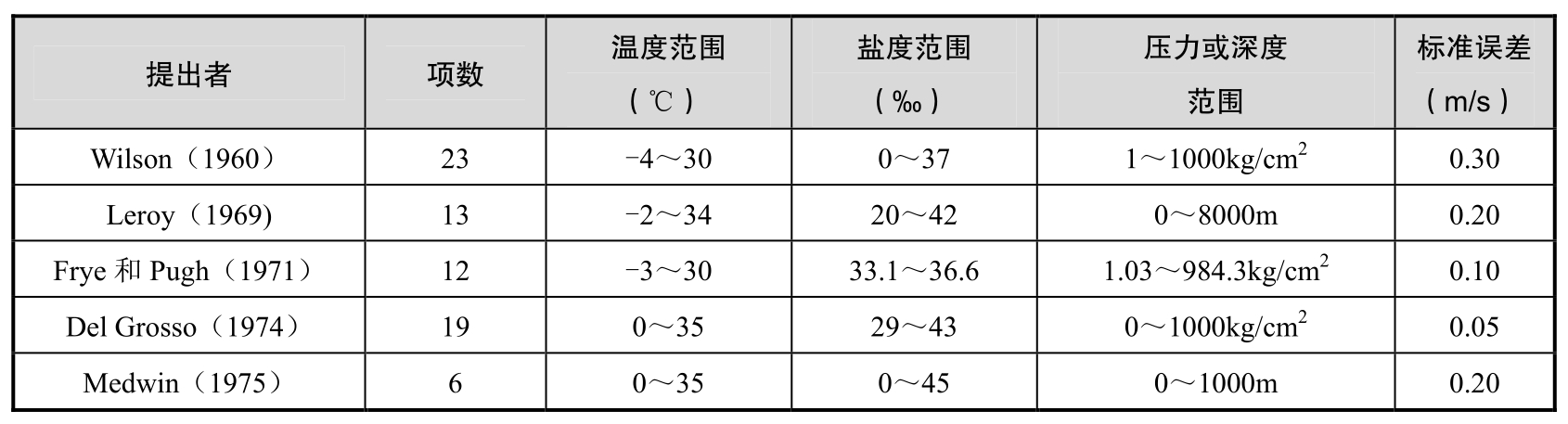
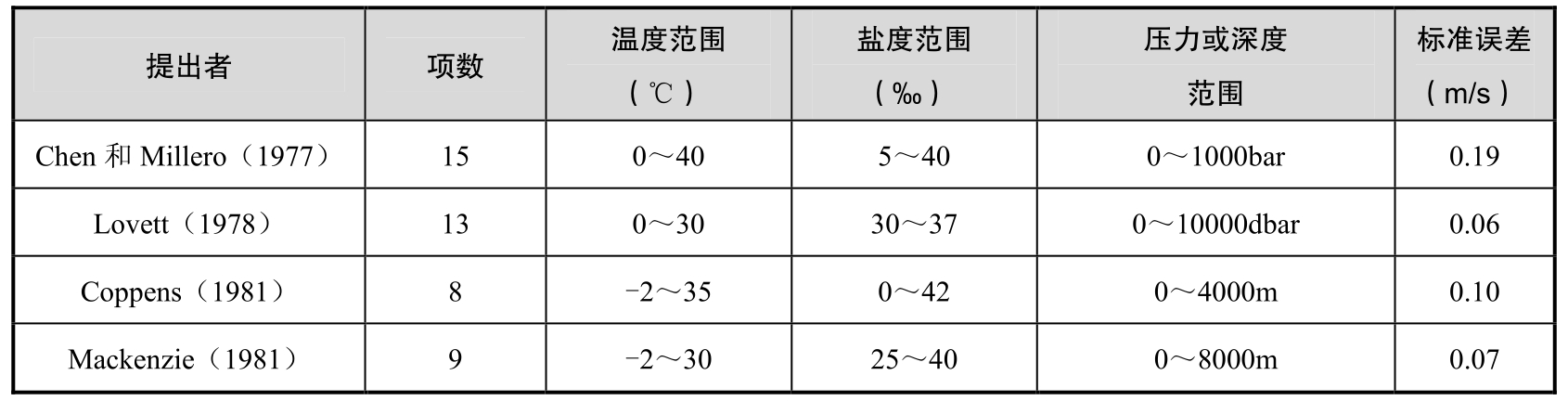
关于声速计算的经验公式目前已建立了几十种,其中比较常用的表达式参见表2.1。这些公式所含的参数项从几项到几十项不等,但都有关于海水温度、盐度和压力的适用范围,在超出这些范围的条件下使用时很可能导致错误的结果。在这些公式中,对于垂直空间的变量,有的使用压力,有的使用深度,两者的关系为:水深每增加10m,压力增加约10dbar(1bar)或1kg/cm 2 。压力与深度的转换算法可参考Leroy(1969)或Mackenzie(1981)。
表2.1 声速经验公式总结(Etter,2003)
续表
对海水声速起主要作用的是海水温度,因此声速分布一般与海水温度分布具有相近的区域性特征,其等温线或等声速线一般呈东-西向分布,如图2.2所示。这种分布主要是不区分地理纬度的太阳辐射差异造成的。在一些局部区域,由于洋流、上升流等作用,其等温线也会出现偏离东-西向的分布,在大陆沿岸或近海区域也时常有等温线的变化。
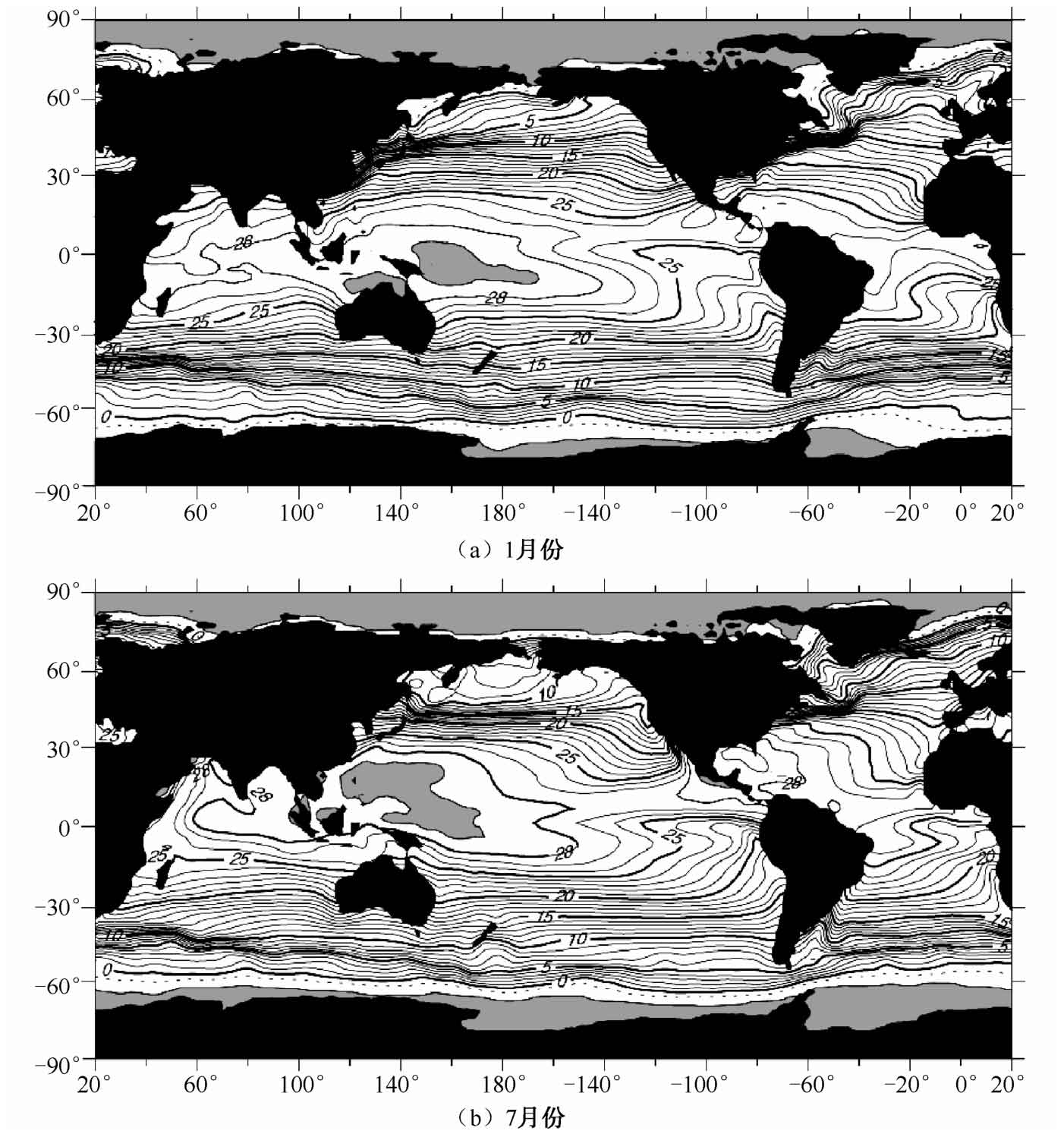
图2.2 1月和7月全球海面平均水温分布(Reynold和Smith,1995)
通常,海水温度和盐度在水平方向的变化要比垂直方向小得多,因此海水声速可近似认为主要是在深度方向上的变化。这种情况下海水可视为分层介质,等温线和等声速线近乎平行分布,如图2.3所示。
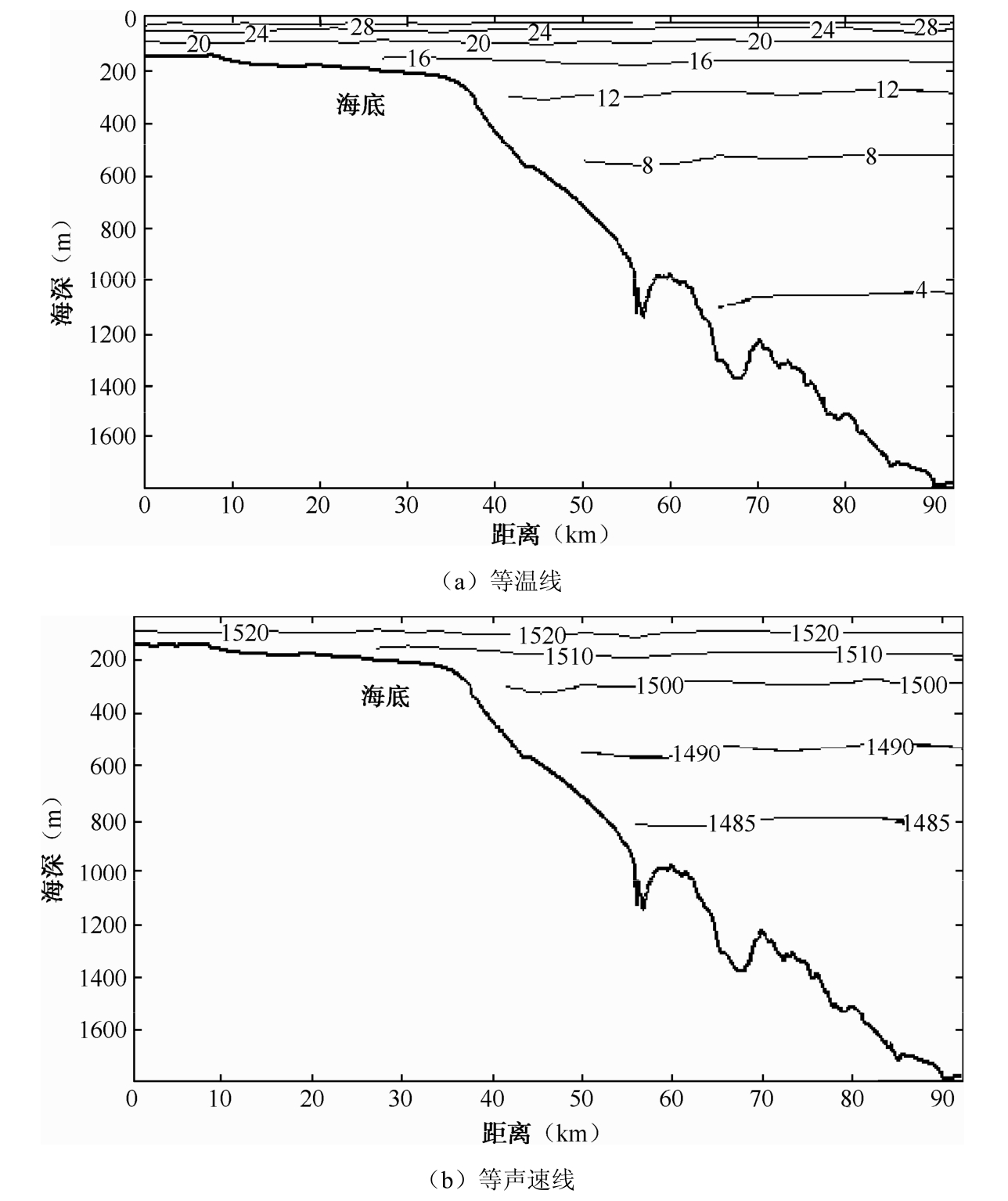
图2.3 典型海区的温度和声速水平分层结构
相对于水平方向而言,声速在垂直方向的分布则具有明显的梯度变化。声速随水深在垂直方向上的变化曲线称为声速剖面,如图2.4(b)所示为典型中纬度深海区域的声速剖面。
由图2.4(b)可以看出,声速剖面可分为三层结构,与相应的图2.4(a)所示的水温剖面相对应。在近表层,由风浪搅拌作用形成的水温较为均一的水层称为混合层,层中声速因压力随深度增大而呈较弱的正梯度结构。混合层的厚度一般随季节呈现出明显的变化,冬季混合层较深,夏季由于季节性温跃层的出现导致混合层变浅。
混合层以下是温跃层,层中水温随深度迅速减小,声速也在一定深度范围内呈现出明显的负梯度结构(即声速值随深度增加而降低)。
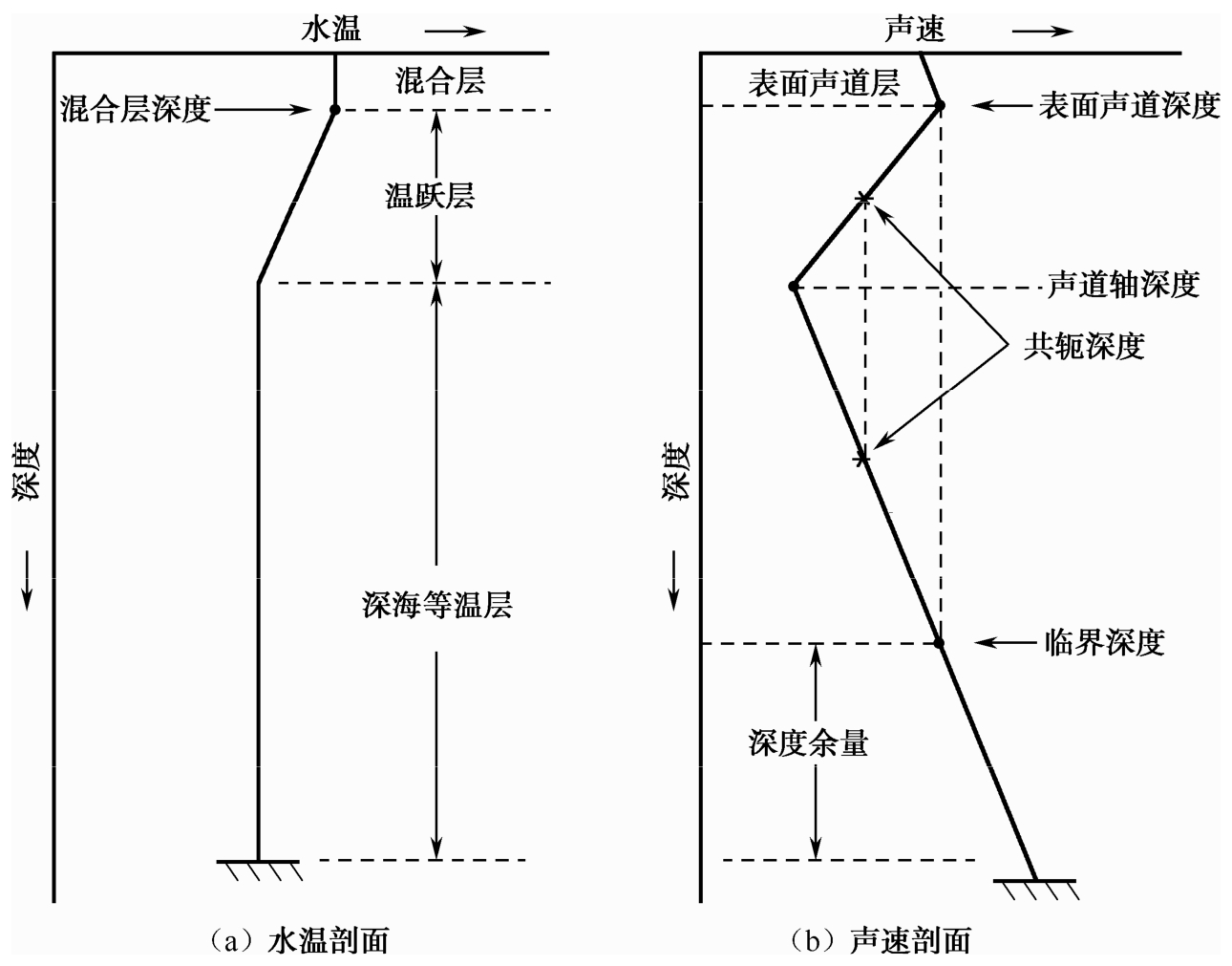
图2.4 典型中纬度深海水温与声速剖面的结构对比
温跃层以下声速最小值所在深度为声道轴的位置。如图2.5所示为Munk和Forbes(1989)给出的全球海洋中的声道轴深度和声速分布。
由图2.5可见,海洋中的声道轴位置一般较为稳定,从赤道到极地逐渐变浅,在中、低纬海区约为几百米到上千米的范围,而在高纬度海区则几乎延伸到海面附近。
声道轴以下的深海中水温、盐度随深度变化很小,称为深海等温层,层中声速因压力随深度增加而近似于线性增大,呈正梯度结构(声速梯度约为0.015~0.020m/s)。在声道轴两侧,往往有两个不同的深度对应同一声速值,称为共轭深度。在声道轴之下,声速值等于近表层声速极大值的深度称为临界深度,临界深度与海底之间的垂直距离称为深度余量。
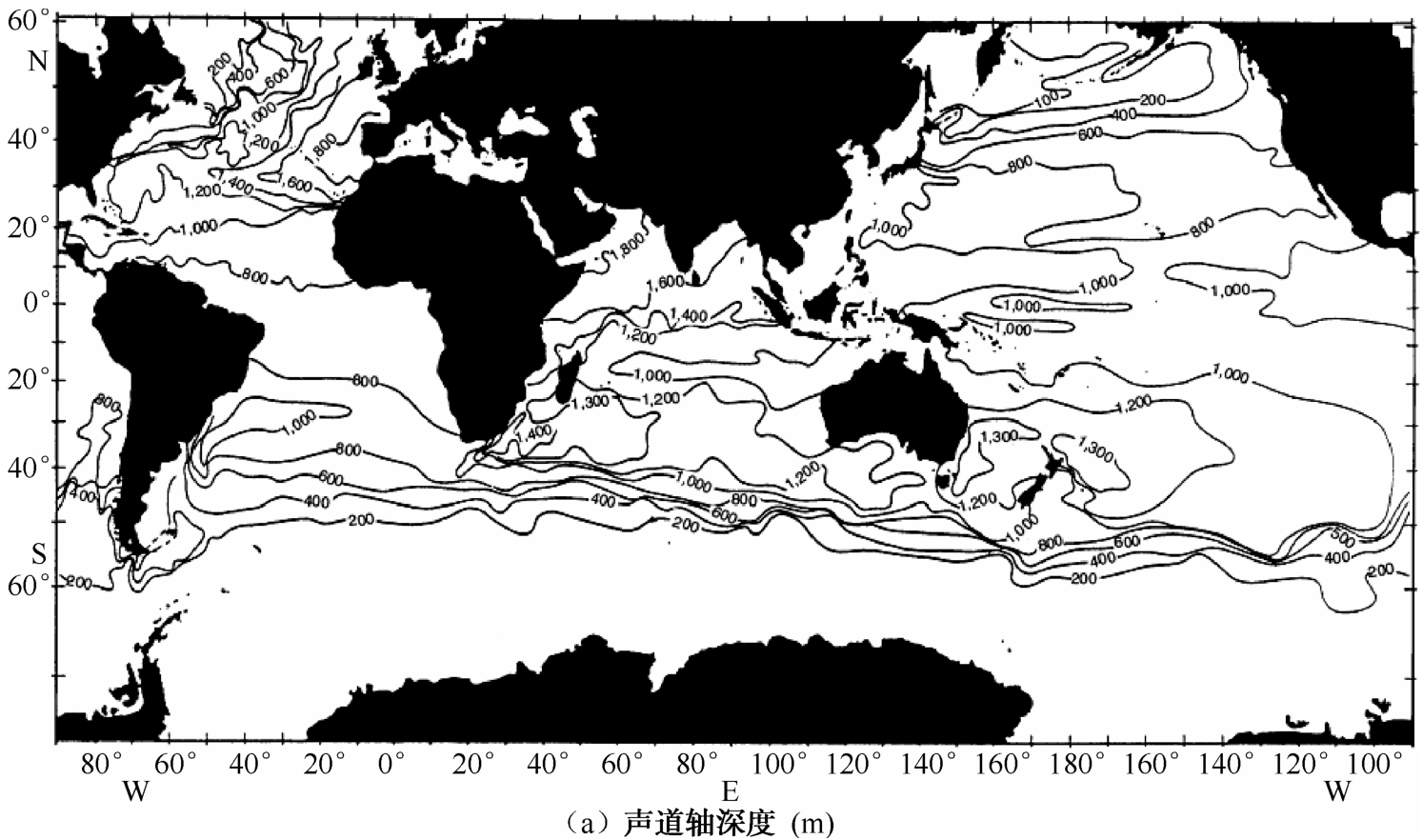
图2.5 全球海洋中的声道轴深度和声速分布(Munk和Forbes,1989)
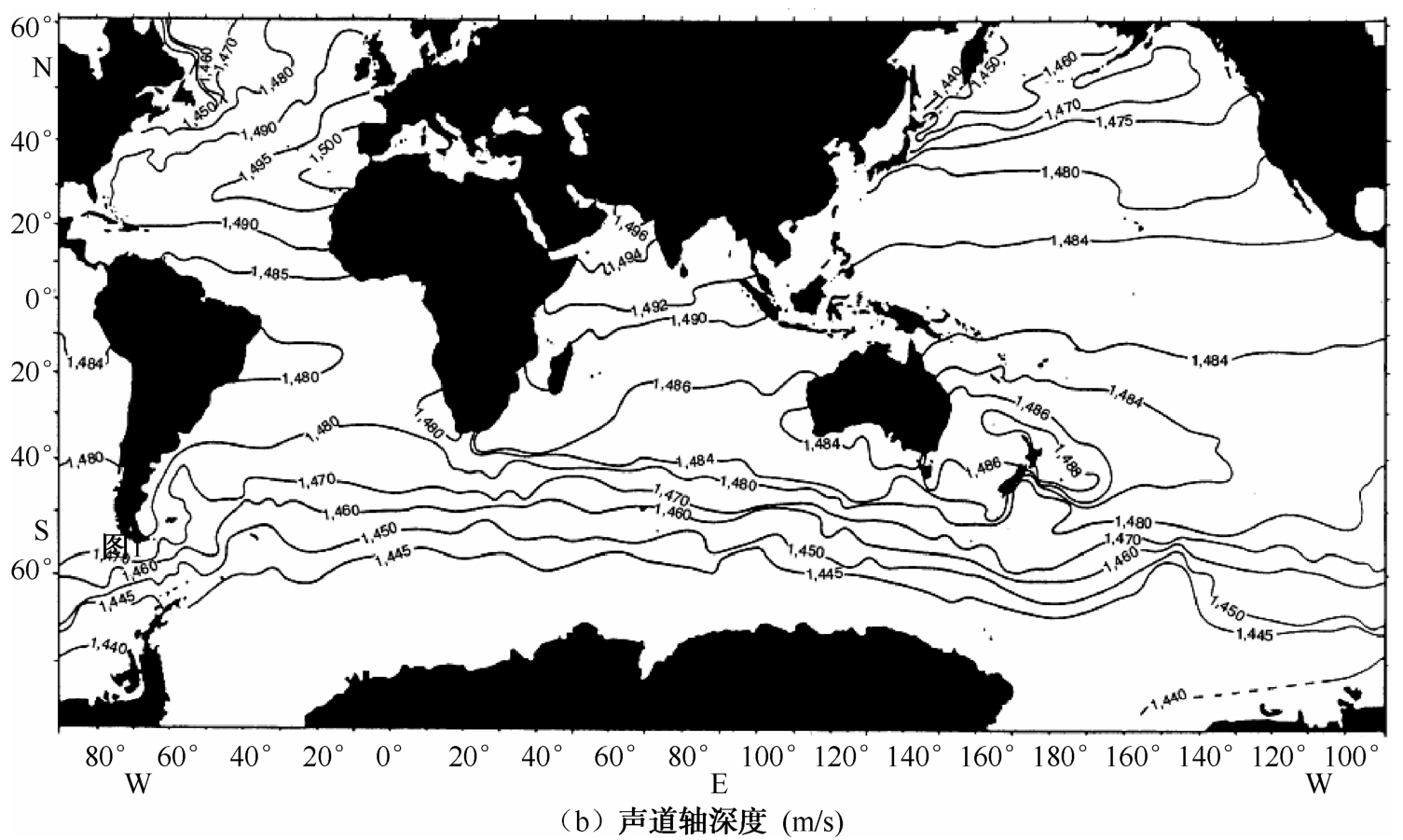
图2.5 全球海洋中的声道轴深度和声速分布(Munk和Forbes,1989)(续)
如图2.6所示,给出了一些典型深海海区冬季的声速剖面结构。可见,真实海洋中的声速剖面结构并没有图2.4描述的那么简单,而是与具体海域的海洋环流和水文环境有关。
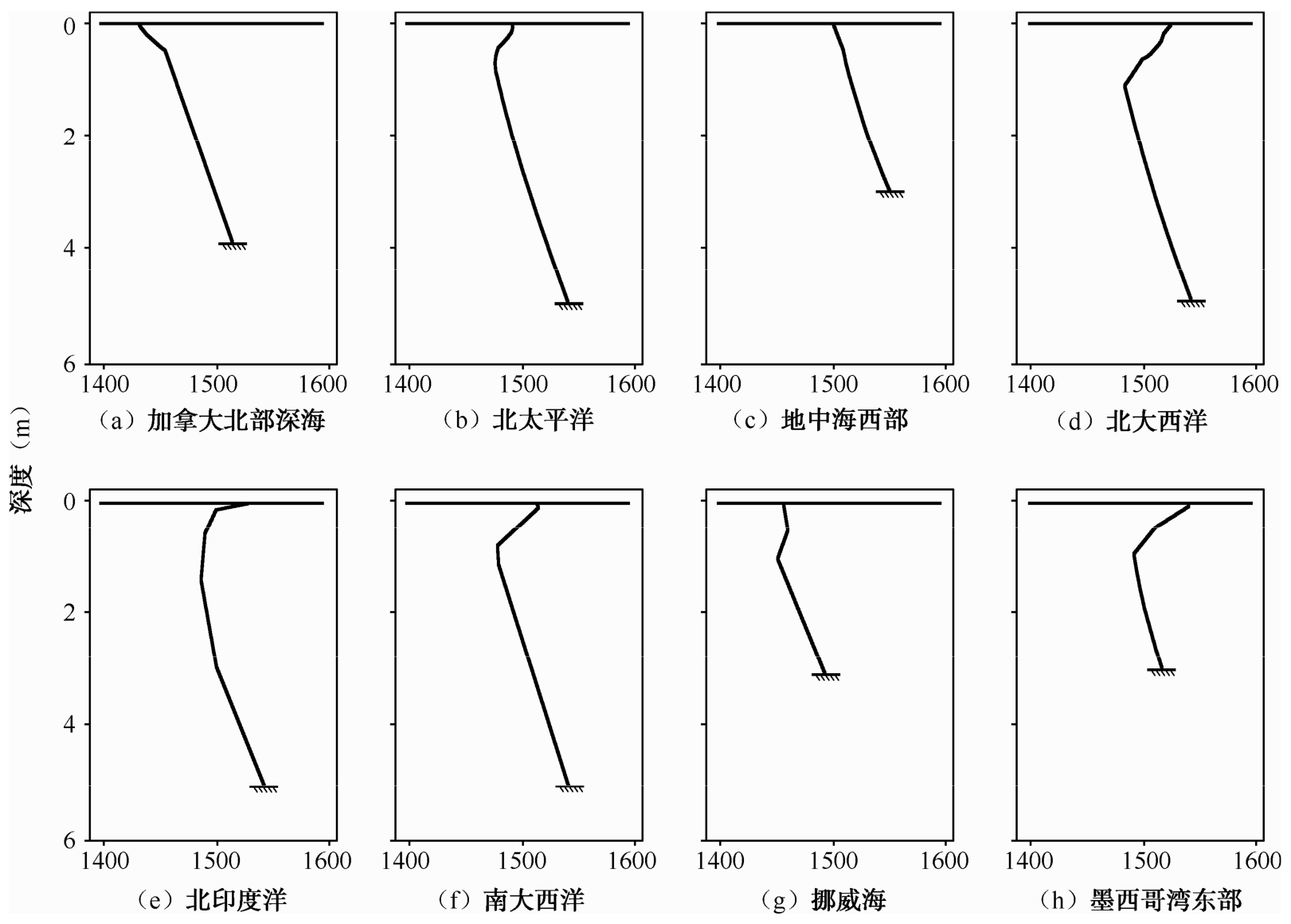
图2.6 典型深海海区冬季的声速剖面结构(Etter,2003)
浅海声速剖面与深海声速剖面有很大不同,受到更多因素的影响,变化较大。在温带浅海大陆架区域,水温和声速结构往往具有明显的季节性特征:在冬季,混合层一般比较深,形成等均匀声速结构或正梯度结构的声速剖面;在春、夏、秋三季,则出现不同程度的季节性跃层,因而出现负梯度结构或温跃层结构的声速剖面。如图2.7所示,给出了北黄海中部区域各个月份的声速剖面结构比较。
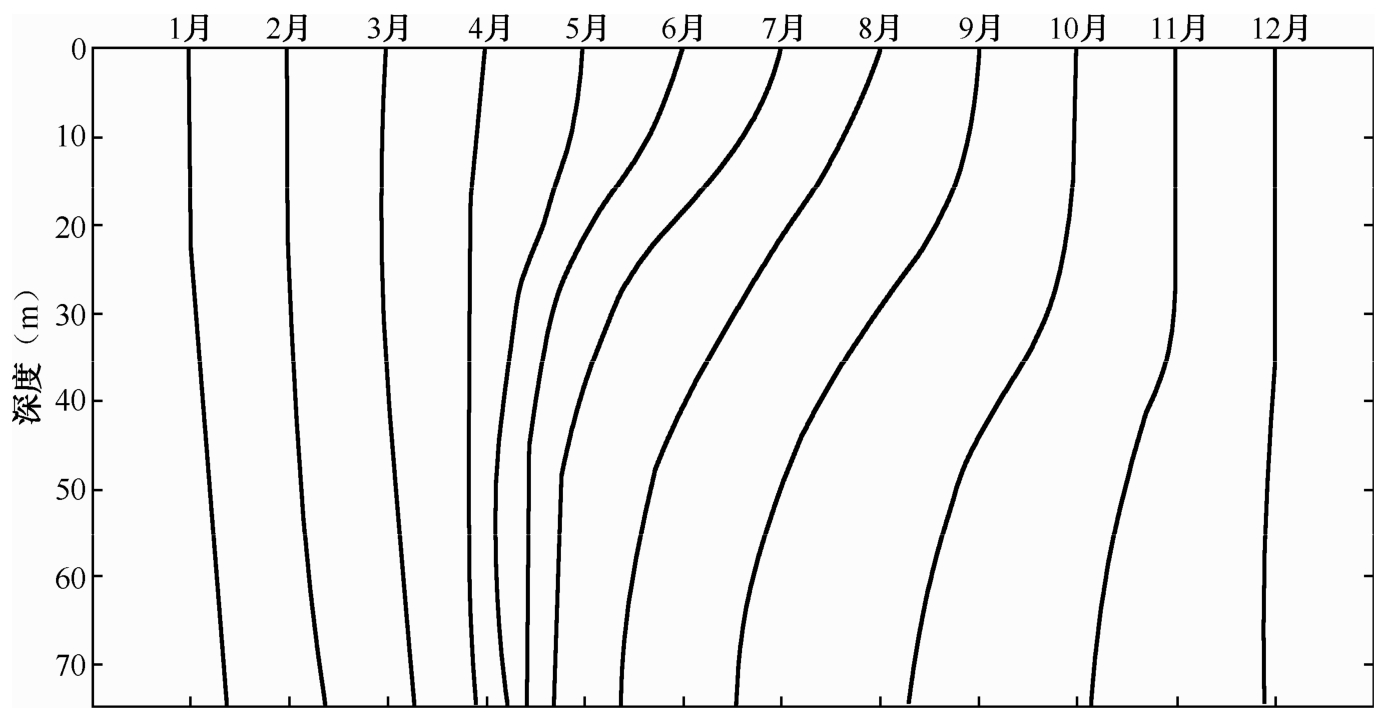
图2.7 北黄海中部区域各个月份的声速剖面结构比较图
在主要海流、上升流和下降流等区域,在冷、暖水团的交汇地带,海水温度、盐度,以及声速会产生明显的水平梯度,即不再呈现水平分层结构。如图2.8所示,给出了一个北大西洋湾流冷环的例子,图中上涌的冷水使水温场出现了明显的水平非均匀分布。
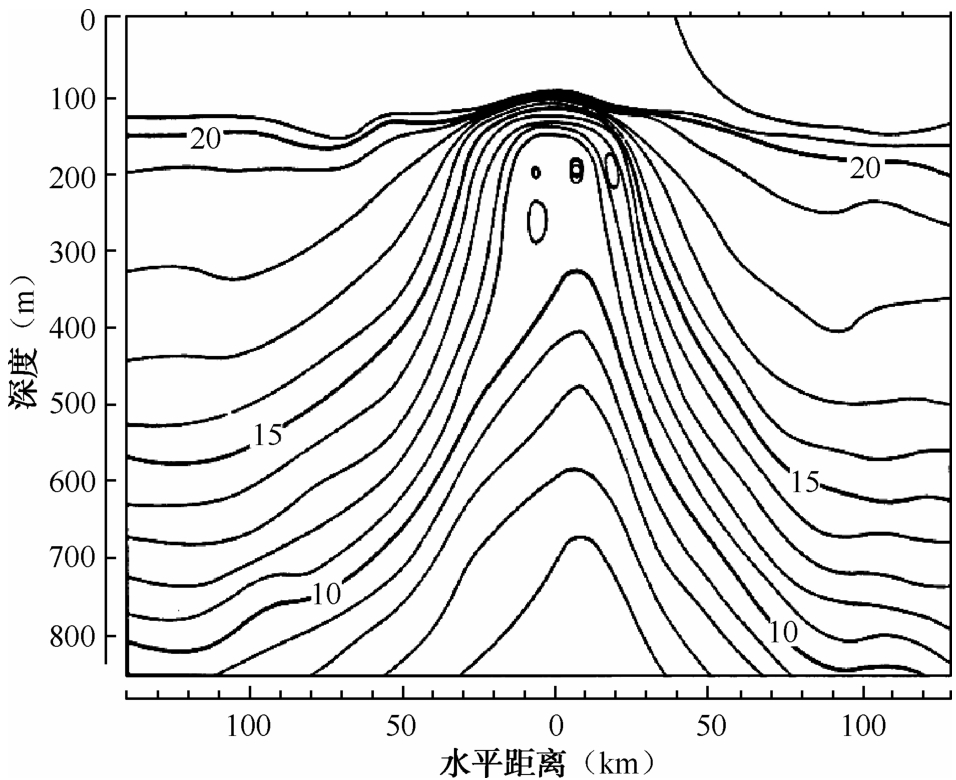
图2.8 北大西洋湾流冷环的典型水温分布(Lai和Richardson,1977)
声波在海水中传播的能量度量参数是声强(I),它通常表示为单位面积上声压的通量,即

式中 p——平面波的声压振幅;
ρ——海水密度;
c——海水声速(乘积ρc通常称为声阻抗)。
传播损耗(TL)描述了声能衰减程度,定义为距离声源1m处的参考声强(I ref )与远处某一点的声强(I)之比,常用对数10倍的形式表示,即

传播损耗随距离而变化,通常有球面扩展和柱面扩展两种方式,如图2.9所示。在不考虑吸收效应的条件下,球面扩展往往适用于深海声传播,而柱面扩展通常适用于浅海环境。
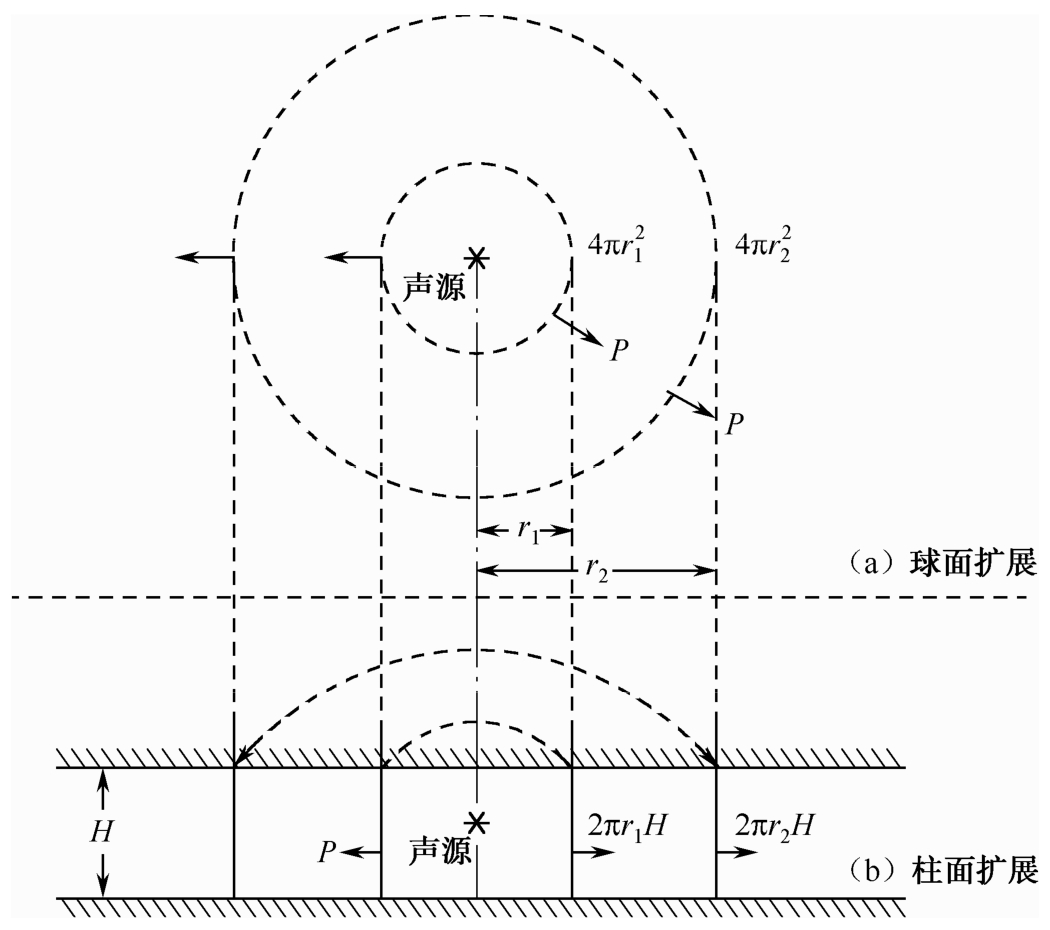
图2.9 球面扩展与柱面扩展示意图
将声强I表示为声功率(P)和面积(A)的关系,即

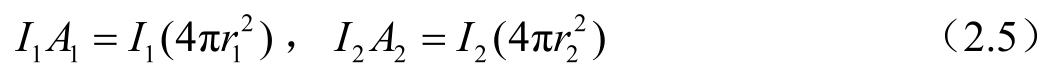
式中 r 1 、r 2 ——分别为两个同心球截面的半径。
由于功率守恒,即P=I 1 A 1 =I 2 A 2 ,因此有

可见,由于球面面积随半径的平方增大,声强随半径的平方的倒数缩小。若以r 1 作为参考单位的距离,则传播损耗为
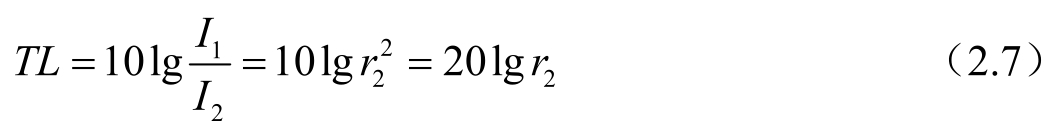
由于海水是均匀的,且边界是理想的反射体,则有

式中 H——波导厚度或水柱的高度。
根据功率守恒,因此有

若以r 1 作为参考单位的距离,则传播损耗为

由式(2.7)和式(2.11)可以看出,柱面和球面扩展条件下的声传播可分别表示为10倍和20倍对数形式的扩展。在理想介质条件下,其他类型的扩展也可简单地表示为这种对数形式,即

式中 r——距离;
n——扩展参数,n取不同值时代表不同类型的扩展。
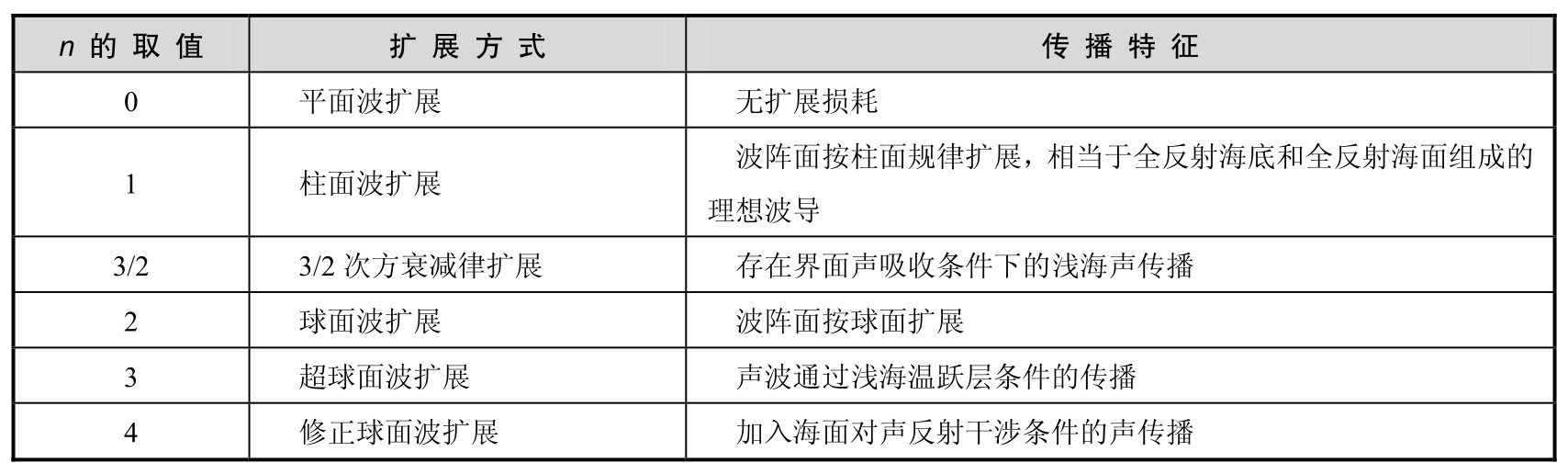
表2.2对不同系数的扩展类型进行了总结。
表2.2 理想介质条件下不同扩展参数的传播特征
声波在介质中的衰减通常是由指数形式e -αx 表示,其中α为衰减系数,单位为(Np/m)。利用以下关系式,可以把声衰减的单位转换成(dB/m),即
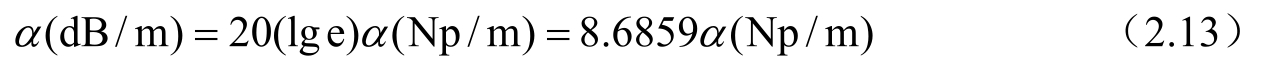
有些传播模型,要求衰减单位为(dB/λ),转化关系为

声波的衰减系数与频率有较大关系,通常由系数k和频率 f 的幂函数表示,即

其中:f 的单位为kHz。通常情况下,衰减系数α可近似为频率的线性函数。
海水中的声吸收是声波在传播过程中声能逐渐损耗转变为热能的一种效应,通常由吸收系数α来表征(dB/km)。吸收系数与海水成分、温度、压力、声波频率及传播方式有关,如图2.10所示,给出了海面4℃海水的吸收系数随频率的变化关系。由图2.10可见,在100 000Hz以下,声吸收主要是由海水中的硼酸离子和硫酸镁离子的弛豫效应引起的;超过100 000Hz,声吸收主要是由介质的黏滞性引起的附加吸收。
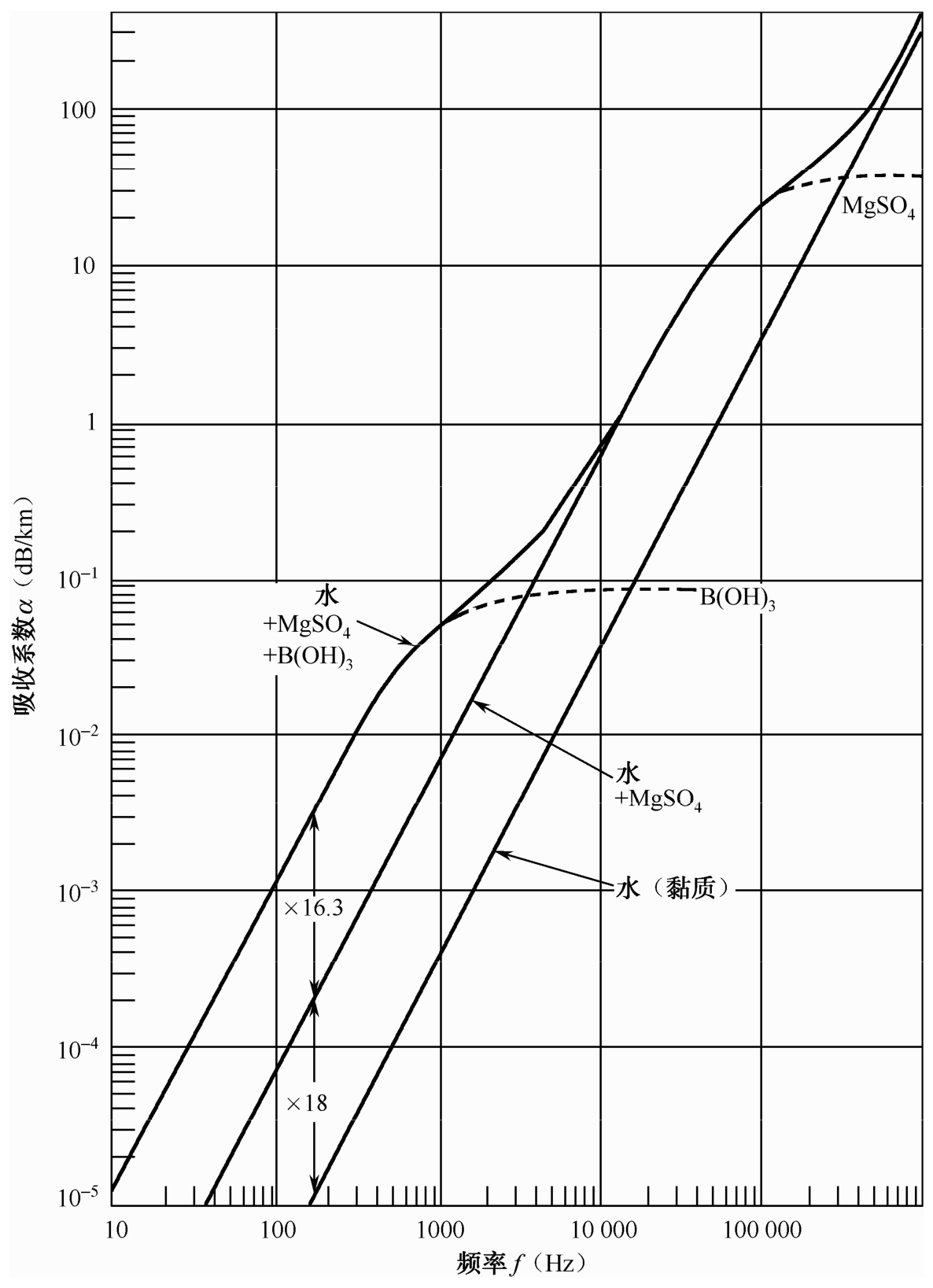
图2.10 海面4℃海水的吸收系数随频率的变化关系(Fisher和Simmons,1977)
注:虚线表示弛豫过程导致的吸收
Thorp(1967)根据不同调查者的许多次测量数据,给出了吸收损耗随频率变化的关系,即
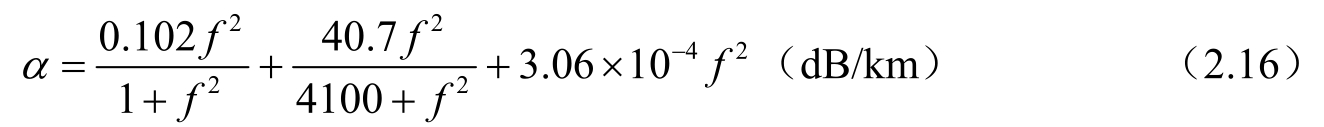
式中 f——声波频率,单位kHz。
由式(2.16)可看出,吸收损耗与频率密切相关,频率提高,吸收损耗迅速增大。
此外,吸收系数随压强的增加而减小,海深为H处的海水吸收系数α H 可表示为

式中 H——水深(m);
α 0 ——海面处海水的吸收系数。
由式(2.17)可见,海水深度每增加1000m,吸收系数就减小6.7%。