下载掌阅APP，畅读海量书库
立即打开
一、问题求解（本大题共15小题，每小题3分，共45分，在每小题的五个选项中选择一项）
1．关于 x ， y 的方程 ax ＋ by ＝2和 ax － by ＝2有相同的解 x ＝－1， y ＝－1，则 a ， b 的值为（ ）
（A）（2，－3） （B）（－2，－3） （C）（2，3）
（D）（－2，0） （E）（0，－2）
2．设实数 x ， y ， z 是三个连续的负整数，并且 x ＞ y ＞ z ，则下列表达式中一定为正奇数的是（ ）
（A） yz － x （B）（ x － y ）（ y － z ） （C） x － yz
（D） x （ y ＋ z ） （E）（ x ＋ y ）（ y － z ）
3．某国对居民月收入实行下列税收方案：不超过3 000美元的部分按 x %税率征收，超过3 000美元但不超过6 000美元的部分按 y %税率征收，超过6 000美元的部分按 z %税率征收，其中 x 、 y 、 z 均为正整数，且 x ＜ y ＜ z ，照此方案，若月收入为4 500美元，则需纳税60美元；若月收入为6 500美元，则需纳税120美元．现某人月收入为10 000美元，则需纳税（ ）美元
（A）260 （B）280 （C）300 （D）330 （E）350
4．甲仓存粮45吨，乙仓存粮141吨，以后甲仓每天存入7吨，乙仓每天运出5吨，（ ）天后甲仓存粮与乙仓相等
（A）8 （B）7 （C）9 （D）6 （E）12
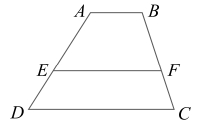
5．如图，梯形 ABCD 中， AB ／／ CD ，且 CD ＝3 AB ， EF ／／ CD ， EF 将梯形 ABCD 分成面积相等的两部分，则 AE ∶ ED ＝（ ）
6．等差数列｛ a n ｝中，若 a 4 ＋ a 6 ＋ a 8 ＋ a 10 ＋ a 12 ＝120，则2 a 10 － a 12 的值为（ ）
（A）20 （B）22 （C）24 （D）26 （E）28
7．4个不同的小球放入甲、乙、丙、丁4个盒中，恰有1个空盒的放法有（ ）种
（A）64 （B）77 （C）124 （D）144 （E）288
8．多项式
x
2
－
xy
－6
y
2
－
x
＋13
y
－6＝（
x
＋
ay
＋
m
）（
x
－
by
＋
n
），则
＝（ ）
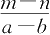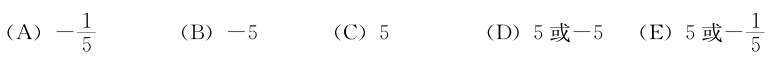
9．一束光线从点 A （－1，1）出发经 x 轴反射，到达圆 C ：（ x －2） 2 ＋（ y －3） 2 ＝1上一点的最短路程是（ ）
（A）4 （B）5 （C）
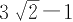（D）
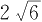（E）6
10．某种酒精溶液里纯酒精与水的比是1∶2，现加进纯酒精120克后，配成浓度为75%的酒精溶液，则原有酒精溶液为（ ）克
（A）70 （B）71 （C）72 （D）73 （E）74
11．已知直线 l 1 的方程为2 x － y ＋1＝0，直线 l 2 与 l 1 关于原点对称，直线 l 3 与 l 2 关于 y ＝ x 对称，直线 l 4 与 l 3 关于 y 轴对称，则 l 4 必过点（ ）
（A）（－3，1） （B）（－3，－1） （C）（－1，3）
（D）（3，－1） （E）（4，－1）
12．已知 a 1 ，…， a k 是有限项等差数列，且 a 4 ＋ a 7 ＋ a 10 ＝17， a 4 ＋ a 5 ＋…＋ a 14 ＝77，若 a k ＝13，则 k 的值是（ ）
（A）18 （B）12 （C）9 （D）22 （E）36
13．若 x 3 ＋ mx 2 －10 x ＋ n 除以 x ＋1余16，除以 x ＋3余18，则（ ）
（A） m ＝2， n ＝4 （B） m ＝－2， n ＝6 （C） m ＝1， n ＝4
（D） m ＝1， n ＝6 （E） m ＝－2， n ＝4
14．某服装公司就消费者对红、黄、蓝三种颜色的偏好情况进行市场调査，共抽取了40名消费者，发现其中有20人喜欢红色，20人喜欢黄色，15人喜欢蓝色，至少喜欢两种颜色的有19人，喜欢三种颜色的有3人，则三种颜色都不喜欢的有（ ）人
（A）8 （B）7 （C）6 （D）5 （E）3
15．袋内装有35个球，每个球上都记有从1到35的一个号码，设号码为
n
的球重
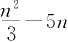＋20克，这些球以等可能性从袋中取出（不受重量和号码等因素的影响），如果任意取出2个球，则它们的重量相等的概率为（ ）
二、条件充分性判断（本大题共10小题，每小题3分，共30分）
解题说明：本大题要求判断所给出的条件能否充分支持题干中陈述的结论．阅读条件（1）和（2）后选择．
A．条件（1）充分，但条件（2）不充分．
B．条件（2）充分，但条件（1）不充分．
C．条件（1）和（2）单独都不充分，但条件（1）和（2）联合起来充分．
D．条件（1）充分，条件（2）也充分．
E．条件（1）和（2）单独都不充分，条件（1）和（2）联合起来也不充分．
16． ab ≥ a ＋ b ．
（1） a ≥2， b ≥2
（2）
17．一个袋子中有4种不同颜色的球，其中红球7个，蓝球9个，黄球8个，白球7个．某人闭上眼睛从中取出 k 个球，可保证4种颜色的球都有．
（1） k ＝25
（2） k ＝26
18． x －2是多项式 f （ x ）＝ x 3 ＋2 x 2 － ax ＋ b 的因式．
（1） a ＝1， b ＝2
（2） a ＝2， b ＝3
19．方程 x 2 ＋ y 2 ＋4 mx －2 y ＋5 m ＝0的曲线是圆．
（1） m ＜0或 m ＞1
（2）1＜ m ＜2
20．
，则
m
＝－6．
（1）（ x ， y ）为直线 x ＋ y ＝1上的点
（2）（ x ， y ）为直线 x ＋2 y ＝0上的点
21．三角形的内切圆的面积与外接圆的面积的比值为
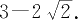
（1）等腰三角形
（2）直角三角形
22．在长方体的体对角线和面对角线中任取两条，这两条恰好是面对角线的概率是 p ．
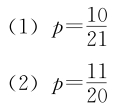
23．将数字1，2，3，4，5，6从左到右排成一列，记第 i 个数为 a i （ i ＝1，2，…，6），若 a 1 ≠1， a 3 ≠3， a 5 ≠5，则不同的排列方法种数为30．
（1） a 1 ＜ a 3 ＜ a 5
（2）0．4≤ p ≤0．8； a 5＜ a 3＜ a 1
24．两直线 l 1 ：（ m －1） x ＋ y ＋2＝0， l 2 ：（ m 2 ＋3 m －4） x ＋（2 m ＋5） y ＋ m ＝0互相平行．
（1） m ＝1
（2） m ＝－1
25． A ＋ B ＝1．
（1）甲、乙两个射手的命中率分别为0．7和0．5，现两人各射击一次，恰有1人命中的概率为 A
（2）同时抛3枚均匀硬币，出现正面向上为奇数枚的概率为 B