





在日常的生活当中,人们习惯用十进制来表示数,但计算机只能识别二进制数。二进制是计算机中数制的基础。
按进位的原则进行计数,称为进位计数制,简称“数制”。数制有多种,在计算机中常用的有十进制数、二进制数和十六进制数。
(1)十进制数
按“逢十进一”的原则进行计数,它的基数为“十”,所使用的数码为 0~9共 10个数字。对于任意4位十进制数,都可以写成如下形式:
D 3 D 2 D 1 D 0 =D 3 ×10 3 +D 2 ×10 2 +D 1 ×10 1 +D 0 ×10 0
式中,D 3 、D 2 、D 1 、D 0 称为数码;10为基数;10 3 、10 2 、10 1 、10 0 是各位数码的“位权”,该式称为按位权展开式。
例:30681 = 3×10 4 +0×10 3 +6×10 2 +8×10 1 +1×10 0
(2)二进制数
按“逢二进一”的原则进行计数,它的基数为“二”,其使用的数码只有 0和 1两个。二进制数在计算机中容易实现,可以用电路的高电平表示“1”,低电平表示“0”。或者用三极管截止时集电极的输出表示“1”,导通时集电极输出表示“0”。
对于任意一个4位二进制数,都可以写成如下形式:
B 3 B 2 B 1 B 0 = B 3 ×2 3 +B 2 ×2 2 +B 1 ×2 1 +B 0 ×2 0
式中,B 3 、B 2 、B 1 、B 0 称为数码;2为基数;2 3 、2 2 、2 1 、2 0 是各位数码的“位权”。
例:(1101) 2 =1×2 3 +1×2 2 +0×2 1 +1×2 0 =13
由于二进制运算实行的借进位规则是“逢二进一,借一当二”,因此二进制的运算规则相当简单。
加法:0+0=0;0+1=1;1+0=1;1+1=10
减法:0-0=0;1-0 =1;1-1=0;10-1=1
乘法:0×0=0;0×1= 0;1×0=0;1×1=1
除法:0÷1=0;1÷1=1
例:求(1101) 2 ×(101) 2 的值。
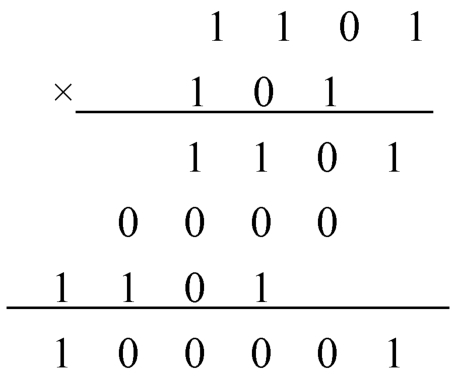
因此,可得(1101) 2 ×(101) 2 =(100001) 2
(3)十六进制数
由于二进制位数太长,不易记忆和书写,因此人们又提出了十六进制的书写形式。在单片机的C语言程序设计中经常用到十六进制数。
按“逢十六进一”的原则进行计数,它的基数为“十六”,所使用的数码共有 16个:0、1、2、3、4、5、6、7、8、9、A、B、C、D、E和F。其中,A、B、C、D、E和 F所代表的数的大小相当于十进制的 10、11、12、13、14和 15。对于任意 4位一个十六进制数,都可以写成如下形式:
H 3 H 2 H 1 H 0 = H 3 ×16 3 +H 2 ×16 2 +H 1 ×16 1 +H 0 ×16 0
式中,H 3 、H 2 、H 1 、H 0 称为数码;16为基数;16 3 、16 2 、16 1 、16 0 是各位数码的“位权”。
例:(120B) 16 =1×16 3 +2×16 2 +0×16 1 +11×16 0 =4619
将一个数由一种数制转换成另一种数制称为数制间的转换。
(1)十进制数转化为二进制数
十进制数转化为二进制数采用“除2取余法”,即将十进制数依次除以2,并依次记下余数,一直除到商为0,最后把全部余数按相反次序排列,就能得到二进制数。
例:把十进制数45转化为二进制数。
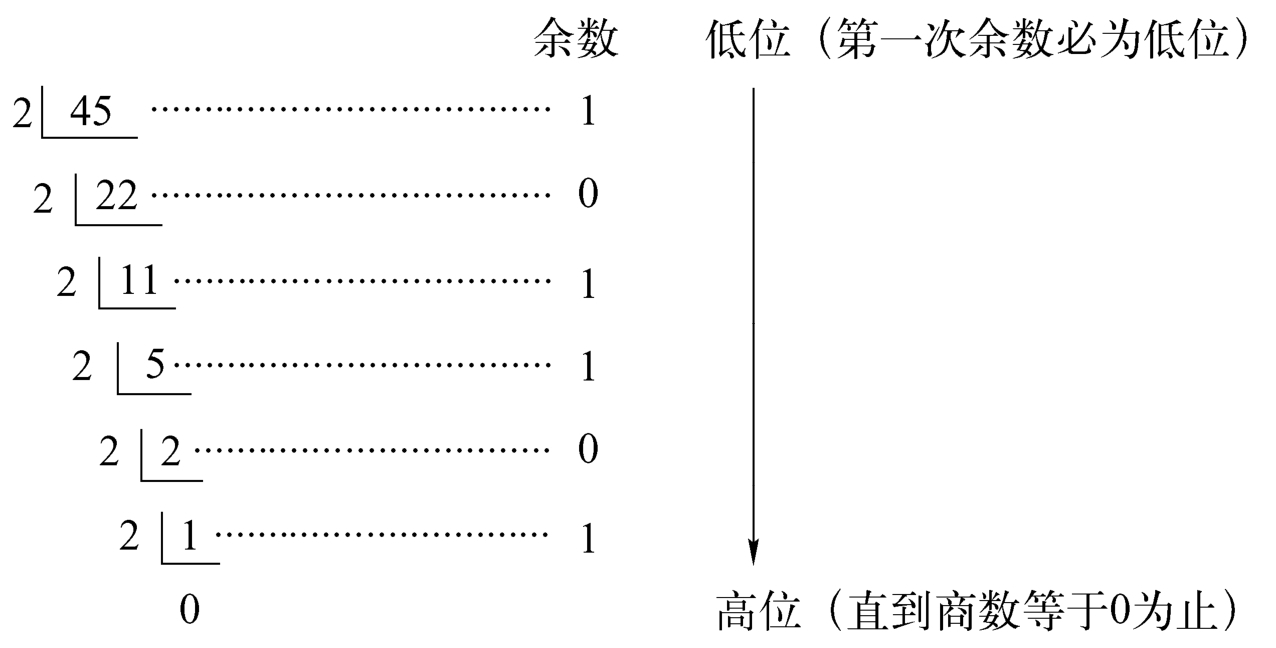
因此可得45=(101101) 2
(2)二进制数转化为十进制数
二进制数转化为十进制数采用“位权法”,即把各非十进制数按位权展开,然后求和。
例:把(1011) 2 转化为十进制数。
(1011) 2 =1×2 3 +0×2 2 +1×2 1 +1×2 0 =11
(3)二进制数转化为十六进制数
将二进制数转化为十六进制数的规则是,从右向左,每 4位二进制数转化为 1位十六进制数,不足部分用0补齐。
例:把(101101101101) 2 转化为十六进制数。
把(101101101101) 2 写成下面形式:
1011 0110 1101
B 6 D
所以,(101101101101) 2 =(B6D) 16
(4)十六进制数转化为二进制数
十六进制数转化为二进制数的方法是,从左到右将待转换的十六进制数中的每个数码依次用4位二进制数表示。
例:将十六进制数(31AB) 16 转化为二进制数
将每位十六进制数写成4位二进制数,即
3 1 A B
0011 0001 1010 1011
因此可得,(31AB) 16 =(0011000110101011) 2
为了便于书写,特别是方便编程时书写,规定在数字后加一个字母以示区别。二进制后加B;十六进制后加H;十进制后面加D,其中D可以省略。
例:3BH=00111011B=59D=59
表 1-1列出了常用数值的各种数制间的对应关系。这在单片机 C语言程序设计中经常用到,需要熟练掌握。
表1-1 常用数制的对应关系
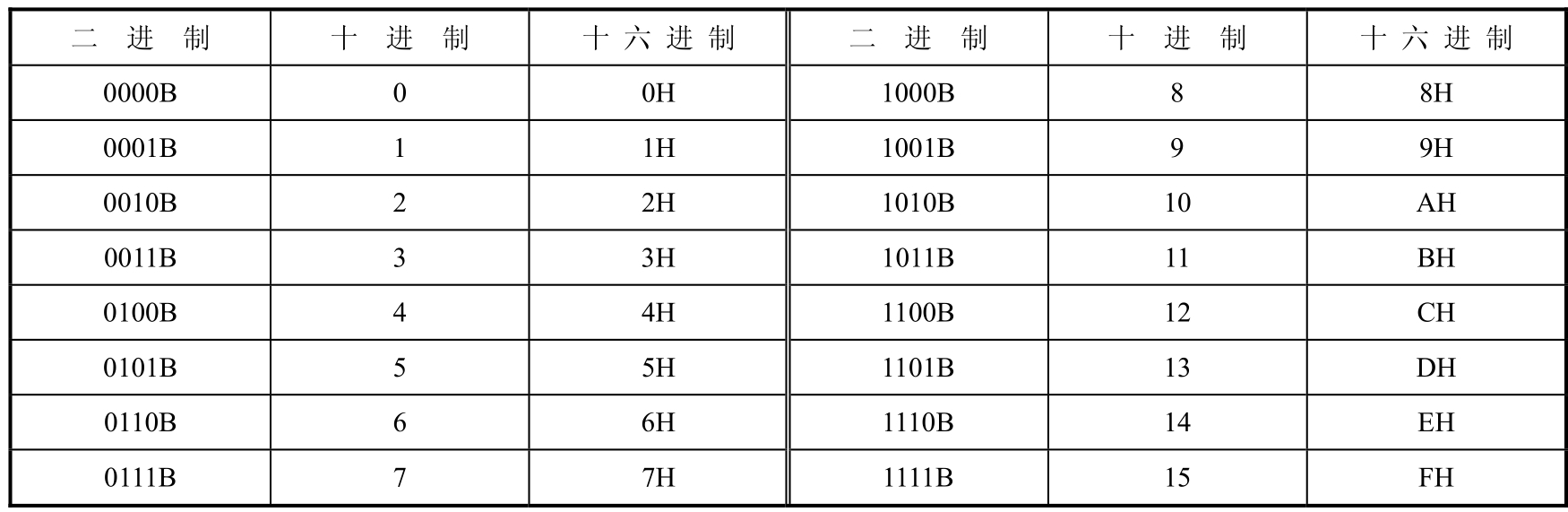
为了使计算机具有逻辑判断能力,就需要逻辑数据,并能对它们进行逻辑运算,得出一个逻辑式的判断结果。每个逻辑变量或逻辑运算的结果产生逻辑值,该逻辑值只能取“真”或“假”两个值。判断成立时为“真”,判断不成立时为“假”。在计算机内常用“0”和“1”表示这两个逻辑值,“0”表示假,“1”表示真。因此,在逻辑电路中,输入和输出只有两种状态,即高电平“1”和低电平“0”。
最基本的逻辑运算有逻辑“与”、逻辑“或”及逻辑“非”3种。
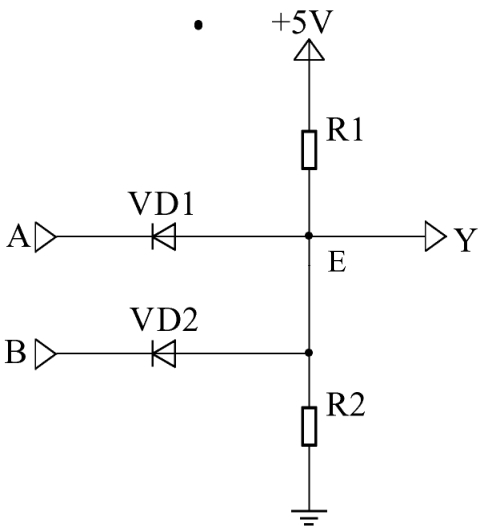
图1-5 二极管与电阻构成的逻辑“与”电路
逻辑“与”也称之为逻辑乘,最基本的“与”运算有两个输入量和一个输出量。图 1-5所示为二极管与电阻构成的逻辑“与”电路。其中,A、B为输入端,Y为输出端,+5V电压经R1、R2分压,在E点得到+3V的电压。
(1)逻辑“与”的实现原理
当A、B两端同时输入低电平(0V)时,由于E点电压为 3V,因此,二极管 VD1、VD2都导通,E点电压马上降到 0.7V(低电平)。也就是说,当 A、B两端同时输入低电平“0”时,Y端输出低电平“0”。
当A端输入低电平(0V),B端输入高电平(5V)时,由于E点电压为3V,因此,二极管VD1马上导通,E点电压马上降到0.7V(低电平),而二极管VD2处于截止状态。此时,Y端输出低电平“0”。
当A端输入高电平(5V),B端输入低电平(0V)时,二极管VD1截止,二极管VD2则处于导通状态,E点仍为0.7V(低电平)。此时,Y端输出低电平“0”。
当A、B两端同时输入高电平(5V)时,二极管VD1、VD2都不能导通,E点电压为3V(高电平)。此时,Y端输出高电平“1”。
由此可见,只有当输入端均为高电平时,输出端才会输出高电平;只要有一个输入端输入低电平,输出端就会输出低电平。这就是逻辑“与”运算的特点。
(2)真值表
真值表列出电路的各种输入值和对应的输出值,可以直观地看出电路的输入与输出之间的关系。表1-2列出了逻辑“与”的真值表。
表1-2 逻辑“与”的真值表
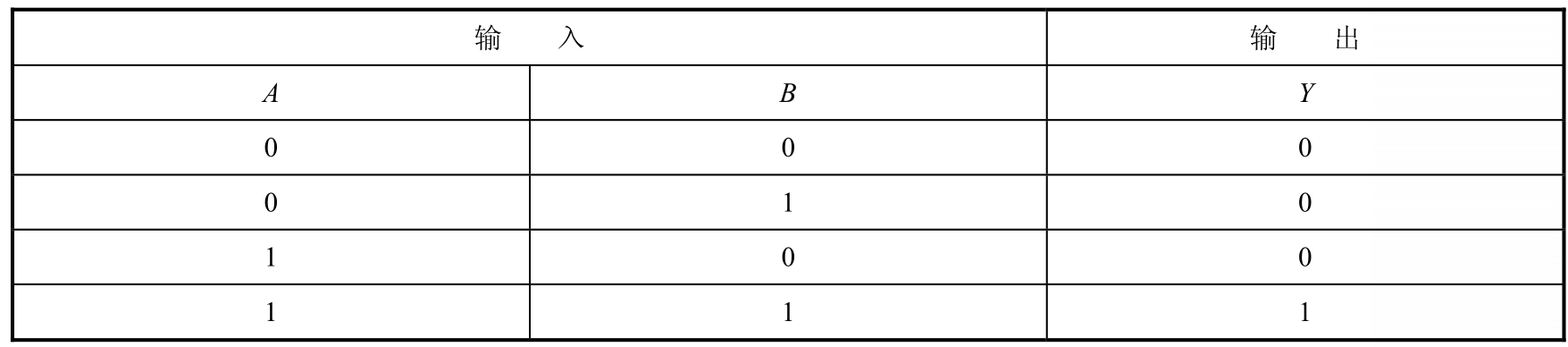
(3)逻辑表达式与运算规则
逻辑“与”的表达式为
Y = A · B
逻辑“与”的运算规则可总结为“有0为0,全1出1”。
逻辑“或”也称为逻辑加,最基本的逻辑“或”运算有两个输入量和一个输出量。它的逻辑表达式为
Y = A + B
逻辑“或”的运算规则可总结为“有1为1,全0出0”。
3.逻辑“非 ”
逻辑“非”即取反,它的逻辑表达式为
Y
=
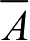
逻辑“非”的运算规则可总结为“1的反为0,0的反为1”。
若在一个逻辑表达式中出现多种逻辑运算,可用小括号指定运算的次序;无小括号时按逻辑“非”、逻辑“与”和逻辑“或”的顺序执行。
下面通过一个例子来说明单片机是如何表示数的。
一盏灯要么“亮”,要么“灭”,只有两种状态。如果规定用灯亮为“1”,灭为“0”,那么一盏灯可以表示的数为0和1,共 2 1 =2个数。
两盏灯可以有“灭灭”、“灭亮”“亮灭”和“亮亮”共 4种状态,即“00”、“01”、“10”和“11”,而二进制数00、01、10和11分别相当于十进制数的0、1、2和3。所以,两盏灯可以表示的数为0、1、2和3,共 2 2 =4个数。
三盏灯的全部状态可以表示为,“000”、“001”、“010”、“011”、“100”、“101”、“110”和“111”,所以,三盏灯可以表示的数为 0、1、2、3、4、5、6和 7,共2 3 =8个数。
同样地,八盏灯一共可以表示 2 8 =256个数。
通过前面的例子可知,一盏灯亮灭或电平的高低可以代表两种状态,即“0”和“1”。实际上这就是一个二进制位。位(Bit)是计算机中所能表示的最小数据单位。
相邻的8位二进制码称为一个字节(Byte),用B表示。字节是一个比较小的单位,常用的还有KB和MB等,它们之间的关系如下:
1MB=1024KB=1024×1024B
字节是计算机内部进行数据处理的基本单位。它由若干位二进制码组成,通常与计算机内部的寄存器、运算器、数据总线的宽度一致。每个字所包含的位数称为字长。若干个字节定义为一个字,不同类型的单片机有不同的字长。8051内核的单片机是 8位机,它的字长为8位,其内部的运算器等都是8位的,每次参加运算的二进制位只有8位。