




 连点找多边形
连点找多边形
让我们从一个实验开始本小节主题。请你在一张纸上任意画5个点,仅要求其中不要有3点共线。请你尝试在这5个点里找4个点连接起来,目标是构成一个凸四边形。
可以尝试在纸上多画几组,你会很快发现,不管怎么画这5个点,似乎总能找出4个点来构成凸四边形。但是很显然,只有4个点的话,不一定能构成凸四边形。如果让你尝试画5个点,其中不存在某4个点的连线可以构成凸四边形,你会发现怎么都做不到。
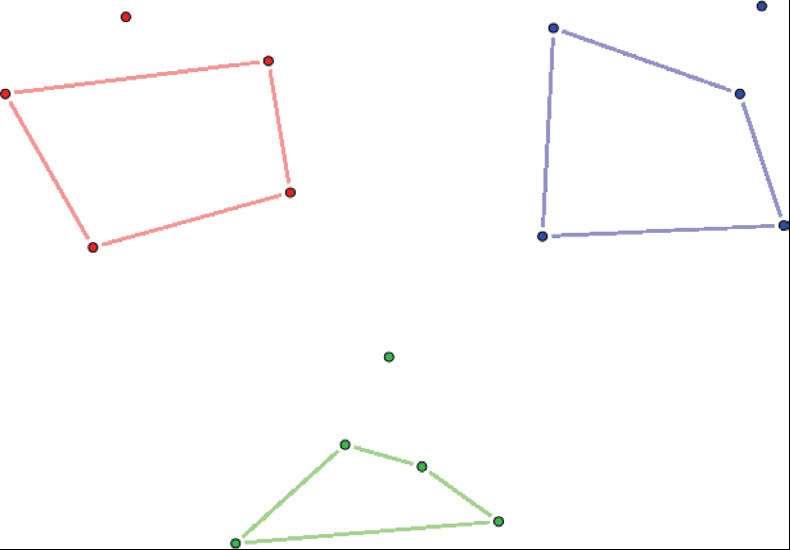
幸福结局问题:平面上任意5个点,似乎总能找出4个点并连线,构成凸四边形。
现在问题是能否证明按如此条件构成凸四边形,是否至少就需要5个点呢?是否存在某种5个点的位置不能构成凸四边形的情况呢?如果要构成凸五边形,又至少需要多少个点呢?凸六边形又如何呢?通常来说,平面上至少需要多少个点来构成凸n边形的问题,就是所谓“幸福结局问题”。
但这跟“幸福结局”有什么关系呢?因为这与一个过程曲折但结局完美的故事有关。大约在1933年,匈牙利首都布达佩斯有一群爱好数学的年轻人,他们经常聚在一起讨论数学问题。其中最为活跃的有三个人:一个女孩子名叫埃丝特·克莱因,当时23岁;比她小一岁的男生乔治·塞凯赖什;还有一个当时20岁的,后来大名鼎鼎的保罗·埃尔德什。
有一天,埃丝特·克莱因拿了一个问题去挑战她的这两个朋友,请他们证明前面提过的例子,是否平面上有5个点,就必然能在其中找到4个点,构成一个凸四边形。没过多久,塞凯赖什和埃尔德什就证明了这一问题。而且两年后,他们两人还证明了,对任何一个凸n边形,只需要最多
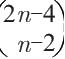 +1个点,肯定就能从其中找到n个点,构成一个凸n边形。这个定理就被称为“埃尔德什 - 塞凯赖什定理”。
+1个点,肯定就能从其中找到n个点,构成一个凸n边形。这个定理就被称为“埃尔德什 - 塞凯赖什定理”。
而让人羡慕的是,塞凯赖什和克莱因在一起研究这个问题的过程中,坠入爱河,最后喜结连理。你看这是不是一个幸福结局呢?所以后来爱开玩笑的埃尔德什就说,这个问题干脆就叫“幸福结局问题”好了。
塞凯赖什夫妇跟中国还有点缘分。他们1937年在匈牙利结婚,两年后“二战”爆发,因为两人都是犹太人,不得不开始逃亡,他们选择逃到了上海,并在上海定居下来。在“二战”期间,上海接收过四万多犹太难民,其中就有这两位数学家。他们在上海居住了9年,第一个孩子也出生在上海,后于1948年移居澳大利亚,并一直生活在那里。更为神奇的是两位数学家都很长寿,活了90多岁,直到2005年,二人在1个小时内相继去世。所以他们的人生绝对称得上是幸福结局。
再顺便说说给这个问题起名为“幸福结局”的埃尔德什,他在数学界更为著名。其最为出名的成就就是多产,一生发表过1500篇论文,且他喜欢与众多数学家合作发表论文。以至于数学界有这样一个非正式学术指标,叫“厄多斯数”,“厄多斯”就是埃尔德什的另一种中文译音,意思是说如果你跟埃尔德什合作发表过论文,那你的厄多斯数就是1。如果你跟厄多斯数为1的人合作发表过论文,那你的厄多斯数就是2,以此类推。当然,厄多斯数越小,在某种程度上说明你的数学水平或者地位越高。现在埃尔德什已经去世,所以各位想成为厄多斯数为1,已经不可能了。各位可以赶紧找找身边有没有厄多斯数的人,你跟他一起发表篇论文,那你就有厄多斯数了。
前面已经说过塞凯赖什和埃尔德什证明了无论几边形,需要的点数总有一个上限的。但数学家就想找到一个准确的数。
埃尔德什和塞凯赖什自己就证明了凸五边形需要9个点。而三角形很明显只要3个点,凸四边形需要5个点。埃尔德什和塞凯赖什根据已知情况猜想,对n边形,需要:
1+2 n-2
个点。以此类推,那凸六边形,就需要17个点等。但即使有了猜想,凸六边形的情况时隔70年,直到2005才被证明,而且还是借助计算机证明的。但对于凸七边形,需要的点数就达到33个,计算机也无能为力。所以对一般情况的处理,数学家只能通过缩小上界的方法,慢慢逼近下限。
1935年,埃尔德什和塞凯赖什证明了上界的存在性,为
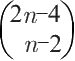 +1,下界就是1+2
n-2
。而他们认为下界就是所需的最少点数。让我们来看看n=4时的命题证明框架:
+1,下界就是1+2
n-2
。而他们认为下界就是所需的最少点数。让我们来看看n=4时的命题证明框架:
如下图,假设在平面上已有5点,并且任意3点不共线。取其中3点构成一个三角形。余下两个点记作 A 、 B ,连接 AB 得到一条直线,如点 A 、 B 都在三角形内,则直线 AB 必交三角形两边,将三角形分为两部分,其中一部分是三角形,另一部分是四边形。在四边形的那一部分,连接 BC 、 AD ,则必可得到一个凸四边形:
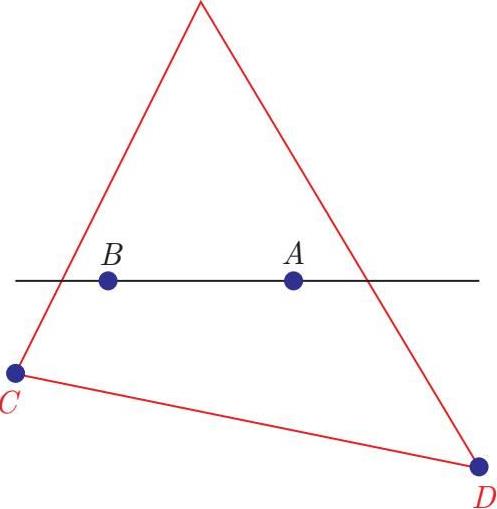
A 、 B 两点在其他三点构成的三角形内,则 ABCD 可以构成一个凸四边形。
如果连接三点构成三角形后,余下两点不全在这个三角形内,则至少有一个点在三角形外,记作 D 。连接原先三角形的3个点和 D ,则也必可得到一个凸四边形:
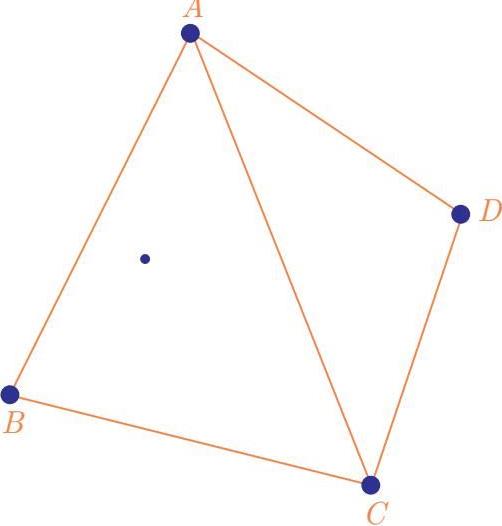
取三角形 ABC 外一点D连线,则 ABCD 构成一个凸四边形。
别看n=4的情况如此“简单”,对n等于任意数的证明却异常困难。据埃尔德什和塞凯赖什说,n=5,f(5)=9的情况,是1935年一个叫E·马凯的人证明的。
n=6,f(6)=17的结果是塞凯赖什(成果发表时已去世)和林赛·彼得斯于2006年证明的。
最新成果是安德鲁·苏克在2016年声称自己证明了上界是f(N)≤
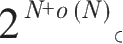 这个结果与最终正确答案只差一步之遥,但还需要验证。
这个结果与最终正确答案只差一步之遥,但还需要验证。
另外值得一提的是,这个幸福结局问题是“拉姆齐理论”的第一个重要的应用。拉姆齐理论是处理这种类似问题的理论——最少需要几个人,使得其中有3个人互相认识或者互相不认识?拉姆齐在20世纪30年代证明这个结果是6个人。但是直到现在,如果问至少需要几个人,使得其中5个人互相认识或者互相不认识,答案是——数学家还不知道!只知道是需要43~48个人。所以拉姆齐理论也是看上去简单,却是数学家解决不了的问题。

平面上有8个点,但无法构成凸五边形的一个例子,即证明f(5)>8。
幸福结局问题有一个扩展,叫“空心幸福结局问题”。它比幸福结局问题多一个要求:构成的凸多边形中不含其他点。目前已知空心幸福结局问题,构成四边形仍然只需5个点,五边形则需10个点。
你可能感觉在空心幸福结局问题中,只要点数多一点就可以了,但是约瑟夫·霍顿在1983年证明,当点数足够多时,可以做到,无论你怎么找,都不能找到空心凸七边形。但是长期以来,有关六边形的空心幸福结局问题的情况不清楚。在2007年和2008年时,有人证明,只要点数足够多,就会有空心凸六边形了,但到29个点时有反例。至于上限,目前知道的是129个点以上都成立。所以问题的答案在29到129之间,具体是哪个数仍未可知。
1.请思考一下为什么幸福结局问题那么难?平面上有17个点,可以连线构成多少个六边形(凹凸不论)?
2.如果平面上有1+2 n-2 个点,可以从中构造多少个n边形?