下载掌阅APP，畅读海量书库
立即打开
根据目标跟踪的定义，目标跟踪的本质是一个混合系统的状态估计问题，即利用传感器的离散量观测来估计目标的连续状态，滤去随机噪声和求解目标运动要素。
在目标跟踪系统中，根据传感器和跟踪处理目标的数量关系，可将目标跟踪问题分为三类：
（1）单传感器单目标跟踪（Single Sensor Single Target Tracking, SST），即单部传感器对单个目标的跟踪处理。
（2）单传感器多目标跟踪（Single Sensor Single Multiple Targets Tracking, SMT），即单部传感器对多个目标的跟踪处理。
（3）多传感器多目标跟踪（Multiple Sensors Multiple targets Tracking, MSMTT），即多部传感器实现多个目标的跟踪处理。
这三类目标跟踪问题中，单传感器单目标跟踪和单传感器多目标跟踪理论和方法是基础。而多传感器多目标跟踪就是利用多传感器的联合探测来实现多目标融合跟踪，它是多传感器信息融合中的热点问题。
单目标跟踪涉及目标坐标系的选择、观测数据预处理、目标运动模型建模、机动检测与机动辨识、滤波与预测等主要步骤，如图1.2所示。与单目标跟踪相比，多目标跟踪还需要考虑数据互联、跟踪门规则、跟踪起始和跟踪终止等内容，如图1.3所示。
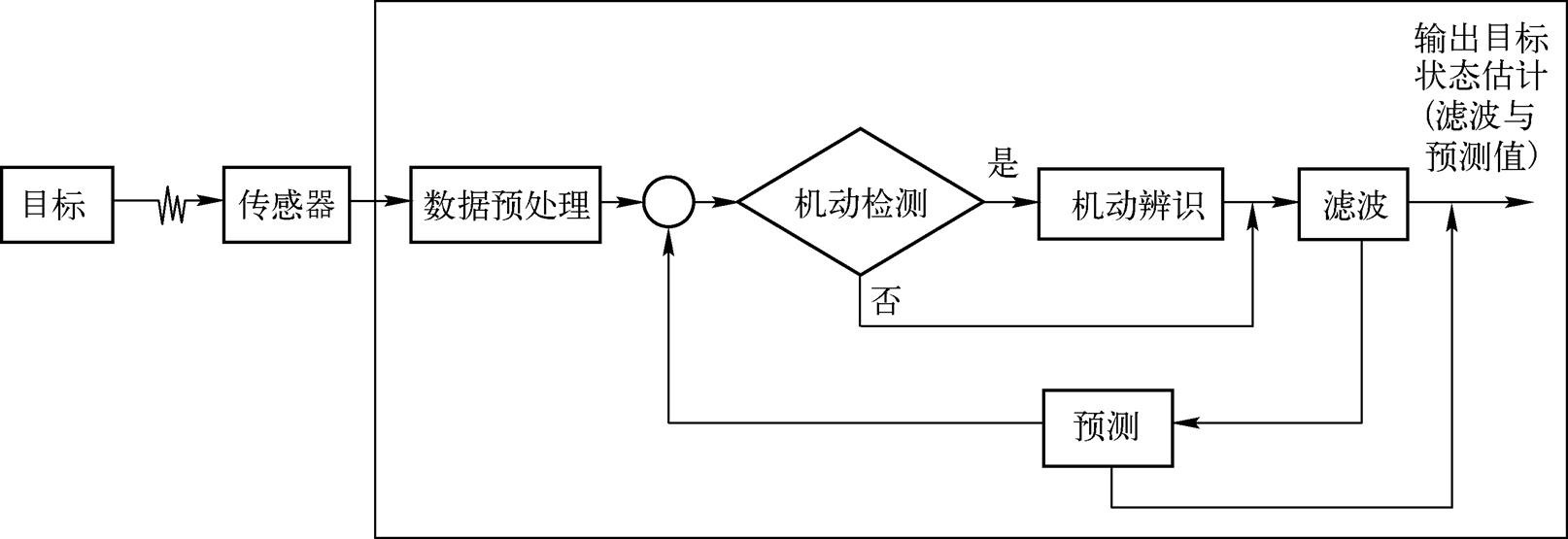
图1.2 单目标跟踪处理示意图
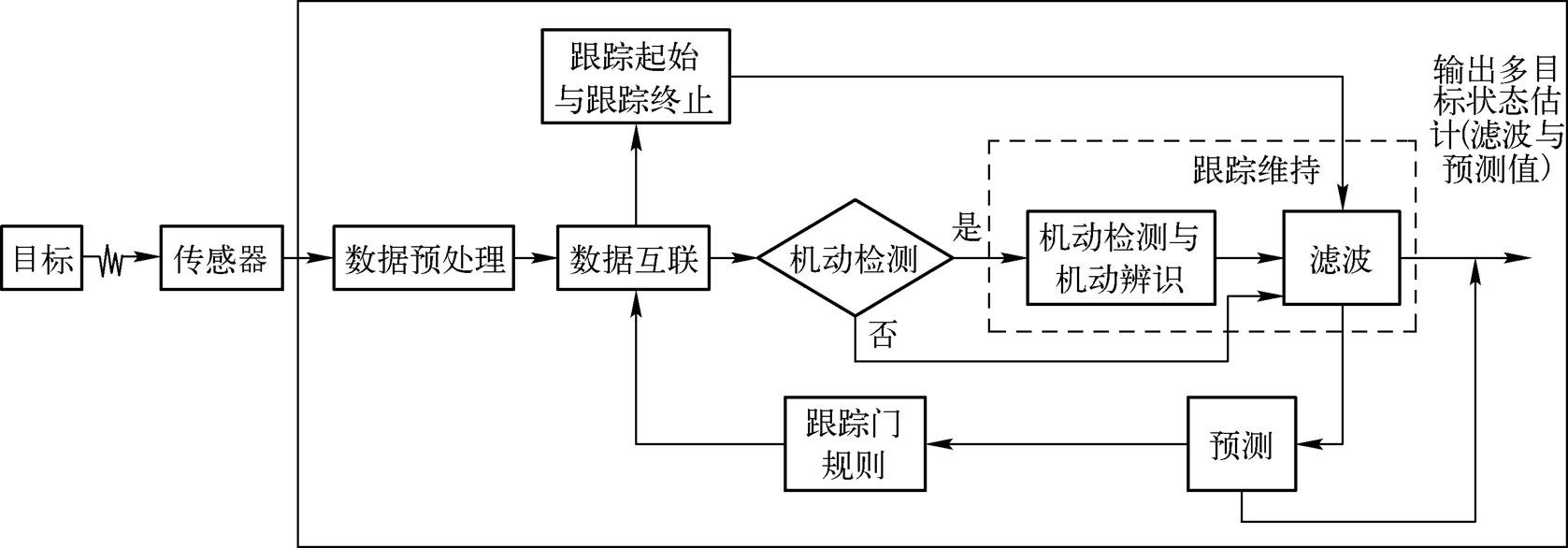
图1.3 多目标跟踪处理示意图
在以上单、多目标跟踪数据处理中，滤波和预测都是不可获取的核心处理环节，其主要目的是从观测数据中滤掉随机干扰（噪声），估计当前和未来时刻目标的运动状态，包括位置、速度和加速度等。例如，把观测到的目标坐标位置中的随机误差尽可能降低，把比较“平滑”的坐标变化情况显示出来，并根据目标坐标的变化规律确定目标运动参数。这就是火控系统求解计算射击诸元之前首先需要解决的重要问题。
跟踪处理机输入的目标不同时刻坐标是由雷达、声呐或光学仪器等传感器测得的，测量过程中不可避免地会带来“随机误差”。随机误差的特点是相对实际准确值呈正负快速变化，且与目标运动引起的坐标变化相比是很快的。图1.4为坐标 X 分量的情况。对 X 分量微分后，可得 X 分量的速度；对速度微分后可得相应的加速度。在用微分求取目标运动参数时，由于随机误差是快变化信号，其变化率很大。因此，经过微分后会给求得的目标运动参数带来很大的误差，甚至可能达到严重歪曲的地步。因此，在求取目标运动参数时要设法“滤”去随机误差。引入滤波计算就是要减小这种随机误差对求取目标运动参数的影响，而保留目标运动引起的真实坐标变化值（称为有用信号）。所以在求取目标运动参数时滤波是必不可少的。
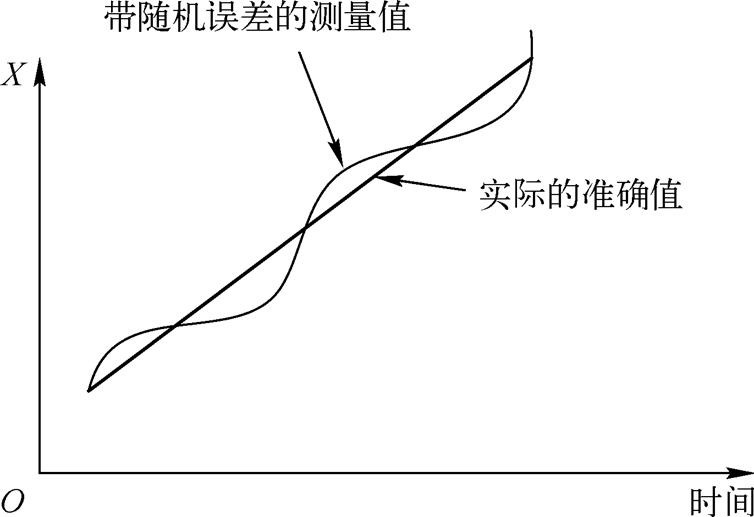
图1.4 X 分量
在滤波问题里，所依据的观测数据是有限的。根据这些观测数据，不可能完全消除随机误差，一般只能依据一定的准则来估计目标的运动状态，一般称为状态的最优估计。根据所估计目标状态对应的时间点，该最优估计可分为平滑、滤波和预测估计，如图1.5所示。
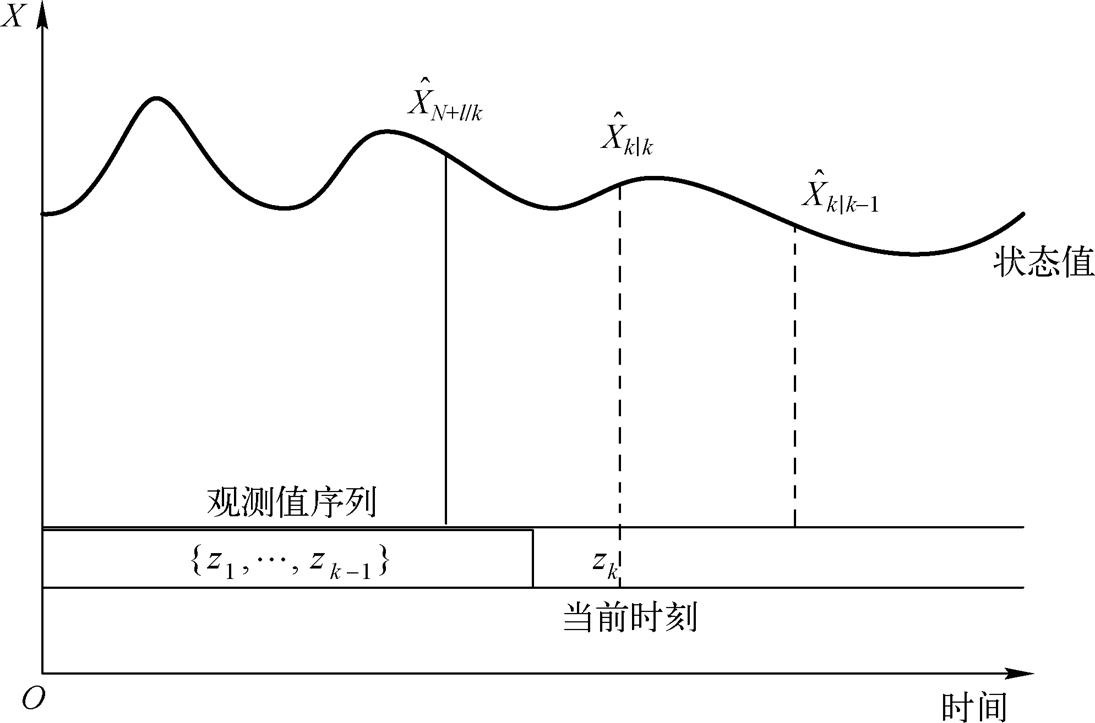
图1.5 平滑、滤波和预测关系示意图
（1）滤波。根据过去的所有测量数据
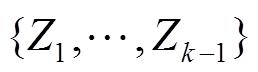，包括当前时刻
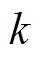的测量值
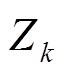，估计出当前时刻
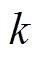的状态值
。
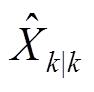（2）预测。根据过去的所有测量数据
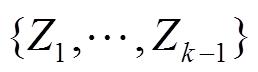，包括当前时刻
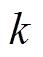的测量值
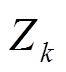，估计出未来时刻
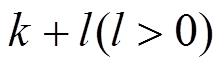的状态值
。
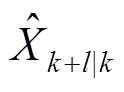（3）平滑。根据所有或一段测量数据
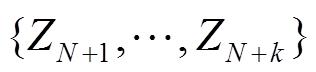，估计出过去某一时刻
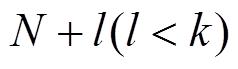的状态值
。
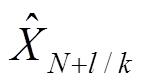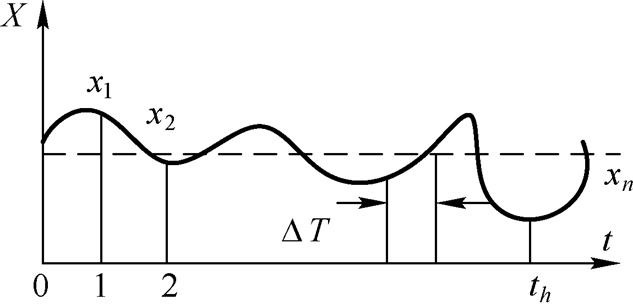
图1.6 算术平均法滤波示意图
为了理解滤波计算的原理，下面以算术平均法为例加以说明。图1.6是
X
分量的一系列带有随机误差的输入量。在观测时间
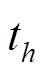内输入
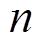个点，记为
,
,…,
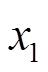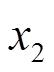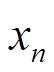。采样间隔为
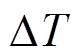，则第
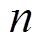点时刻的滤波值为：
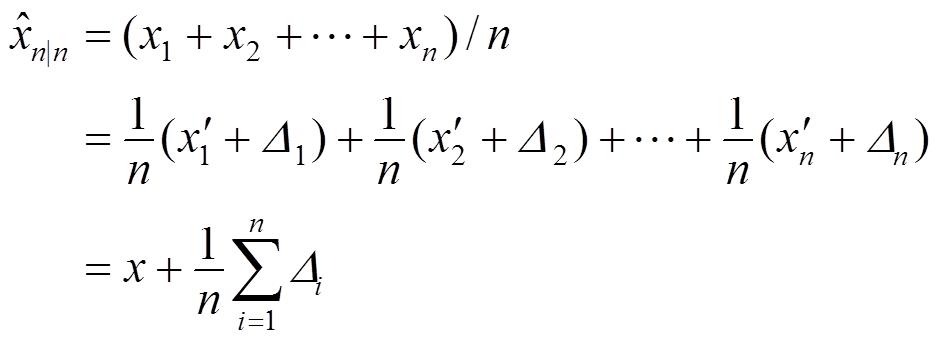
（1.2.1）
式中：
,
,…,
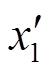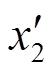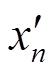为有用信号，这里假设它们都是相等的常数，且用
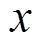表示。
,…,
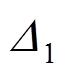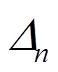为各采样点的随机误差。
经过如上处理后，显然能滤去部分随机误差。这种滤波的实质就是在所有输入采样中抽取相同的比例作为输出。在实际应用的滤波计算中，为了尽可能地“滤”去随机误差，保留有用信号，并能及时地反映输入的目标运动参数的变化。往往不采用简单的算术平均法，而是对不同的点采用不同的加权系数。
因此，围绕目标跟踪问题，在后续章节中将系统地介绍实现单目标跟踪、多目标跟踪的理论及其应用情况。下面介绍目标跟踪问题的研究历史和发展概况，这对我们深入理解该问题的复杂性是非常有帮助的。