





如何将点迹融合航迹关联的不确定信息用假设树描述出来,将信息相关性的度量引入算法中,建立假设树的结构模型,是实现点迹融合航迹关联的首要问题。点迹融合航迹关联是一个组合优化问题,其计算量随目标数量指数增加,因此必须寻求一种好的假设树构建方式,避免过多无效假设,从源头上减小总的计算量。
构建假设树的基本原理是根据当前被关联的点迹与融合中心航迹库的航迹初步关联的结果,按照关联的时间顺序和对应关系,对每一种关联可能建立一个多假设序列。假设树的构建过程如图2.18所示。在假设树的构建过程中,生成关联假设的可行性条件如下:
(1)每个点迹或融合航迹只属于1个目标,每个目标只有1个点迹或融合航迹来自同一信息源;
(2)每个信息源输出的目标个数不必相同,即使存在漏检和虚警的情况,每个目标至少有1个点迹或融合航迹;
(3)同一个信息源的点迹或融合航迹不能关联,而且来自1个信息源的1个点迹或融合航迹只能和另外1个信息源的1个点迹或融合航迹进行关联;
(4)时间和空间已经统一到1个基准点。
目标点迹或融合航迹信息通常来自不同平台不同信息源,每个信息源对应多个点迹或融合航迹。为描述方便,我们这里定义所有平台的信息源统一编号,各信息源编号唯一,即根据信息源ID就可以找到其对应的目标点迹或融合航迹。
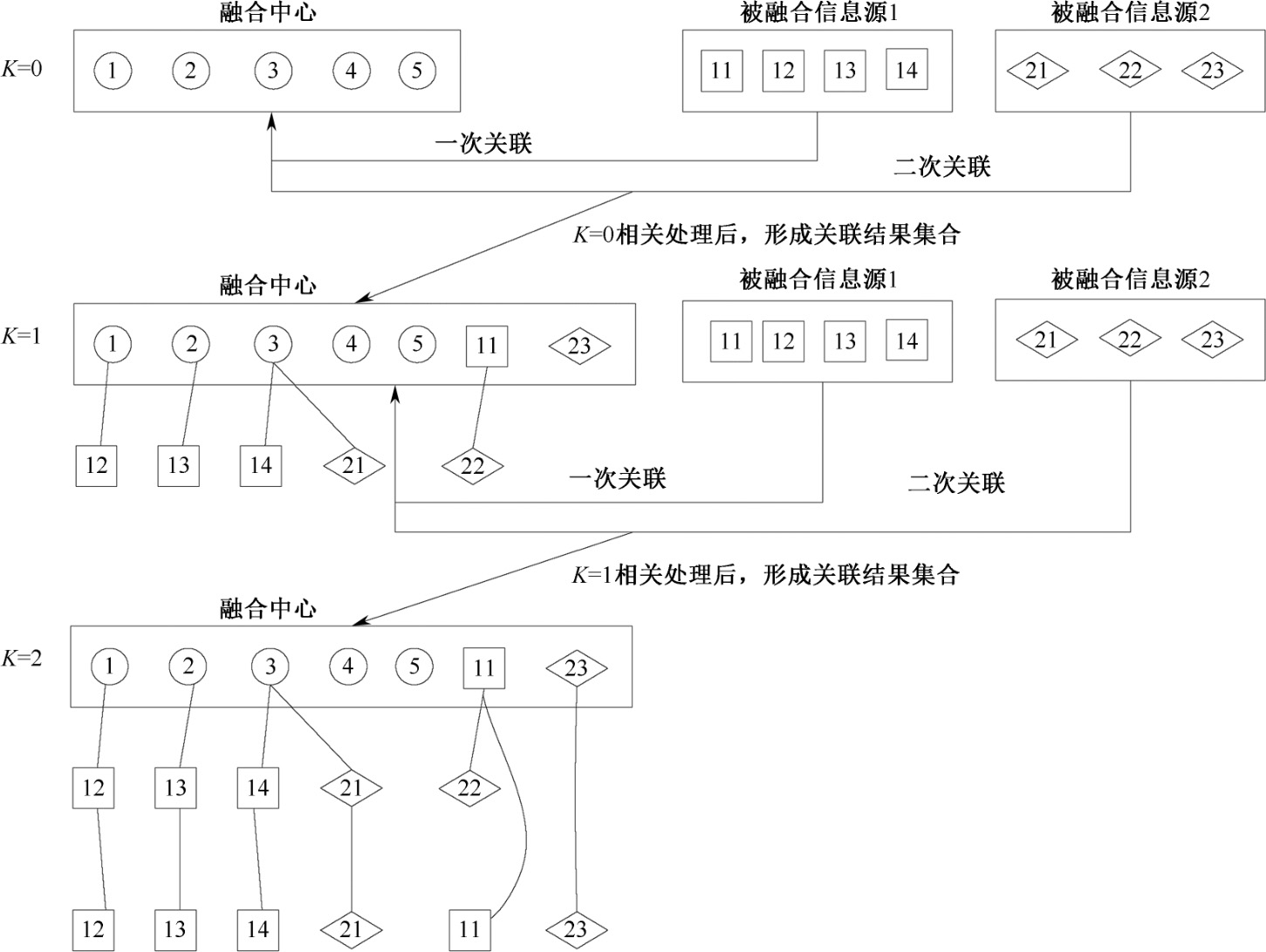
图2.18 假设树的构建过程
假设树作为一棵树,树的根节点是整个数据集合空间,每个节点对应一个关联假设,每个叶节点是属于单一类别的记录,其结构模型如图2.19所示。假设树的深度为4,第0层为根节点;第1层节点表示融合中心航迹库,包括初始航迹和新航迹,目标的ID唯一,信息源编号唯一;第2层每个节点表示被关联目标与融合中心的一种关联假设,同一层的节点之间的信息源编号和目标号可能重复,但每个时刻该层各个节点的信息源编号唯一;第3层节点是叶子,对应第2层每个节点在本层都有几个分支,即叶子,属于同一父节点的叶子,其信息源编号和目标批号相同,而时刻不同,叶子个数对应关联成功次数。
关联假设的形成过程为点迹融合航迹粗精两级关联,粗相关可以较大幅度地减少后续处理的计算量。在融合中心,根据点迹与融合航迹相似度判断是否能够关联,如果点迹与融合航迹的统计距离小于一个关联门限,那么它们可能来自同一个目标,这样的点迹与融合航迹称为一组关联假设。通常情况下,一个点迹或融合航迹可能不包含于任一关联假设,也有可能和另一传感器的多条点迹或融合航迹形成几组关联假设。
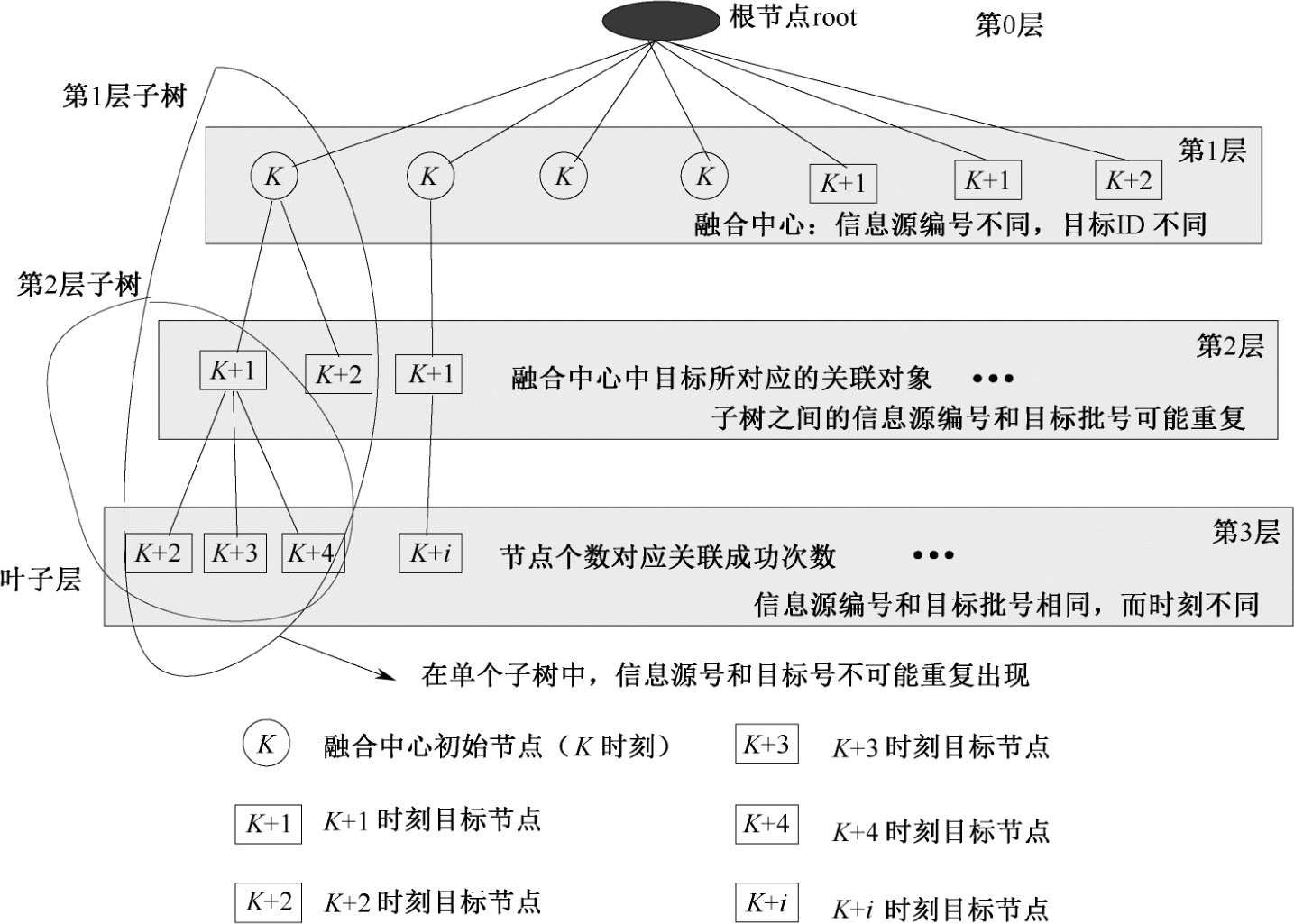
图2.19 假设树的结构模型
经过点迹融合航迹粗关联后,根据点迹融合航迹的相似性度量构建关联矩阵,其中相似性度量用关联系数 α ij 表示。形成关联系数的方法有加权法、修正法、序贯法、最近邻法和 K 近邻域法等,这里采用全局最近邻关联算法,其基本思想是,使统计距离总和最小的那些点迹融合航迹对为关联对。
为了描述问题的方便,假设送至融合中心的所有状态估计都经过时空对准。令来自节点1的点迹 i 和来自节点2的融合航迹 j 在 k 时刻的状态估计之差为
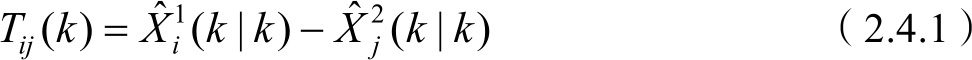
定义点迹 i ,融合航迹 j 在 k 时刻的统计距离为
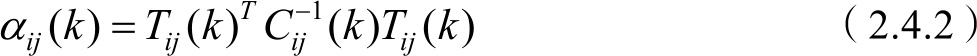
其中,
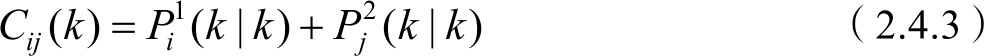
式中:
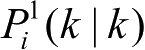 、
、
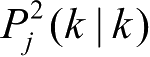 分别为点迹
i
、融合航迹
j
的估计误差协方差。
分别为点迹
i
、融合航迹
j
的估计误差协方差。
对来自节点1的 n 1 个点迹和来自节点2的 n 2 条融合航迹,计算两两间的统计距离便可得到关联矩阵
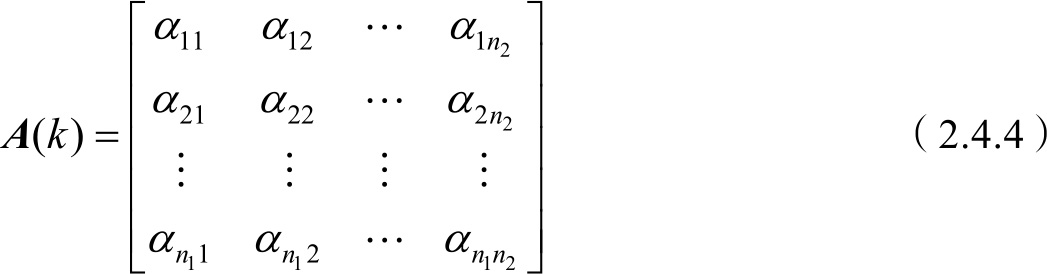
对该矩阵进行最优分配,便可得到 k 时刻的可能点迹融合航迹关联对,分配原则为:
(1)矩阵的每一行最多只有一个元素被分配;
(2)矩阵的每一列最多只有一个元素被分配;
(3)所有被分配元素的值总和最小。
则两局部节点下的点迹融合航迹关联问题为
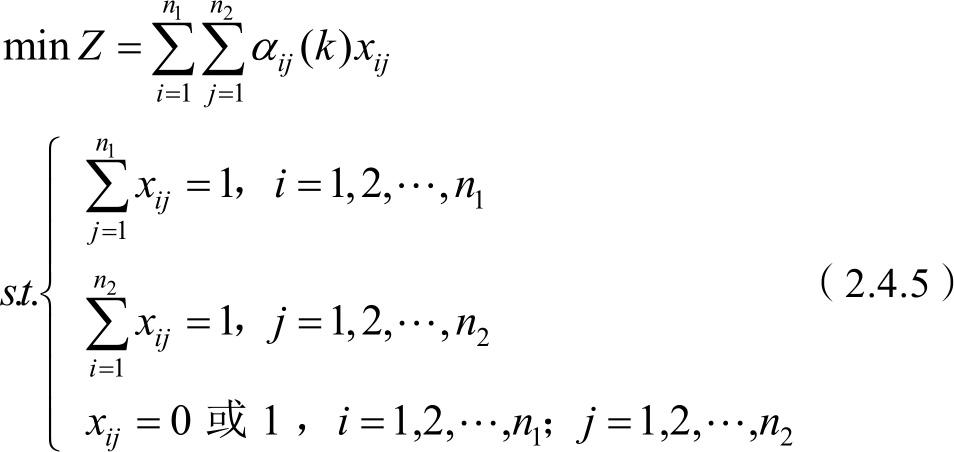
式中: x ij =1表明节点1的点迹 i 和节点2的融合航迹 j 关联; x ij =0表示不关联。
对于多局部节点下的点迹融合航迹关联问题,采用顺序处理结构,将来自各传感器的点迹融合航迹依次进行关联,两两进行关联检验和关联多义性处理。
构建关联假设树的前提是生成最佳关联假设,关联假设质量的好与坏直接影响假设树管理过程中的最优决策。工程实践中多传感器点迹融合航迹关联问题经建立适当的数学模型亦可转化为分配问题求解,而匈牙利算法是求解分配问题的一个非常有效的方法,它可以求出问题的精确解。根据点迹、融合航迹之间的全局最近邻相似度建立关联矩阵,将点迹融合航迹关联问题转化为分配问题,运用匈牙利算法求取该问题的最优解,从而生成最佳关联假设。