





相关波门是指以被跟踪目标的预测位置为中心,用来确定目标的观测值可能出现范围的一块区域。区域的大小由正确接受回波的概率来确定,也就是在确定波门的形状和大小时,应使真实量测以很高的概率落入波门内,同时又要使波门内的无关点迹不是很多。几种常见的相关波门包括直角坐标系下的椭圆(球)波门、矩形波门和极坐标系下的扇形波门。
目标直角坐标系下的量测值 z ( k +1)满足
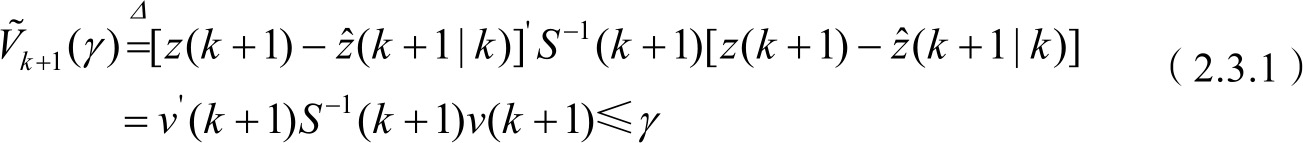
则称量测值
z
(
k
+1)为候选回波,式(2.3.1)称为椭圆(球)波门规则。其中参数
γ
由
χ
2
分布表获得;
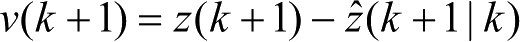 ;
S
(
k
+1)=
H
(
k
+1)
P
(
k
+1|
k
)
H
'(
k
+1)+
R
(
k
+1),
H
(
k
+1)为观测矩阵,
R
(
k
+1)为观测误差,
P
(
k
+1|
k
)为协方差的一步预测。若量测值
z
(
k
+1)为
n
z
维,则
;
S
(
k
+1)=
H
(
k
+1)
P
(
k
+1|
k
)
H
'(
k
+1)+
R
(
k
+1),
H
(
k
+1)为观测矩阵,
R
(
k
+1)为观测误差,
P
(
k
+1|
k
)为协方差的一步预测。若量测值
z
(
k
+1)为
n
z
维,则
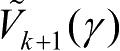 是具有
n
z
个自由度的
χ
2
分布随机变量。参数的平方根
是具有
n
z
个自由度的
χ
2
分布随机变量。参数的平方根
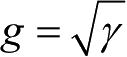 称为门的“
σ
数”。当
n
z
=2时,椭圆相关波门的形状如图2.2所示。
称为门的“
σ
数”。当
n
z
=2时,椭圆相关波门的形状如图2.2所示。
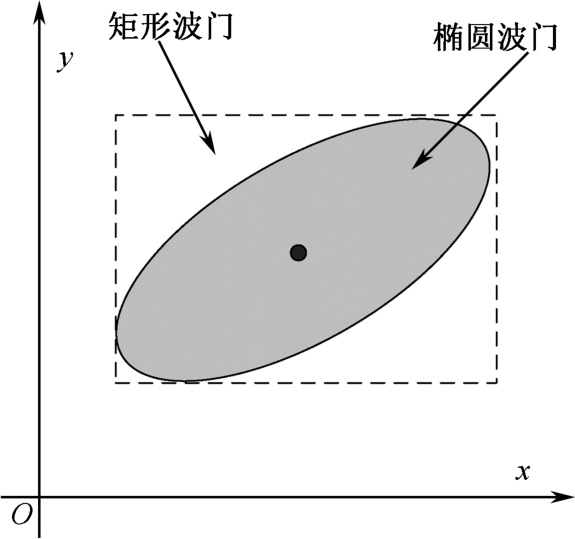
图2.2 椭圆相关波门的形状
对于不同
γ
值和不同量测维数
n
z
,真实量测落入波门内的概率
P
G
就不同,定义
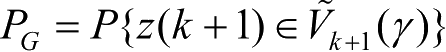 。
。
最简单的相关波门形成方法是在跟踪空间内定义一个矩形区域,即矩形波门。设新息
v
(
k
+1)、量测
z
(
k
+1)和量测的预测值
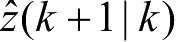 的第
i
个分量分别用
v
i
(
k
+1)、
z
i
(
k
+1)和
的第
i
个分量分别用
v
i
(
k
+1)、
z
i
(
k
+1)和
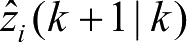 表示,新息协方差
S
(
k
+1)的第
i
行第
j
列的元素用
S
ij
表示,则当量测
z
(
k
+1)的所有分量均满足关系
表示,新息协方差
S
(
k
+1)的第
i
行第
j
列的元素用
S
ij
表示,则当量测
z
(
k
+1)的所有分量均满足关系
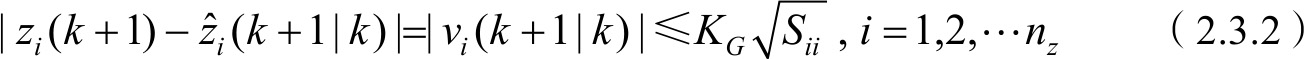
则称量测 z ( k +1)落入矩形波门内,该量测为候选回波。其中, K G 为波门常数,在实际应用中往往取较大的 K G 值( K G ≥3.5)。
若相关是在量测坐标系(极坐标系)下进行的,传感器测得的目标量测值 ρ 、 θ 满足
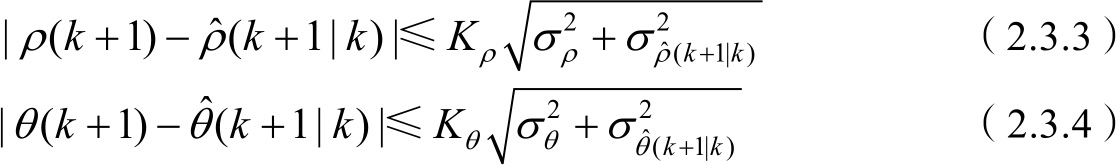
则称量测
ρ
、
θ
落入扇形波门内,该量测为候选回波。其中,
K
ρ
、
K
θ
为由
χ
2
分布表查得的参数的平方根;
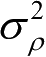 和
和
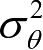 分别为极坐标量测值
ρ
和
θ
的量测误差方差;
分别为极坐标量测值
ρ
和
θ
的量测误差方差;
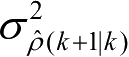 和
和
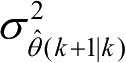 分别为对应的预测值的方差。扇形波门的形状如图2.3所示,其尺寸大小与
χ
2
分布表查得的参数、
分别为对应的预测值的方差。扇形波门的形状如图2.3所示,其尺寸大小与
χ
2
分布表查得的参数、
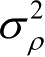 、
、
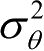 及
及
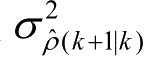 、
、
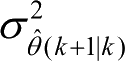 有关。
有关。