





基于航迹的MHT算法在每次扫描完成后用已更新的航迹重新计算了假设,并不是保存和扩展。从一次扫描到下一次扫描过程中,面向航迹的方法丢弃了 k -1次扫描时的假设,从修剪中幸存下来的航迹被用来预测下一次即第 k 次扫描中的航迹。在第 k 次扫描中,应用已更新的新航迹形成新的假设。除了根据小概率或者N-scan修剪规则删除一些航迹外,没有任何信息丢失,这是因为包含了所有相关统计数据的航迹评分被保存了下来。
MHT的流程可以大体分为两个步骤:数据关联以及航迹维护,如图2.1所示。数据关联是将读入的扫描数据按照其所处的波门和已有的航迹进行关联,要求把所有落在波门内的扫描数据和相应的航迹都关联起来,暂时不考虑航迹的质量。需要注意,某个数据和其对应的航迹关联起来,并不等于说该数据就是这个航迹中目标的新观测数据,该数据可能是虚警,该数据也可能是一个新目标的起始,这些问题的最终确定需要等到航迹维护时进行。这反映了MHT的基本思想:把困难的数据关联操作推后,等到获取更多的观测数据后再进行。如果扫描数据没有落在任何一个波门内,则该数据直接产生一个新的航迹。另外,如果在航迹的波门内没有观测数据,则利用预测技术将航迹外推,并形成新的波门。
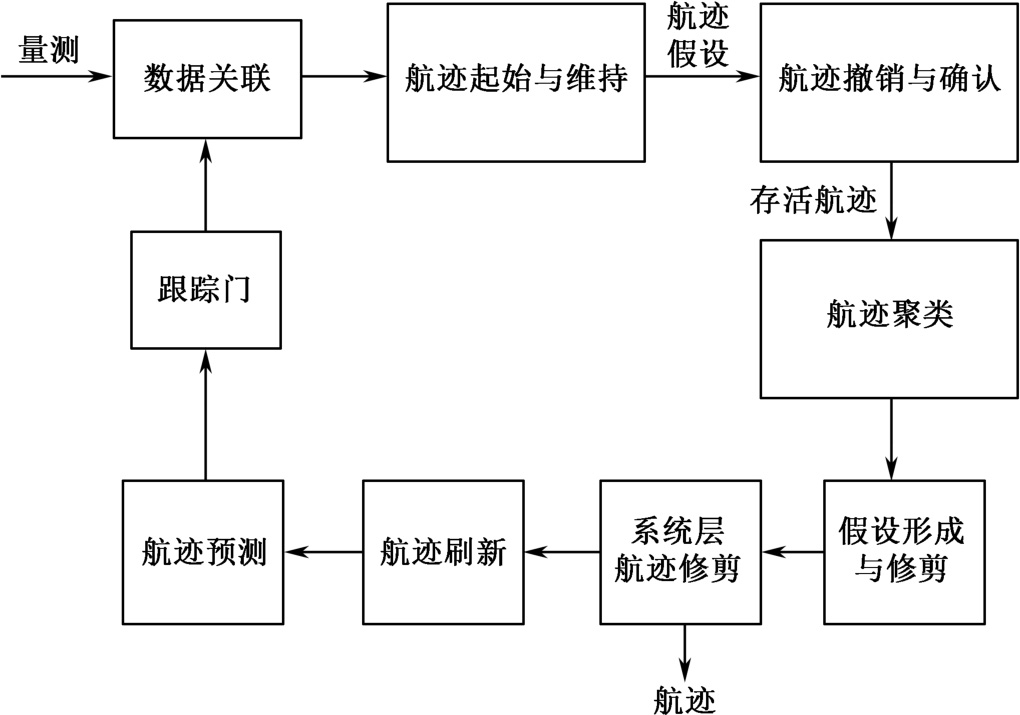
图2.1 基于航迹的MHT流程
算法主要步骤如下:
目标点迹与航迹数据关联可能是通过计算可能目标状态值与预测的目标状态值之间的归一化距离 d 2 来进行的。
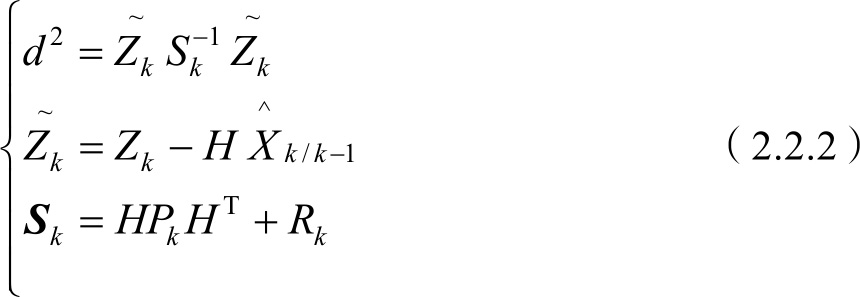
式中:
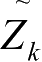 为量测值与预测值之间的矢量差(残余矢量);
S
k
为量测过程的残余协方差矩阵。
为量测值与预测值之间的矢量差(残余矢量);
S
k
为量测过程的残余协方差矩阵。
由上式,我们可以计算出每一个新的量测数据与相应航迹的预测值距离。当距离小于关联门限时,我们就可以将此量测数据与相应航迹进行关联。
航迹置信度由递归积累产生,每个航迹的置信度等于它上一次的值加上一个置信度增量Δ L k ,即初始值为

式中: P d 是目标探测的几率; P f 是虚警概率; d 是目标航迹预测值与量测值之间的距离; β F 是虚警空间探测密度; M 是量测空间维数; S 是量测过程的残差协方差矩阵。
由上面的公式给出的航迹置信度就可以用来进行序列概率比测试,测试的数据如下: L k ≤ T L ,删除航迹; L k ≥ T U ,确认航迹; T L < L k < T U ,等待更多的数据更新航迹。 T L 为定义的航迹删除域值, T U 为航迹确认域值。
航迹聚类的过程就是将与公共量测相关联的所有航迹收集到一起。共享量测的航迹被定义为不相容的航迹。航迹聚类除了包括共享量测的航迹(直接共享),还包括那些与第三条航迹共享量测的航迹(间接共享)。因此,若航迹1与航迹2共享一个量测,航迹2与航迹3共享一个量测,则所有的航迹都在同一个航迹聚类中。需要注意的是,算法要根据航迹的新增或删除进行聚类的合并或分割。
假设形成的目的是为了考虑冲突航迹的相互影响,获得一致的关联结果,分别在不同的航迹群内完成,相互兼容的候选航迹集合可形成一个假设。一个从航迹聚类中产生的完全假设由以下步骤生成:
(1)开始假设集合为空;
(2)从一个航迹群的航迹列表中任意选取一条航迹;
(3)从剩下的航迹列表中找出所有与被选出航迹相兼容的航迹;
(4)把挑选出来的航迹组成一个航迹列表,重复步骤(3)、(4),直到剩余的航迹都与新航迹列表中的航迹冲突;
(5)从初始航迹列表中去掉第一条被选出的航迹,重复步骤(2)~(4),直到得到所有的假设。
假设构造过程中,我们就可以完成对假设的置信度计算,假设的置信度等于构成这个假设的所有航迹的置信度之和。我们只保留置信度最高的几个假设。那些被删除的假设中包含的航迹也被删除。通过这次基于假设的航迹删减,航迹的数目大大减少。最后一个步骤,所有幸存的航迹通过Kalman滤波器来更新它的状态,并预测下一次扫描的状态。
MHT算法中用Kalman滤波器来进行航迹的更新和预测,离散Kalman滤波器的目标状态方程和观测方程为
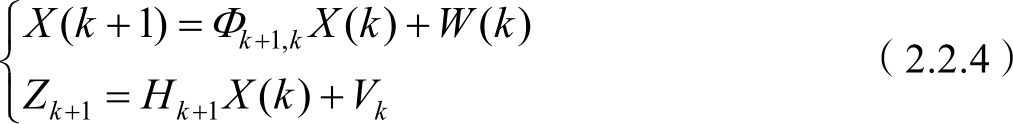
Kalman滤波器中目标的模型是单一的,如果目标发生机动,其对目标状态的预测偏离目标的真实状态,导致算法第一步中数据关联的归一化距离 d 2 增大,严重影响数据关联的正确率;在算法的第二步航迹的确认与删除中, d 2 的增大使得航迹的置信度减少,正确的航迹有可能会被删除,导致航迹起始失败。