




复合材料的非线性力学行为很早就引起了科研人员的广泛关注,他们研究了由高分子树脂基体的粘弹性行为 [16-20] 、偏轴加载 [21-25] 及纤维编织形式 [26-30] 等引起的非线性力学行为,并结合物理机理建立本构关系,提出了不同的复合材料非线性力学行为预测模型 [31-42] 。
对于传统纤维增强复合材料,可将纤维看作是线弹性的,而聚合物基体则表现出非线性(在高温下更明显)。在纤维断裂和基体开裂以前,由受力分析可知,复合材料在纤维横向和面内剪切的非线性力学行为主要是由于软化型聚合物基体的非线性引起的,而基体材料的非线性对纤维方向模量和泊松比的影响可以忽略。
传统纤维增强复合材料偏轴拉伸时有较明显的非线性,尤其是45°方向偏轴拉伸的非线性最明显。复合材料中的纤维在未与树脂基体复合前是柔软的,只能承受轴向应力。当载荷不沿复合材料的纤维方向时,由于复合材料是一个结构,应力按纤维和树脂基体的结构来分配,纤维和树脂基体都处于复杂应力状态,特别是树脂基体,此时树脂基体除承受拉伸应力外,还要承受剪切应力。
而对于纤维编织形式引起的非线性,由于材料增强体为三维空间网状连续纤维结构,其细观结构极为复杂,需要分析增强织物的取向、组织结构、线圈形态、几何与结构参数等因素,直接建立材料力学性能预报模型困难很大,许多科研人员通常基于周期性单胞来研究材料的基本力学行为。
总结上述研究结果 [43] ,传统纤维增强复合材料由偏轴拉伸和剪切引起的非线性尤为明显,主要原因有:①基体的非线性(此时,正轴拉伸时也存在基体非线性,但常被忽略);②纤维的转动;③基体逐步开裂。
在一般情况下,传统纤维增强复合材料的非线性力学行为按照基体的种类分为两种情况 [44-66] :①纤维增强热固性树脂基体复合材料,主要表现在偏轴拉压和剪切应力—应变的非线性,垂直于纤维的复合材料横向表现出较弱的非线性,而方向性拉压表现出较明显的非线性;②纤维增强热塑性基体复合材料,除了热固性基体复合材料的情况,还要考虑基体对非线性的影响。
研究纤维增强复合材料非线性本构关系的方法可分为宏观力学法和细观力学法,大多数科研人员采用宏观力学法。宏观力学法把复合材料看作均匀的非线性各向异性材料,因此,必须在各材料主方向上建立不同的非线性本构关系 [2] 。
对于复合材料非线性的研究,目前更多的是偏向于偏轴引起的非线性研究,对于由基体粘弹性引起的非线性主要集中在对热塑性基体复合材料的研究上。由于本书研究的复合材料采用的是热固性基体,不具备粘弹性性能,所以对于基体粘弹性引起的非线性本书不再赘述。
1.第一类方法——增量法
Petit和Waddoups在20世纪60年代提出基本数据组结点之间用分段线性插值函数表示单向层合板的非线性力学行为。在这种方法中,硼/环氧复合材料层合板在材料主方向上承受拉伸载荷、压缩载荷和剪切载荷。用这种概念与简单层合板理论相结合,来确定层合板承受增量施加的面内载荷时的响应。在每个增量中,假设材料性质保持不变和独立,而且应力或应变可以从前一次增量中得到。Petit和Waddoups运用线性单层板和层合板本构关系,并且使用分段线性的应力—应变曲线表达增量地施加平均层合板应力
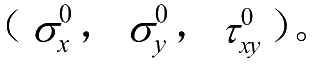 即对层合板施加平均层合板应力的增量
即对层合板施加平均层合板应力的增量
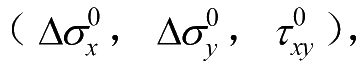 并用初始层合板柔度矩阵[
s
]
T
,假设层合板对于施加的应力增量表现为线性,可计算层合板应变的第一次增量:
并用初始层合板柔度矩阵[
s
]
T
,假设层合板对于施加的应力增量表现为线性,可计算层合板应变的第一次增量:
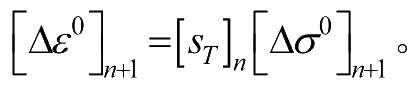 其中,
n
表示第
n
次值。然后,把层合板应变的增量
其中,
n
表示第
n
次值。然后,把层合板应变的增量
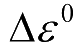 加到先前的应变上,以确定当前总层合板应变:
加到先前的应变上,以确定当前总层合板应变:
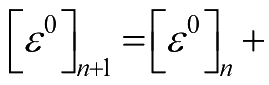
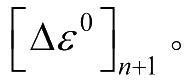 随着载荷增量的进行,可记录单独的单层板应变,并通过参考单层板试验应力—应变曲线,把
E
1
,
E
2
,
G
12
视为第
n
次单层板应变值的切线模量,由此可计算出相应的单层板在当前应力水平下的切线模量或刚度。这种方法通过单层板应变的第
n
次值得到第(
n
+1)次载荷增量的层合板柔度矩阵,显然层合板的应力—应变曲线在很大程度上取决于产生累积误差的载荷增量的大小。
随着载荷增量的进行,可记录单独的单层板应变,并通过参考单层板试验应力—应变曲线,把
E
1
,
E
2
,
G
12
视为第
n
次单层板应变值的切线模量,由此可计算出相应的单层板在当前应力水平下的切线模量或刚度。这种方法通过单层板应变的第
n
次值得到第(
n
+1)次载荷增量的层合板柔度矩阵,显然层合板的应力—应变曲线在很大程度上取决于产生累积误差的载荷增量的大小。
Hashin-Bagchi-Rosen用碳纤维增强树脂复合材料单层板横向应变和剪切应变曲线的Ramberg-Osgood公式(一个描述材料在其屈服点附近应力—应变关的系理论模型)和变形理论描述层合板非线性力学行为。在分析单层板应变ε时,将其分解为弹性应变 ε ′和非弹性应变 ε ′,非弹性应变 ε ′用Ramberg-Osgood公式的形式给出。层合板分析相当复杂,对于 n 层层合板,可写出有关3 n 个应力的3 n 个方程,这些方程可用迭代法进行数值求解。
Sandhu用分段三次插值函数来逼近基本性质数据集,表示出了全部非线性应力—应变关系(拉伸、压缩和剪切)。在这种理论中,基于获得的试验数据(对硼/环氧增强树脂复合材料进行偏轴拉伸试验),假设单层板中的法向应变是由法向应力引起的,而剪切应变是由剪切应力引起的,这种理论与简单层合理论相结合,可预测层合板的力学行为。增量地施加面内载荷,对于每次施加的增量,用迭代法求得应变。Sandhu的这种方法可以解决Petit-Waddoups法过度依赖载荷增量大小的问题。首先,这种方法用分段三次插值函数来表示基本的应力—应变数据,然后,使用预测值—校正值和迭代法。这种方法用在第 n 次载荷增量之后的弹性性质得到的单层板应变来确定在相同载荷增量下的平均层合板柔度,并且得到一组新的层合板应变。重复这个程序直到连续两组层合板应变之间的差别小于一个规定值。这种方法使层合板应力—应变曲线对载荷增量大小的依赖减小。
Jones-Nelson-Morgan认为非线性力学性质是应变能密度的函数,即材料的力学性质可表示为
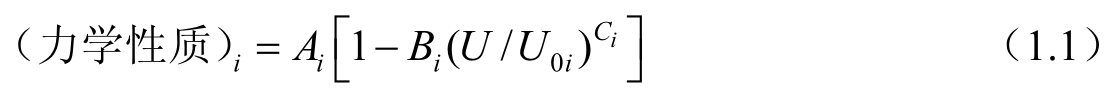
式中,
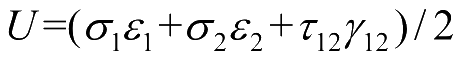 ;
A
i
、
B
i
和C
i
分别是应力—应变曲线初始斜率、初始曲率和第i次应力—应变曲线的曲率改变,它们由数据拟合确定,并用
U
0
来对力学性质方程中的应变能部分做无因次化。从式(1.1)中可以明显地看到,应变能是用特定点的割线模量进行计算的。这种方法说明,实际的最大应变能可以超过数据所定的极限,因为非线性分析是运用在多轴应力状态的,这时的应变能要比力学性质测量时单轴应力状态的应变能大。因此,应力—应变曲线和力学性质—应变能曲线要用一种相当复杂的方法进行外推,然后用迭代法得到应力—应变曲线。在每次非线性迭代过程中,对由前一次迭代的应变能确定性质的线弹性系统进行分析。对于层合板,迭代方法必须满足应力—应变关系、应力平衡和应变协调。尽管这种方法看起来较全面,但也很复杂。这种复杂性与Hahn-Tsai的结果比较时,并没有表明可获得更好的结果,其进行的试验为硼/环氧增强树脂复合材料的偏轴拉伸试验。
;
A
i
、
B
i
和C
i
分别是应力—应变曲线初始斜率、初始曲率和第i次应力—应变曲线的曲率改变,它们由数据拟合确定,并用
U
0
来对力学性质方程中的应变能部分做无因次化。从式(1.1)中可以明显地看到,应变能是用特定点的割线模量进行计算的。这种方法说明,实际的最大应变能可以超过数据所定的极限,因为非线性分析是运用在多轴应力状态的,这时的应变能要比力学性质测量时单轴应力状态的应变能大。因此,应力—应变曲线和力学性质—应变能曲线要用一种相当复杂的方法进行外推,然后用迭代法得到应力—应变曲线。在每次非线性迭代过程中,对由前一次迭代的应变能确定性质的线弹性系统进行分析。对于层合板,迭代方法必须满足应力—应变关系、应力平衡和应变协调。尽管这种方法看起来较全面,但也很复杂。这种复杂性与Hahn-Tsai的结果比较时,并没有表明可获得更好的结果,其进行的试验为硼/环氧增强树脂复合材料的偏轴拉伸试验。
Amijima-Adachi通过对纤维增强树脂基层合板的拉伸和压缩试验观察了复合材料的非线性应力—应变现象,尤其对φ±角铺设层合板的偏轴加载试验显示出了不同程度的非线性。尽管这种方法是在前几种方法出现之后给出的,但是从根本上说,这并不是一种新方法。它仅限于剪切非线性,非线性用许多直线段表示,即剪切应力—应变曲线被分为 n 个小段,在以下每个增量中认为是直线,该增量的表达式为

对于单向层合板和角铺设层合板来说,Δγ
12
与
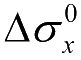 之间的方程较容易得到,然后可得到层合板应变增量,并预计层合板的非线性应力—应变关系。通过叠加各单向单层板或角铺设单层板来分析应力—应变响应。
之间的方程较容易得到,然后可得到层合板应变增量,并预计层合板的非线性应力—应变关系。通过叠加各单向单层板或角铺设单层板来分析应力—应变响应。
2.第二类方法——Hahn-Tsai法及其演变
1973年,Tsai和Hahn [16] 用应变余能密度研究了单向复合材料层合板平面剪切非线性力学行为的本构关系,并使用硼纤维增强环氧树脂复合材料板和碳纤维增强环氧树脂复合材料板进行试验,以证明结果的准确程度。他们将轴向与横向的应力—应变关系看成线性以简化计算模型,虽然没有得到普适性的结果,但是可以进行推广,并展示了如何在特定的载荷条件下得到相对准确的本构方程,最后还证明了使用应变能密度推导本构关系是不合适的。Hahn-Tsai用弹性应变余能密度推导出了一种应力—应变关系。这种方法忽略了面内法向应力和剪切应力之间的耦合。在应用时,他们仅考虑层合板非线性的主要贡献者——剪切非线性力学行为,并引入一个附加的四阶常数(大于0)来考虑剪切的非线性力学行为,即
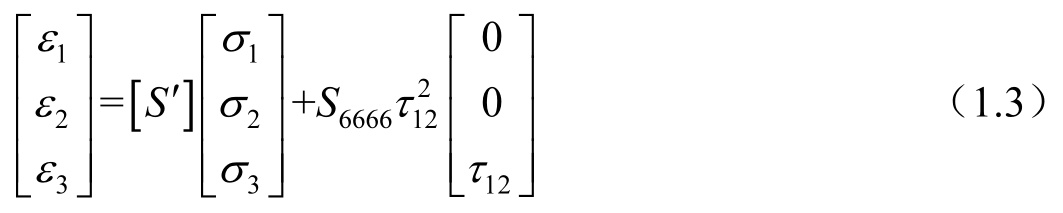
他们把上述研究单层板的方法推广到层合复合材料,采用的方法为常规方法,先把方程转换为 x - y 轴系统,然后利用层合理论得到层合板应力与应变之间的关系。每步都引入新的函数,这样的分析有些复杂,它只考虑了剪切响应的非线性,并且引入了一个新的常数S 6666 ,它必须由±45 °层合板的单向拉伸试验来确定。
夏源明等人 [17] 在Hahn-Tsai非线性弹性理论的基础上,导出了复合材料板在平面应力状态下的一般非线性本构关系;并使用单向拉伸(纵向和横向)和双向拉伸试验验证了单向复合材料板在纵向和横向应力之间不存在非线性耦合,从而获得了一个简化而又实用的本构关系,并通过试验,验证了推导所得本构方程与试验数据偏差在容许范围内,可以接受。试验所用材料是玻璃纤维增强环氧树脂复合材料,同时验证了以碳纤维或硼纤维作为增强材料的复合材料也有相似的结果。
该模型的一般的应力—应变关系可表示为
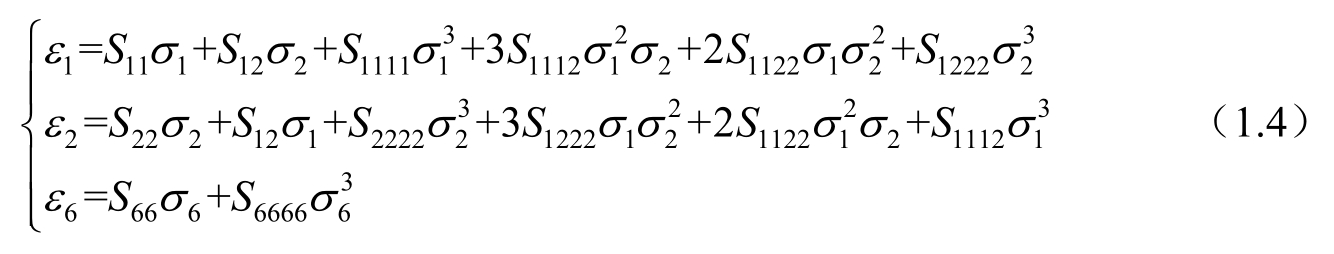
我们分别通过沿1、2方向的单向拉伸试验,1和2两方向的双向拉伸试验确定上述关系式中的各参数。经过简化后,得到本构关系式为
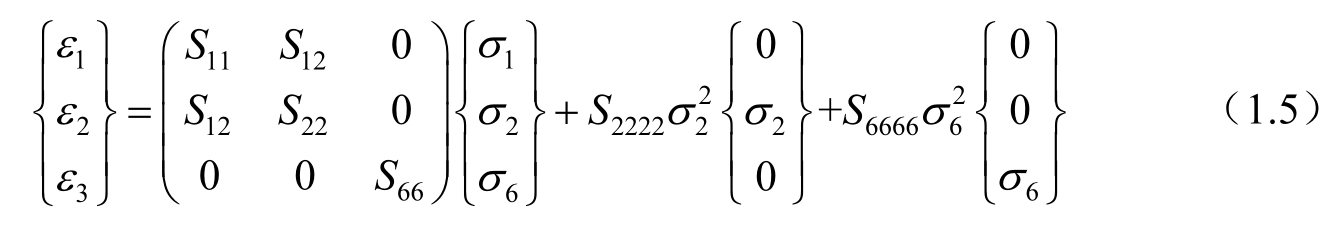
对于偏轴拉伸引起的非线性力学行为的分析,1989年Sun和Chen [18] 建立了描述基于纤维增强复合材料非线性力学行为本构模型的流动法则。这个适用于正交各向异性具有非线性的单参数流动法则可以用来描述纤维增强复合材料的非线性力学行为。考虑到大部分复合材料在轴向表现出很小的非线性,单参数足以胜任。利用有效应力与非线性应变增量,得出了一个普遍适用于正交各向异性复合材料的应力—应变本构关系,并经由硼增强的铝基复合材料和碳纤维增强的环氧复合材料试验证明该模型的准确性,得到非线性应变增量—应力之间的关系。
对于各向异性材料的非线性力学行为,Sun等人提出了一个带有单参数a 66 的流动准则,用以描述纤维复合材料表现出来的非线性。
该模型建立基于的屈服判据为
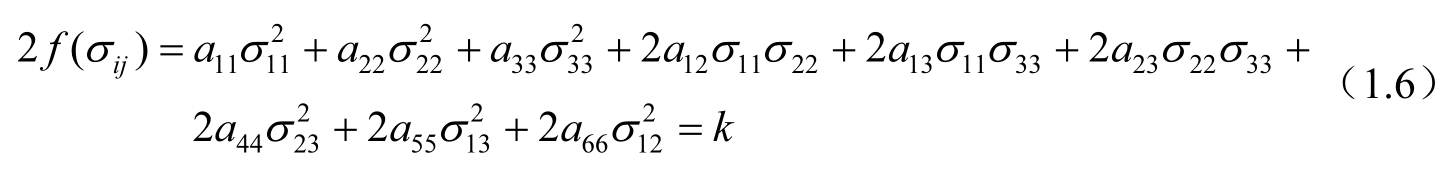
该屈服判据适用于各向异性材料,σ ij 为材料主方向上的应力,系数a ij 的值由试验确定,它描述了初始非线性力学行为的各向异性程度,当a ij 取值为式(1.7)所示时
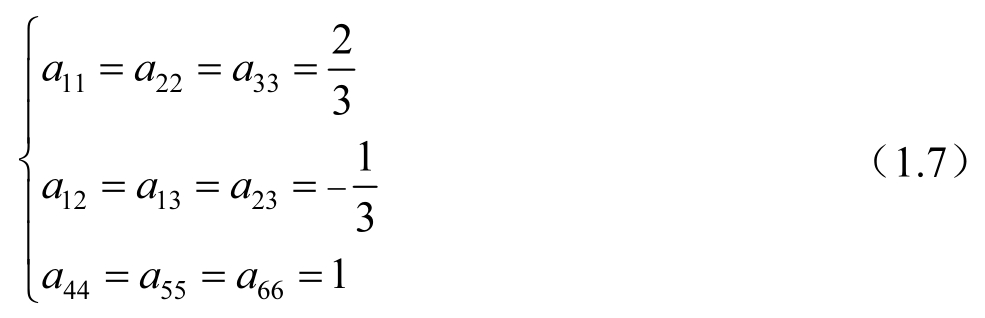
上面的判据就简化为Von Mises屈服判据。正交各向异性材料的Hill屈服判据是式(1.6)判据的一个特例,只要满足式(1.8)所示条件即可。
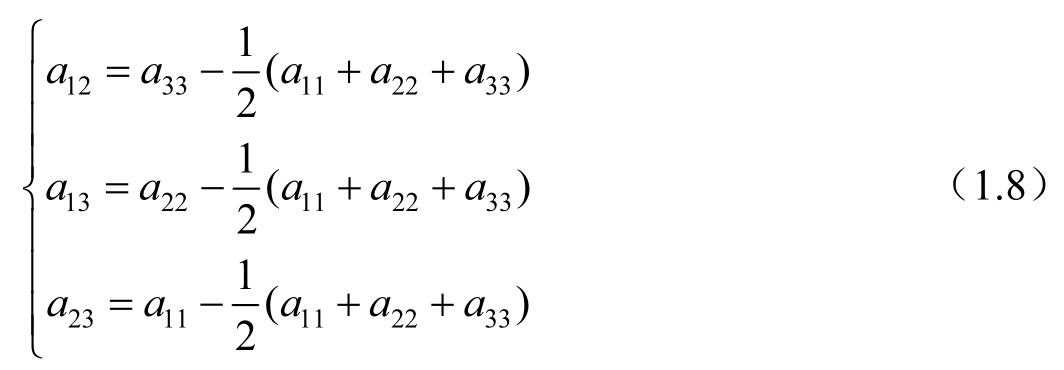
式(1.6)的屈服判据条件是复合材料塑性变形且具有不可压缩性,同时塑性变形与水静应力无关。根据相关的流变定律,屈服判据可取作塑性势能函数,从中可以导出式(1.9)所示的非线性应变增量,式(1.9)中上标 p 代表塑性,dλ是比例系数。

单位体积塑性功增量由式(1.10)给出,即

将其有效应力
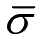 定义为
定义为

有效非线性应变增量
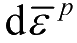 可以按式(1.12)定义,即
可以按式(1.12)定义,即

前人的大量试验结果表明,纤维复合材料在沿纤维方向受力时表现出线性特征(此时忽略植物纤维的加捻),因此可以假设

进而得到式(1.14),即

由此,塑性势能函数式(1.6)可简化为式(1.15),即

由式(1.15)可以导出非线性应变增量为
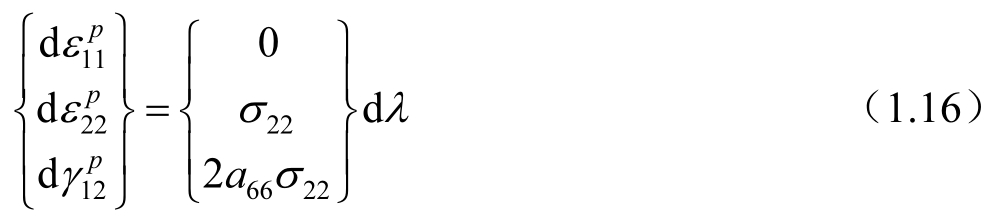
相应的有效应力为

同时,非线性应变增量简化为
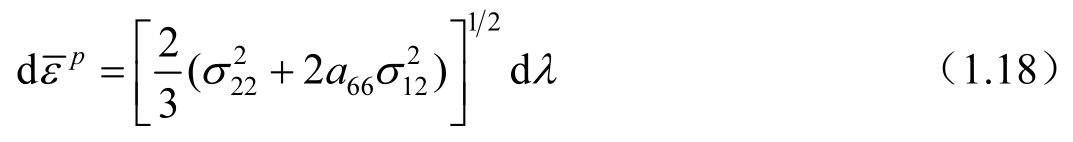
非线性应力—应变的增量关系完全由 a 66 和dλ决定,材料常数 a 66 可以由偏轴静力试验获得。
2009年,Yokozeki等人 [19] 建立了复合材料的弹塑性本构关系模型,该力学模型认为,复合材料的应变包括弹性变形和塑性变形两部分,即
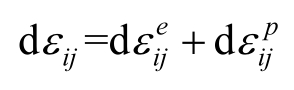
其中,弹性部分的经典变形公式为
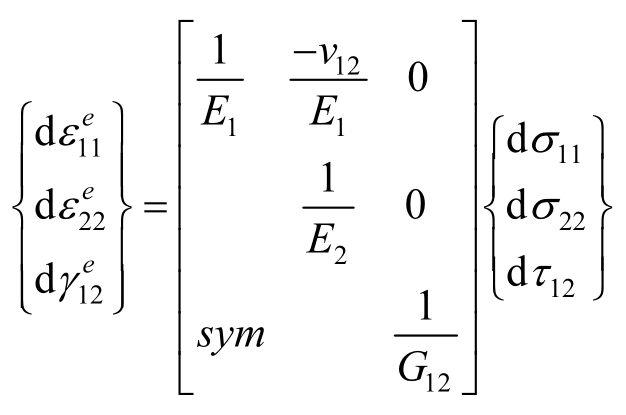
而塑性部分的变形,Yokozeki等人在Sun-Chen塑性模型的基础上引入了应力方向上的参数 a 1 ,得到有效应力为
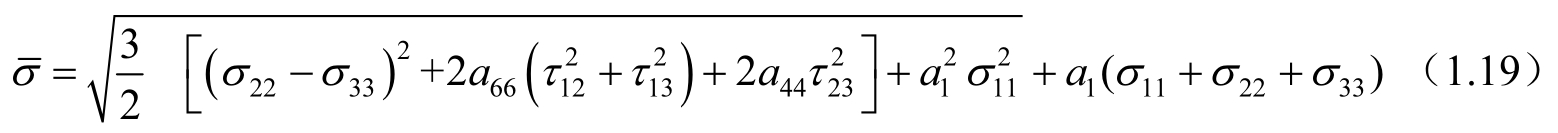
在1、2平面应力状态下的有效应力为
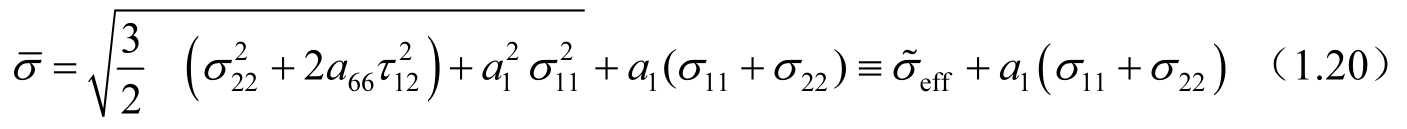
其假定在真应变范围以内,纤维方向的塑性变形可以忽略不计,且
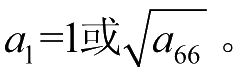
这样应变增量为
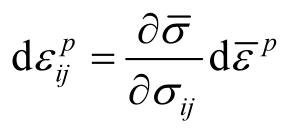
即
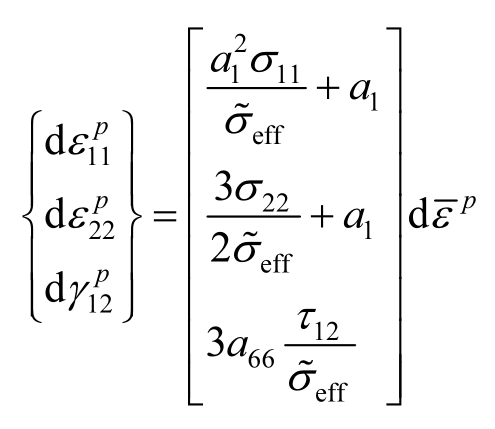
而根据Sun-Chen塑性模型的有效应变与有效应力间的关系
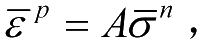 可以得到在平面应力状态下塑性部分的应力—应变公式,即
可以得到在平面应力状态下塑性部分的应力—应变公式,即
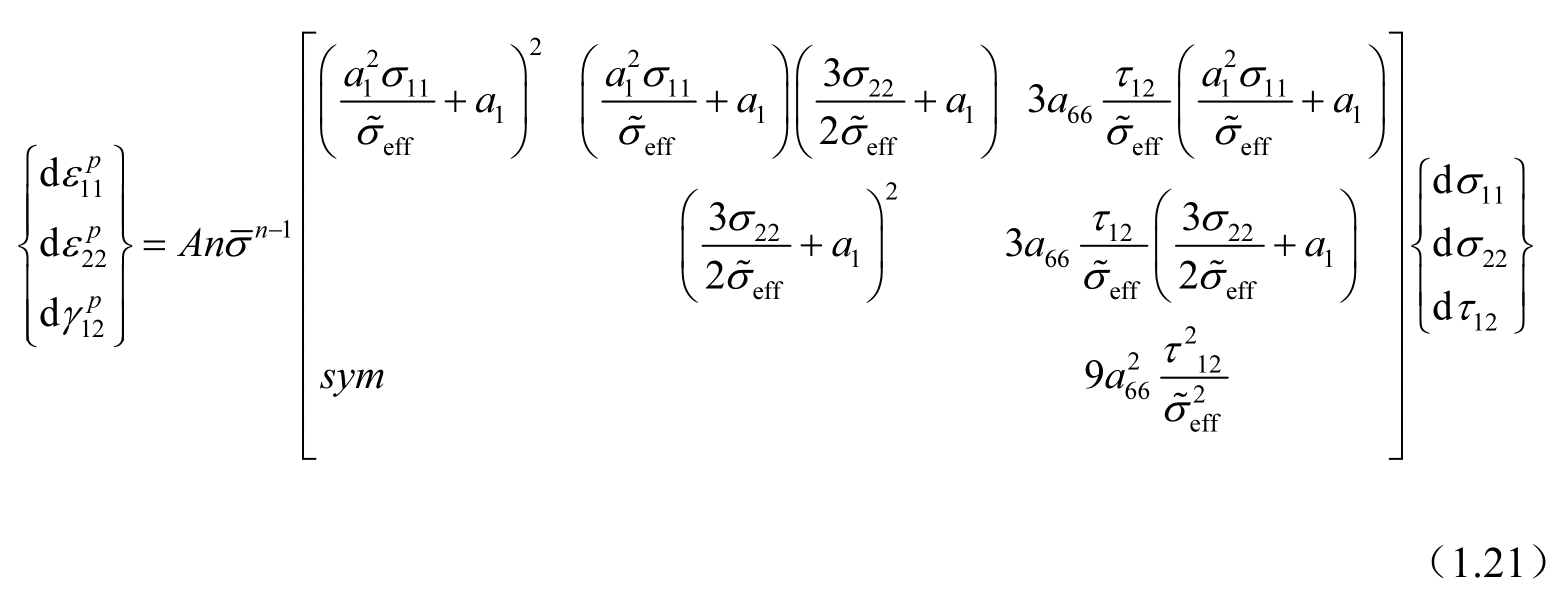
Yokozeki继续推导得到偏轴拉伸的本构关系模型,他制备了T800H/3633碳纤维/环氧复合材料来获取相关参数,制备了20层和40层的复合材料,进行了角度为15°、30°、45°、60°、90°的拉伸试验和压缩试验,通过压缩试验获得模型中的两个参数 a 1 和 a 66 ,得到的本构关系模型与试验数据相当吻合,可以很好地预测载荷方向上的非线性力学行为。
综上所述,第一类方法——增量法未能给出具体的本构关系,故本书的理论建模研究中不涉及该类方法,但在数值模拟时可以借鉴使用。第二类方法——Hahn-Tsai法及其演变,尤其是夏源明-杨报昌在Hahn-Tsai非线性弹性理论基础上导出的一般平面应力状态下的本构方程已经十分明确,其模型假定纵向线性,横向忽略不计,仅考虑1、2方向面内剪切对非线性的影响。Sun C.T.的模型考虑了剪切项和横向非线性的影响,但前提是假定纵向线性,而植物纤维由于其自身的特点在纵向上也表现出明显的非线性。Yokozeki的模型假定热固性复合材料在真应变范围以内纤维方向的塑性变形可以忽略不计,但他在模型中还是考虑了纵向方向上的应力对非线性的影响,能更好地预测纵向非线性,他只研究复合材料没有发生损伤、尚未屈服断裂之前的情况,采用了宏观力学法。因此,第一类方法——增量法中的Petit-Waddoups法、Hashin-Bagchi-Rosen法、Sandhu法、Jones-Nelson-Morgan法和Am ijima-Adachi法最终都需要使用增量法进行迭代,这可以在ABAQUS复合材料非线性有限元分析中采用该类增量法,直到得到收敛解时为止。第二类方法——Hahn-Tsai法及其演变可以在本书后续章节的研究中作为借鉴和参考。
总之,目前国内外针对复合材料如何建立非线性力学行为本构关系多采用宏观力学法,细观力学法多用于计算和预测强度,各种具体方法都有其适用范围。