





本节在观测站与目标分别在静止、匀速直线运动及匀加速直线运动的状态下,研究系统可完全观测、不可完全观测、完全不可观测的问题 [153-155] 。
假设观测站位置坐标为( x s , y s ) T ,目标位置坐标为( x , y ) T ,由 2.2.3 节定位方程可知,此时的观测方程为( x-x s ) 2 +( y-y s ) 2 = r 2 ,显然该方程没有唯一解,此时系统完全不可观测。
结论1: 当观测站静止、目标也静止时,系统完全不可观测。
证明: 极坐标系下目标的运动状态如图2-2所示,可列目标的状态方程如下:

式中, Φ ( k , k -1)表示系统的转移矩阵,其表达式为:
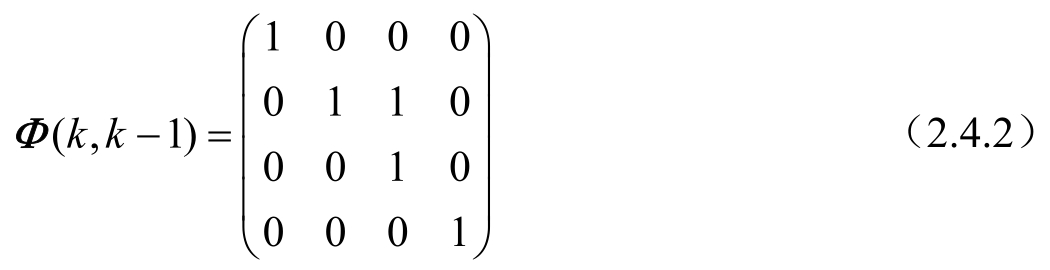
系统的观测方程为:

系统的Jacobian矩阵为:
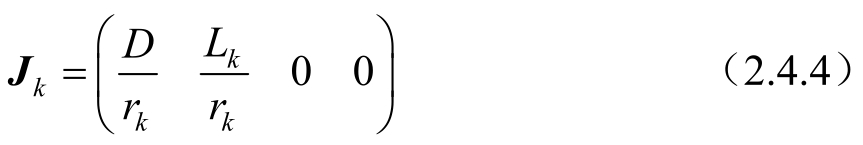
则系统的可观测矩阵为:
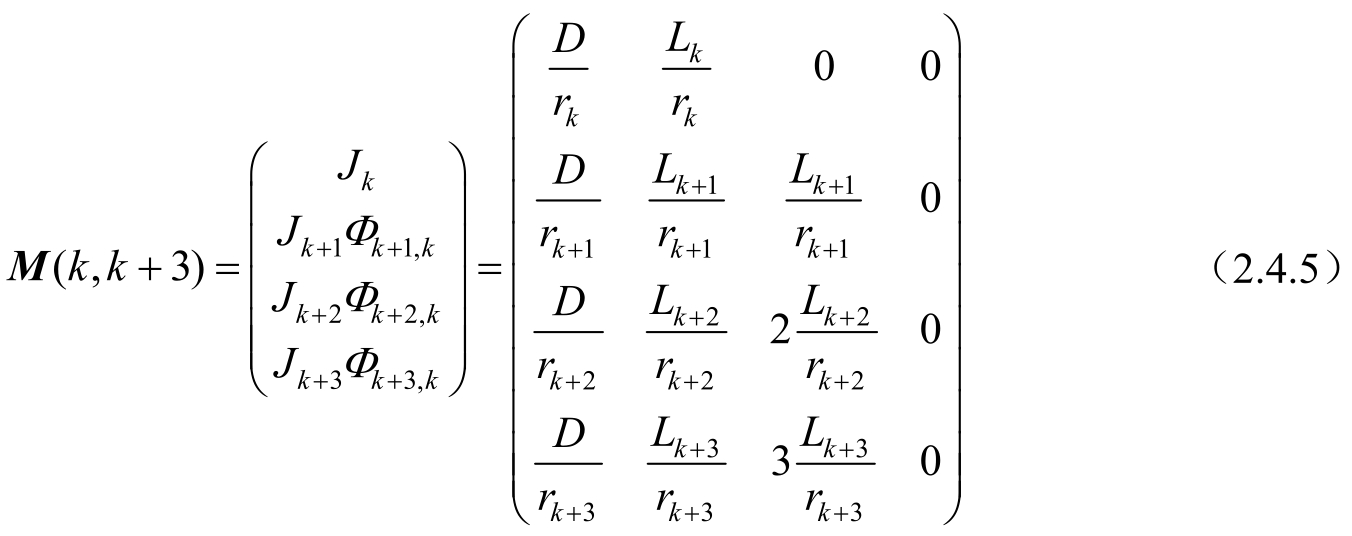
由式(2.4.5)计算可得det M ( k , k +3)=0,因此当观测站静止、目标匀速直线运动时,系统是不可观测的。
这一结论利用几何分析证明是很直观的:静止观测站对匀速直线运动目标的定位,其实是一组以观测站为圆心,以 t i 时刻测量距离 r i 为半径的同心圆, i =1,2,…, k , t i 时刻目标可能在对应圆上的任意一点,如图2-4所示。
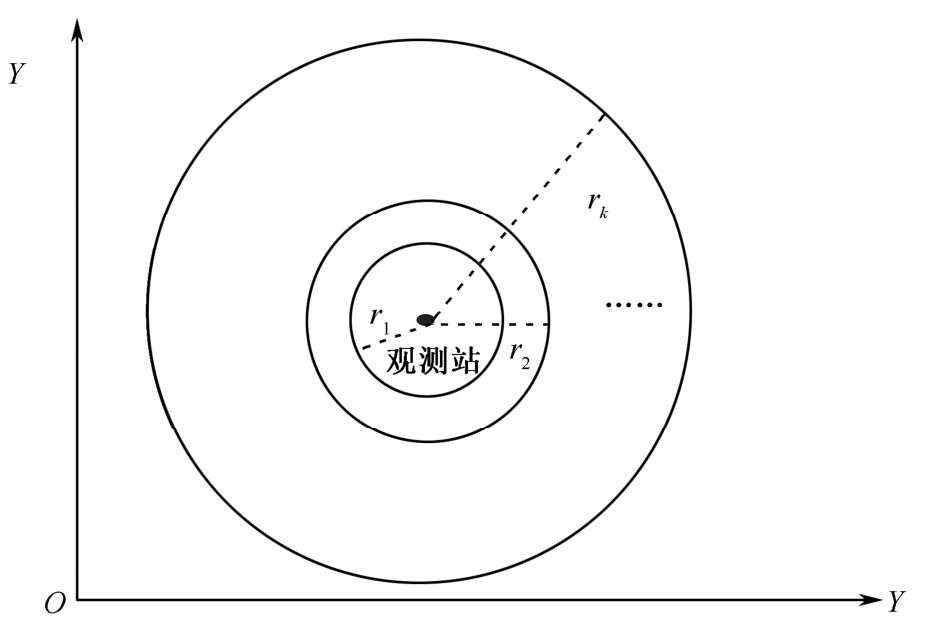
图2-4 静止观测站对匀速直线运动目标不可观测的几何说明
如果在已知目标做匀速直线运动的前提下,则其速度大小是可观测的,下面给出数学证明过程。
证明: 以观测站为极点建立极坐标系,如图2-5所示。
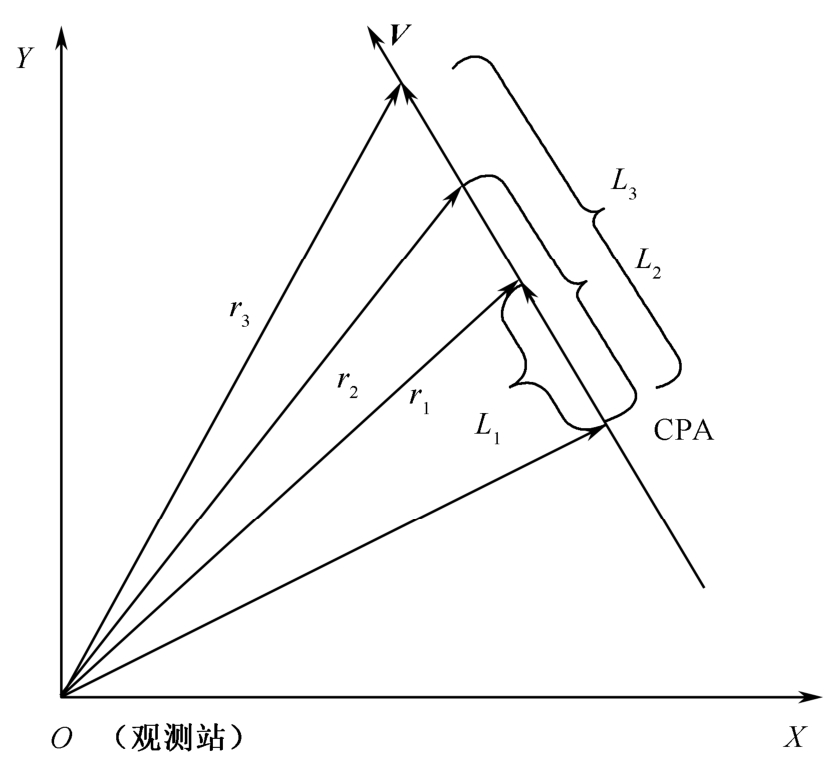
图2-5 静止观测站与匀速直线运动目标的几何关系(一)
以等时间间隔Δ T 进行观测,连续三次测距为 r 1 , r 2 , r 3 ,记观测站到航路捷径点CPA的距离为 r c , L 1 为第1次观测时目标位置到CPA的距离, L 2 为第2次观测时目标位置到CPA的距离, L 3 为第3次观测时目标位置到CPA的距离,以上均为标量。由勾股定理可得:

化简可得:

又因为目标做匀速直线运动,则有 L 2 -L 1 = L 3 -L 2 = d , d 为标量,表示测量时间间隔Δ T 内目标运动的距离。
将 L 2 = d + L 1 代入式(2.4.7),可得:

解上述方程组可得:

则速度大小:

若观测站和目标的相对运动轨迹如图2-6所示,运用勾股定理同样可得速度大小为
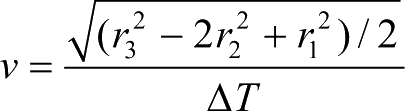 。
。
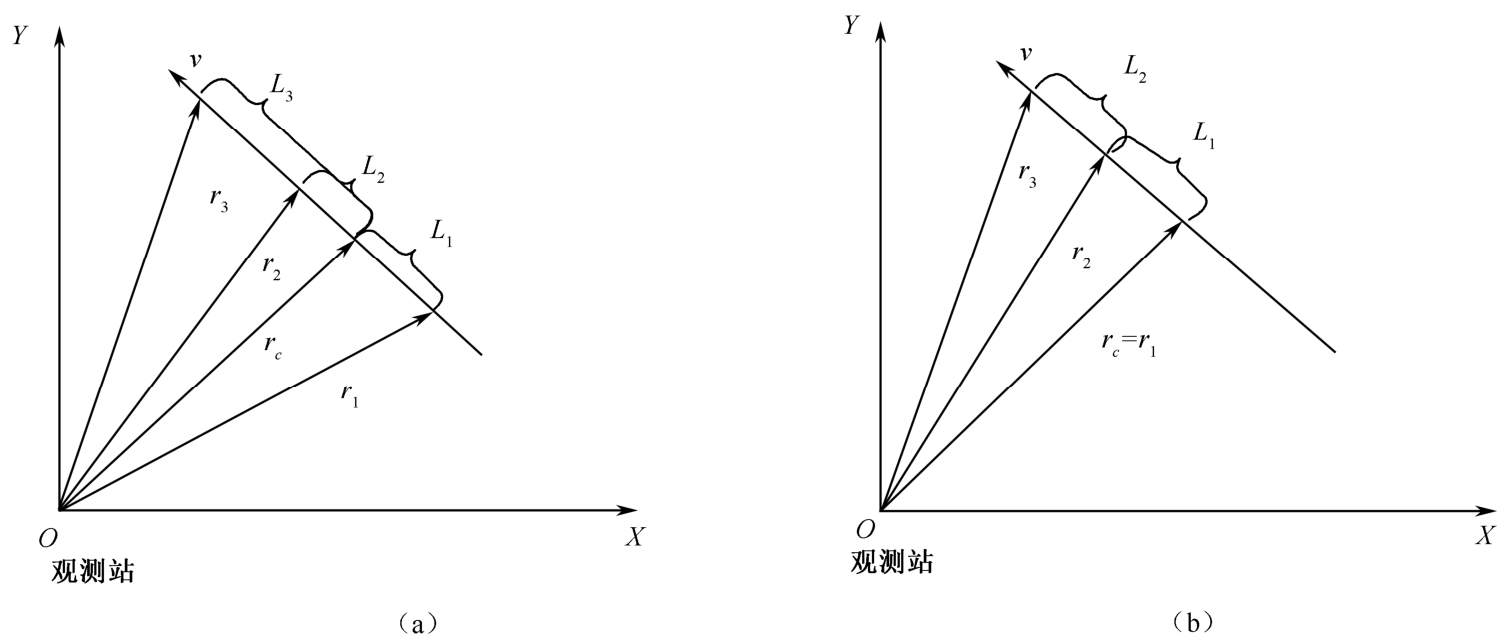
图2-6 静止观测站与匀速直线运动目标的几何关系(二)
结论2: 当观测站静止、目标做匀速直线运动时,系统不可完全观测,但匀速直线运动目标的速度大小是可知的。
证明: 极坐标系下目标的运动状态如图2-2所示,可列目标的状态方程如下:

式中,转移矩阵为:
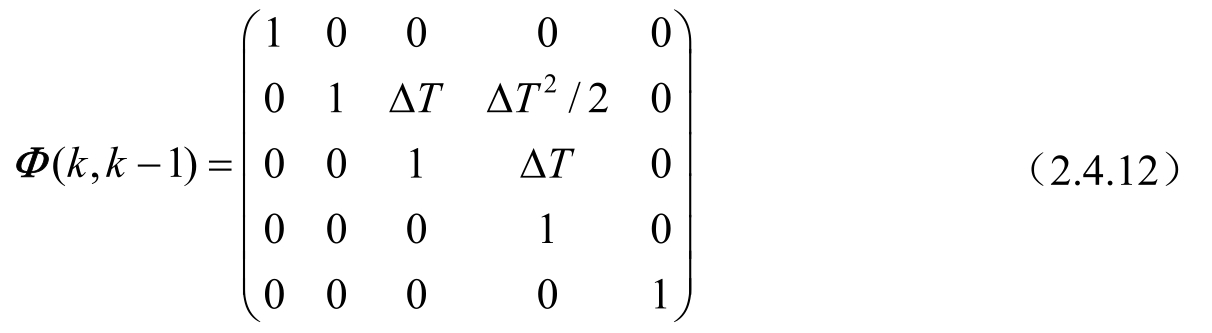
系统的观测方程为:

系统的Jacobian矩阵为:
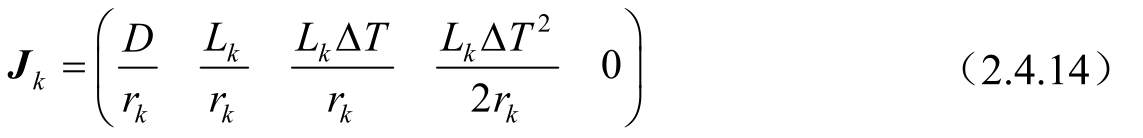
则系统的可观测性矩阵为:
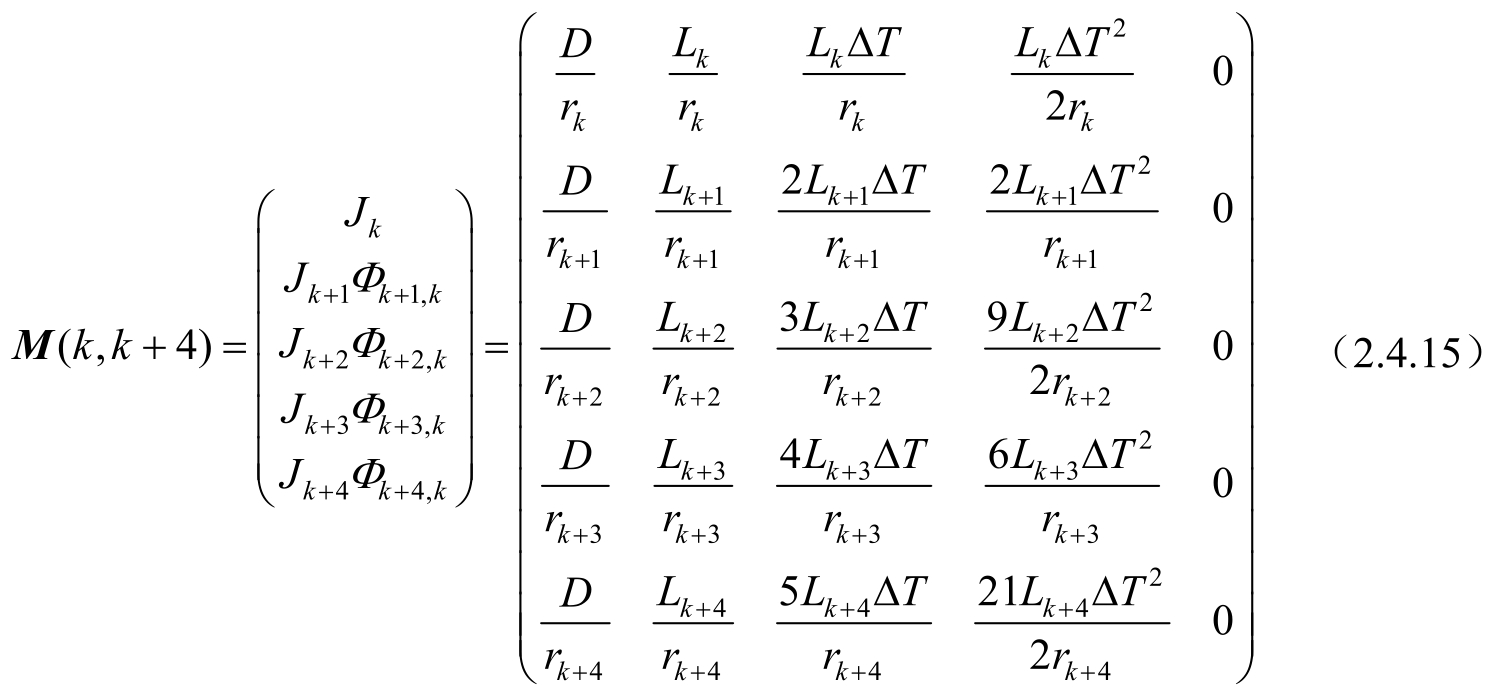
由式(2.4.15)计算可得det M ( k , k +4)=0,因此当观测站静止、目标做匀加速直线运动时,系统完全不可观测。
结论3: 当观测站静止、目标做匀加速直线运动时,系统完全不可观测。
情景1: 观测站始终做匀速直线运动。
假设观测站做匀速直线运动,速度为 V s ,初始航向角为 K s ,观测时间间隔为Δ T ,此时有:
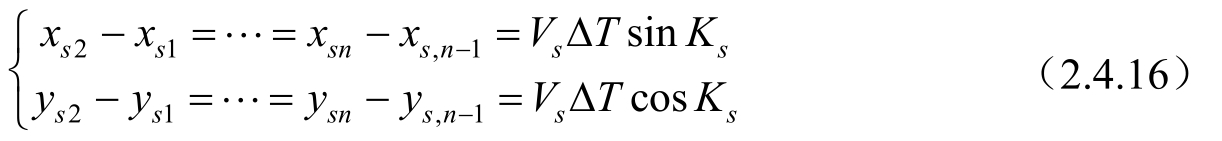
将式(2.4.16)代入式(2.3.6)可得:
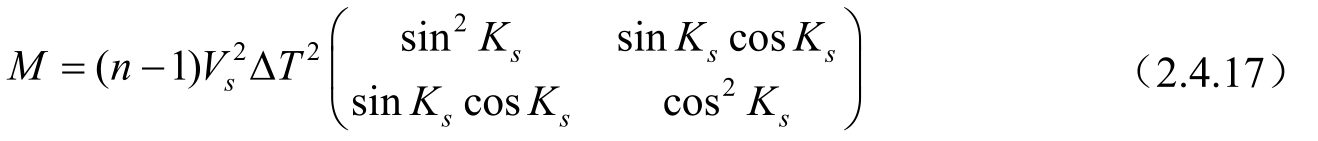
由式(2.4.17)计算可得det M =0,此时系统完全不可观测。不可观测的几何说明如图2-7所示。由图2-7可知,在观测站一直做匀速直线运动的条件下,静止目标可能的位置有2个,不满足可观测性的定义,因此,此时系统是完全不可观测的。
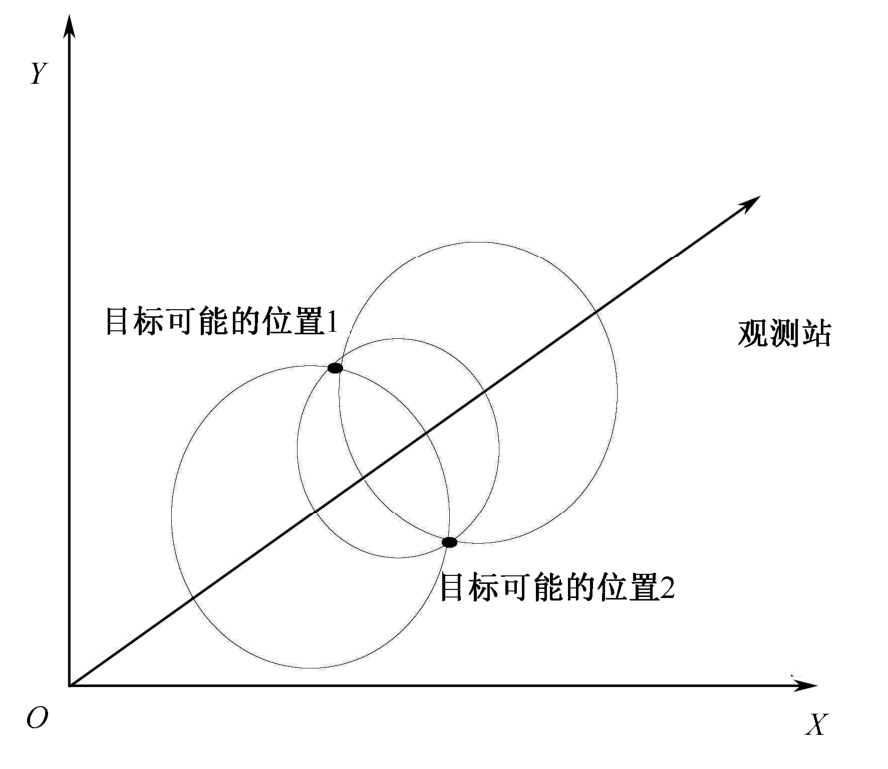
图2-7 匀速直线运动观测站对静止目标不可观测的几何说明
情景2: 观测站匀速直线运动一段时间后,进行机动转向。
假设观测站做匀速直线运动,速度为
V
s
,初始航向角为
K
s
,观测时间间隔为Δ
T
,若观测站在第
l
次观测时转向(1<
l
<
n
),
n
为总观测次数,转向后的速度变为
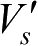 ,航向角变为
,航向角变为
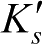 ,此时有:
,此时有:
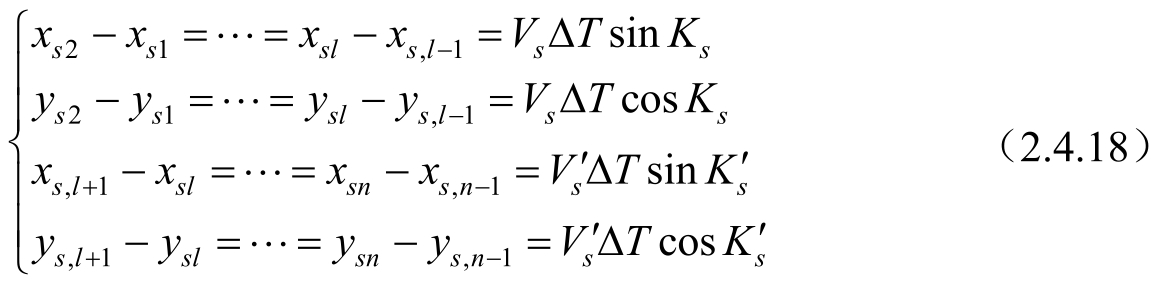
将式(2.4.18)代入式(2.3.6)可得:
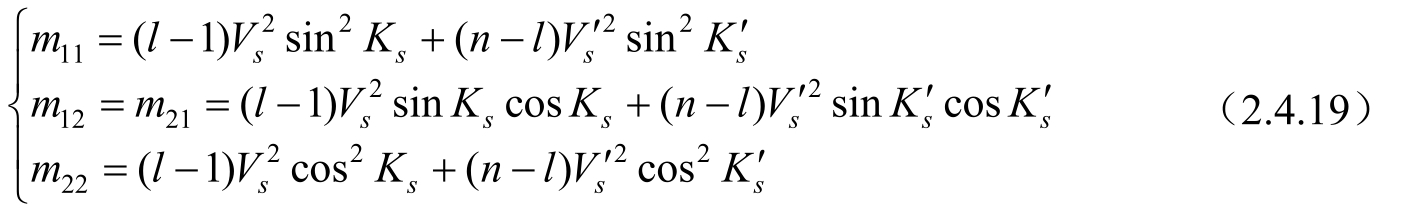
计算可得:
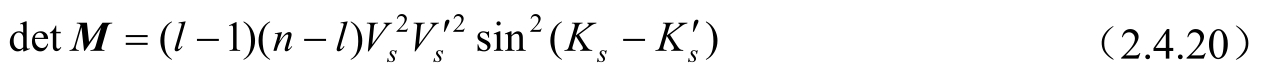
由于观测站进行了转向机动,即
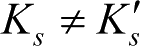 ,则det
M
≠0,此时系统可完全观测。
,则det
M
≠0,此时系统可完全观测。
情景3: 观测站匀速直线运动一段时间后,仅改变速度大小,不改变航向角。
由式(2.4.20)可知,当
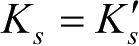 ,但
,但
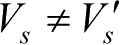 时,det
M
的值仍然等于零,说明匀速直线运动的观测站仅改变速度大小,不改变航向角度时,系统仍是完全不可观测的。不可观测的几何说明如图2-7所示,只是观测站转向前后观测的间隔距离不同,这里不再赘述。
时,det
M
的值仍然等于零,说明匀速直线运动的观测站仅改变速度大小,不改变航向角度时,系统仍是完全不可观测的。不可观测的几何说明如图2-7所示,只是观测站转向前后观测的间隔距离不同,这里不再赘述。
由情景1~情景3的结论可知,匀速直线运动的观测站只有在观测过程中进行机动转向,系统才可观测。
上述分析过程也可以通过几何作图法进行说明,如图2-8所示。在二维情况下,直线运动(非径向运动)的观测站利用距离对静止目标进行观测的几何图形表示,相当于以观测站在某一时刻的位置为圆心,观测距离为半径作圆。 k 次( k 为自然数)观测后,以 k 次观测距离为半径的 k 个圆相交于以观测站航迹为对称轴的两点,此时不能得到唯一的目标位置坐标,此时目标不可观测,如情景1;即使目标进行变速运动,比如情景3,目标仍然不可观测。但是,如果在观测站做一次转向后进行观测,以观测站位置为圆心,以观测距离为半径作圆,会交于变向之前的两点中的一点,如图中的 A 点,此时会得到目标的唯一坐标,如情景2。
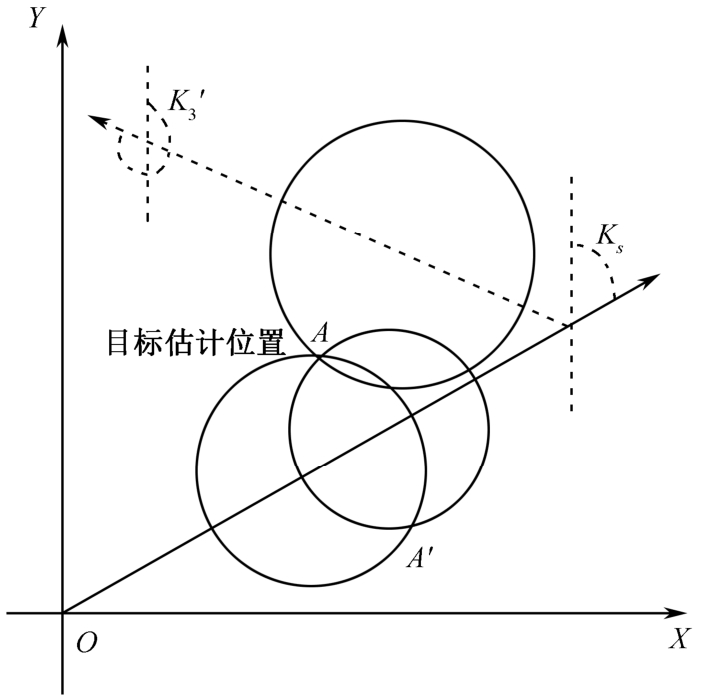
图2-8 观测站转向对静止目标可观测性的几何说明
情景4: 若目标在观测站匀速直线运动轨迹的延长线上,即观测站做关于目标的径向运动时,系统完全可观测。
可观测的几何说明如图2-9所示。
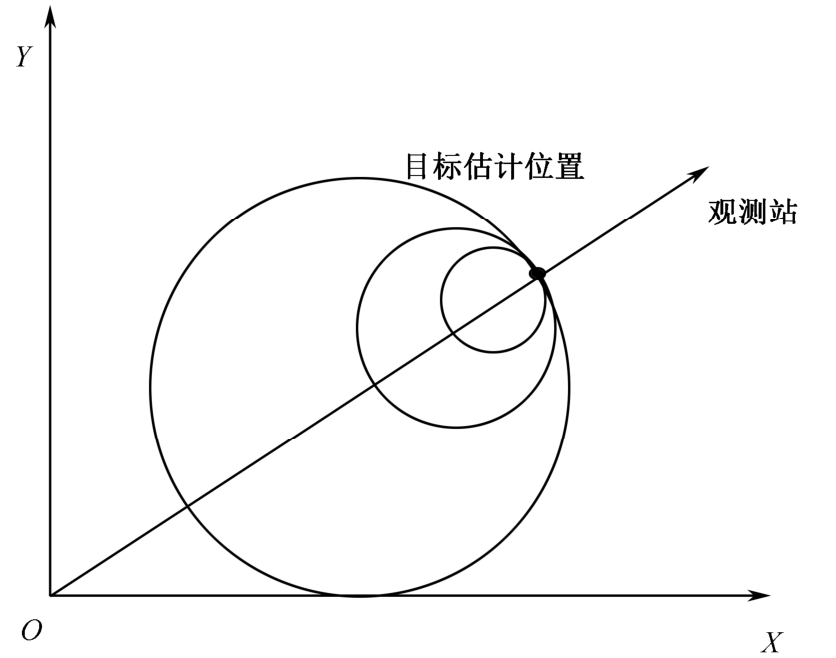
图2-9 直线运动观测站对静止目标可观测的几何说明
结论4: 当观测站做匀速直线运动、目标静止时:①若观测站做关于目标的非径向直线运动,则系统完全不可观测;②若观测站在观测过程中进行转向机动,则系统完全可观测;③若观测站做关于目标的径向直线运动,则系统完全可观测。
假设匀速直线运动的观测站运动速度为 V s ,匀速直线运动的目标运动速度为 V m ,在2.4.2节与2.4.4节研究结论的基础上,根据相对运动理论可以得到如下结论:
结论5: 若 V s >> V m ,可以近似于观测站做匀速直线运动、目标静止的情况,由结论4可知,①若观测站做关于目标的径向直线运动时,则系统完全可观测;②若观测站进行机动转向,则系统可完全观测;③若观测站做关于目标的非径向直线运动,则系统完全不可观测。
结论6: 若 V s << V m ,可以近似于观测站静止、目标做匀速直线运动时的情况,由结论 2 可知,此时系统不可完全观测,但匀速直线运动目标的速度大小可知。
结论7: 一般情况下,系统完全不可观测;若观测站进行转向机动,则系统可完全观测。
特殊情形: 等时间间隔Δ T 进行观测,若量测距离 r i 恒相等,说明观测站与目标做同向同速的匀速直线运动,目标可能的运动轨迹如图2-10所示。
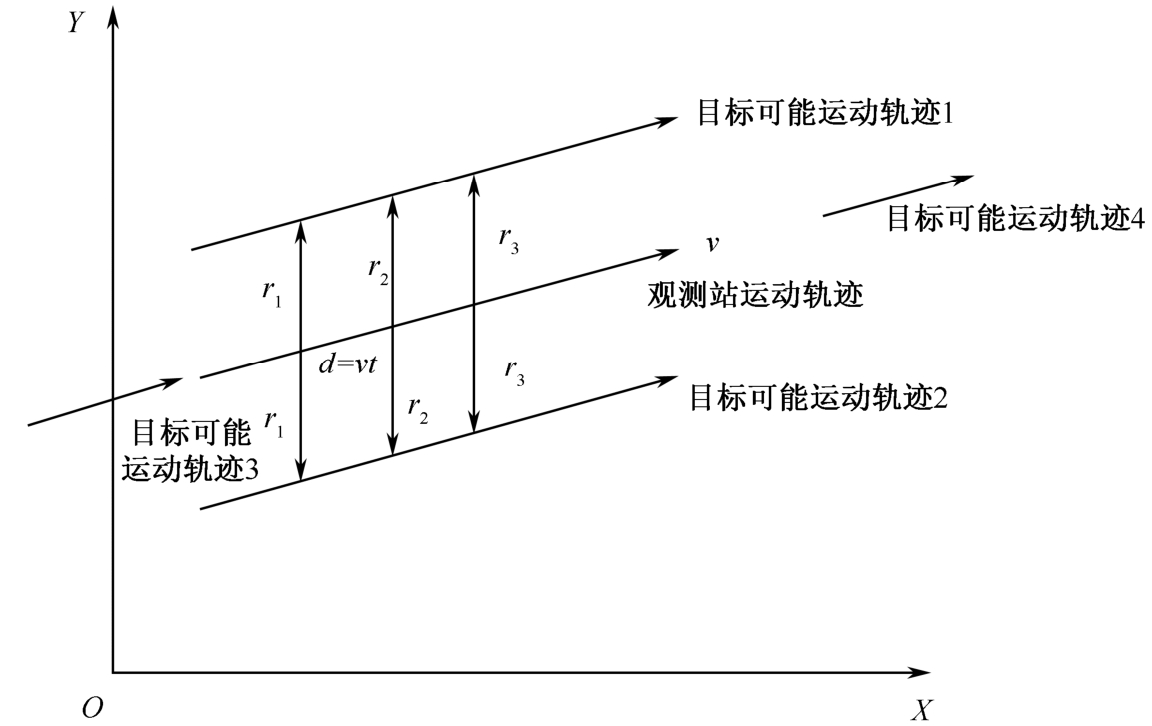
图2-10 匀速直线运动观测站对匀速直线运动目标的几何说明
结论8: 当观测站与目标都做匀速直线运动时,若量测距离恒相等,说明目标与观测站同向同速,即此时系统不可完全观测。
假设观测站做匀速直线运动,速度为 V s ;目标做匀加速直线运动,初速度为 V m ,加速度为 a m 。在 2.4.3 节结论的基础上,根据相对运动理论可以得到如下结论:
结论9: 一般情况下,可以近似于静止的观测站,对以相对初速度为 V m -V s ,加速度为 a m 的匀加速直线运动目标的观测,系统完全不可观测。
假设目标静止;观测站做匀速直线运动,速度为 V s ,加速度为 a s 。此时有:
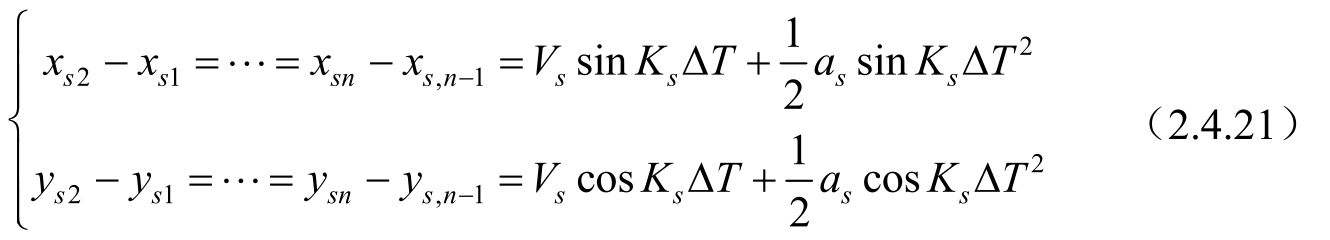
将式(2.4.21)代入式(2.3.6)可得:
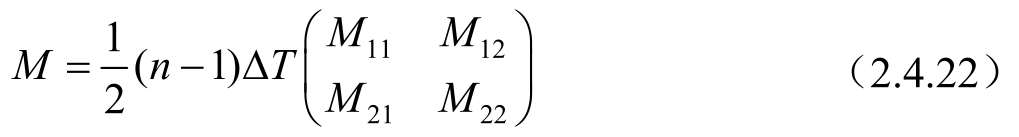
式中:
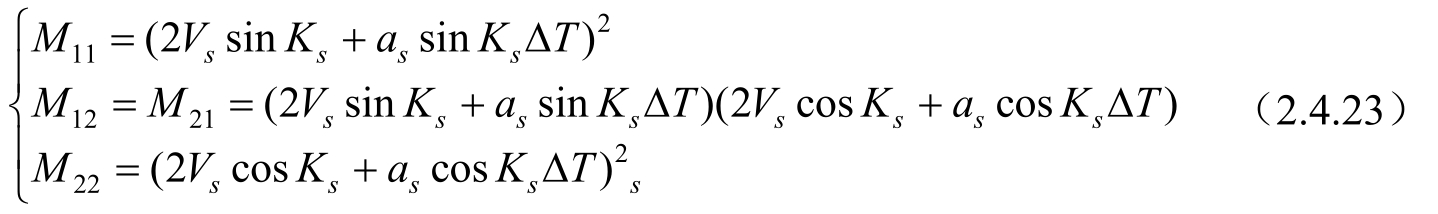
由式(2.4.23)计算可得det M =0,此时系统完全不可观测。若观测进行机动转向,则系统可完全观测;若观测站做关于目标的径向运动时,则系统可完全观测。几何说明同图2-7、图2-8相似,只是观测站连续两次观测时间隔的距离不同,这里不再赘述。
结论10: 观测站匀加速直线运动、目标静止时,观测站转向机动可完全观测;若观测站做关于目标的径向运动时,则系统可完全观测。
结论11: 匀加速直线的观测站对匀速直线运动的目标进行观测时,系统可观测。
证明: 定义向量 X ( t )=[ r V m sin K m -V w sin K w V m cos K m -V w cos K w ] T 为纯距离系统在直角坐标系下的状态变量,则系统动态方程为:
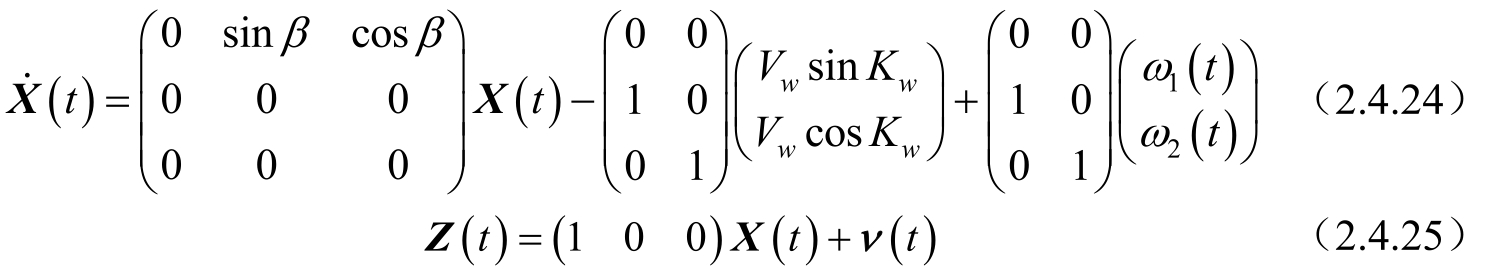
其转移矩阵为:
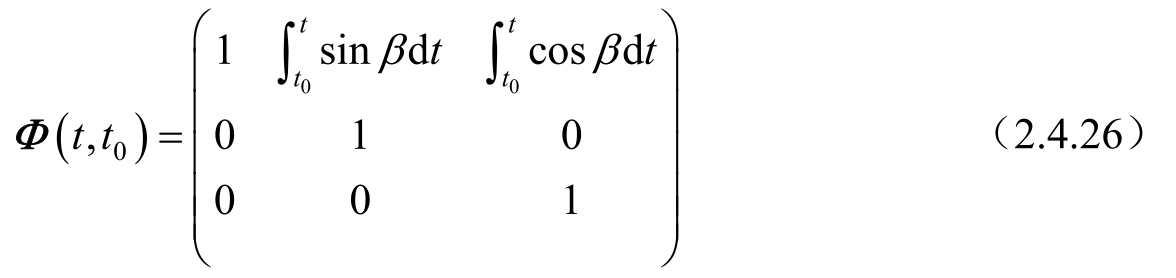
该动态方程从形式上看是状态 X ( t )的线性方程,实际上,由于系统矩阵包含未知量 β ,而 β 又是被估状态的函数,所以动态方程仍然是 X ( t )的非线性方程,测量方程是 X ( t )的线性方程。动态方程的这种特定的形式,可以按照带有未知变量的线性方程来处理。
按照线性时变系统来考虑可观测性情况 [156] 。在线性时变系统中,令:
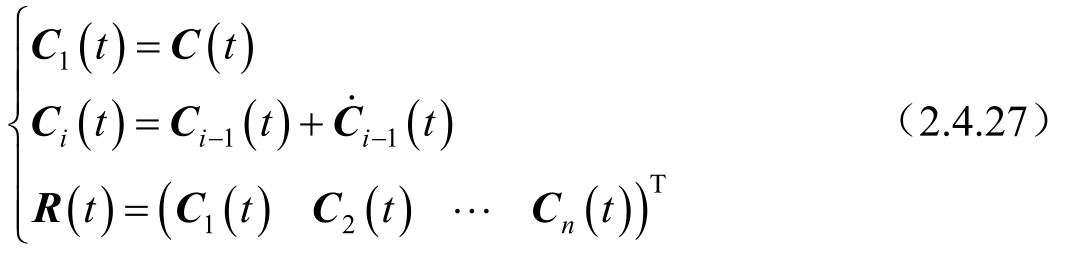
如果存在某个时刻
t
f
>0,使得rank
R
(
t
f
)=
n
,则系统在
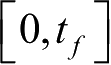 上是可观测的。在本系统中:
上是可观测的。在本系统中:
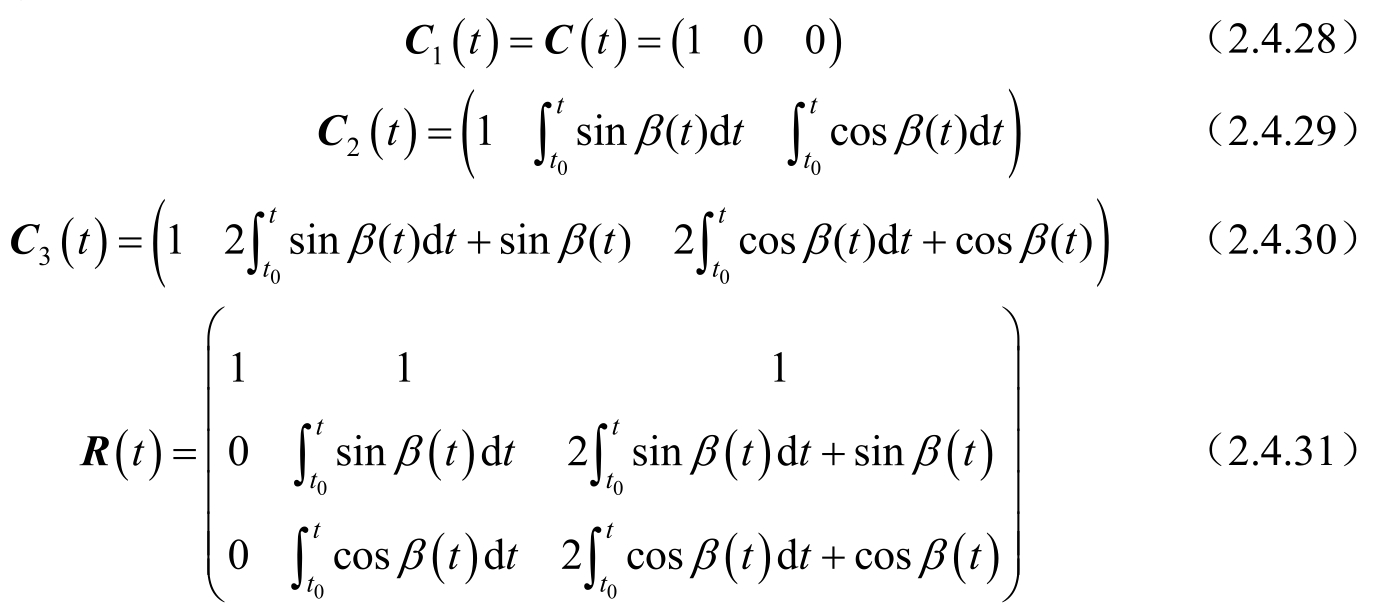
经计算可得:
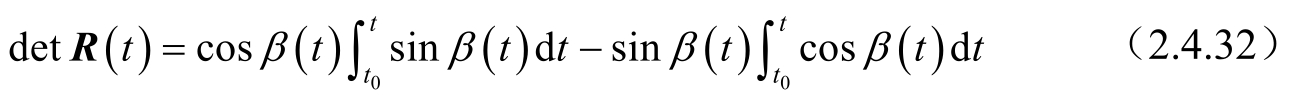
现令det R ( t )=0,可得:

对于
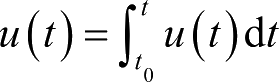 型的积分,只有当
u
(
t
)取指数函数时,才满足上述等式,因此det
R
(
t
)≠0,rank
R
(
t
)=
n
,即目标做匀速直线运动、观测站做匀加速直线运动时的纯距离系统是可观测的。
型的积分,只有当
u
(
t
)取指数函数时,才满足上述等式,因此det
R
(
t
)≠0,rank
R
(
t
)=
n
,即目标做匀速直线运动、观测站做匀加速直线运动时的纯距离系统是可观测的。
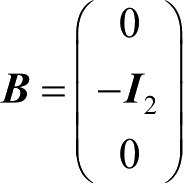
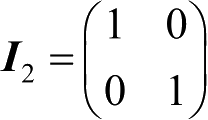
假设目标在直角坐标系下做匀加速运动,观测站也做匀加速运动,连续形式的系统方程和观测方程为:
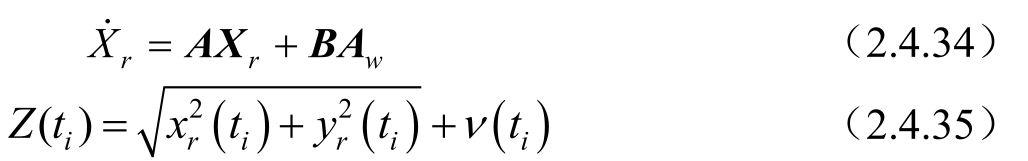
式中,
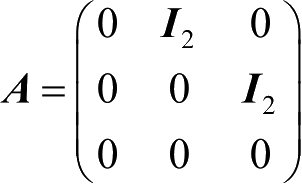 ;
;
 ;
;
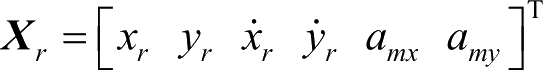 ;
;
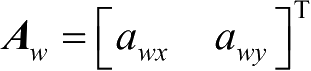 ;
;
 。
。
在向量
X
r
中,
x
r
与
y
r
分别表示目标与观测站之间相对位置的
X
轴分量与
Y
轴分量;
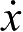 与
与
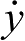 分别表示目标与观测站之间相对速度的
X
轴分量与
Y
轴分量;
a
mx
与
a
my
分别表示目标常加速度的
X
轴分量与
Y
轴分量。在向量
A
w
中,
a
wx
与
a
wy
分别表示观测站加速度的
X
轴分量与
Y
轴分量。
分别表示目标与观测站之间相对速度的
X
轴分量与
Y
轴分量;
a
mx
与
a
my
分别表示目标常加速度的
X
轴分量与
Y
轴分量。在向量
A
w
中,
a
wx
与
a
wy
分别表示观测站加速度的
X
轴分量与
Y
轴分量。
根据线性定常系统的解公式,可以得到:
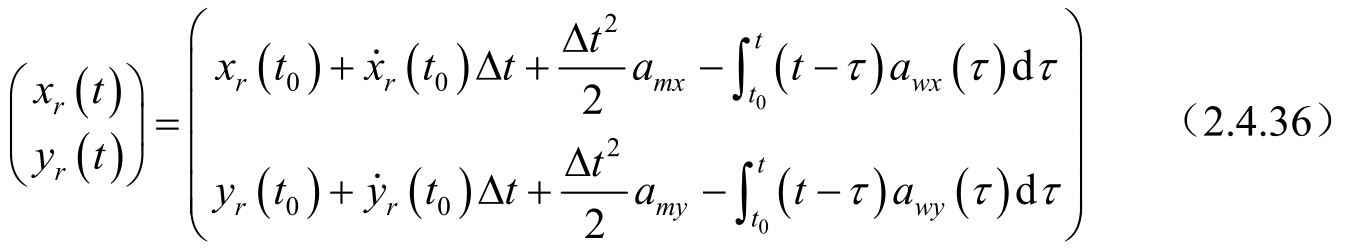
定义
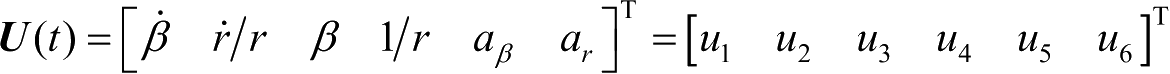 为修正极坐标系下的状态变量;根据直角坐标系和修正极坐标系下解的一一对应关系,可以得到在修正极坐标下状态变量的解。
为修正极坐标系下的状态变量;根据直角坐标系和修正极坐标系下解的一一对应关系,可以得到在修正极坐标下状态变量的解。
修正极坐标系下,观测方程可以写成:
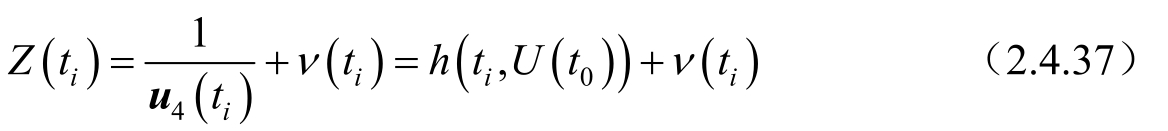
观测向量可表示为:
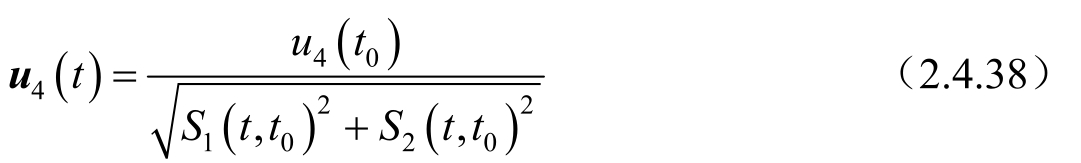
式中:
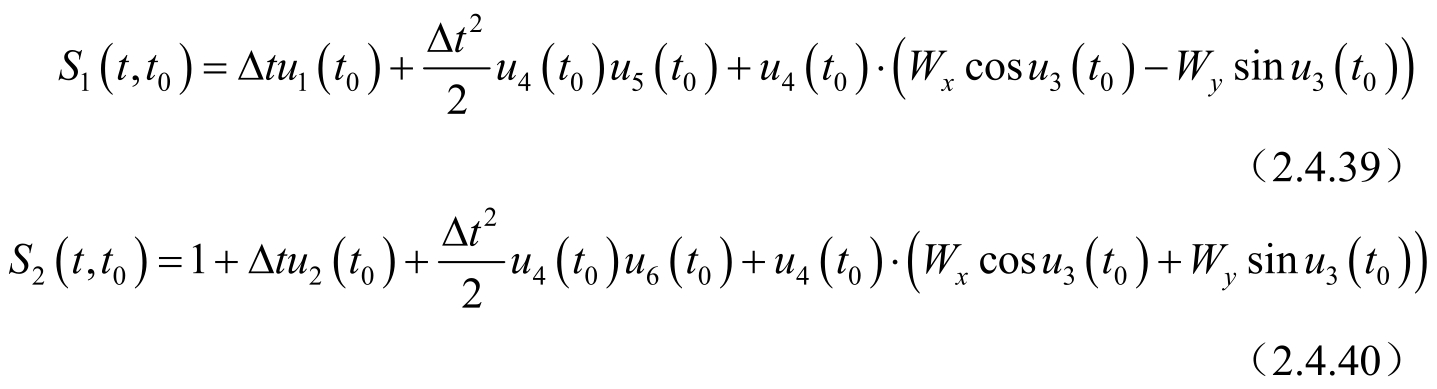
式中:

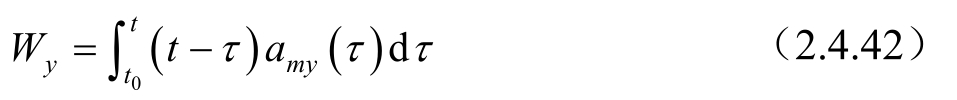
利用Fisher信息阵,在 U ( t 0 )已知的情况下,判断系统的可观测性,其中Fisher信息阵为:
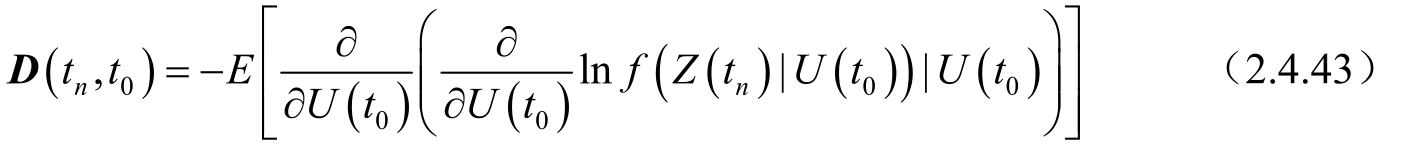
式中:
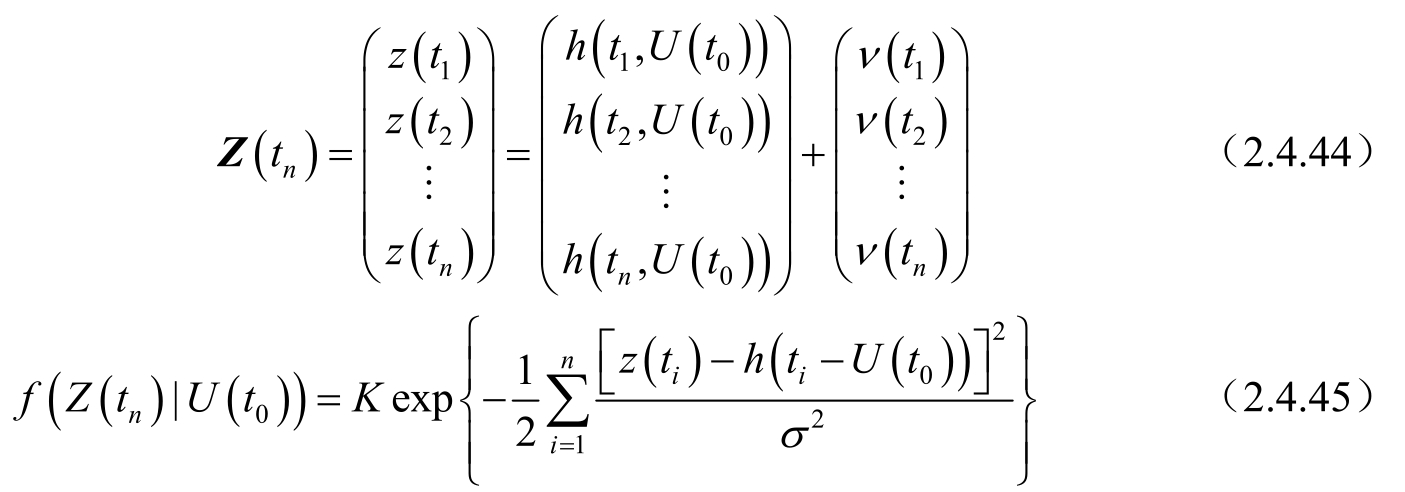
K 是规一化常数,此时 J ( t n , t 0 )可写成:
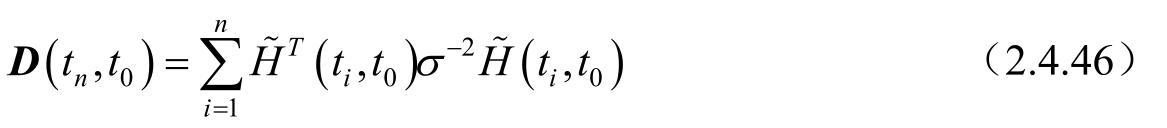
式中:
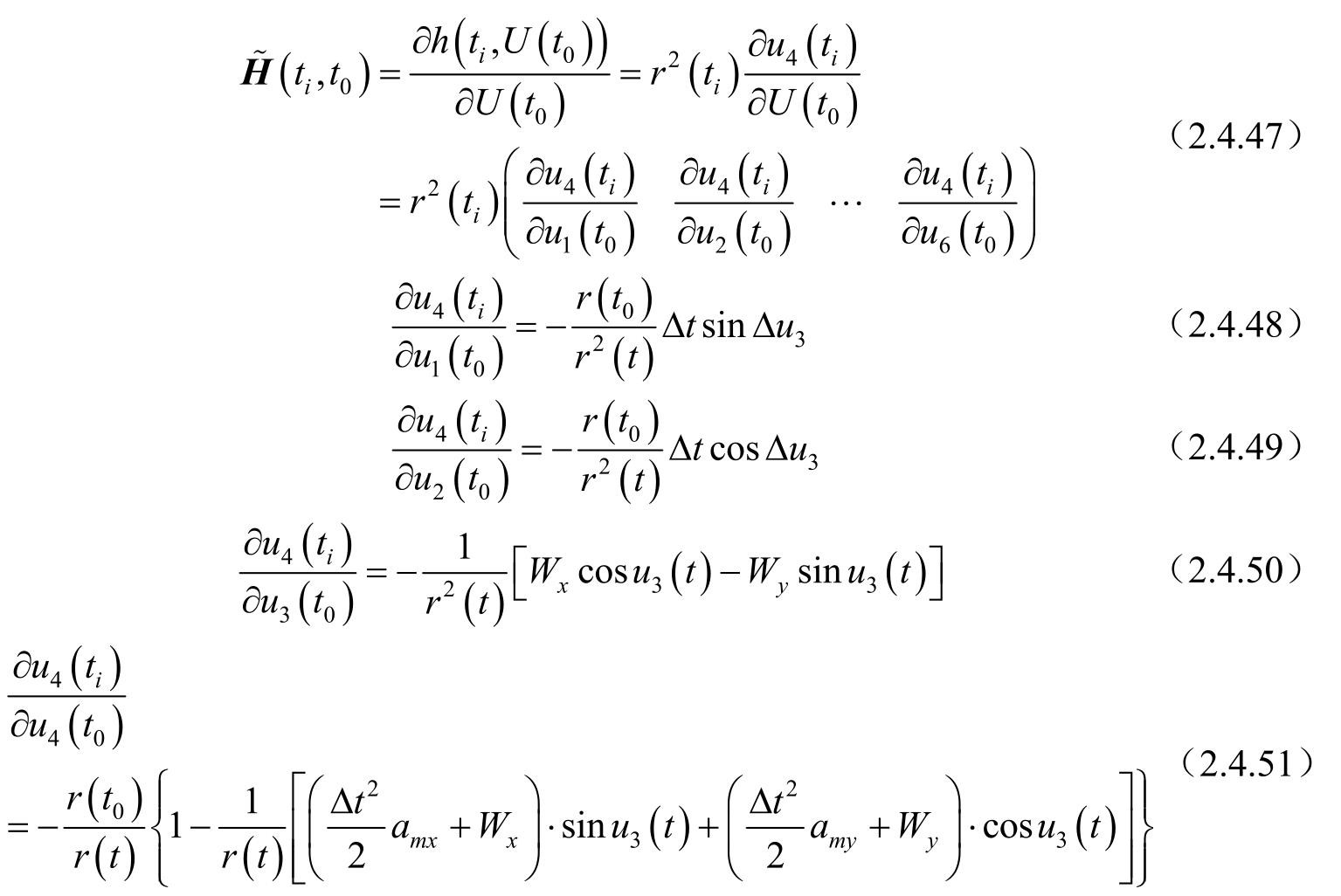
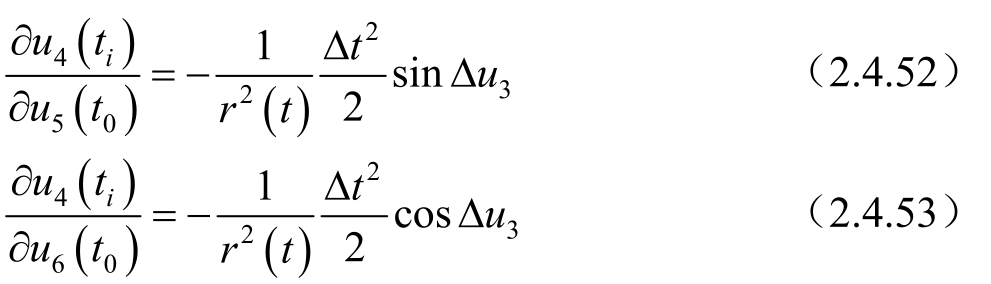
若想得到系统的可观测性,只需Fisher信息阵正定,即Fisher信息阵各列互不相关,即存在任意非零常数矩阵 μ ,只须满足:

即:
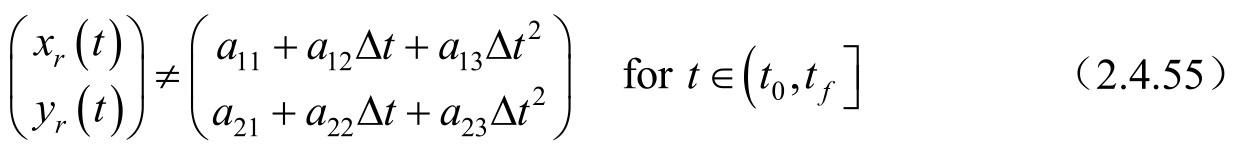
式中, a ij ( i =1,2; j =1,2,3)表示任意不全为零的常数。
结论12: 目标与观测站均做匀加速运动时,如果目标与观测站的相对运动轨迹是一条方位角恒定的轨迹,或者观测站以常速或常加速度运动,则系统是不可观测的;也就是说观测站在纯距离的测量条件下跟踪一个常加速度的运动目标,应进行非零的机动。
在此基础上,如果目标进行匀速直线运动,即目标加速度为0,这时式(2.4.55)可以变形为:
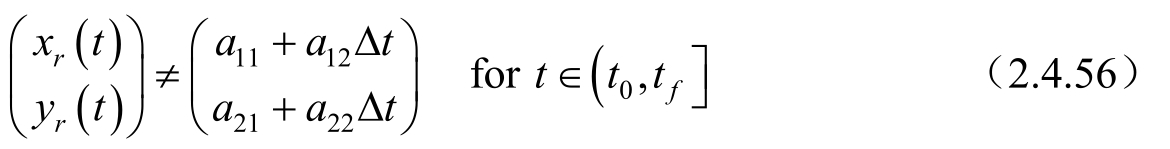
式中, a ij ( i =1,2; j =1,2,3)表示任意不全为零的常数。该式说明,观测站匀加速运动、目标匀速直线运动,系统可观测。图2-11说明了与式(2.4.55)相违背时系统不可观测的情况。
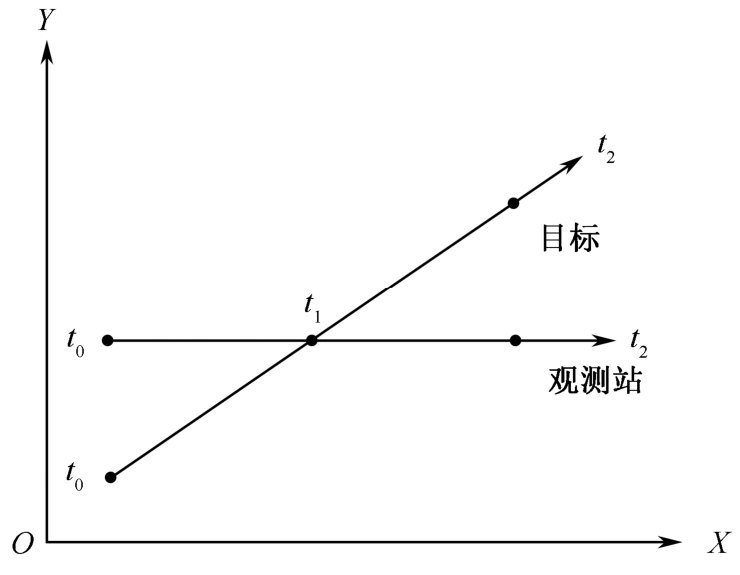
图2-11 系统不可观测的情况说明
结论13: 二维纯距离和/或各阶变化率系统,在目标匀速直线运动的假定下,即当 V m ≠0,要同时求解 β , V m , K m 的必要条件为约束输入变量至少是4个。
证明:
情况 1 :仅输入 r 时,可列出方程组
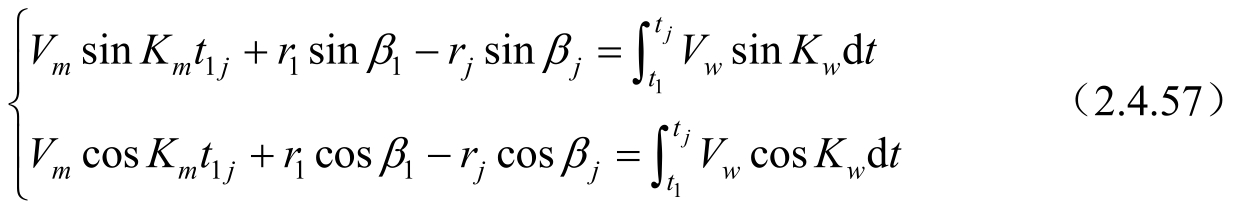
量测次数、约束输入变量个数、方程个数和未知量个数的关系如表2-1所示。
表2-1 量测次数、约束输入变量个数、方程个数和未知量个数的关系

由表2-1可得,能同时解出 β , V m , K m 的必要条件是2( k -1)≥ k +2,解该不等式可得 k ≥4。
情况2: 当 r 和其各阶导数作输入量时,由于 V w ( t )和 K w ( t )是连续可微函数,所以 r ( t )也是连续可微函数,因此可以把 r 的各阶导数看作下列表达式的极限,如表2-2所示。
表2-2 距离各阶变化率与差分极限的关系

而Δ t j = t-t j 是可控输入,所以按照上面导数与差分式的对应关系,增加 r 的一阶导数时,就相当于增加了一个新的距离,由于距离不得少于4个,所以当 r 及其导数作输入量时,其距离及其导数的总数不得少于4个。
通过上述证明过程,结论13成立。