




 1.2 智能工厂设备常见算法
1.2 智能工厂设备常见算法
模糊控制的主要思想是在控制中引入模糊控制理论,从而作用于难以建立数学模型和缺乏精确模型的复杂系统。模糊控制不依赖于精确的数学模型,而是通过总结知识和积累经验对复杂的系统进行控制,因而对具有不确定性对象的系统具有很强的适应能力。简而言之,模糊控制理论就是模仿人的思维方式和经验来实现自动控制的一种控制方法。
1.模糊集合
模糊集合的概念是美国加州大学Zadeh教授通过隶属度函数于1965年在他的《Fuzzy Sets》等著名论著中首先提出来的。1973年,他在文章中又引入了“语言变量”的概念,相当于一个变量定义模糊集合。1985 年,Takagi 和Sugeno 提出了Takagi-Sugeno模糊模型,此模型的主要特点是通过线性系统模型来表达每一个模糊规则的特性。
模糊集合是指具有隶属度的元素的集合,它是一个普通集合的扩展。在普通集合中,元素的隶属度以二进制形式表示,即一个元素必须属于或不属于一个集合。相反,模糊集合理论允许评估一个元素在集合中的函数隶属度,通过增加一个介于[0,1]之间的隶属度函数值来描述。普通集合是模糊集合的特殊情况,因为当模糊集合的隶属度取0或1时就是普通集合。模糊集合理论可以用于信息不完整或不精确的广泛领域内。
A是定义在集合X上的一个模糊子集,则用下面的映射表示集合X上的模糊子集
A:X→[0,1]
x→μ A (x)
其中,μ A 为模糊子集A的隶属函数,μ A (x)表示x属于模糊子集A的程度,即隶属度,其值介于[0,l]之间。当μ A (x)为0时,表示x不包含于A;当μ A (x)为1时,表示x包含于A;当μ A (x)介于0和1之间时,则表示x属于A的程度。
一般来讲,模糊集合用向量法来表示。如果模糊集合A的论域由有限个元素组成,那么可以用下面的形式来表示模糊集合A
A=[μ A (x 1 ),μ A (x 2 ),…,μ A (x n )]
可以简化表示为
A=[x 1 ,x 2 ,…,x n ]
2.模糊集合的隶属度函数
模糊集合的隶属度函数是普通集合中指标函数的概括。在模糊逻辑中,它代表了在一个评估范围内的真实程度。尽管在概念上截然不同,但是人们通常将真实性与概率相混淆。模糊真实性代表了定义在模糊集合中的隶属度,而不是某些事件或条件的可能性。
正确地构造隶属度函数是控制效果好坏的关键,因为每个人对模糊概念的认识不同,所以确定隶属度函数存在主观性。确定隶属函数的方法如下。
1)模糊统计法
x 0 是论域U上的确定元素,而A 1 是论域U上的可变动的清晰集合,要判断x 0 是否完全属于集合A 1 ,对于不同的实验者确定A 1 的边界是不同的,但是它们都应用于同一个集合A。因此,模糊统计法的执行步骤是:x 0 固定而A 1 可变,重复做n次实验,就可以得到隶属频率。随着n的增大,隶属频率趋于稳定,那么稳定时的隶属频率就是x 0 对A的隶属度。这种方法的缺点是计算量比较大。
2)例证法
已知有限个隶属度μ A 的值,估计论域U上模糊子集A的隶属度函数。如果论域U代表温度,A是“今天的平均温度高”,那么A是U的一个模糊子集,为了确定μ A 的值,首先选取一个温度值w,然后选取几个语言真值中的一个来回答今天的平均温度是否高。语言变量分别选取“真”、“似真似假”、“假”3种情况,并且用数字1、0.5、0来表示以上3个语言真值。记录n天的平均气温w 1 ,w 2 ,…,w n ,即可得到A的隶属度函数的离散表示方式。
3)专家经验法
一般通过实际经验来确定隶属度函数。在通常情况下,这类隶属度函数都是比较粗略的,要经过不断地实验来完善和修改。
表示隶属度函数的常用方法有抛物线形、直线型的三角形和梯形等,在实际应用中,一般三角形以其直观、方便被普遍采用。
3.模糊控制规则
1)模糊控制规则的表示
模糊规则是由语言变量所表达的模糊条件语句所组成的,例如,模糊规则可以表示成“如果房间变热,将风扇叶片的旋转速度加快”,这里的房间温度和风扇叶片旋转速度都是不精确的数量。“热”和“快”都是模糊术语。模糊逻辑和模糊规则可以增加类似于人类的主观推理能力。
如果一个被控对象的输入变量为A和B,输出为C,那么模糊规则可以用以下形式的条件语句表示
IFxisAANDyisBTHENzisC
其中,x、y和z是语言变量。
2)模糊控制规则的制定
模糊规则可以根据专家的知识和经验进行归纳总结并编写,它直接影响着控制系统的质量,因此,编写一套合理的模糊规则非常重要。经验总结就是经过加工、整理和提炼,去除粗略规则的同时保留精确规则,然后制定模糊规则的方法。此方法比较简单和直接,并且易于实现。
模糊控制一般用于无法以严密的数学表示的控制对象模型,即可利用人(熟练专家)的经验和知识来很好地控制。因此,利用人的智力模糊地进行系统控制的方法就是模糊控制,其控制原理图如图1-3所示。
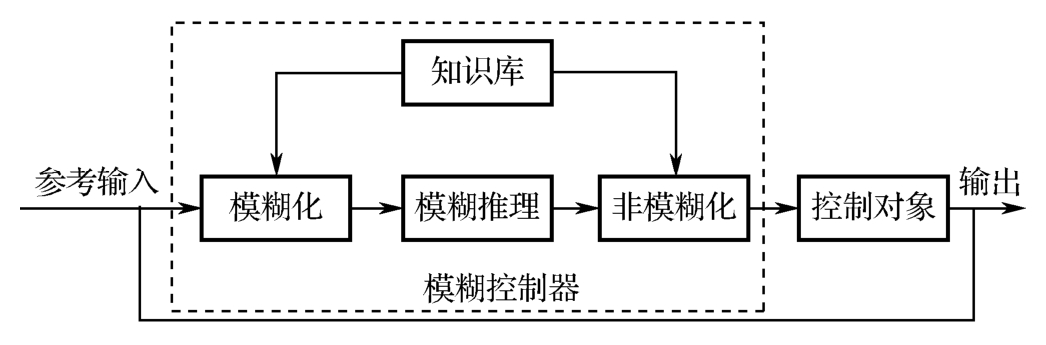
图1-3 模糊控制原理图
人工神经网络(Artificial Neural Netw orks,ANN)算法是一种普遍而且实用的方法,在样例中学习值为实数、离散或向量的函数。ANN算法对于训练数据中的错误鲁棒性很好,且已经成功地应用到智能工厂中的很多领域,如PID控制、噪声分类、振动分析、机器人控制等。
1.人工神经网络的定义
人工神经网络是由大量处理单元(人工神经元)广泛互连而成的网络,是对人脑的抽象、简化和模拟,反映人脑的基本特征。它按照一定的学习规则,通过对大量样本数据的学习和训练,抽象出样本数据间的特性—网络掌握的“知识”,把这些“知识”以神经元之间的连接权和阈值的形式储存下来,利用这些“知识”可以实现某种人脑的推理、判断等功能。
一个神经网络的特性和功能取决于3个要素:构成神经网络的基本单元,即神经元;神经元之间的连续方式,即神经网络的拓扑结构;用于神经网络学习和训练,修正神经元之间的连接权值和阈值的学习规则。
2.神经元
人工神经元是对生物神经元功能的模拟。人的大脑中大约含有10 11 个生物神经元,生物神经元以细胞体为主体,有许多向周围延伸的不规则树枝状纤维构成的神经细胞,其形状很像一棵枯树的枝干。生物神经元主要由细胞体、树突、轴突和突触组成,如图1-4所示。
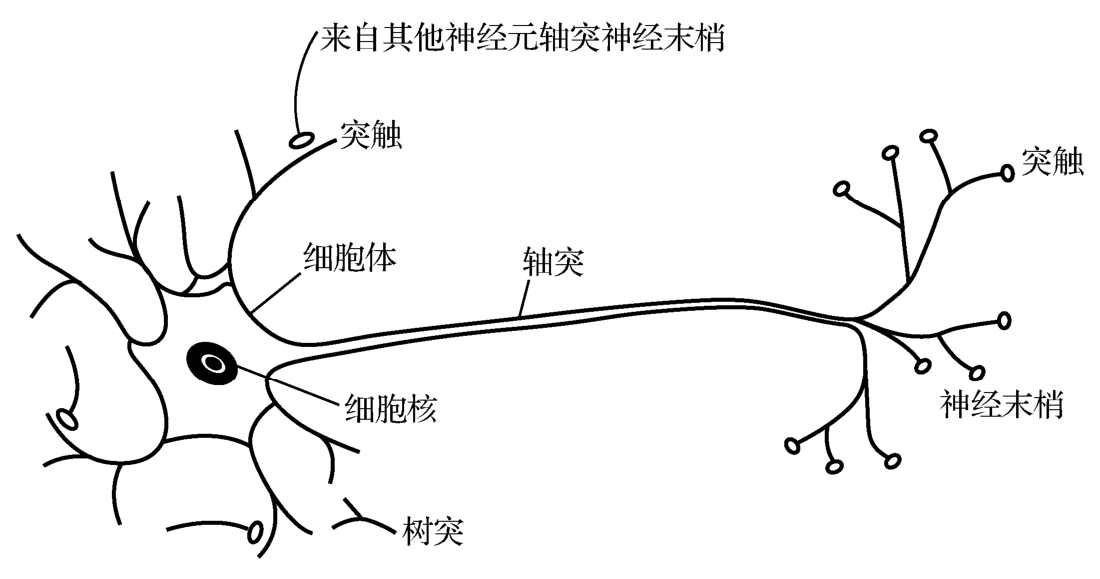
图1-4 生物神经元
生物神经元通过突触接收和传递信息。在突触的接收侧,信号被送入细胞体,这些信号在细胞体里被综合。其中有的信号起刺激作用,有的起抑制作用。当细胞体中接收的累加刺激超过一个阈值时,细胞体就被激发,此时它将通过枝蔓向其他神经元发出信号。
3.网络的拓扑结构
单个人工神经元的功能是简单的,只有通过一定的方式将大量的人工神经元广泛连接起来,组成庞大的人工神经网络,才能实现对复杂的信息进行处理和存储,并表现出不同的优越特性。根据神经元之间的连接的拓扑结构上的不同,将人工神经网络结构分为两大类,即层次型和互连型。
层次型神经网络将神经元按功能的不同分为若干层,一般有输入层、中间层(隐层)和输出层,各层顺序连接,如图1-5所示。输入层接收外部的信号,并由各输入单元传递给直接相连的中间层各个神经元。中间层是网络的内部处理单元层,它与外部没有直接连接。神经网络所具有的模式变换能力,如模式分类、模式完善、特征提取等,主要是在中间层进行的。根据处理功能的不同,中间层可以是一层的,也可以是多层的。由于中间层单元不直接与外部输入/输出进行信息交换,因此常将神经网络的中间层称为隐层,或隐含层、隐藏层等。输出层是网络输出运行结果并与显示设备或执行机构相连接的部分。
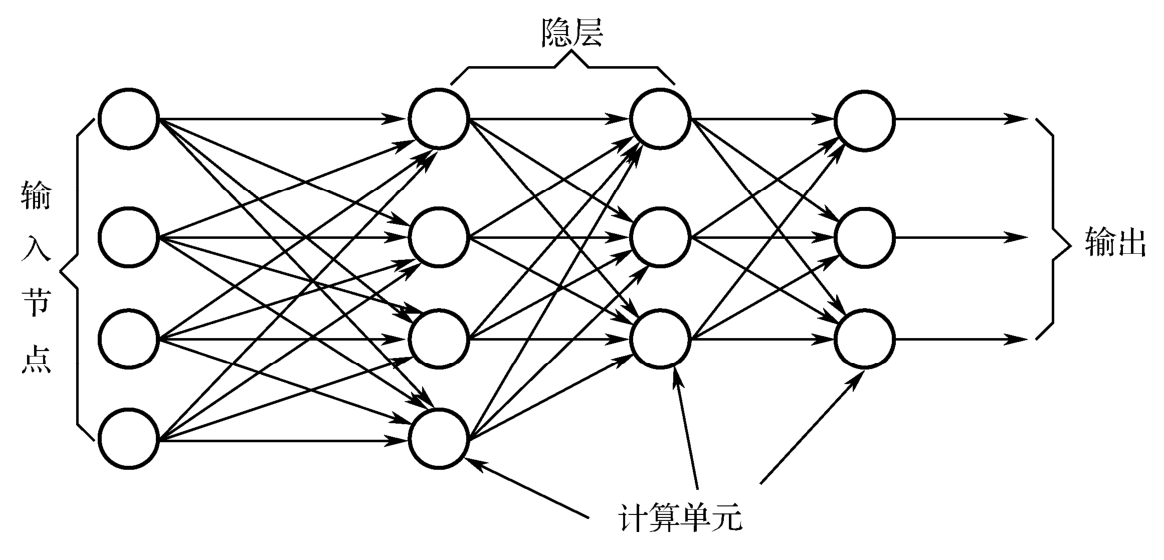
图1-5 层次型神经网络拓扑结构
互连型神经网络是指网络中任意两个神经元之间都是可以相互连接的,如图1-6所示。例如,Hopfield网络(循环网络)、波尔茨曼机模型网络的结构均属于这种类型。
4.网络的学习规则
神经网络的学习有两种形式:有导学习和无导学习。
有导学习又称监督学习(Supervised Learning)。一般情况下,有导学习的训练样本是输入/输出对(p i ,d i ),i=1,2,…,n,其中p i 为输入样本,d i 为输出样本(期望输出,或导师信号)。神经网络训练的目的是:通过调节各神经元的自由参数,使网络产生期望的行为,即当输入样本p i 时,网络输出尽可能接近d i 。
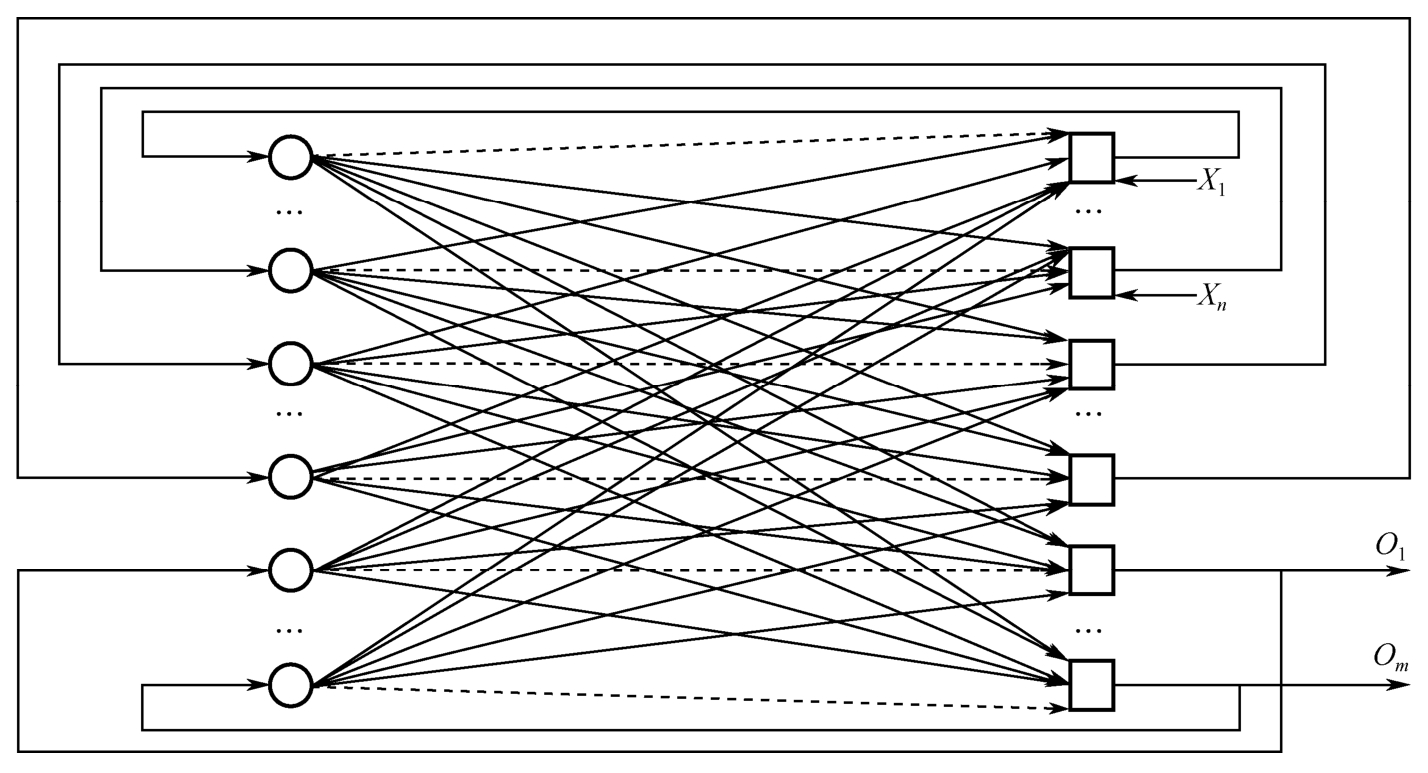
图1-6 全互连型神经网络拓扑结构
无导学习又称无监督学习(Unsupervised Learni ng)或自组织学习(Self-Organized Le arning)。无导学习不提供导师信号,只规定学习方式或某些规则,具体的学习内容随系统所处环境(输入信号情况)而异,系统可以自动发现环境特征和规律。
不管是有导学习还是无导学习,都要通过调整神经元的自由参数(权值或阈值)实现。
输入样本:x=(x 1 ,x 2 ,…,x n ,-1) T ;
当前权值:w(t)=(w 1 ,w 2 ,…,w n ,θ) T ;
期望输出:d=(d 1 ,d 2 ,…,d n ) T ;
权值调节公式:w(t+1)=w(t)+η·Δw(t),其中η为学习率,一般取较小的值,权值调整量Δw(t)一般与x、d及当前权值w(t)有关。
1)Hebb学习规则
输入样本:x=(x 1 ,x 2 ,…,x n ,-1) T ;
当前权值:w(t)=(w 1 ,w 2 ,…,w n ,θ) T ;
实际输出:y=f (w(t) T · x);
权值调节公式:w(t+1)=w(t)+η·Δw(t),其中权值调整量Δw(t)=y · x。
2)离散感知器学习规则
如果神经元的基函数取为线性函数,激活函数取为硬极限函数,则神经元就成了单神经元感知器,其学习规则称为离散感知器学习规则,是一种有导学习算法,常用于单层及多层离散感知器网络。
输入样本:x=(x 1 ,x 2 ,…,x n ) T ;
当前权值:w(t)=(w 1 ,w 2 ,…,w n ) T ;
期望输出:d=(d 1 ,d 2 ,…,d n ) T ;
当前输出:y=f (u)=sgn(w(t) T · x-θ);
当前误差信号:e(t)=d-y=d-sgn(w(t) T · x-θ);
当前权值调节量:Δw(t)=e(t) · x;
权值修正公式:w(t+1)=w(t)+η·Δw(t)。
3)δ(Delta)学习规则
1986年,认知心理学家Mc Clelland和Rume Chart在神经网络训练中引入了δ(Delta)学习规则,该规则又称连续感知器学习规则。
输入样本:x=(x 1 ,x 2 ,…,x n ) T ;
当前权值:w(t)=(w 1 ,w 2 ,…,w n ) T ;
期望输出:d=(d 1 ,d 2 ,…,d n ) T ;
基函数:
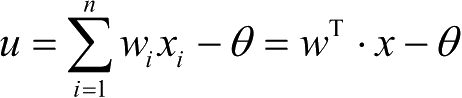 ;
;
实际输出:
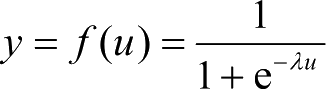 (激活函数);
(激活函数);
输出误差:
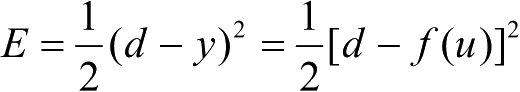 。
。
神经元权值调节δ学习规则的目的是:通过训练权值 w,使得对于训练样本对(x,d),神经元的输出误差
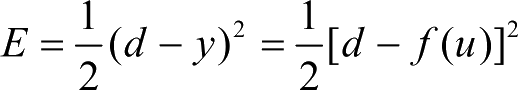 达到最小。误差E是权向量w的函数,欲使误差E最小,w应与误差的负梯度成正比,即Δw=-η·▽E,其中,比例系数η是一个常数,误差梯度▽E=(d-f (u)) · f′(u) · x。
达到最小。误差E是权向量w的函数,欲使误差E最小,w应与误差的负梯度成正比,即Δw=-η·▽E,其中,比例系数η是一个常数,误差梯度▽E=(d-f (u)) · f′(u) · x。
权值调整公式:w(t+1)=w(t)-η·[d-f (w T x)]· f (w T x)· x。
δ学习规则常用于单层、多层神经网络、BP网。
4)最小均方(LMS)学习规则
1962年,Bernard Widrow和Marcian Hoff提出了Widrow-Hoff学习规则,因为它能使神经元实际输出与期望输出之间的平方差最小,故又称最小均方(LMS)学习规则。
在δ学习规则中,若激活函数 f(·)取:y=f (w T x)=w T x,则δ学习规则就成为LMS学习规则。
输入样本:x=(x 1 ,x 2 ,…,x n ) T ;
当前权值:w(t)=(w 1 ,w 2 ,…,w n ) T ;
期望输出:d=(d 1 ,d 2 ,…,d n ) T ;
基函数:
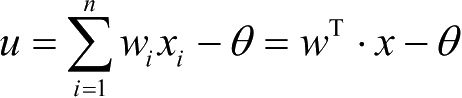 ;
;
实际输出:y=f (u)=w T x (激活函数);
输出误差:
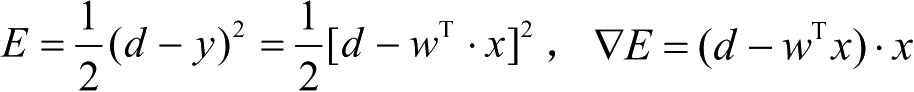 ;
;
权值调整公式:w(t+1)=w(t)-η· (d-w T ) · x。
最小均方学习规则常用于自适应线性单元。
5)竞争学习规则
竞争学习规则又称Winner-Take-All(胜者为王)学习规则,用于无导师学习。一般将网络的某一层确定为竞争层,对于一个特定的输入 x,竞争层的所有神经元均有输出响应,其中响应值最大的神经元 m 为在竞争中获胜的神经元,即
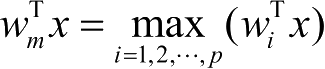 。只有获胜神经元才有权调整其权向量 w
m
,调整量Δw
m
=α· (x-w
m
),α∈(0,1]。它是学习常数,一般其值随着学习进展的增大而减少。两个向量的点积越大,表明两者越近似,所以调整获胜的神经元权值使w
m
进一步接近当前输入 x。显然,当下次出现与 x 相像的输入模式时,上次获胜的神经元更容易获胜,在反复的竞争学习过程中,竞争层的各神经元所对应的权向量被逐渐调整为样本空间的聚类中心。
。只有获胜神经元才有权调整其权向量 w
m
,调整量Δw
m
=α· (x-w
m
),α∈(0,1]。它是学习常数,一般其值随着学习进展的增大而减少。两个向量的点积越大,表明两者越近似,所以调整获胜的神经元权值使w
m
进一步接近当前输入 x。显然,当下次出现与 x 相像的输入模式时,上次获胜的神经元更容易获胜,在反复的竞争学习过程中,竞争层的各神经元所对应的权向量被逐渐调整为样本空间的聚类中心。
在智能工厂设备应用中,粒子群(PSO)算法在函数优化、神经网络训练、调度问题、故障诊断、建模分析、电力系统优化设计、模式识别、图像处理、数据挖掘等众多领域中均有相关的研究应用报道,取得了良好的实际应用效果。
1.粒子群算法基本原理
粒子群算法最原始的工作可以追溯到1987年Reynolds对鸟群社会系统Boids (Reynolds对其仿真鸟群系统的命名)系统的仿真研究,在鸟类仿真中,Boids系统采取了下面三条简单的规则。
(1)飞离最近的个体(鸟),避免与其发生碰撞冲突。
(2)尽量使自己与周围的鸟保持速度一致。
(3)尽量试图向自己认为的群体中心靠近。
虽然只有三条规则,但 Boids 系统已经表现出非常逼真的群体聚集行为。但Reynolds仅仅实现了该仿真,并无实用价值。
1995年,Kenned和Eberhart在Reynolds等人的研究基础上,创造性地提出了粒子群优化算法,即在 Boids 系统中加入了一个特定点—定义为食物,每只鸟根据周围鸟的觅食行为来搜寻食物,其初衷是希望模拟研究鸟群觅食行为,但实验结果却显示这个仿真模型蕴含着很强的优化能力,尤其是在多维空间中的寻优。最初仿真时,每只鸟在计算机屏幕上显示为一个点,而“点”在数学领域具有多种意义,于是用“粒子(particle)”来称呼每个个体,这样就产生了基本的粒子群算法。
假设在一个D维搜索空间中,有m个粒子组成一粒子群,其中第i个粒子的空间位置为X i =(x i1 ,x i2 ,x i3 ,…,x id ),i=1,2,…,m,它是优化问题的一个潜在解,将它代入优化目标函数可以计算出其相应的适应值,根据适应值可衡量x i 的优劣;第 i 个粒子所经历的最好位置称为其个体历史最好位置,记为P i =(p i1 ,p i2 ,p i3 ,…,p id ),i=1,2,…,m,相应的适应值为个体最好适应值F i ;同时,每个粒子还具有各自的飞行速度V i =(v i1 ,v i2 ,v i3 ,…,v iD ),i=1,2,…,m。在所有粒子经历过的位置中,最好的位置称为全局历史最好位置,记为p g =(p g1 ,p g2 ,p g3 ,…,p gd ),相应的适应值为全局历史最优适应值。
在基本PSO算法中,对于第n代粒子,其第d维(1≤d≤D)元素的速度、位置更新公式为
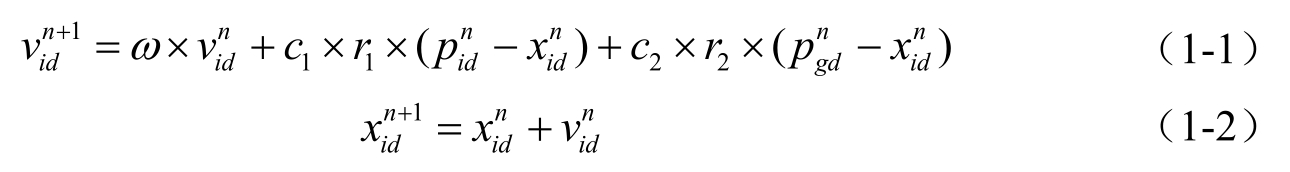
式中,ω为惯性权值;c 1 和c 2 都为正常数,称为加速系数;r 1 和r 2 是两个在[0,1]范围内变化的随机数。
第d维粒子元素的位置变化范围和速度变化范围分别限制为[X d,min ,X d,max ]和[V d,min ,V d,max ]。迭代过程中,若某1维粒子元素的X id 或V id 超出边界值则令其等于边界值。
式(1-1)中的第 1 部分
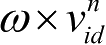 由粒子先前速度的惯性引起,为“惯性”部分;第 2 部分
由粒子先前速度的惯性引起,为“惯性”部分;第 2 部分
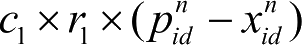 为“认知”部分,表示粒子本身的思考,即粒子根据自身历史经验信息对自己下一步行为的影响;第3部分
为“认知”部分,表示粒子本身的思考,即粒子根据自身历史经验信息对自己下一步行为的影响;第3部分
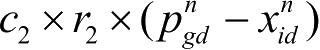 为“社会”部分,表示粒子之间的信息共享和相互合作,即群体信息对粒子下一步行为的影响。
为“社会”部分,表示粒子之间的信息共享和相互合作,即群体信息对粒子下一步行为的影响。
2.基本PSO算法
基本PSO算法步骤如下。
(1)粒子群初始化。
(2)根据目标函数计算各粒子适应度值,并初始化个体、全局最优值。
(3)判断是否满足终止条件,是则搜索停止,输出搜索结果;否则继续下步。(4)根据速度、位置更新公式更新各粒子的速度和位置。
(5)根据目标函数计算各粒子适应度值。
(6)更新各粒子历史最优值及全局最优值。
(7)跳转至步骤(3)。
对于终止条件,通常可以设置为适应值误差达到预设要求,或迭代次数超过最大允许迭代次数。
这里以寻找函数y=1-cos(3x)·exp(-x)在[0,4]的最大值为例,该函数图形如图1-7所示。
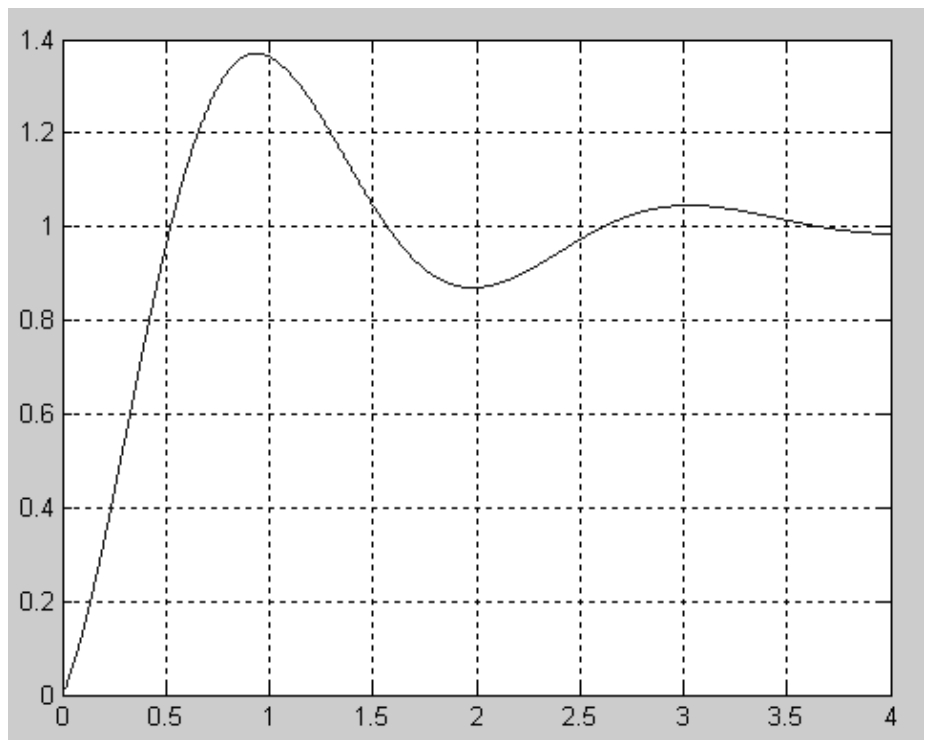
图1-7 函数图形
为了得到该函数的最大值,可以在[0,4]之间随机取一些点。为了演示,放置两个点,并且计算这两个点的函数值,同时给这两个点设置在[0,4]之间的一个速度。这些点就会按照一定的公式更改自己的位置,到达新位置后,再计算这两个点的值,然后再按照一定的公式更新自己的位置。直到最后在y=1.3706这个点停止自己的更新。这个过程与粒子群算法作为对照如下:这两个点就是粒子群算法中的粒子,该函数的最大值就是鸟群中的食物,计算的两个点的函数值就是粒子群算法中的适应值,计算用的函数就是粒子群算法中的适应度函数。图 1-8 所示求最大值时采用基本PSO算法过程的变化情况,分别表示第1次初始化、第1次更新位置、第2次更新位置、第21次更新位置和最后的结果(30次迭代),最后所有的点都集中在最大值的地方。
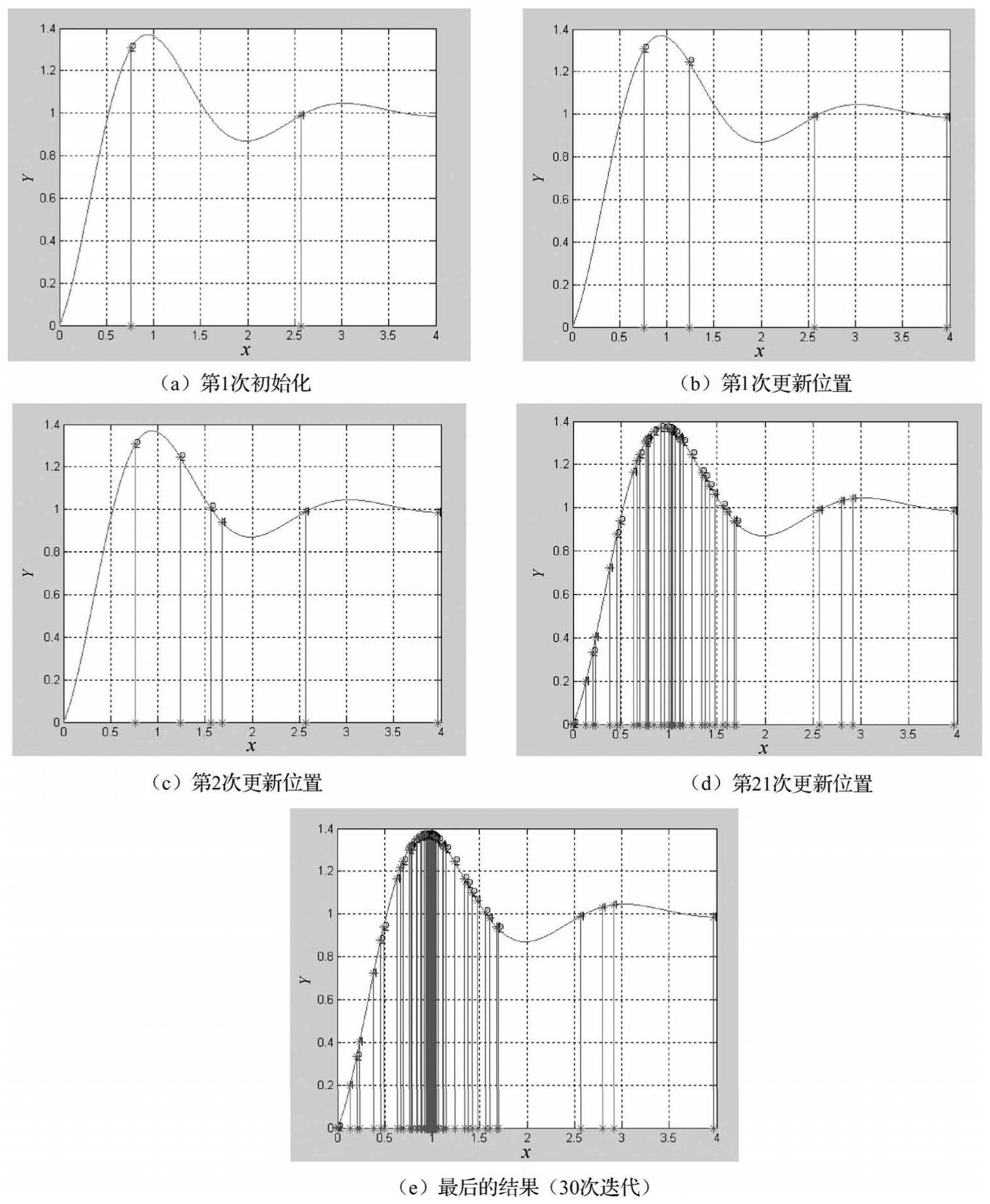
图1-8 采用基本PSO算法过程的变化情况
基本连续PSO算法中,其主要参数(惯性权值、加速系数、种群规模和迭代次数)对算法的性能均有不同程度的影响。
惯性权值ω的取值对基本PSO算法的收敛性能至关重要。在最初的基本粒子群算法中没有惯性权值这一参数。最初的基本PSO算法容易陷入局部最小,于是在其后的研究中引入了惯性权值来改善基本PSO算法的局部搜索能力,形成了目前常用的基本PSO算法形式。取较大的ω值使得粒子能更好地保留速度,从而能更快地搜索解空间,提高算法的收敛速度;但同时由于速度大可能导致算法无法更好地进行局部搜索,容易错过最优解,特别是过大的ω会使得基本PSO算法速度过大而无法搜索到全局最优。取较小的ω值则有利于局部搜索,能够更好地搜索到最优值,但因为粒子速度受其影响相应变小,从而无法更快地进行全局搜索,进而影响算法收敛速度;同时,过小ω值更容易导致算法陷入局部极值。因此,一个合适的ω值能有效兼顾搜索精度和搜索速度、全局搜索和局部搜索,保证算法性能。
加速系数c 1 和c 2 代表每个粒子向其个体历史最好位置和群体全局历史最好位置的移动加速项的权值。较低的加速系数值可以使得粒子收敛到其最优解的过程较慢,从而能够更好地搜索当前位置与最优解之间的解空间;但过低的加速系数值可能导致粒子始终徘徊在最优邻域外而无法有效搜索目标区域,从而导致算法性能下降。较高的加速系数值则可以使得粒子快速集中于目标区域进行搜索,提高算法效率;但过高的加速系数值有可能导致粒子搜索间隔过大,容易越过目标区域而无法有效地找到全局最优解。因此,加速系数对基本PSO算法能否收敛也起到重要作用,合适的加速系数有利于算法较快地收敛,同时具有一定的跳出局部最优的能力。
式(1-1)中,若 c 1 =c 2 =0,粒子将一直以当前的速度进行惯性飞行,直到到达边界。此时粒子仅仅依靠惯性移动,不能从自己的搜索经验和其他粒子的搜索经验中吸取有用的信息,因此无法利用群体智能,基本PSO算法没有启发性,粒子只能搜索有限的区域,很难找到全局最优解,算法优化性能很差。若c 1 =0,则粒子没有认知能力,不能从自己的飞行经验中吸取有效信息,只有社会部分,所以c又称社会参数;此时收敛速度比基本PSO算法速度快,但由于不能有效利用自身的经验知识,所有的粒子都向当前全局最优集中,因此无法很好地对整个解空间进行搜索,在求解存在多个局部最优的复杂优化问题时比基本PSO算法容易陷入局部极值,优化性能也变差。若c 2 =0,则微粒之间没有社会信息共享,不能从同伴的飞行经验中吸取有效信息,只有认知部分,所以c又称认知参数;此时个体间没有信息共享,一个规模为m的粒子群等价于m个单个粒子的运行,搜索到全局最优解的概率很小。
在基本PSO算法中,群体规模对算法的优化性能也影响很大。一般来说,群体规模越大,搜索到全局最优解的可能性也越大,优化性能相对也越好;但同时算法消耗的计算量也越大,计算性能相对下降。群体规模越小,搜索到全局最优解的可能性就越小,但算法消耗的计算量也越小。群体规模对算法性能的影响并不是简单的线性关系,当群体规模达到一定程度后,再增加群体规模对算法性能的提升是有限的,反而增加了运算量;但群体规模不能过小,过小的群体规模将无法体现出群体智能优化算法的智能性,导致算法性能严重受损。
较大的迭代次数使得算法能够更好地搜索解空间,因此找到全局最优解的可能性也大些;相应的,较小的最大允许迭代次数会减小算法找到全局最优解的可能性。对于基本连续PSO算法来说,由于缺乏有效的跳出局部最优操作,因此粒子一旦陷入局部极值后就难以跳出,位置更新处于停滞状态,此时迭代次数再增多也无法提高优化效果,只会浪费计算资源。但过小的迭代次数会导致算法在没有对目标区域实现有效搜索之前就停止更新,将严重影响算法性能。此外,随机数可以保证粒子群群体的多样性和搜索的随机性。最大、最小速度可以决定当前位置与最好位置之间区域的分辨率(或精度)。如果最大速度(或最小速度)的绝对值过大,粒子可能会因为累积的惯性速度太大而越过目标区域,从而无法有效搜索到全局最优解;但如果最大速度(或最小速度)的绝对值过小,则粒子不能迅速向当前全局最优解集中,对其邻域进行有效的搜索,同时还容易导致局部极值无法跳出的问题。
因此,最大、最小速度的限制主要是为了防止算法计算溢出、改善搜索效率和提高搜索精度。基本PSO 算法中只涉及基本的加、减、乘运算操作,编程简单,易于实现,关键参数较少,设定相对简单,所以引起了广泛的关注。
3.离散二进制PSO算法
为了解决离散优化问题,Kennedy和Eberhart于1997年在基本PSO算法的基础上提出了一种离散二进制PSO(KBPSO)算法。在KBPSO算法中,粒子定义为一组由(0,1)组成的二进制向量。KBPSO算法保留了原始的连续PSO算法的速度公式,即式(1-1),但速度丧失了原始的物理意义。在KBPSO算法中,速度值 v id 通过预先设计的 S 形限幅转换函数Sig(v id )转换为粒子元素x id 取“1”的概率。速度值v id 越大,则粒子元素位置x id 取1的可能性越大,反之则越小。

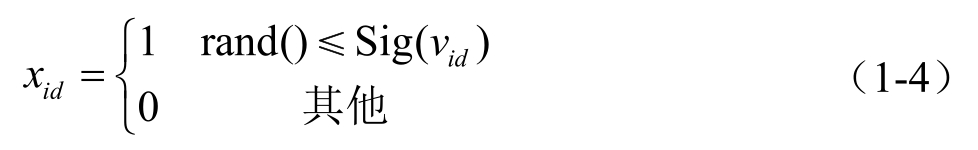
其中,Sig(v id )为Sigmoid函数,通常为防止速度过大,令v id ∈[v id min ,v id max ],以使概率值不会过于接近 0 或 1,保证算法能以一定的概率从一种状态跃迁到另一种状态,防止算法早熟。
基于基本连续 PSO 算法的信息机制,Shen 等人提出了一种改进的离散二进制粒子群算法(SBPSO),用于QSAR(Quantitative Structure—activity Relationship)建模的特征选择中。SBPSO 算法中舍弃了基本 PSO 算法中的速度、位置更新公式,重新定义速度v i 为一个在0到1之间的随机数,粒子元素的位置x id 则根据下列规则由随机产生的v id 确定
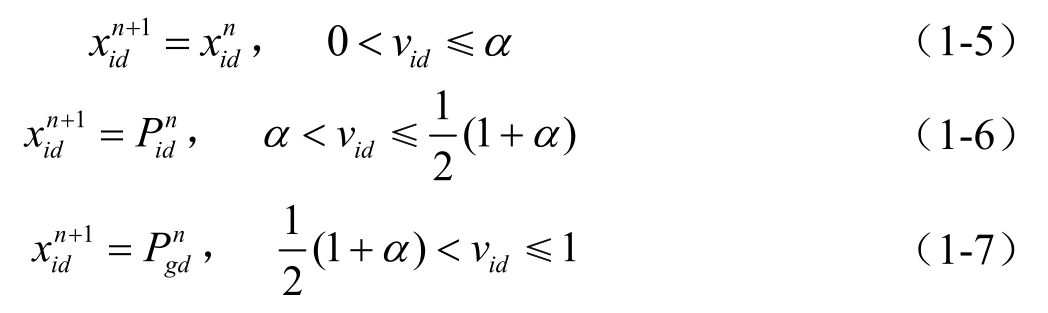
其中,α∈(0,1)称为静态概率(static probability),是SBPSO 算法中唯一的可调参数,它可以是一个常数、一个变量或一个随机数。
虽然SBPSO算法的更新公式在形式上与KBPSO算法及基本PSO算法都有很大的改变,但其基本的思想不变,即每个粒子都只与自身历史最优值和全局最优值进行信息交流,BPSO算法位置更新公式,即式(1-5),类似于基本连续PSO算法速度更新公式中的第一项,都是一种“惯性”的表现,只不过SBPSO算法是停留在原来的位置,而基本PSO算法中是根据速度惯性继续搜索。同样,SBPSO算法位置更新公式,即式(1-6)、式(1-7)则分别对应了基本PSO算法速度更新公式中的第二、三项,分别代表了粒子的“认知”部分和“社会”部分,表示粒子自身和社会群体对粒子下一步行为的影响。式(1-5)增强了SBPSO算法的全局搜索能力,使得粒子能够有效地对目标区域进行搜索,找出全局最优解。没有式(1-5),粒子将完全跟随自己的两个最优解“飞行”,从而容易陷入局部最优值。式(1-6)、式(1-7)则根据先前的搜索经验对粒子搜索进行指导,没有这两项,SBPSO 算法则变成了完全的随机搜索。因此,在SBPSO算法中,静态概率α替代了基本PSO算法中的ω、c 1 、c 2 等参数,对算法的性能至关重要。较大的α能使得算法更好地搜索解空间,从而能够更好地跳出局部最优搜索到全局最优;但过大的α会导致算法无法充分利用已有的寻优信息,致使算法收敛速度过慢。较小的α可以使得粒子快速集中于最优邻域,提高收敛速度,但容易导致算法陷入局部最优。