




矢量代数又称为计算几何,是计算理论科学的一个重要分支。该学科自20世纪70年代末从算法设计与分析中独立出来,近些年已经有了巨大的发展,不仅产生了一系列重要的理论成果,也在众多实际领域中得到了广泛的应用。一般定义的矢量称为自由矢量,物理学中应用的某些矢量有时还具有一些附加的特征,这类矢量称为约束矢量,包括定位矢量和滑动矢量。定位矢量是指矢量的作用点为一确定位置;滑动矢量是指矢量的作用点可以沿矢量的作用线自由滑动。若对于标量 t 的每一个数值,都有变矢量θ的确定量(大小方向都确定的矢量)与之相对应,则变矢量θ称为自变量 t 的矢量函数,记作 θ = θ ( t )。矢量函数还可表示为 θ = xi + yj + zk ,其中, x = x ( t ), y = y ( t ), z = z ( t )为3个标量函数。
若把坐标系中任一点
M
所在位置的变矢量
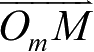 表示成径矢形式
a
,则当
t
变动时,点
M
在空间描绘出一条曲线,称为矢量函数的矢端曲线。类似于标量函数的数学分析,可引入矢量函数的极限、连续、导数、微分、不定积分和定积分等概念。为了避免不必要的重复,这里仅着重叙述矢量函数导数的定义。
表示成径矢形式
a
,则当
t
变动时,点
M
在空间描绘出一条曲线,称为矢量函数的矢端曲线。类似于标量函数的数学分析,可引入矢量函数的极限、连续、导数、微分、不定积分和定积分等概念。为了避免不必要的重复,这里仅着重叙述矢量函数导数的定义。
如图1-1中三维空间内的位置可以用矢量形式表示
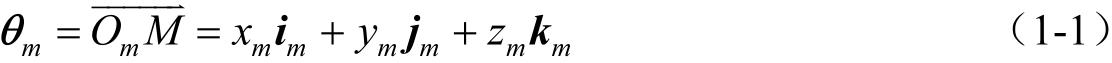
式中,( i m , j m , k m )是坐标轴的单位矢量,或者用列矩阵表示

式中,下角标“ m ”指明,位置矢量表示在坐标系 S m ( x m , y m , z m )中。在标记矢量时,可以采用行矩阵表示位置矢量。

式(1-3)中,
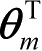 是关于
是关于
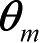 的转置矩阵。
的转置矩阵。
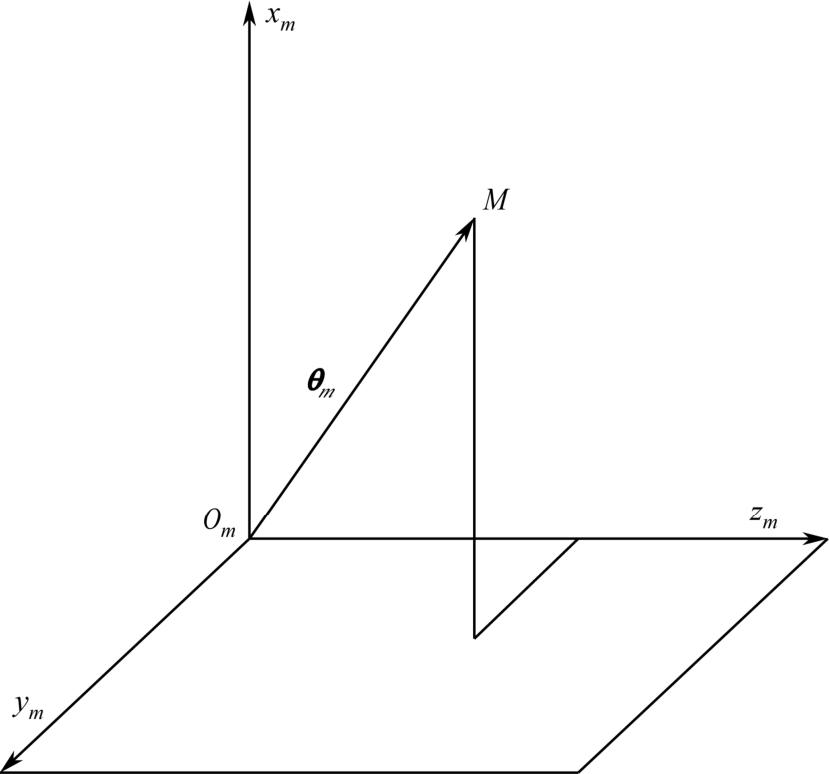
图1-1 在笛卡尔坐标系中的位置矢量
在笛卡尔坐标系中一般采用3个数( x , y , z )来确定位置矢量的顶点。通常,坐标变换需要使用矩阵的乘法和加法混合运算的方法。然而,如果位置矢量用齐次坐标表示,则只需要矩阵的乘法。在三维立体空间中,一个点的齐次坐标由4个数( x ∗ , y ∗ , z ∗ , t ∗ )来确定,这4个数不同时为零,并且其中只有3个数是独立数。假定 t ∗ ≠0,则普通坐标和齐次坐标之间的关系式为

利用 t * =1,则一个点可以用齐次坐标表示为( x , y , z ,1),而一个位置矢量可以用矩阵表示为

矢量函数的极限和连续性与标量函数类似,其导数形式也与标量函数类似。对于矢量函数
θ
=
θ
(
t
)和
t
0
∈(
t
1
,
t
2
)若存在极限,则极限就称作
θ
=
θ
(
t
)在
t
0
处的导矢,记作
θ
′(
t
0
)或
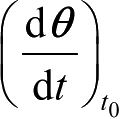 。
。
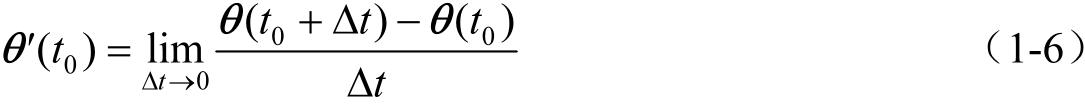
如果将矢量函数 θ = θ ( t )用3个分量来表示,即

则它们作为普通的标量函数,众所周知,关于标量函数数学分析中的种种概念对于各个分量也同样适用。利用数量分析理论,结合基本矢,对各个分量稍加处理,即可成为矢量分析的相应内容。如导矢

式中,
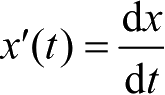 ,
,
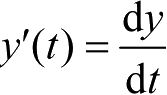 ,
,
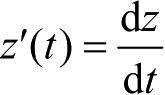 。
。
若 θ ( t )的矢端轨迹为一条曲线,则Δ θ 是该曲线上参数分别为 t 0 和 t 0 +Δ t 的两点所引的弦上矢量。显然当Δ t 为正值时,Δ θ /Δ t 与Δ θ 同向,反之为异向。为了方便,统一把有向曲线 t 增加的方向作为正向,则当Δ t →0时,Δ θ /Δ t 的极限显然就是 t 0 处切线方向的矢量,并且总是指向曲线的正向,如图1-2所示。
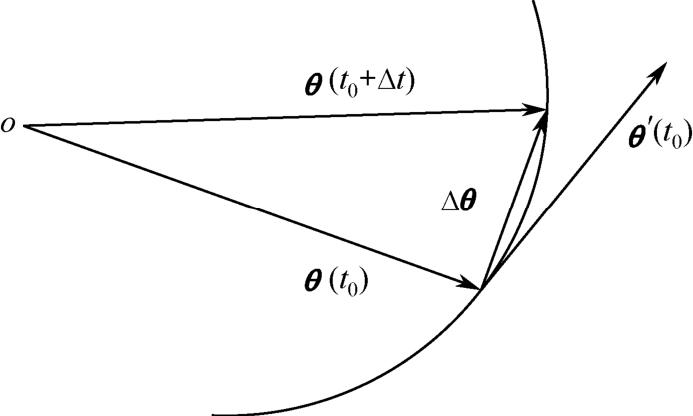
图1-2 曲线的切线矢量
矢量函数微分的定义和形式与标量函数类似。对于复合函数

则有

矢量函数的泰勒公式如下:
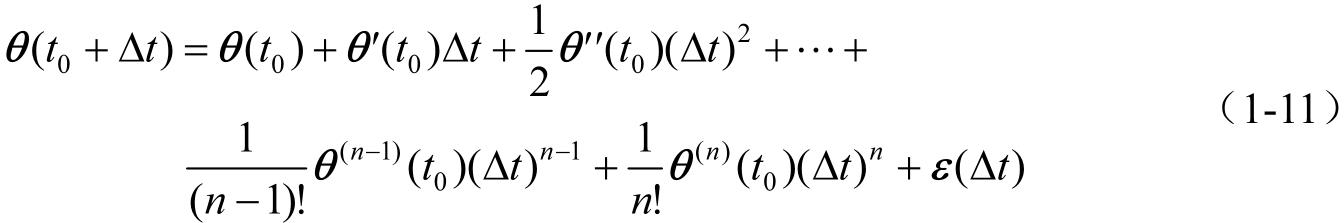
式中,ε为无穷小矢量,
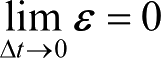 。
。
矢量函数 θ ( t )的不定积分为

式中, ψ ( t )为 θ ( t )的一个原函数,即 ψ ′( t )= θ ( t ), C 为常矢。
若矢量函数 θ ( t )= x ( t ) i + y ( t ) j + z ( t ) k 是可积的,则有
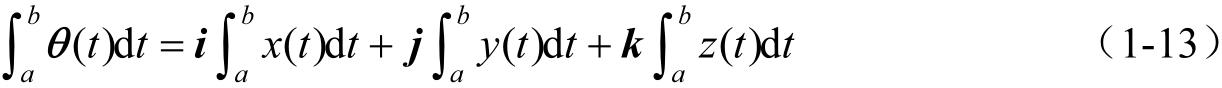
标量函数定积分的概念以及定积分的许多性质都可以相应地推广到矢量函数中,其基本公式仍然是

式中, ψ ( t )为 θ ( t )的任一原函数。
1.直线矢量方程
这里先讲解一下直线矢量方程,直线矢量方程的概念在本书参考文献里可以找到。直线可以用坐标函数方程表示,也可以用矢量方程表示,如图1-3所示, l 为空间任意直线, 0 P 为 l 上的已知点,其径矢为 θ 0 , v 为与 l 平行的不等于零的矢量。若 θ 为直线 l 上的任意点 P 的径矢,则直线 l 的参数方程为
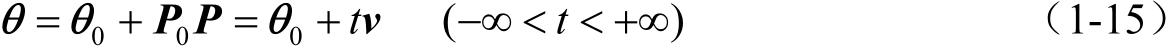
若 P 1 为直线上另一已知点,其径矢为 θ 1 ,令上式中的 v = θ 1 − θ 0 ,则直线 l 的参数方程又可以写为
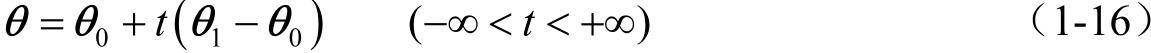
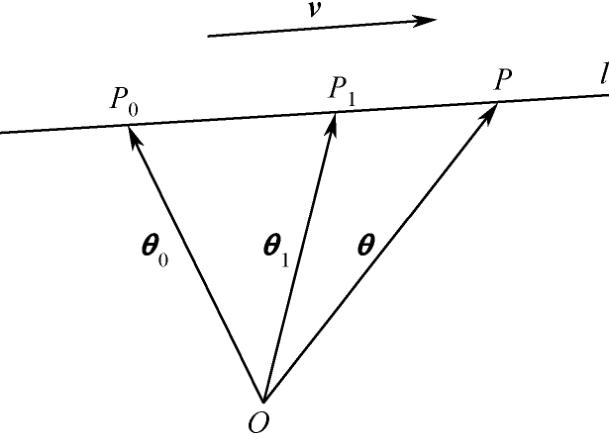
图1-3 直线矢量
2.平面矢量方程
如图1-4所示, P 0 为 π 平面上的已知点,其径矢为 θ 0 , n 为与 π 平面垂直的不等于零的矢量。若 θ 为 π 平面上任意点的径矢,则 P 0 P = θ − θ 0 ,且与 n 相垂直,故 π 平面的矢量方程为

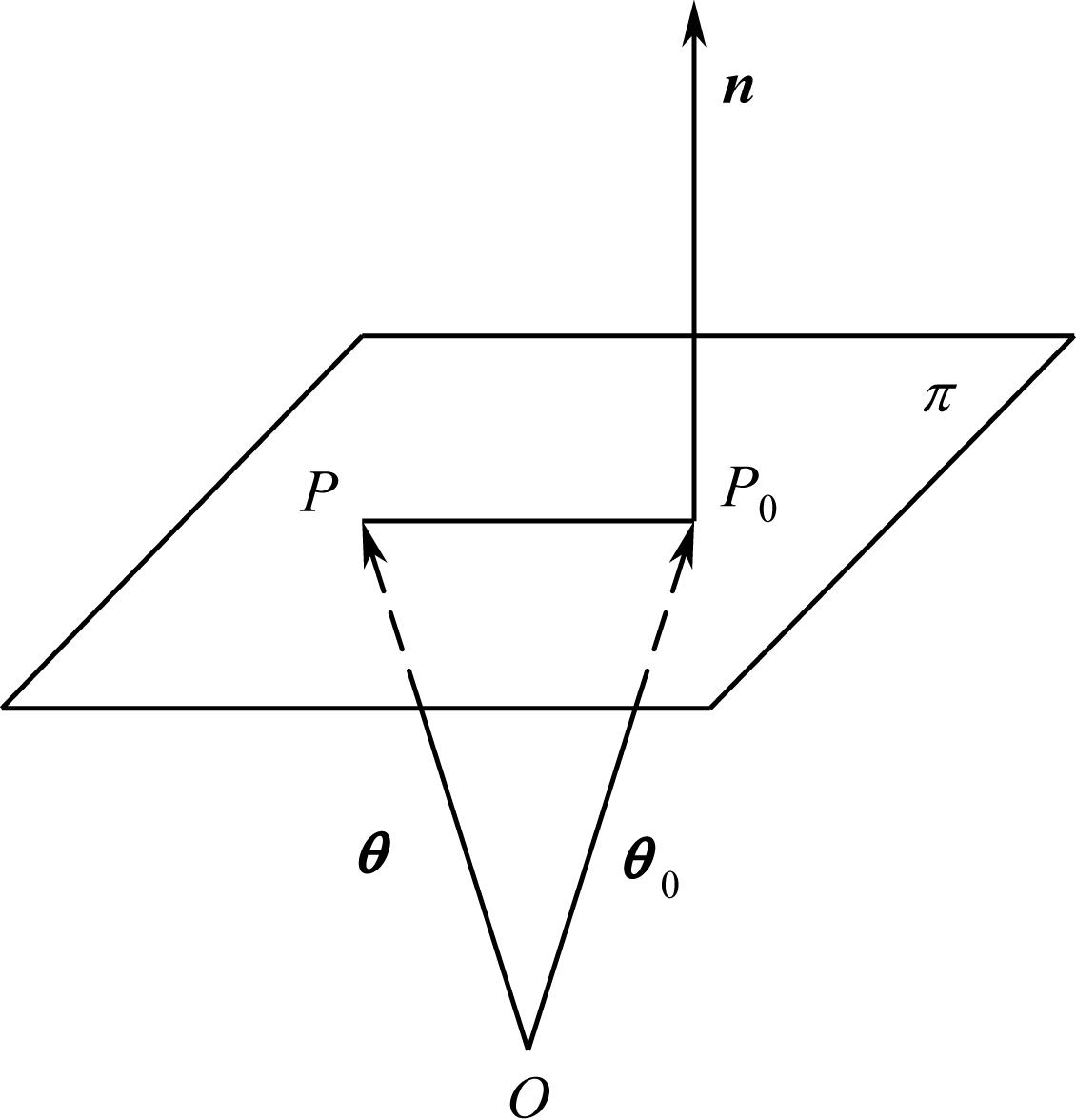
图1-4 垂直矢量之间的关系
若 v 1 、 v 2 为平行于 π 平面、彼此不平行的两个矢量。由于 P 0 P = θ − θ 0 与( v 1 × v 2 )相垂直,如图1-5所示,则 π 平面的矢量方程可写成

若 P 1 、 P 2 为 π 平面上不与 P 0 共线的两点,它们的径矢分别为 θ 1 、 θ 2 ,由于( θ − θ 0 )、( θ 1 − θ 0 )、( θ 2 − θ 0 )为 π 平面上三个不平行的矢量,如图1-6所示, π 平面的矢量方程又可写为
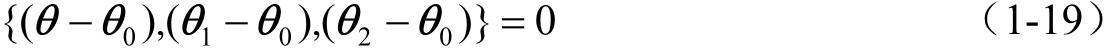
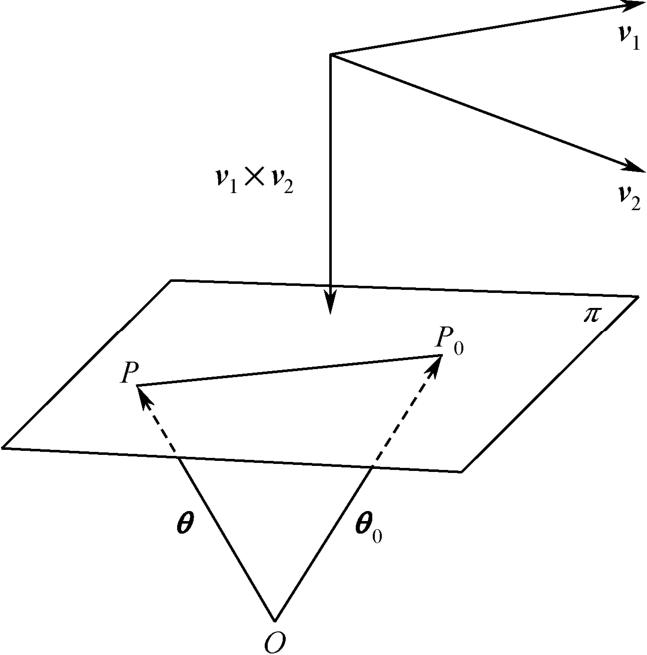
图1-5 两个不平行矢量之间的关系
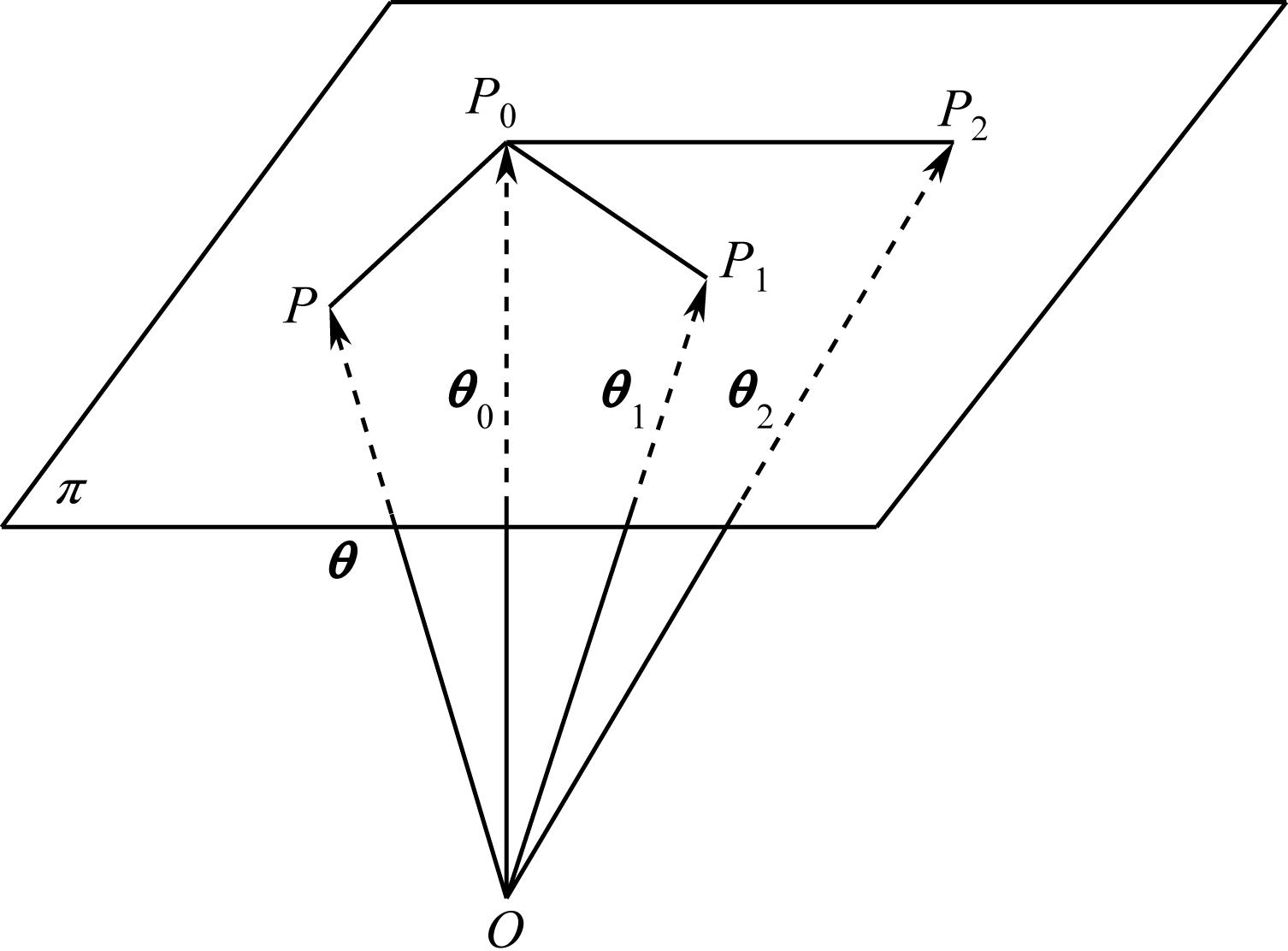
图1-6 三个不平行矢量之间的关系