




为了说明质点的位置、运动的快慢、方向等,必须为其选取坐标系。在参照系中,为确定空间一点的位置,按规定方法选取的有次序的一组数据,就叫作“坐标”。在某一问题中规定坐标的方法,就称为坐标系。坐标系分为以下几种:笛卡尔直角坐标系、平面极坐标系、柱坐标系和球坐标系等。直角坐标系还可称为正交坐标系。
选择坐标系对于研究交错传动两齿面间的共轭关系以及几何参数间的内在联系是极其重要的。坐标系的选择是否合理,不仅会对所得公式的形式造成影响,而且运算的繁简程度也会有所不同。因此,合理选择坐标系是研究空间啮合原理的重要基础,一般情况下多采用四坐标系,蜗杆与蜗轮啮合的四坐标系如图1-7所示。三维空间中的相互啮合,显然应该采用三维坐标系。
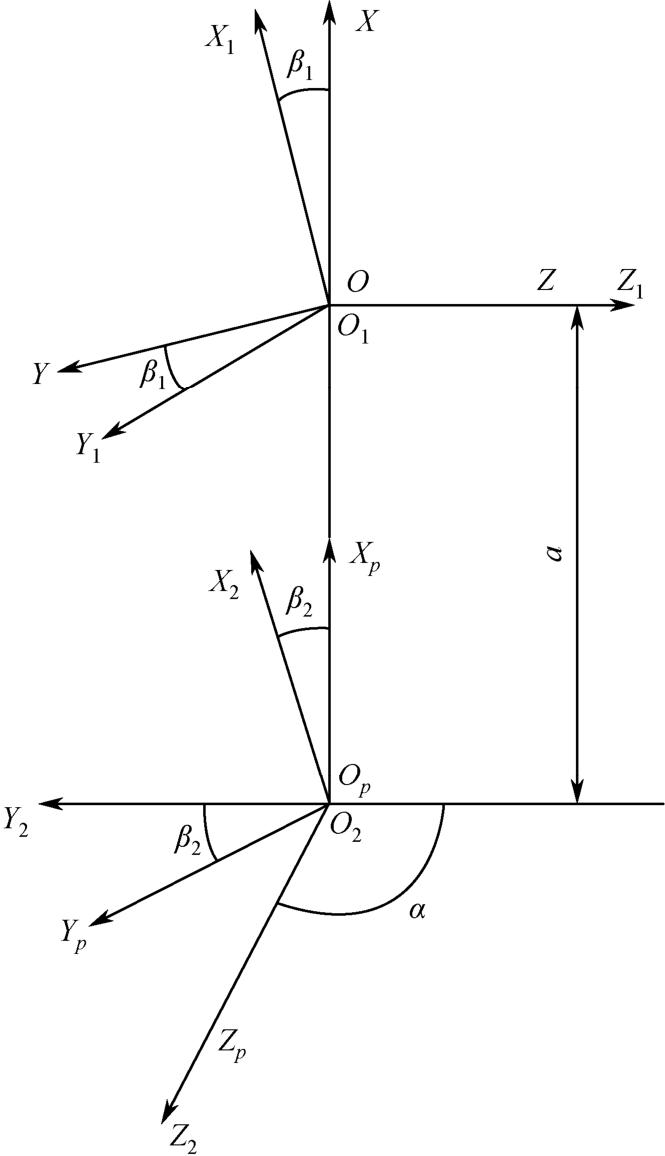
图1-7 蜗杆与蜗轮啮合的四坐标系
动坐标系 S 1 ( O 1 X 1 Y 1 Z 1 )与蜗杆1相固连,其中 Z 1 轴与蜗杆回转轴重合;动坐标系 S 2 ( O 2 X 2 Y 2 Z 2 )与蜗轮2相固连,其中 Z 2 轴与蜗轮的回传轴重合。以 Z 1 、 Z 2 轴的垂足 O 1 、 O 2 作为坐标系 S 1 和 S 2 的原点,并以其公垂线作为 X 1 、 X 2 轴的起始位置。 Y 1 和 Y 2 轴的方向按右手定则来确定。
在固定坐标系 S ( OXYZ )中,原点 O 与 O 1 重合, Z 轴与 Z 1 轴重合, X 轴与公垂线 O 2 O 1 重合。
辅助坐标系 S p ( O p X p Y p Z p )的建立是为了便于进行坐标系变换,其坐标原点 O p 与 O 2 重合, X p 与 X 轴重合, Z p 与 Z 2 轴重合。
Z
1
、
Z
2
两轴间的垂直距离即蜗杆与蜗轮的中心距
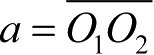 ;而夹角
α
为蜗杆与蜗轮轴线间的交错角。
;而夹角
α
为蜗杆与蜗轮轴线间的交错角。
坐标变换是空间实体的位置描述,通过建立两个坐标系统之间一一对应的关系来实现,是从一种坐标系统到另一种坐标系统的变换过程。分析空间啮合一般都在同一坐标系内,因此需要多次对坐标轴移动与坐标原点移动的坐标变换公式进行推导。为了确保坐标变换公式的条理化和正确性,现用矩阵作为坐标变换的算子,坐标变换的公式通过算符的形式来表示。
例如,要求图1-7中从坐标系 S 至坐标系 S p 的变换关系。可将坐标系 S 沿 X 轴的负方向移动距离 a ,使 S 的原点与 S p 的原点重合;若再将 S 绕 X 轴回转 α 角,则 S 与 S p 将完全重合。坐标系 S 与 S p 各坐标轴间的方向余弦及原点位置间的关系如表1-1所示。
表1-1 坐标系 S 与 S p 各坐标轴间的方向余弦及原点位置间的关系
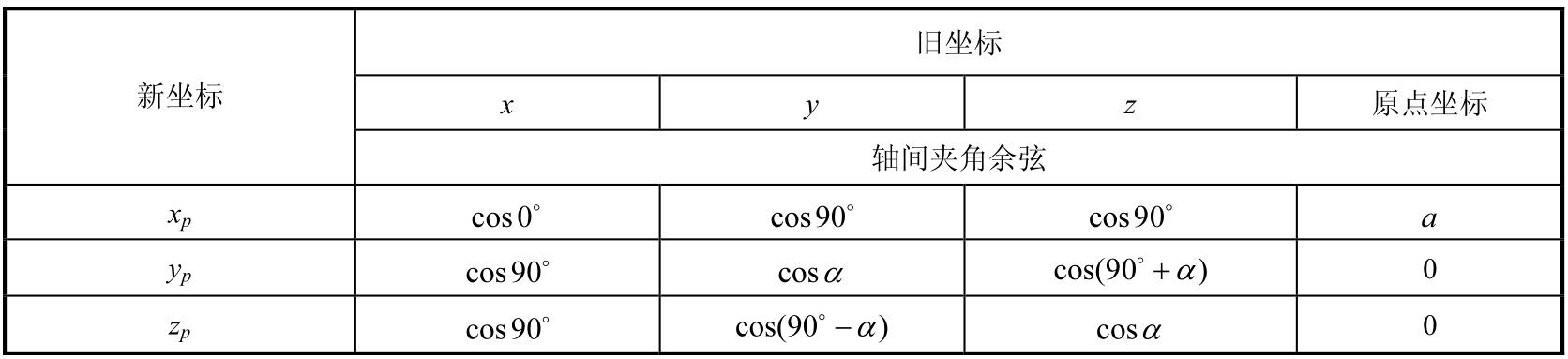
各坐标间的关系式可表示为

系数矩阵为
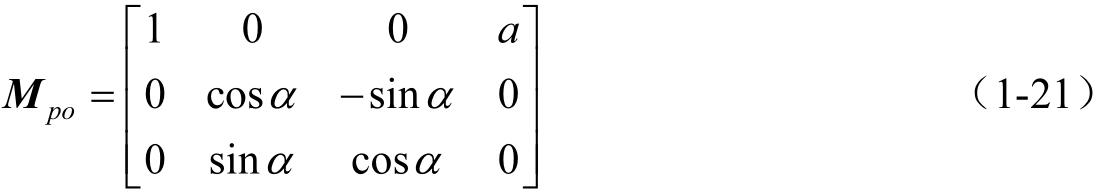
为了使式(1-20)能写成两矩阵乘积的形式,根据矩阵相乘的法则,只有当前一矩阵的列数等于后一矩阵的行数时,两矩阵才能相乘。为此,在式中添加一恒等式 t p = t =1,则式(1-20)变为
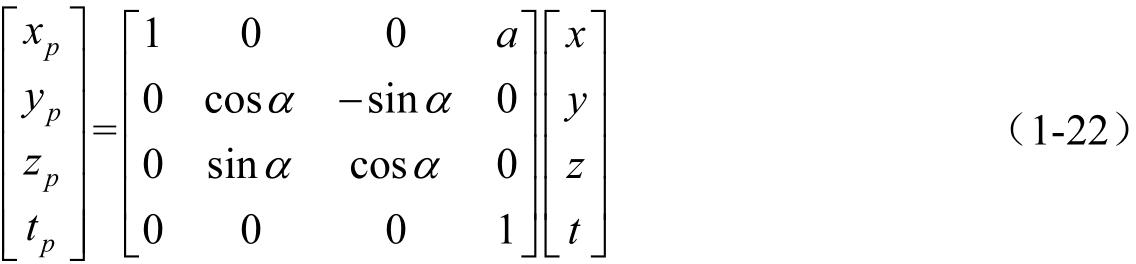
由坐标系 S 变换到坐标系 S p 的系数矩阵为
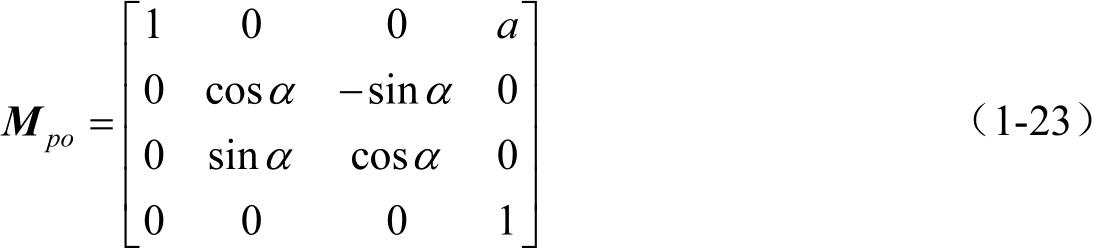
这样,由坐标系 S 变换到坐标系 S p 的坐标变换公式为

用矢量表示为

式中, r p 、 r 为空间一点在坐标系 S p 、 S 的径矢。
同理,坐标系 S p 与 S 中各坐标轴间的方向余弦及坐标原点间的关系如表1-2所示。
表1-2 坐标系 S p 与 S 中各坐标轴间的方向余弦及坐标原点间的关系
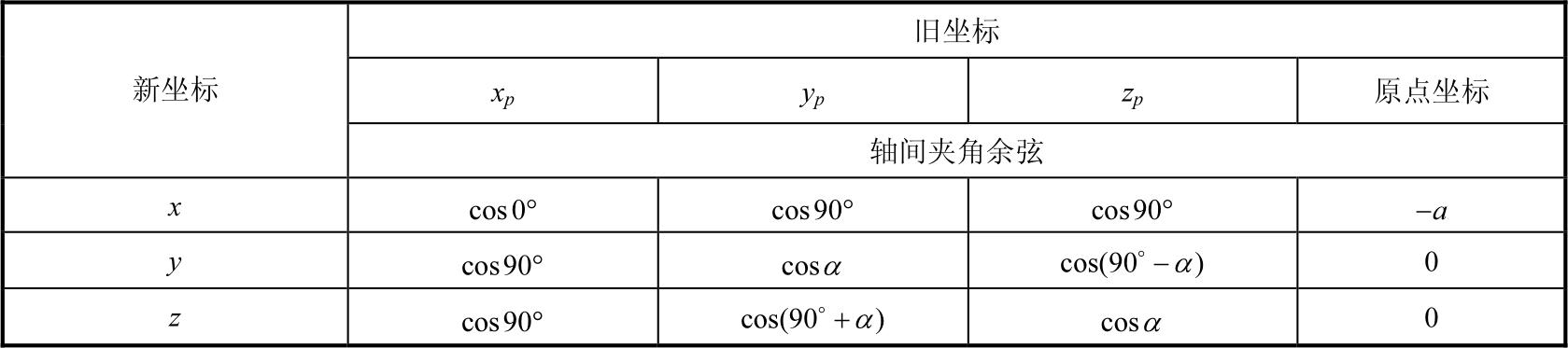
用关系式表示为

由坐标系 S p 变换到坐标系 S 的系数矩阵为
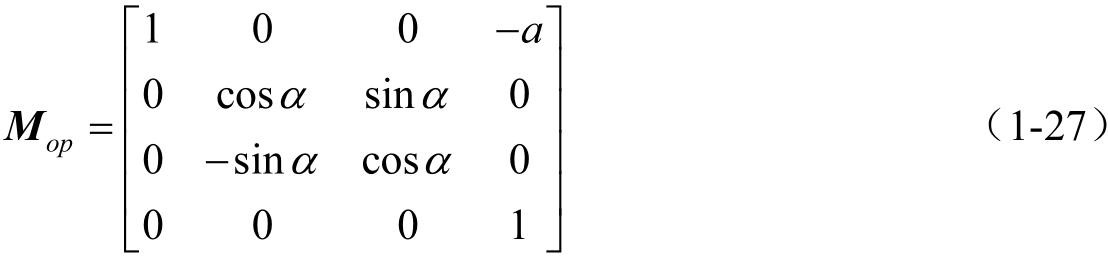
关于矩阵求逆计算可按下列公式进行。设将 M po 和 M op 写成普遍的形式
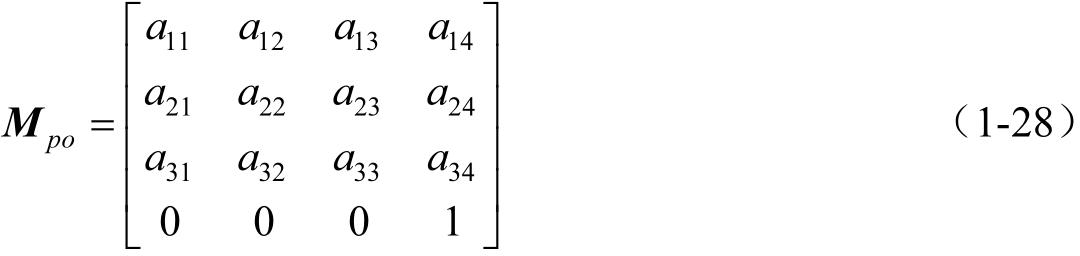
由于矩阵 M po 与 M op 中左上角3×3阶方阵既互为逆矩阵,又互为转置矩阵,于是
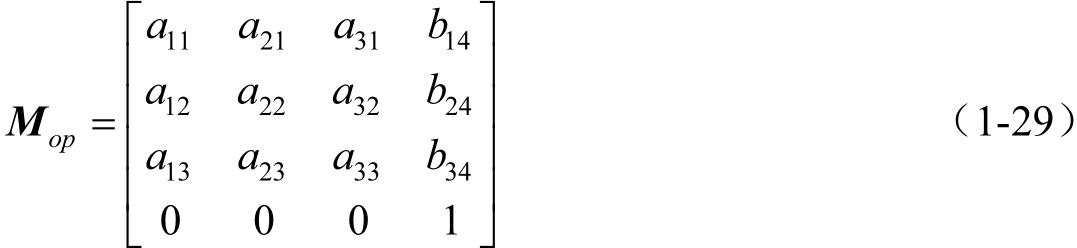
式(1-29)中, b 14 、 b 24 、 b 34 为 P 系坐标原点在0系中的三个坐标值,即

欲求坐标系 S 1 与坐标系 S 间的变换关系,可先列出坐标系 S 1 与 S 中各坐标轴间的方向余弦及坐标系原点间的关系,如表1-3所示。
表1-3 坐标系 S 1 与 S 中各坐标轴间的方向余弦及坐标系原点间的关系
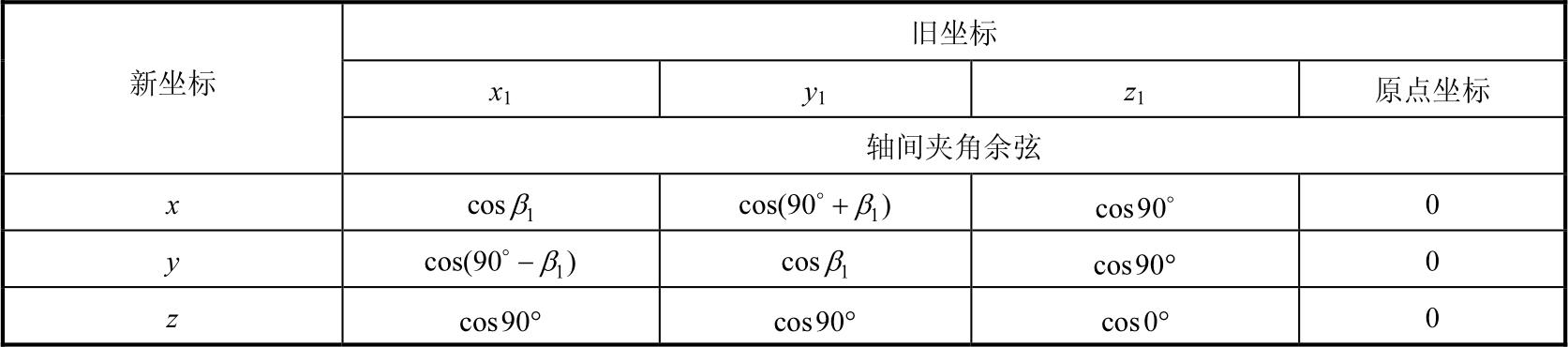
则有 S 1 变换到 S 的系数矩阵为
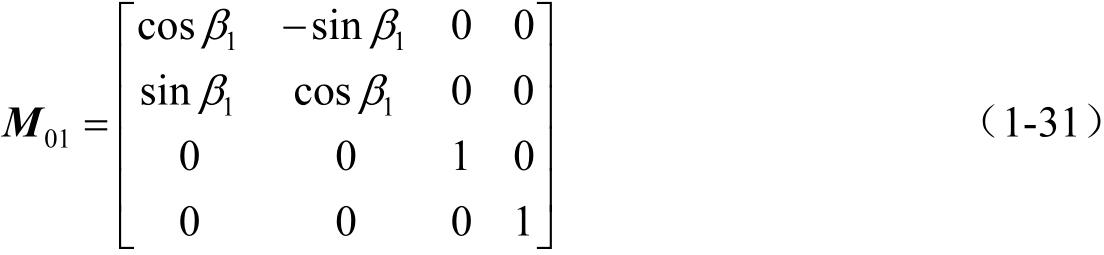
其坐标变换关系式为
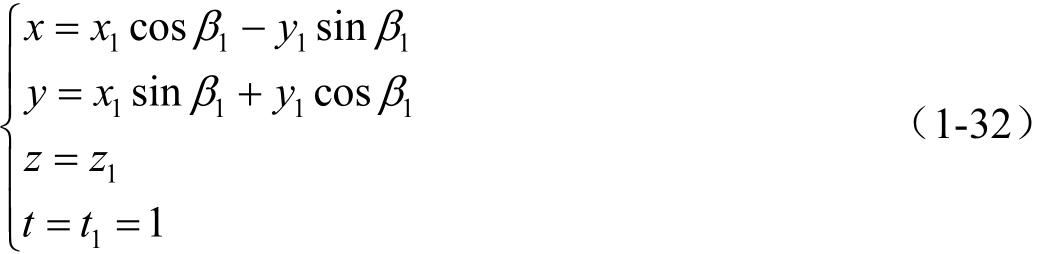
若由 S 变换到 S 1 ,其系数矩阵为 M 10 。而 M 10 与 M 01 中左上角3×3阶方阵既互逆又互为转置矩阵,于是
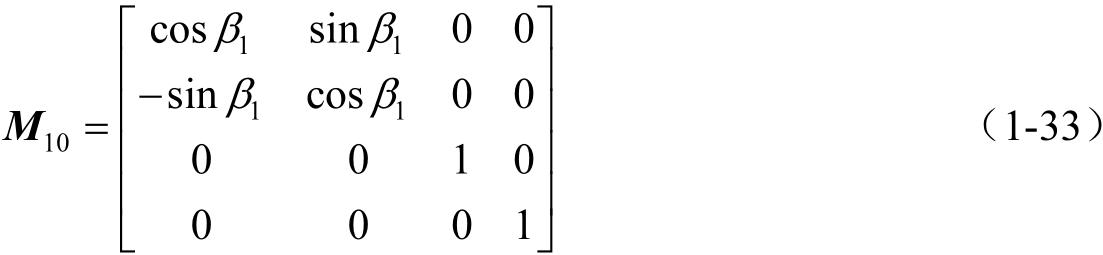
其坐标变换关系式为
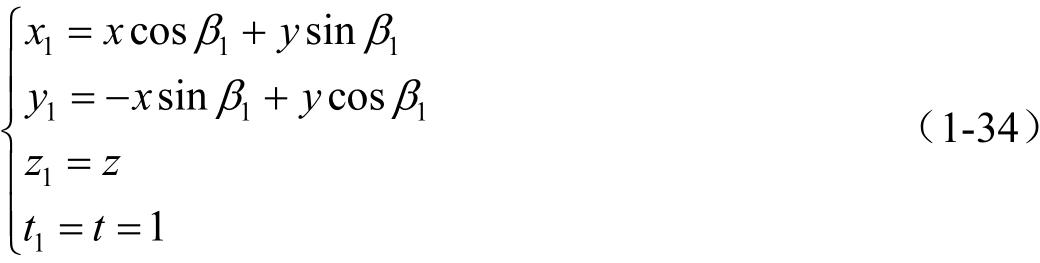
坐标系 S 2 与 S p 中各坐标轴间的方向余弦及坐标系原点间的关系如表1-4所示。
表1-4 坐标系 S 2 与 S p 中各坐标轴间的方向余弦及坐标系原点间的关系
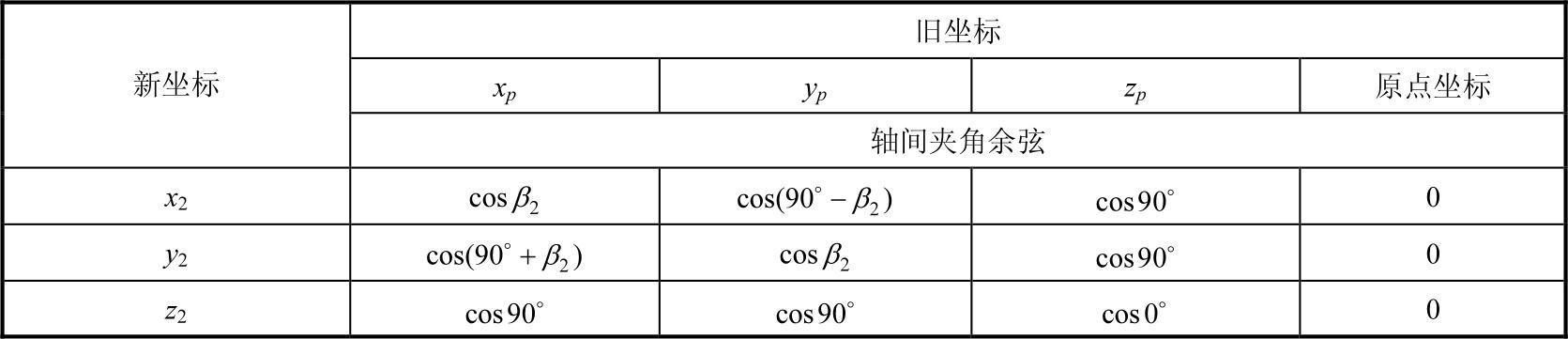
则由坐标系 S p 变换到 S 2 的系数矩阵为
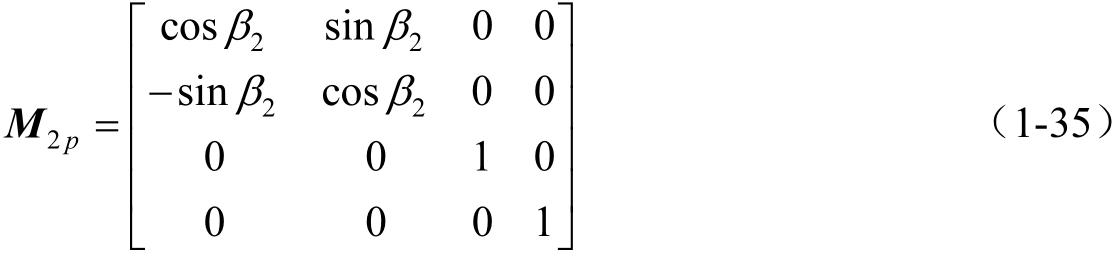
而将坐标系 S 1 变换到坐标系 S 2 ,坐标系变换公式为

式中, 1 r 、 r 2 为空间任意一点在坐标系 S 1 、 S 2 中的径矢; M 21 为由坐标系 S 1 变换到坐标系 S 2 的系数矩阵。
根据矩阵乘法定则可得:
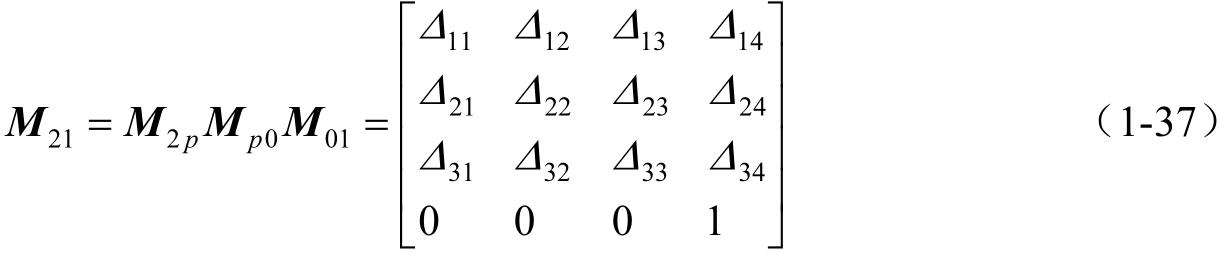
式中,
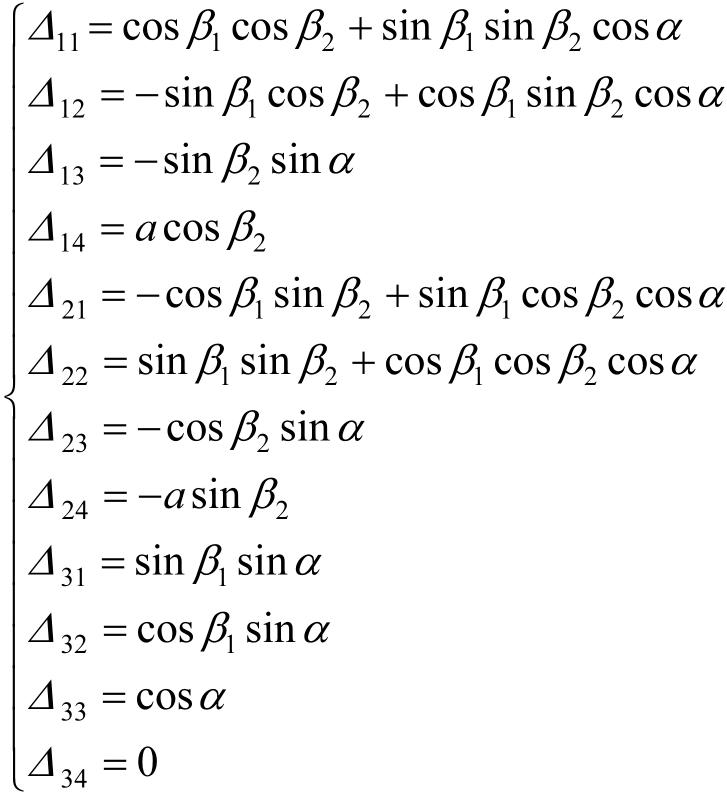
其坐标变换关系式为
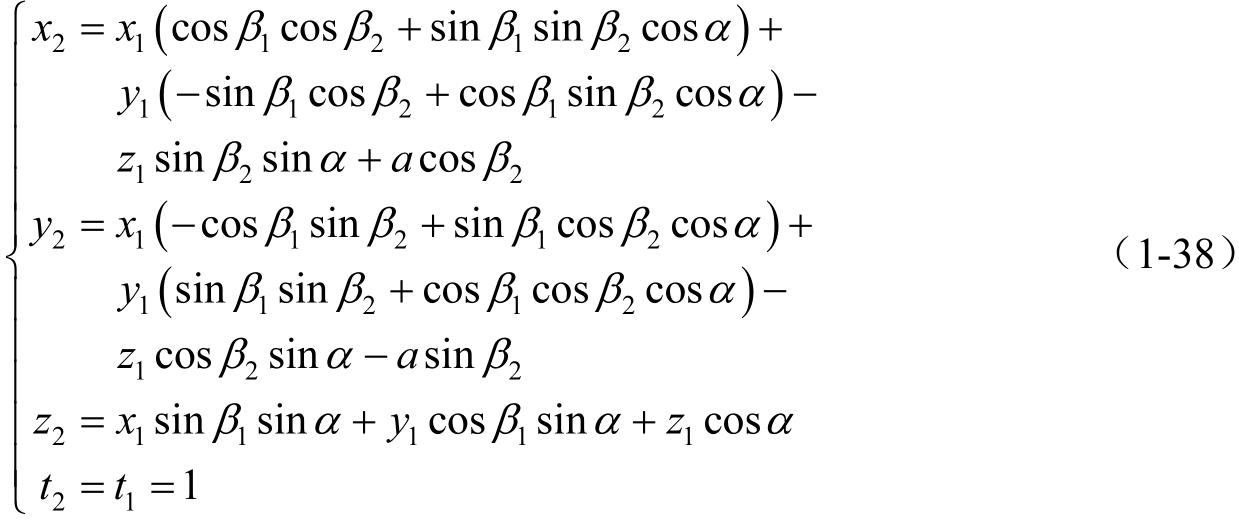
同理,由坐标系 S 2 变换至坐标系 S 1 时,坐标变换公式为

系数矩阵 M 12 与 M 21 中左上角3×3阶方阵既互逆,又互为转置矩阵,于是
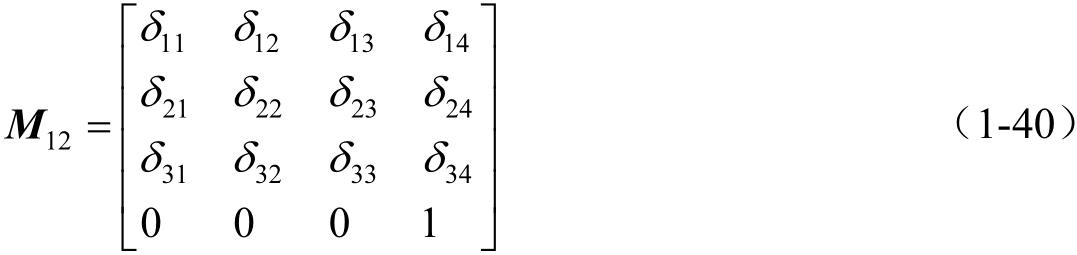
式中,
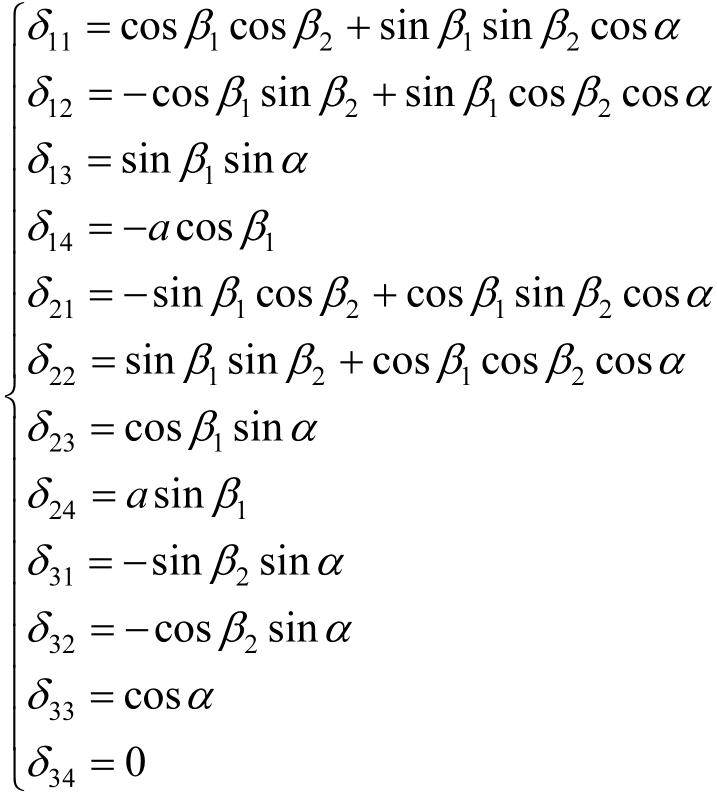
其坐标变换公式为
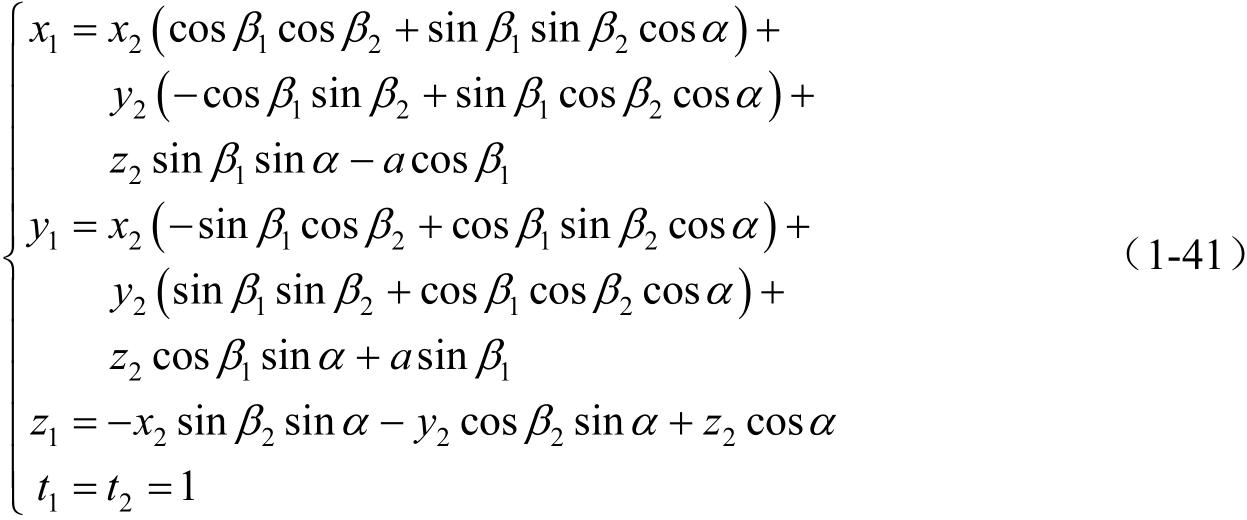
假定有两个坐标系 S m ( x m , y m , z m )和 S n ( x n , y n , z n ),推推假假推推如如1-8所所。
在坐标系 S m 中,点 M 用位置矢量表示

在坐标系 S n 中同一点 M 可用位置矢量和矩阵方程来确定。

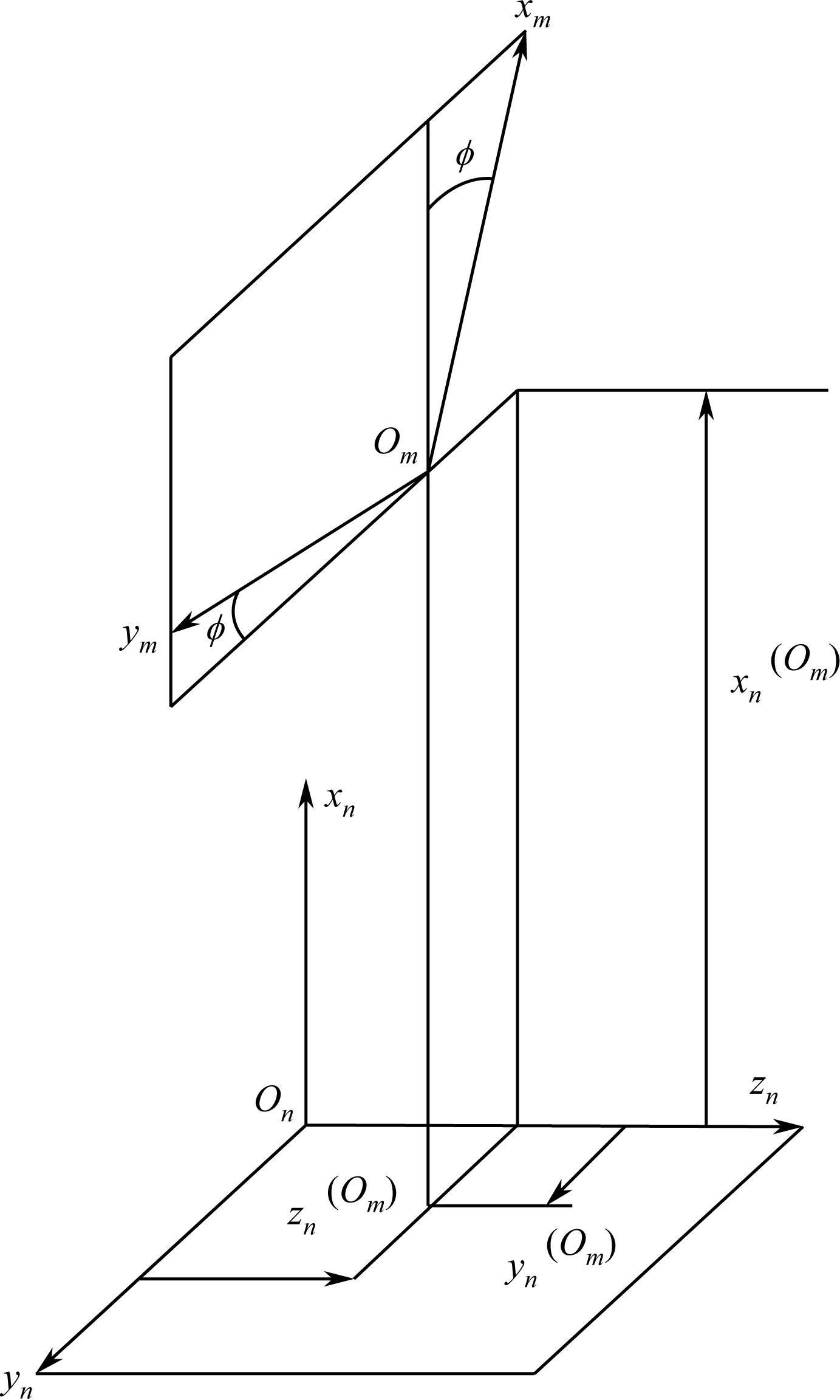
图1-8 推导坐标变换
矩阵 M nm 可以表示为
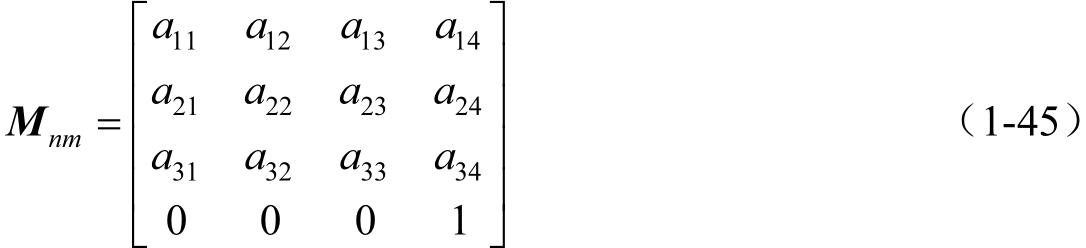
式中, M nm 中的下角标“ nm ”表明坐标变换是从 S m 到 S n 。矩阵 M nm 中元素 a kl ( k =1,2,3; l =1,2,3)的确定应基于以下规则。
(1)3×3子矩阵。

式中, a kl 的两个下角标表示“旧”坐标轴的号数 l 和“新”坐标轴的号数 k 。坐标轴 x 、 y 和 z 分别用号数1、2和3来表示。
(2)元素
a
14
、
a
24
和
a
34
表示“旧”原点
O
m
的“新”坐标
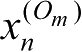 、
、
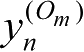 和
和
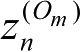 。
。
每一行(或列)的各个元素是单位矢量的方向余弦,于是

由于坐标轴单位矢量的正交性,则有
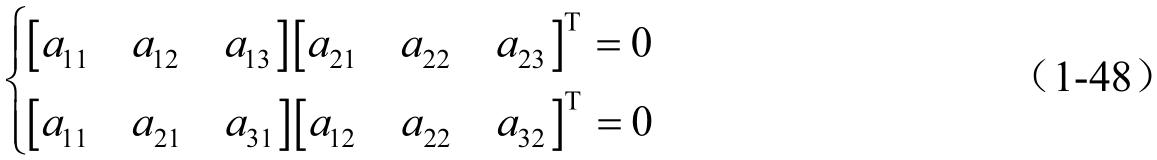
矩阵 L nm 的一个元素可以用相应的二次判别式来表示,如

利用4×4方矩阵和4×1列矩阵的乘法规则(列矩阵的行数等于矩阵 M nm 中的列数)可以确定点 M 的新坐标( x n , y n , z n )。由方程(1-44)可导出
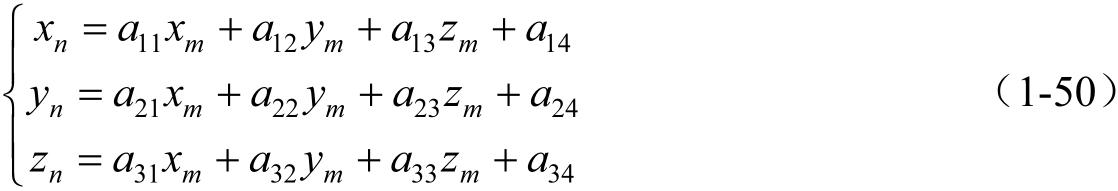
逆坐标变换的目的是要在给定坐标( x n , y n , z n )的情况下确定坐标( x m , y m , z m )。逆坐标变换用下列公式表示

如果矩阵 M nm 的判别式不为零,则存在逆矩阵 M mn 。
通过一个简单原则,可以利用正矩阵的元素来确定逆矩阵的各个元素。假定矩阵 M nm 用下式给定:
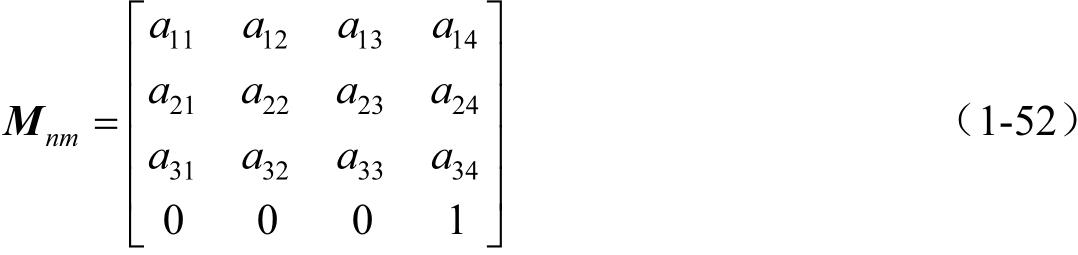
则须确定用
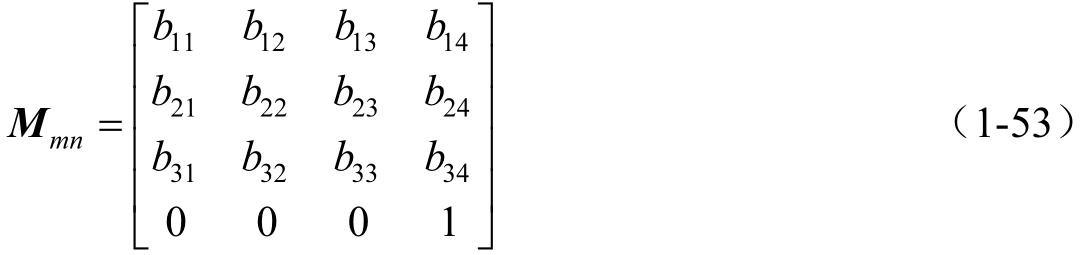
所表示的矩阵
M
mn
的各个元素。
M
mn
=
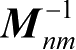 ,
M
mn
M
nm
=
E
,
E
是单位矩阵。
,
M
mn
M
nm
=
E
,
E
是单位矩阵。
其中,3×3子矩阵 L mn 的确定如下:

其余的元素( b 14 , b 24 和 b 34 )可利用下列方程来确定:
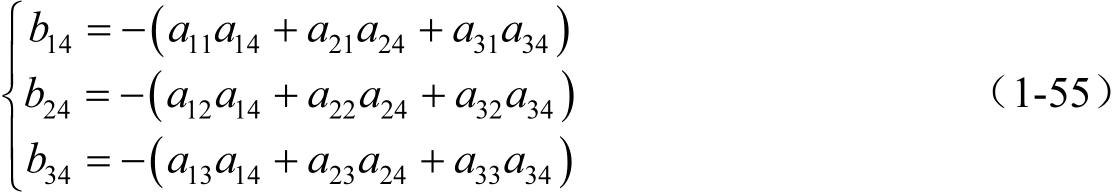
根据矩阵代数相乘规则,就可完成矩阵的逐次坐标变换。例如矩阵方程
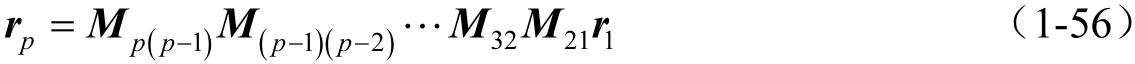
表示从 S 1 到 S 2 ,从 S 2 到 S 3 ,…,从 S ( p −1) 到 S p 的逐次坐标变换。
为了完成自由矢量分量的变换,仅需要采用3×3子矩阵 L (该矩阵由去掉相应矩阵 M 的最后一行和最后一列而得出)。这个结论从自由矢量的分量(在坐标轴上的投影)与坐标系原点的位置无关这一事实可以得出。
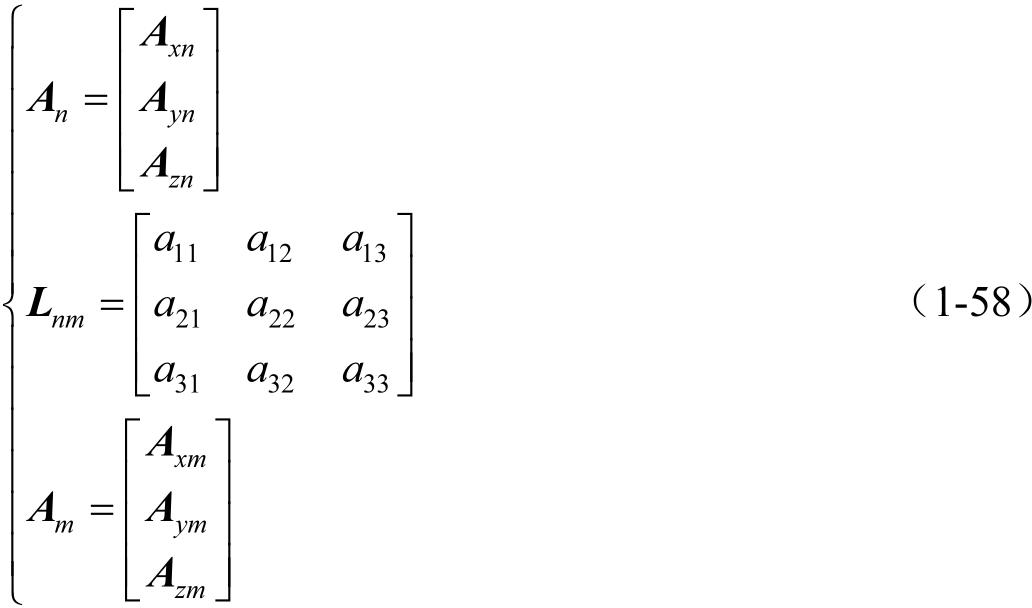
自由矢量 A 的分量从坐标系 S m 变换到 S n ,用下列矩阵方程表示:

式中,
法线矢量沿其作用线进行移动,因此齿轮齿面的法线矢量是滑动矢量。然而,如果被考察的曲面法线矢量所位于的曲面上的那一点同时进行转移,则曲面的法线矢量可变换为自由矢量。
基于应用转动和移动的4×4矩阵,本节利用一些实例来具体分析坐标变换与矩阵的关系。通过这些问题的解答可以获得齿轮啮合理论中坐标变换的实际经验。
例题1.1
坐标系
S
1
和
S
2
刚性固连到相对于固定坐标系
S
f
进行转动和移动的齿轮和齿条刀具上(图1-9)。坐标系
S
1
中的点
M
用位置矢量
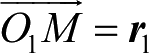 来表示。
来表示。
(1)确定同一点在坐标系 S 2 中的位置矢量 r 2 。
(2)通过矩阵
M
21
的各个元素表达逆矩阵
M
12
=
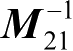 ,并且在
r
2
给定的情况下,确定位置矢量
r
1
。
,并且在
r
2
给定的情况下,确定位置矢量
r
1
。
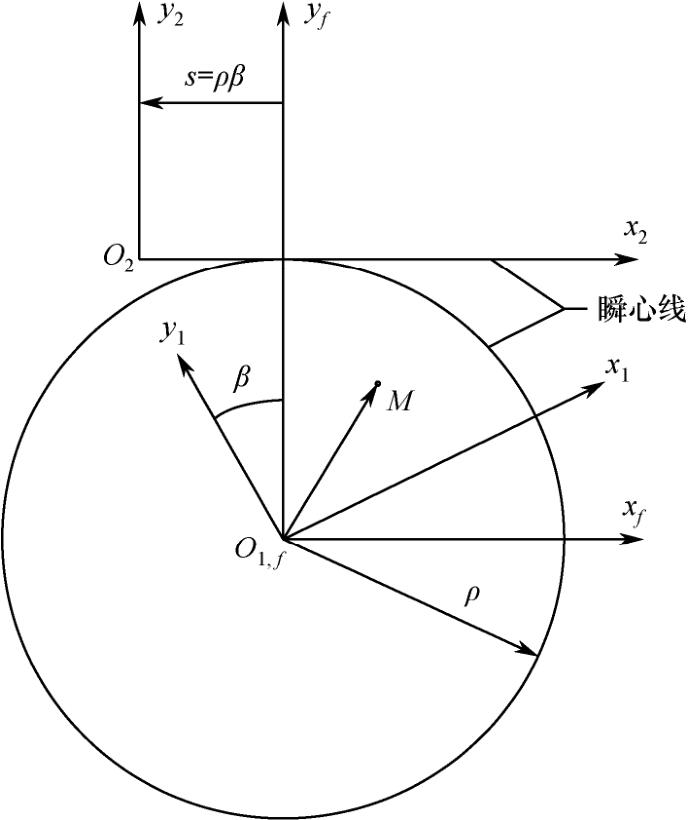
图1-9 直移—回转运动中的瞬心线
解: (1)从 S 1 到 S 2 的坐标变换基于矩阵方程

绕轴线 z f 的转动用矩阵 M f 1 来描述,则 z f 轴的单位矢量为

从 S 1 到 S 2 的转动是沿顺时针方向完成的,因此按照对应的运算符号来选取。由 c 1 = c 2 =0, c 3 =1,得到下列转动矩阵 M f 1 的表达式为
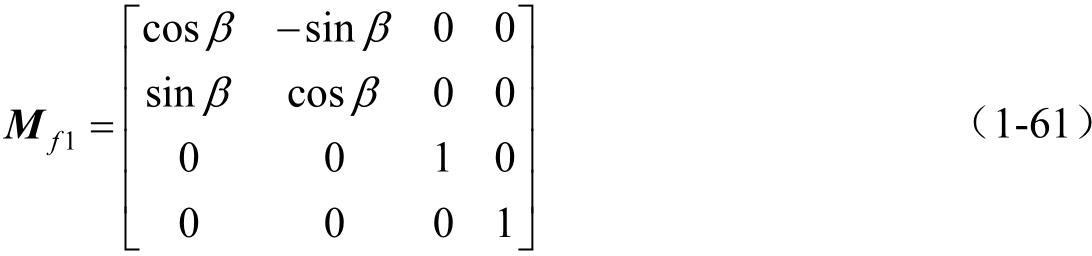
从图1-9的图形中,求导出

平移矩阵为
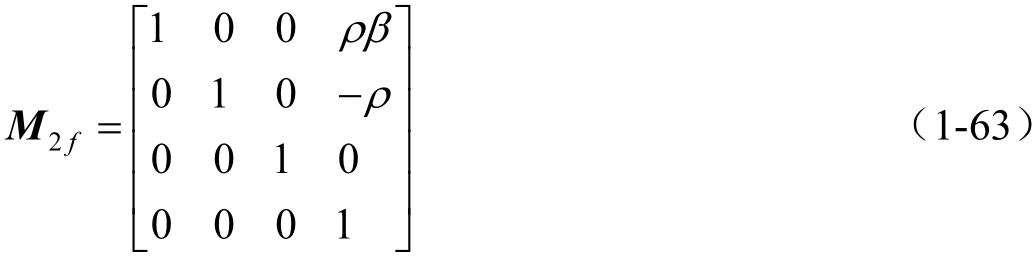
位置矢量 r 2 和 r 1 为

由方程(1-60)~(1-64)可导出
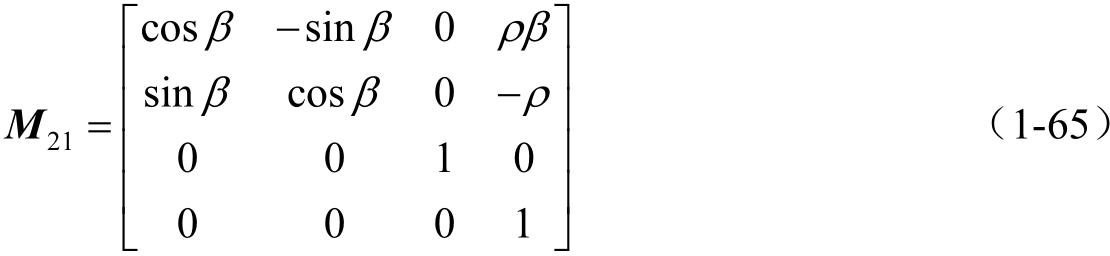
并且
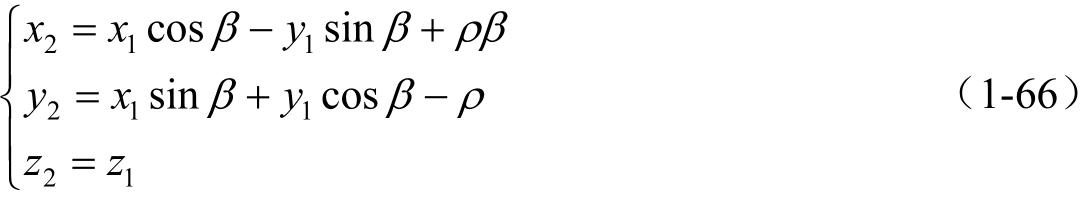
(2)矩阵
M
21
是非奇异的,从而存在逆矩阵。为了确定逆矩阵
M
12
=
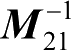 ,可利用方程(1-51)~(1-55)导出
,可利用方程(1-51)~(1-55)导出
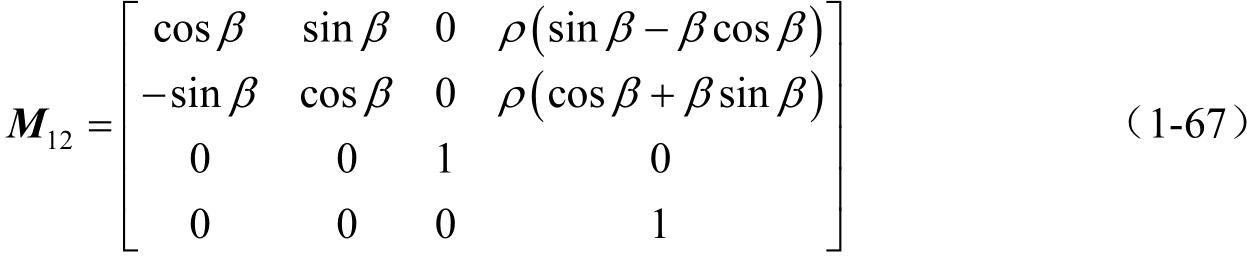
再利用矩阵方程

得到
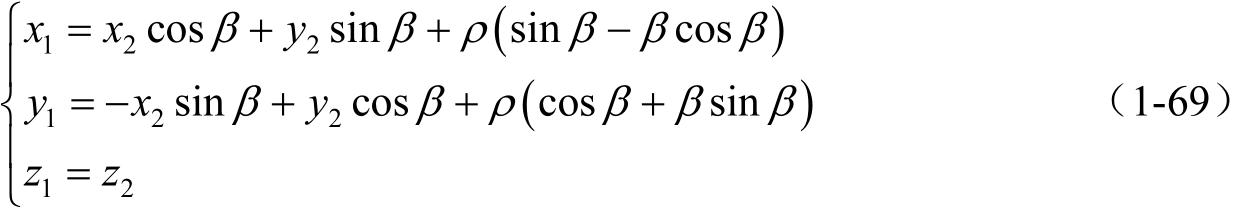
例题1.2 坐标系 S 1 ( x 1 , y 1 , z 1 )和 S 2 ( x 2 , y 2 , z 2 )刚性固接到齿轮1和齿轮2,两齿轮传递平行轴之间的回转运动,具有相反方向的回转运动瞬心线如图1-10所示。齿轮的两回转角 β 1 和 β 2 用方程(1-70)表示:

式中, ρ 1 和 ρ 2 是齿轮两瞬心线的半径。 E 是两转动轴线之间的最短距离。固定坐标系 S f 刚性连接到齿轮箱体上。 S p 是辅助坐标系,它也刚性连接到齿轮箱体上。
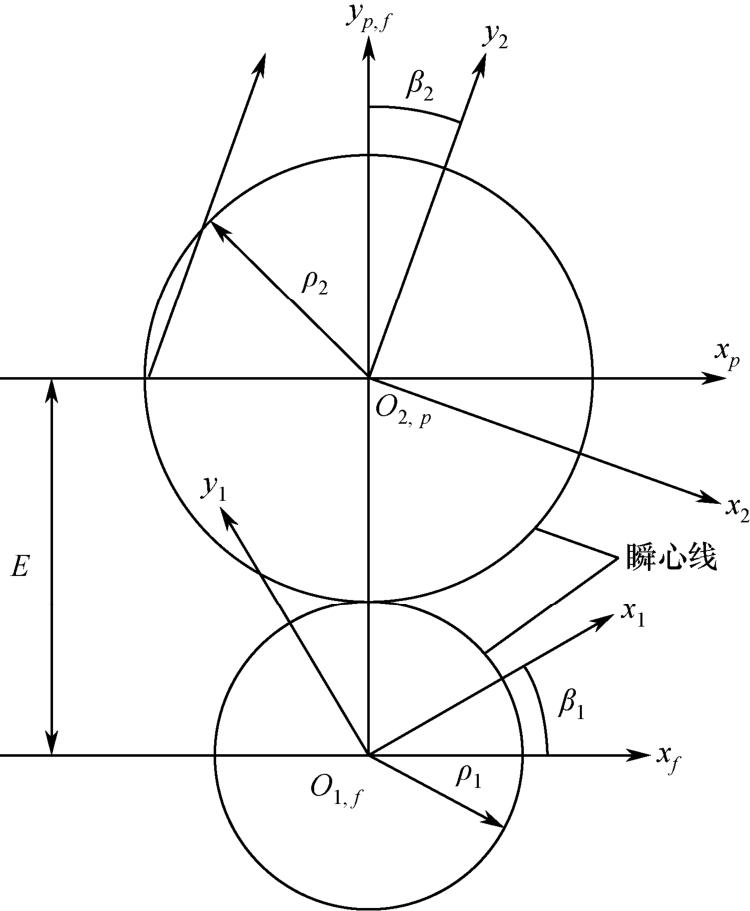
图1-10 具有相反方向的回转运动瞬心线
(1)求从 S 2 到 S 1 的坐标转换方程。
(2)求从 S 1 到 S 2 的坐标转换方程。
解: (1)从 S 2 到 S 1 的坐标变换基于矩阵方程

式中, M 1 f 和 M p 2 是转动矩阵, M fp 是移动矩阵。
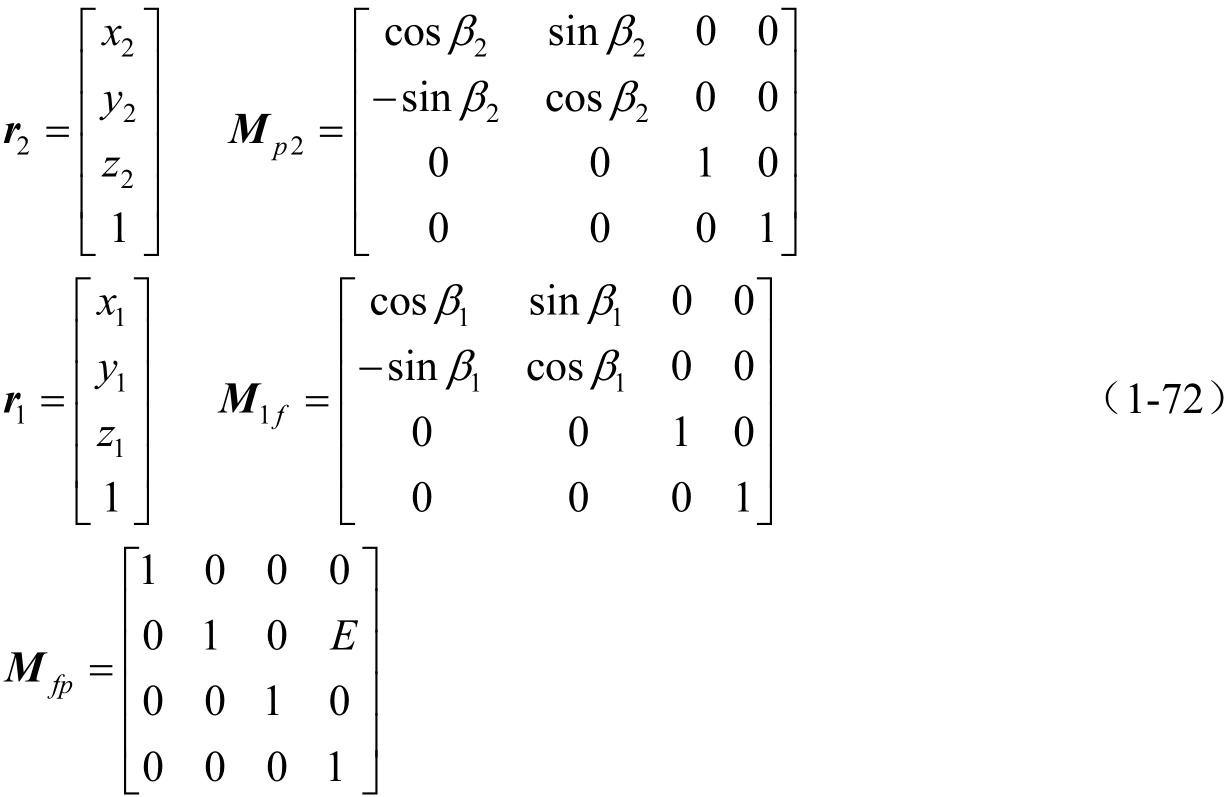
从方程(1-72)可导出
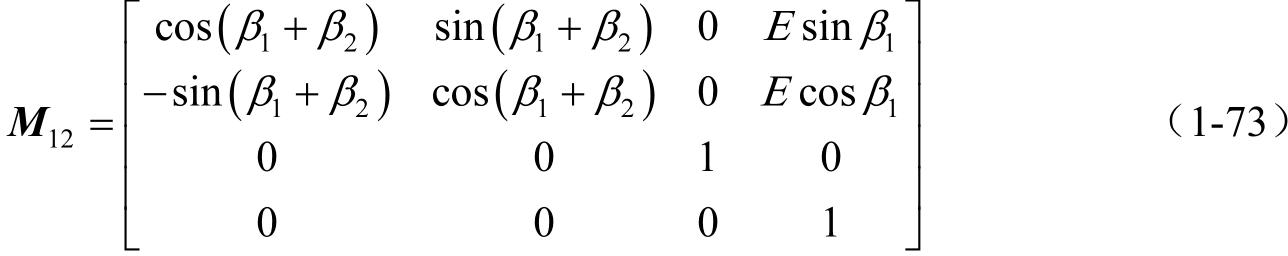
利用方程(1-71)和(1-73),我们可以得到
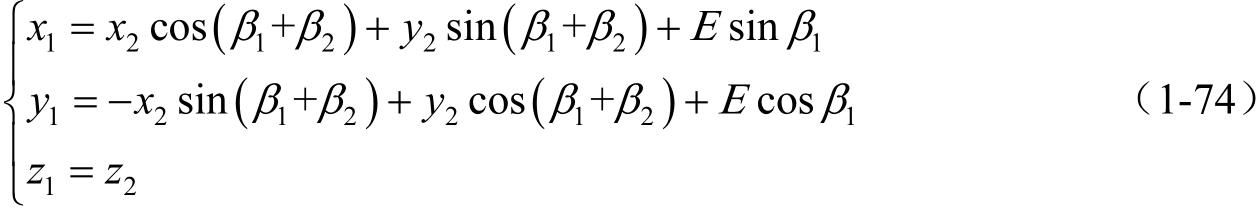
(2)逆矩阵
M
21
=
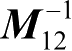 通过
M
12
的各元素参照方程(1-51)~(1-55)表达如下:
通过
M
12
的各元素参照方程(1-51)~(1-55)表达如下:
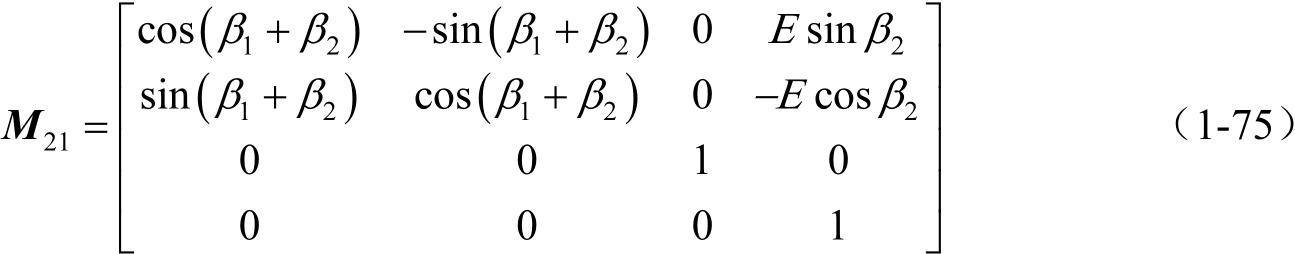
逆坐标变换基于矩阵方程

从该方程可导出
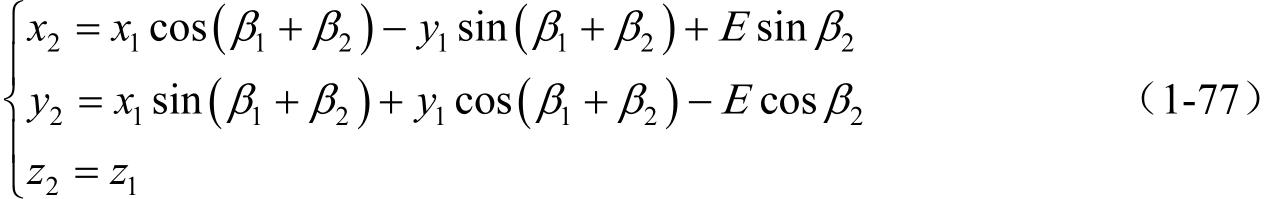
例题1.3 具有相同方向的回转运动瞬心线如图1-11所示,两齿轮绕两个平行轴线以相同的方向进行回转运动。坐标系 S 1 和 S 2 刚性固接于两齿轮1和2; S f 和 S p 是固定坐标系; E 是最短距离; ρ 1 和 ρ 2 是齿轮两瞬心线的半径。
(1)确定矩阵
M
21
=
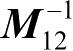 。
。
(2)完成从 S 1 到 S 2 以及 S 2 到 S 1 的坐标变换。
解:
(1) M 21 = M 2 p M pf M f 1
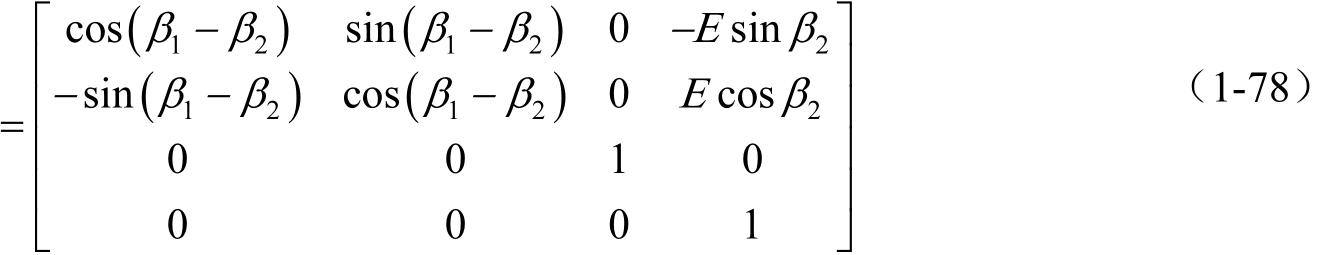
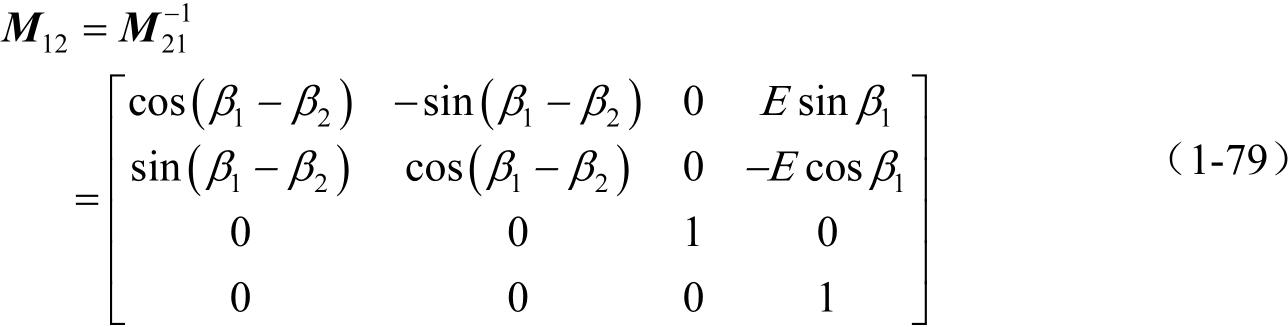
(2)
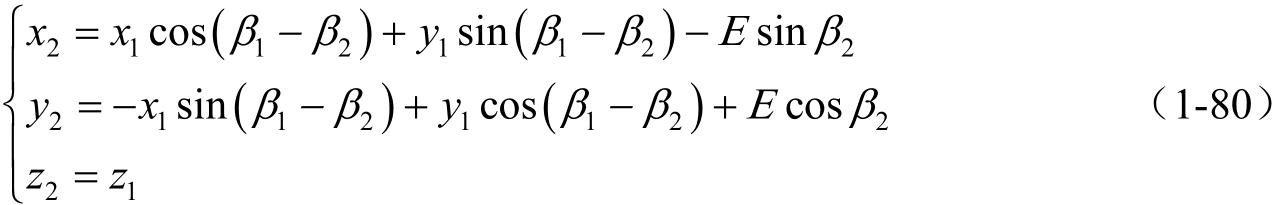
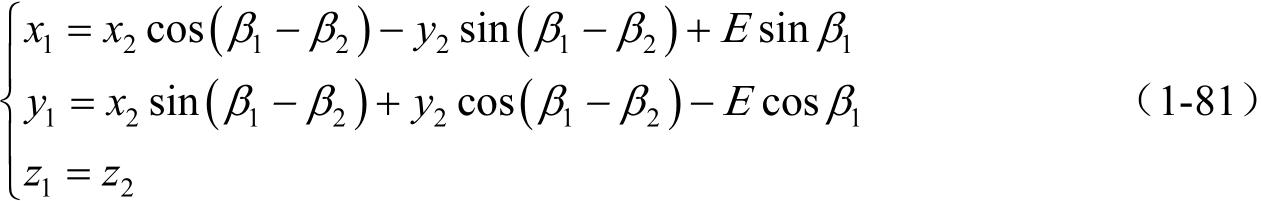
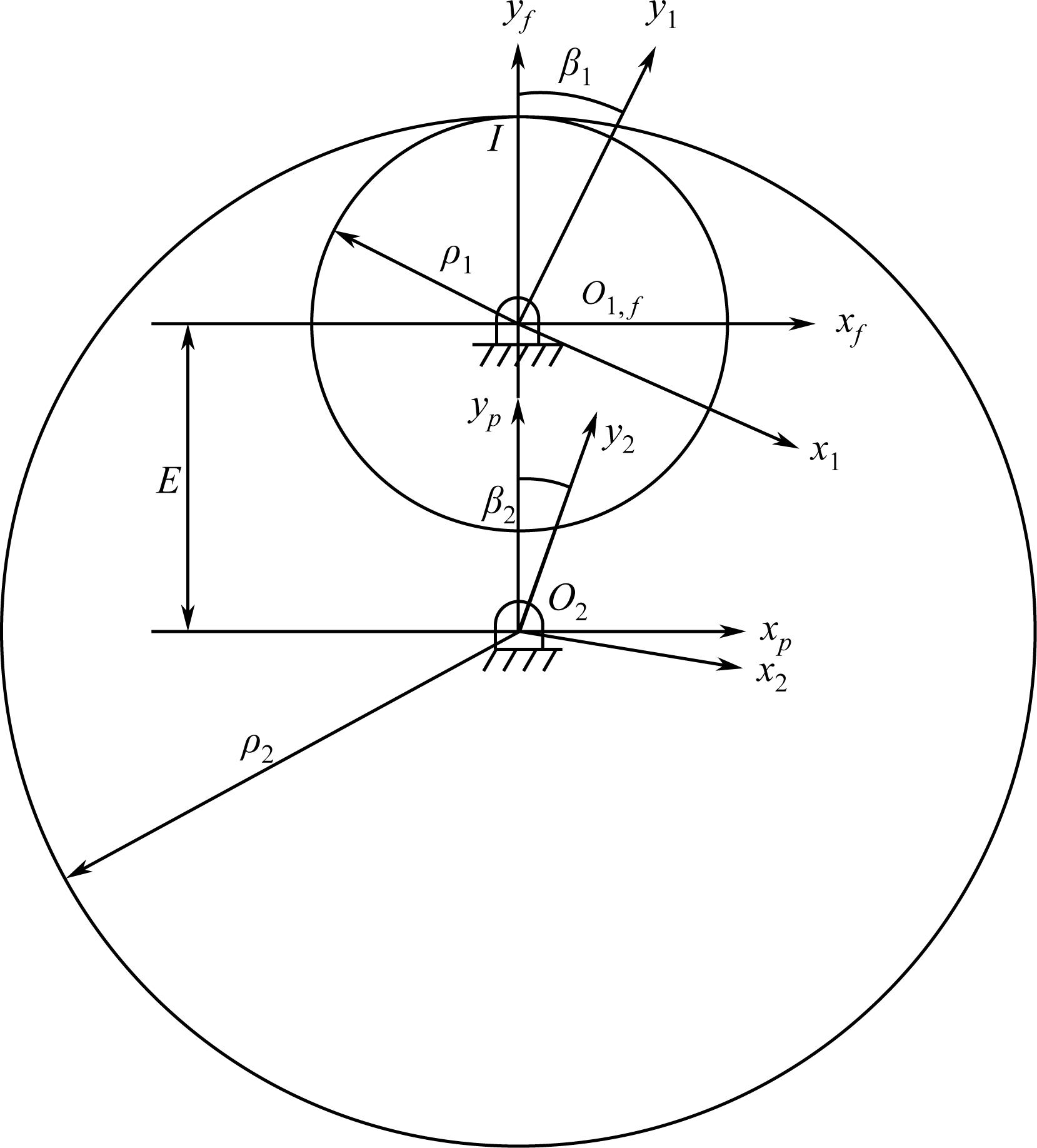
图1-11 具有相同方向的回转运动瞬心线