





假设由交错轴齿轮传动 (∑
(1)
,∑
(2)
) 建立图1-16所示的坐标,齿轮1、2固结的坐标系为S
1
、S
2
,S
0
(O
0
—x
0
,y
0
,z
0
)及S
d
、S
p
是三个在空间固定的坐标系。S
0
坐标系的z
0
轴与齿轮 2 的回转轴 z
2
重合;S
d
坐标系与 S
0
坐标系之间相差一个平移
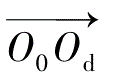 [0 G-E];S
p
坐标系与S
d
坐标系之间相差一个平移
[0 G-E];S
p
坐标系与S
d
坐标系之间相差一个平移
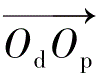 [0 0 P]和90°-γ的旋转。大小轮的回转角速度分别为ω
2
、ω
1
,任意瞬时的转角分别为φ
2
、φ
1
。
[0 0 P]和90°-γ的旋转。大小轮的回转角速度分别为ω
2
、ω
1
,任意瞬时的转角分别为φ
2
、φ
1
。
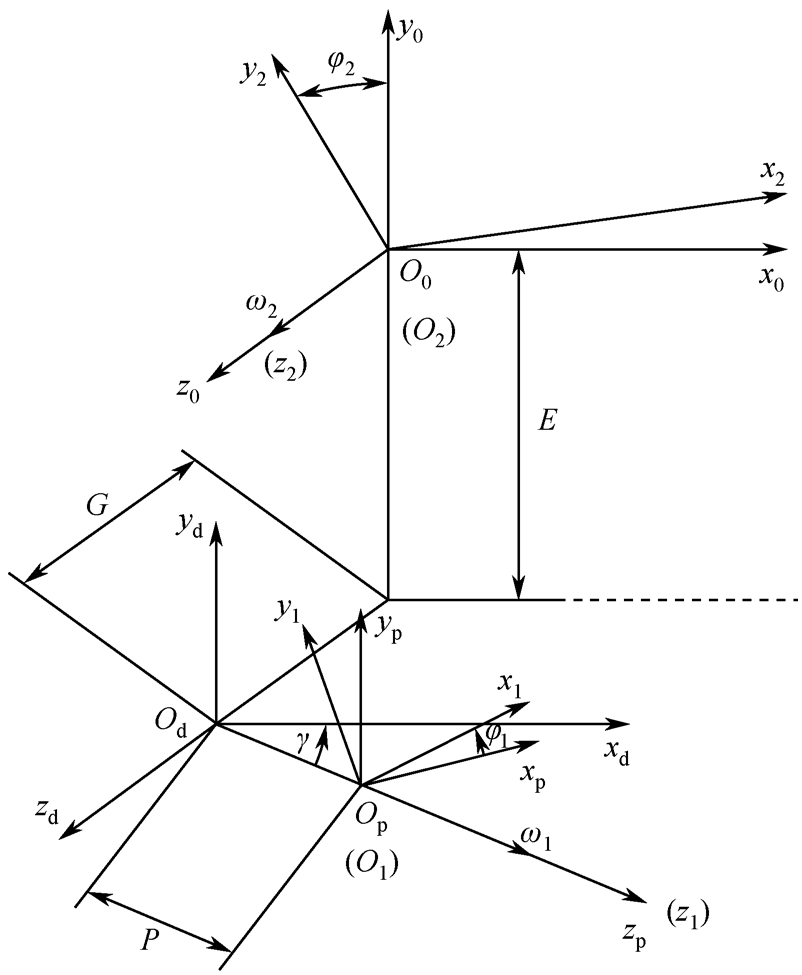
图1-16 坐标系的变换
根据坐标转换关系可知,坐标系S 2 到S 0 的旋转变换矩阵为
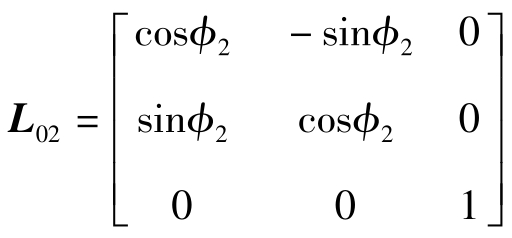
坐标系S 1 到S p 的旋转变换矩阵为
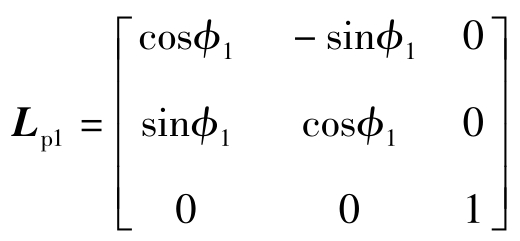
坐标系S p 到S d 的齐次变换矩阵为
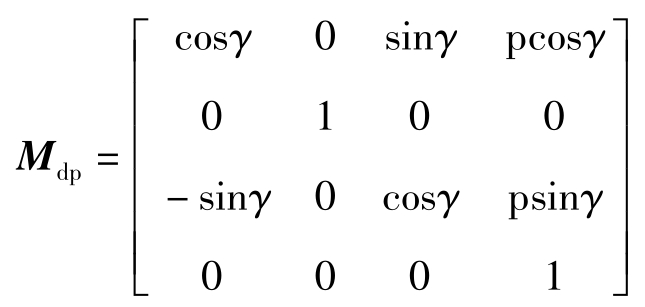
坐标系S d 到S 0 的齐次变换矩阵为
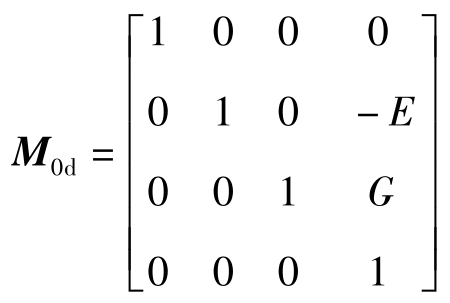
大小轮接触点的相对运动速度为
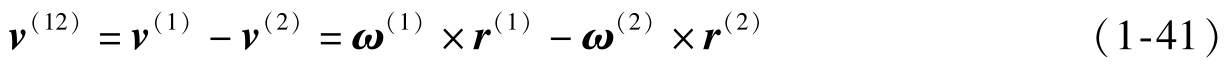
因为r
(2)
=r
(1)
-R
12
,
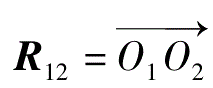 ,所以相对运动速度式 (1-41) 可表示为
,所以相对运动速度式 (1-41) 可表示为
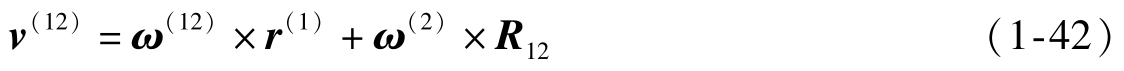
可进一步在坐标系S 0 中表示。先将有关各矢量代入S 0 坐标系中,大轮径矢量为
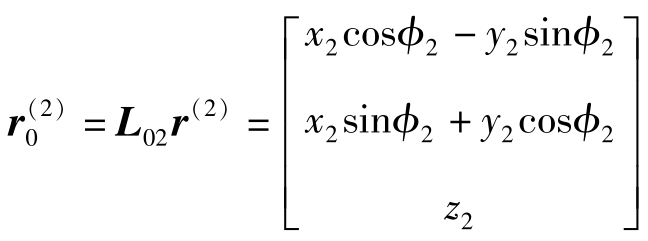
大轮坐标原点指向小轮轴线 (可以是小轮轴线上任意一点) 的矢量为
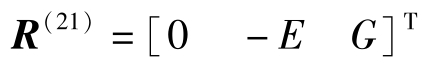
大小轮的角速度为
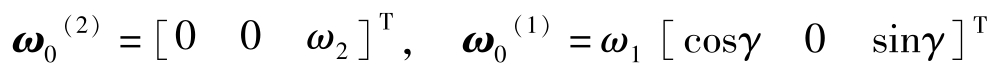
把上述各量代入式 (1-42),化简后可得
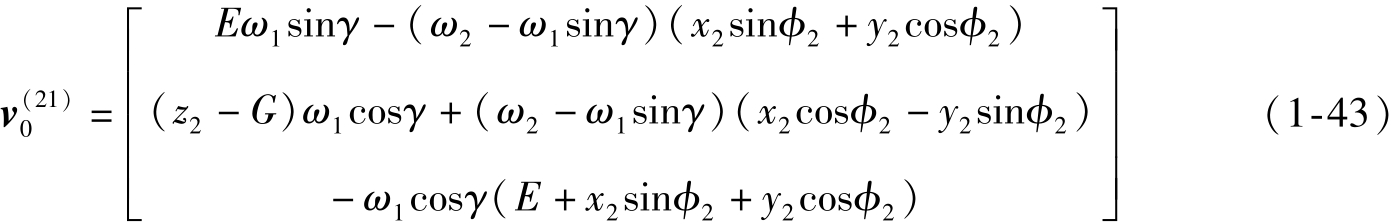
如果已知的量是r 1 坐标,则v (12) 在S p 坐标系中的表示会简单一些,这时各矢量表示如下:
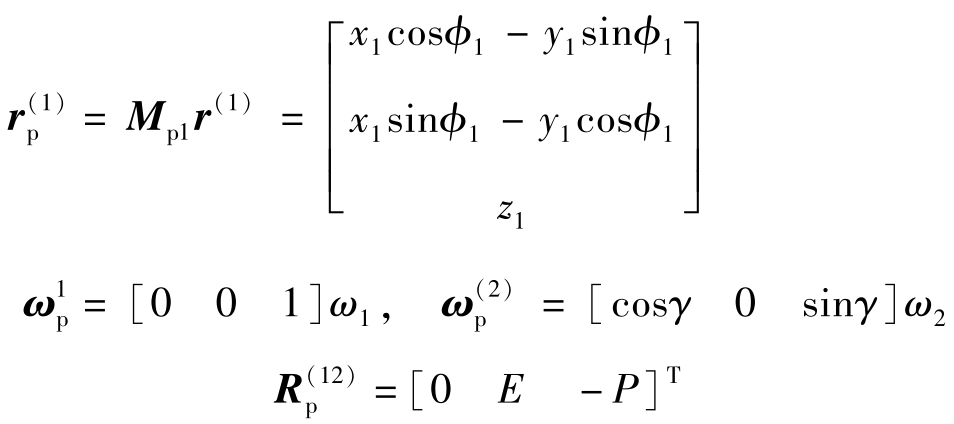
则
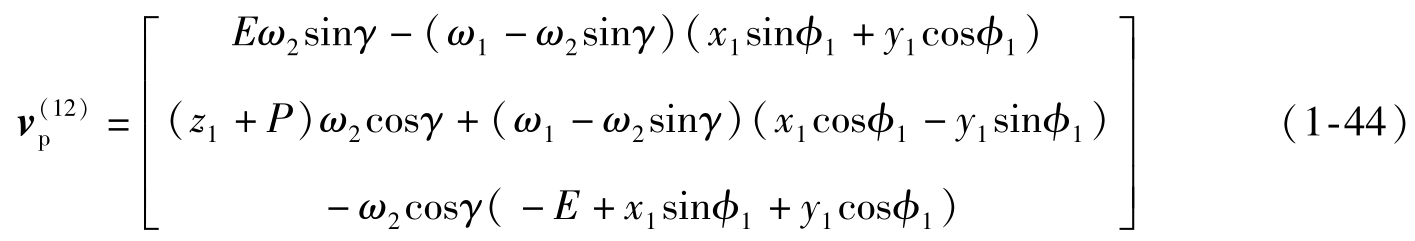
如果把v (21) 表示到S 2 坐标系中,则v 2 (21) 不能直接利用v 0 (21) 做坐标变换,而必须把运算前的矢量先变换到S 2 坐标系中,这时
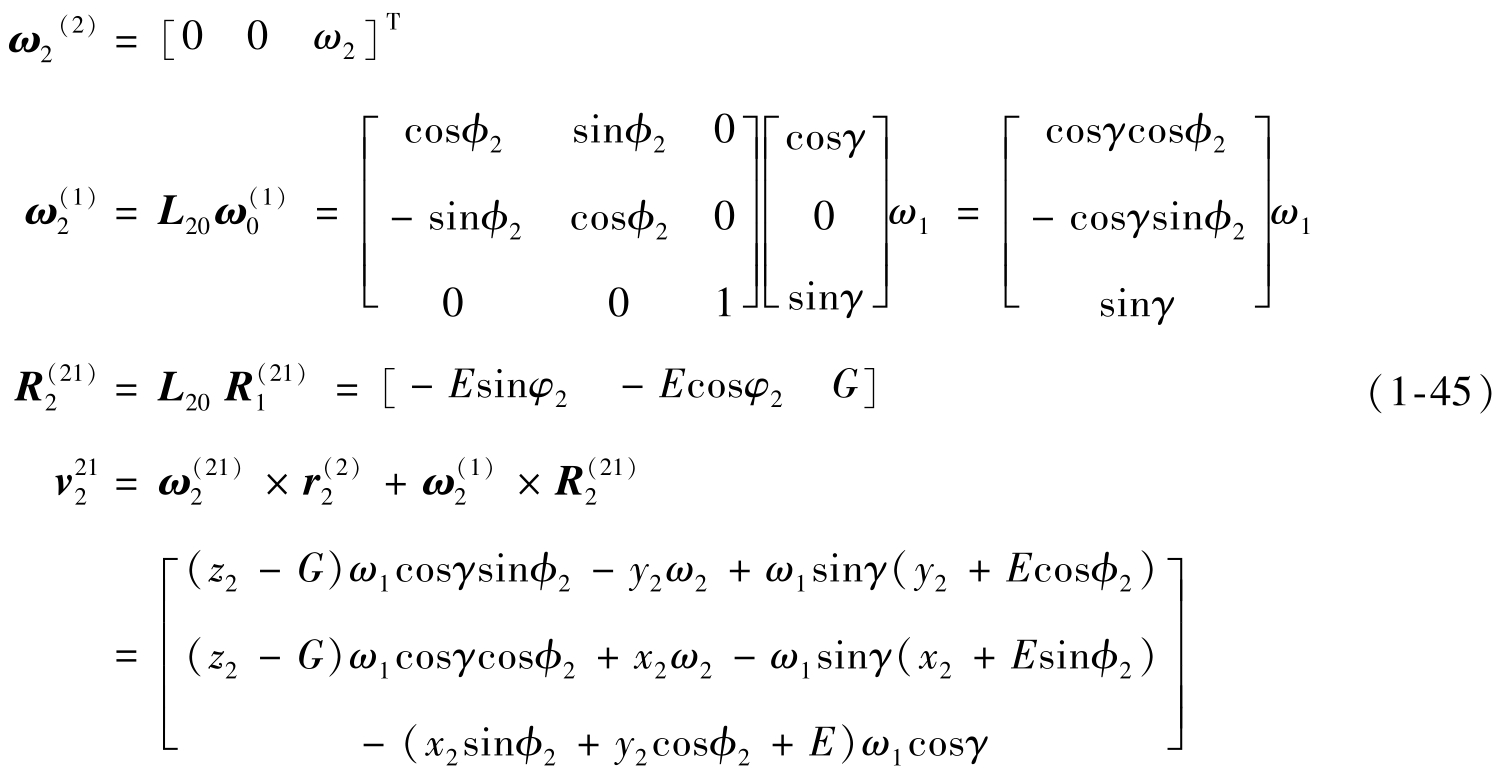
假设产形轮∑ (2) 曲面参数为u、θ,齿面方程用r 2 (u,θ)=[x 2 ,y 2 ,z 2 ] T 表示,根据图1-16坐标系中的相应关系,可由啮合方程

推出
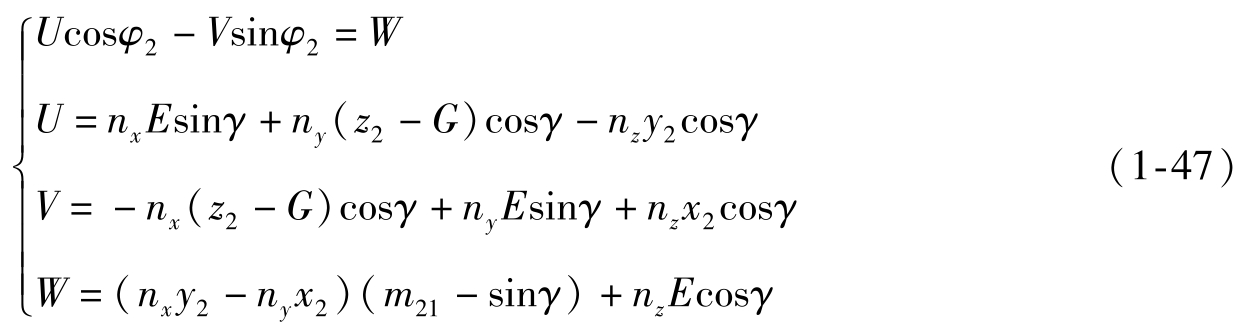
式 (1-47) 中的坐标、法矢量是在S
2
坐标系中的表达,在其他坐标系中可以有类似的表达形式。
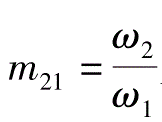 为啮合传动比。
为啮合传动比。
(1) 当γ=0时,为正交交错轴传动,例如蜗轮蜗杆、准双曲面齿轮传动等。这时啮合方程为
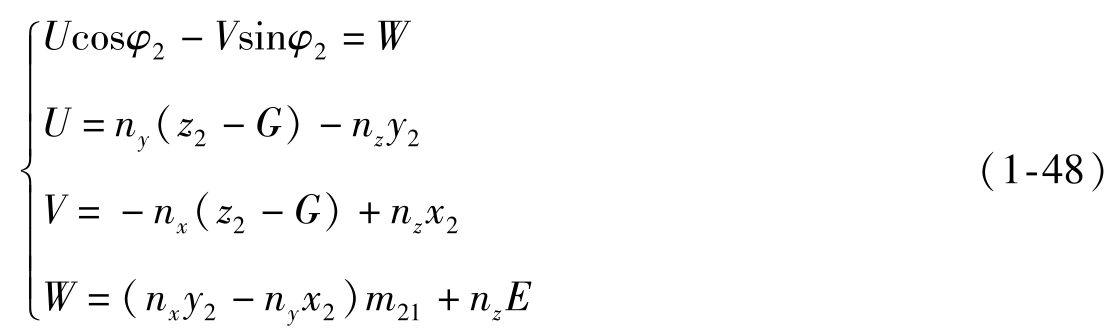
(2) 当γ=90°或-90°时,为平行轴内、外齿轮传动。这时啮合方程为
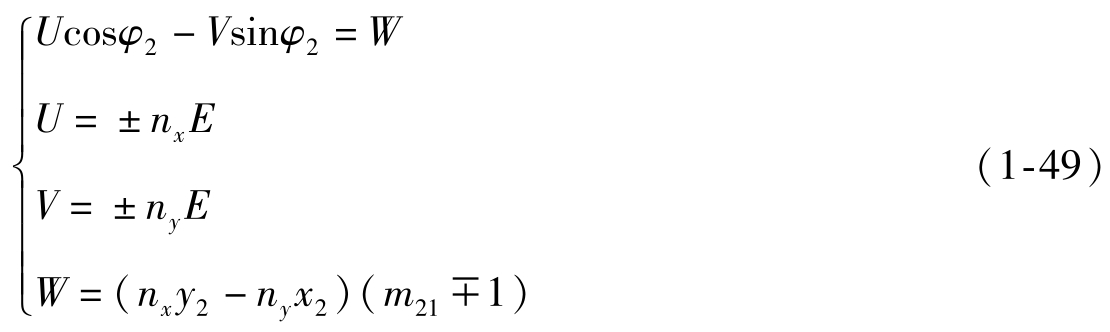
式中,“+” 对应内啮合,“-” 对应外啮合。
(3) 当E=0时,为相交轴传动,例如锥齿轮啮合传动。这时啮合方程为
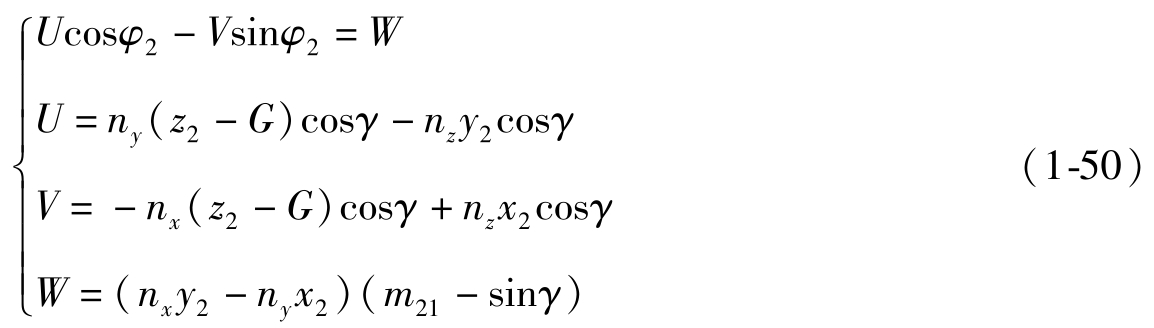
利用啮合方程式 (1-47) 或式 (1-48)~式(1-50) 可以解出
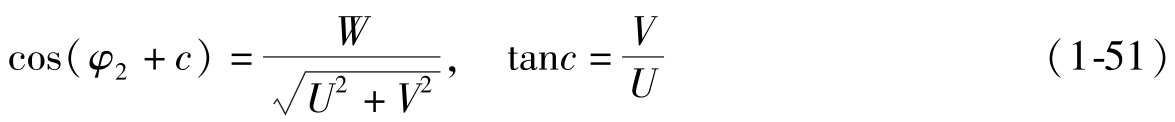
啮合方程一般都可化作式 (1-48)~式(1-51) 的形式。由式 (1-51) 可以解出φ
2
=φ
2
(u,θ)的关系,其几何意义是指转过φ
2
角,参数为 (u,θ) 的点成为啮合点。对于一定的转角φ
2
,一般有一系列的 (u,θ) 点对应,这些点构成了齿面2上的瞬时接触线。与此对应,齿面1上具有相应的啮合点与瞬时接触线,这些啮合点与瞬时接触线构成了齿轮1的齿面r
1
(u,θ)。角度φ
2
、φ
1
之间的关系为
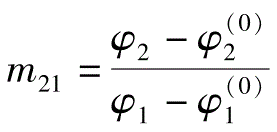 ,因初始转角通常取为零,所以
,因初始转角通常取为零,所以
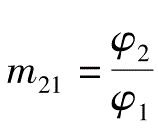 。
。
因为已知齿轮2的齿面方程,通过S 2 坐标系到S 1 齐次坐标变化,就可以求得与其共轭的小轮齿面方程:
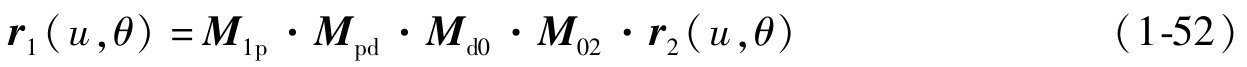
式 (1-52) 同1.2节的方法异曲同工,都可以解决共轭曲面的包络问题。