




一型T-S模糊系统是表示光滑非线性系统的有力工具。一般地,两种方法可以获得一型T-S模糊模型 [18,19] 。第一种方法主要基于系统的输入-输出数据,并运用系统辨识算法获得一型T-S模糊模型。当无法获得非线性系统的数学模型,而系统的输入-输出数据又可以获得时,主要采用这一方法。第二种建模方法主要适合于非线性系统数学模型已知的情形。当非线性系统的数学模型已经被建立时,运用扇区非线性法或局部近似方法可以获得期望的一型T-S模糊模型。一般地,一型T-S模糊模型可以通过如下的规则描述。
系统规则
i
:如果
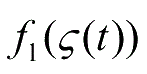 是
是
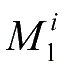 ,且……,且
,且……,且
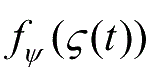 是
是
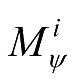 ,则
,则

式中,
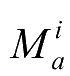 为相关于函数
为相关于函数
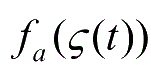 的一型模糊集,
a
=1,2,…,
Ψ
,
i
=1,2,…,
p
;
的一型模糊集,
a
=1,2,…,
Ψ
,
i
=1,2,…,
p
;
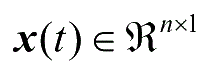 为状态向量;
为状态向量;
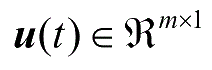 为控制输入向量;
为控制输入向量;
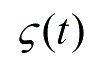 为前提变量。
为前提变量。
经过单点模糊,乘积推理,加权平均去模糊化可得全局模型为
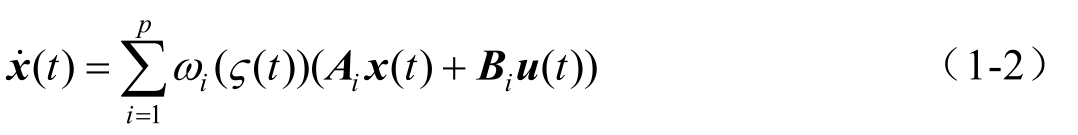
其中
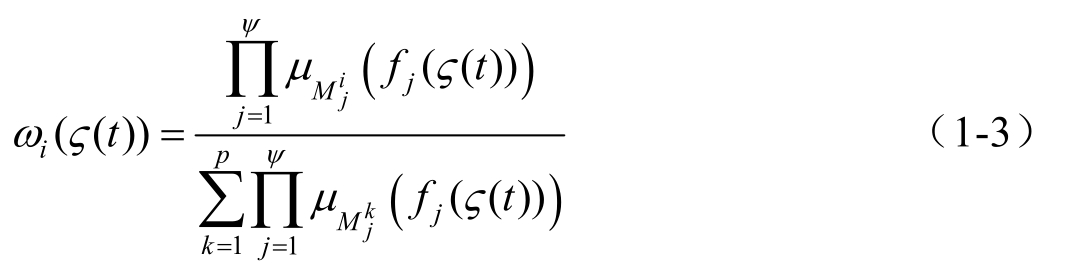

式中,
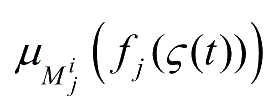 为隶属度,
为隶属度,
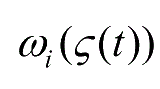 为模糊权重。
为模糊权重。
针对已经建立的一型T-S模糊模型,PDC策略常常用来设计各类模糊反馈控制器(如状态反馈控制器、静态输出反馈控制器、动态输出反馈控制器、基于观测器的状态反馈控制器)。PDC 策略的主要思想就是模糊控制器与模糊系统分享相同的前提隶属函数。基于PDC策略,一型T-S模糊状态反馈控制器可以定义如下。
控制器规则
i
:如果
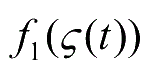 是
是
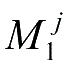 ,且……,且
,且……,且
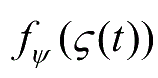 是
是
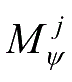 ,则
,则

式中,
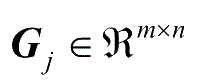 (
j
=1,2,…,
p
)为控制器的反馈增益。
(
j
=1,2,…,
p
)为控制器的反馈增益。
于是,全局的PDC状态反馈控制器可定义为

结合式(1-2)和式(1-6),在 PDC 策略下,一型 T-S 模糊闭环系统可以定义为
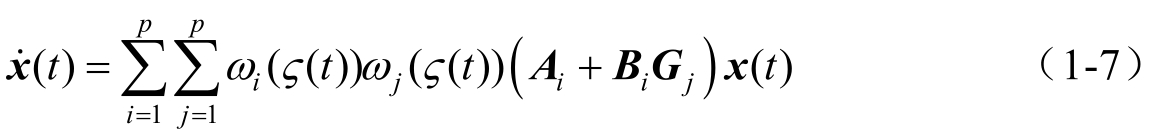
接下来,很多文献就是致力于找到反馈增益矩阵 G j ( j =1,2,…, p ),使得一型T-S模糊闭环系统式(1-7)渐近稳定 [53~59] 。
然而,当一型T-S模糊系统的模糊权重包含不确定信息时,PDC策略将失效。文献[30,31,60~62]提出了基于non-PDC策略的模糊状态反馈控制器。本书所指的 non-PDC 策略不要求模糊控制器与模糊系统分享相同的前提隶属函数,因此non-PDC策略比PDC策略具有更大的设计自由度。基于non-PDC 策略,一型T-S模糊状态反馈控制器可以定义如下。
控制器规则
j
:如果
g
1
(
θ
(
t
))是
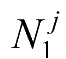 ,且……,且
g
Ψ
(
θ
(
t
))是
,且……,且
g
Ψ
(
θ
(
t
))是
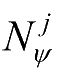 ,则
,则

于是,全局的non-PDC状态反馈控制器可定义为

其中
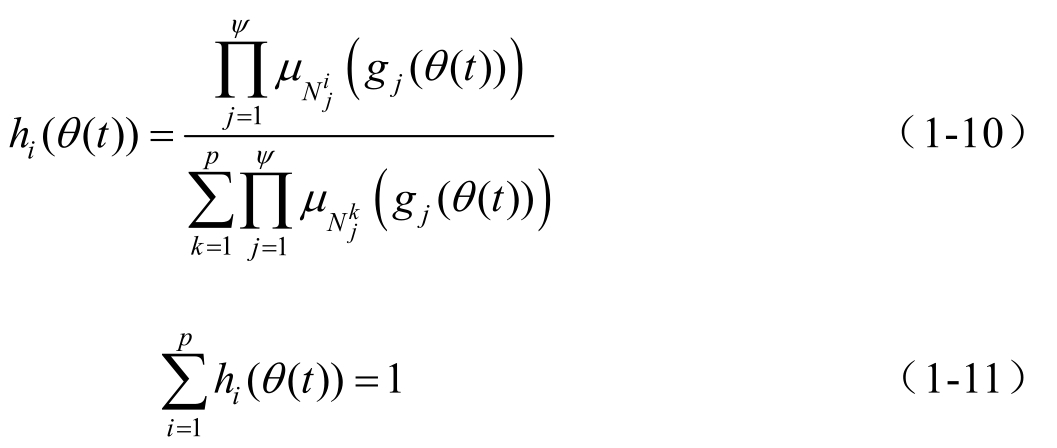
类似地,
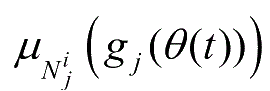 表示隶属度,
h
i
(
θ
(
t
))表示模糊权重。在non-PDC技术下,模糊控制器的模糊权重与模糊系统的模糊权重不相同,即
表示隶属度,
h
i
(
θ
(
t
))表示模糊权重。在non-PDC技术下,模糊控制器的模糊权重与模糊系统的模糊权重不相同,即
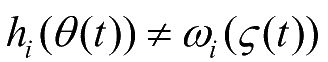 ,
i
=1,2,…,
p
。结合式(1-2)和式(1-9),在non-PDC策略下,一型T-S模糊闭环系统可以定义为
,
i
=1,2,…,
p
。结合式(1-2)和式(1-9),在non-PDC策略下,一型T-S模糊闭环系统可以定义为
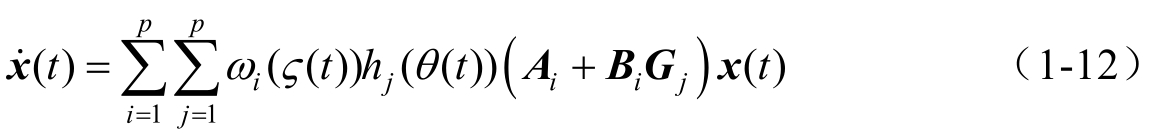
因为前提变量 θ ( t )可以自由选择,式(1-9)中的 non-PDC 控制器比式(1-6)中的PDC控制器具有更强的鲁棒性。然而,non-PDC策略不再具有PDC策略的某些优点,特别是很多减少保守性的方法不能用于non-PDC策略。于是,基于李雅普诺夫稳定性理论寻找式(1-12)中的 G j ( j =1,2,…, p ),通常具有较多的保守性。
无论是对于PDC策略还是non-PDC策略,如何减少设计条件的保守性,成为当前研究的重要课题。到现在为止,主要有三种方法减少设计条件的保守性。
(1)利用模糊隶属函数的性质及模糊加权和的特性,定义更多的松弛矩阵变量,以达到减少保守性的目的。该方法也被称为“松弛变量法”,主要用于PDC策略的放松,特别是基于Polya定理,获得了很多有价值的结果 [53~59] 。然而,单独基于该方法减少non-PDC策略的保守性作用不大,一般都是将该方法与其他降低保守性方法相结合。
(2)定义新型李雅普诺夫函数。早期的稳定性分析主要基于普通二次李雅普诺夫函数(Common Quadratic Lyapunov Function,CQLF),然而CQLF易导致稳定性分析的保守性,一些参数依李雅普诺夫函数(Parameter-Dependent Lyapunov Functions,PDLF)被期望用来获得更加放松的结果 [63~72] 。当前,模糊李雅普诺夫函数(Fuzzy Lyapunov Function,FLF)和分段李雅普诺夫函数(Piecewise Lyapunov Function,PLF)是研究得较多的两类PDLF。
(3)定义新的控制方案,或者充分考虑隶属函数的形状信息。例如,模糊切换控制器比单一的模糊控制器更能降低保守性 [73~79] 。另外,在设计条件中,充分考虑隶属函数的形状信息,进而定义一些松弛变量,以达到减少保守性。
需要注意的是,上述三种方法并不孤立,而是可以相互结合、互相渗透的。例如,利用FLF分析连续时间一型T-S模糊系统,会出现模糊权重的微分,通过考虑模糊权重微分的上界,实际上包含隶属函数的形状信息。接下来,主要对这三种减少保守性的方法做简要回顾。
一型 T-S 模糊控制系统的稳定性分析可以追溯到 20 世纪 90 年代。Wang和Tanaka运用PDC策略和CQLF获得了一组保证闭环系统渐近稳定的充分条件 [80,81] ,该条件可以描述如下。
定理1.1
假如存在矩阵
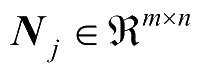 (
j
=1,2,…,
p
)及
(
j
=1,2,…,
p
)及
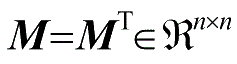 使得如下线性矩阵不等式(Linear Matrix Inequalities,LMIs)成立
使得如下线性矩阵不等式(Linear Matrix Inequalities,LMIs)成立
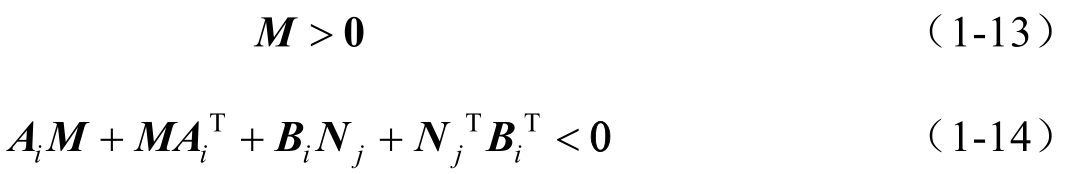
则一型T-S模糊闭环系统式(1-7)渐近稳定。其中,反馈增益矩阵可定义为
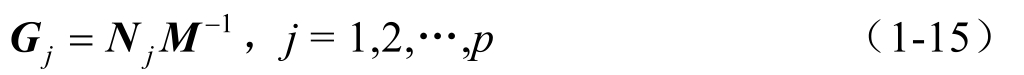
显然,文献[80,81]的结果相当保守,为了进一步减少设计条件的保守性,运用松弛变量技术,文献[53~59]获得了具有较少保守性的结果。其主要思想就是利用Polya定理,进而介绍更多的松弛变量,从而达到减少保守性的目的。
松弛变量法在一定程度上减少了设计条件的保守性,但文献[53~59]推导镇定条件时使用了CQLF,即

从式(1-16)的定义可以看出,CQLF 的时间微分在整个运行域内必须为负,这在一定程度上导致了镇定条件的保守性。因此,很多研究者尝试运用 PDLF推导模糊反馈控制器的存在条件。
FLF通过模糊权重将一些局部二次李雅普诺夫函数光滑连接,具体形式可以描述为
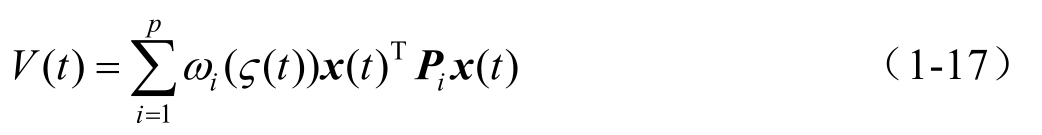
从式(1-17)可以看到,即使存在某些局部二次李雅普诺夫函数的时间微分不为负,FLF 的时间微分也可能为负。另外,CQLF 的时间微分在整个运行域内必须为负,因此,FLF比CQLF可获得更少保守性的结果。目前,基于FLF进行一型T-S模糊闭环系统的稳定性分析取得了很多有价值的成果,相关成果通过仿真实例显示了FLF比CQLF具有较少的保守性 [66~72] 。
然而,利用FLF分析连续时间一型T-S模糊系统时,FLF的时间微分将变得非常复杂,导致推导过程变得十分困难。因为对于连续时间情形,FLF的时间微分将出现前提变量微分,大多数文献都将其用上界代替。然而,很多一型T-S 模糊系统的前提变量就是系统状态,而状态变量的微分将依赖控制输入,因此估计状态变量微分的上界十分困难。为了解决该困难,文献[82]提出了一类新型的线性积分FLF,该FLF可以避免出现前提变量微分,因此可能在实际应用中扮演更重要的角色。
PLF 也是由一些局部的二次李雅普诺夫函数组成的。相对于 CQLF,PLF也具有减少保守性的潜力。目前,文献中主要存在两类 PLF,它们的主要思想都是对模糊空间进行划分,从而定义若干子空间,再在每个子空间定义局部二次李雅普诺夫函数。第一类 PLF 主要见文献[83~85]。它依据模糊权重的大小,将前提变量空间划分为 p 个子域,即
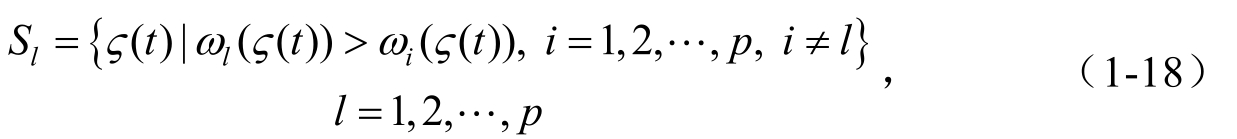
然后基于该划分方式重新描述原始的一型T-S模糊闭环系统,再使用PLF推导反馈控制器的存在条件,其PLF可定义为
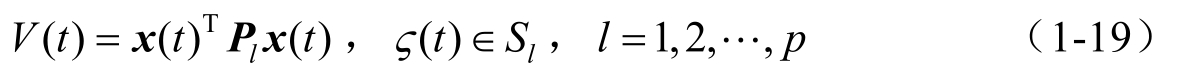
在利用第一种划分方式重新表述原始的一型T-S模糊闭环系统时,子系统之间的相互作用得到了加强。然而,子系统之间的相互作用是通过不确定项表述的。在推导镇定条件时,一般用其最坏上界处理该不确定项,这在一定程度上带来了保守性。有关第一类PLF的相关报道可参考文献[83~86]。
第二类PLF主要由文献[87]提出。它依据模糊权重的特性,将前提变量空间划分为若干子空间。首先将前提变量空间划分为两类域,分别称为清晰域和模糊域。在任意清晰域中,必存在某个
l
∈{1,2,…,
p
}有
 ,
i
≠
l
。也就是说,在清晰域中,有一个模糊权重的值恒为 1,而其他模糊权重的值恒为 0。因此在清晰域内,系统的动态可通过一个局部线性子系统表述。在模糊域中,所有的模糊权重值都满足
,
i
≠
l
。也就是说,在清晰域中,有一个模糊权重的值恒为 1,而其他模糊权重的值恒为 0。因此在清晰域内,系统的动态可通过一个局部线性子系统表述。在模糊域中,所有的模糊权重值都满足
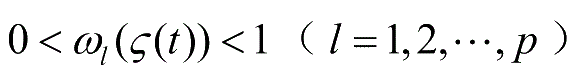 ,即系统动态是一些线性子系统的凸组合。于是,模糊域和清晰域具有不同的子模型,再在每个子域内定义局部二次李雅普诺夫函数,就可以构成形式如式(1-19)的第二类PLF。第二类PLF在实际应用中获得了不错的效果
[88~90]
。然而,它对于清晰域和模糊域不明显的一型T-S模糊系统效果不是很理想
[86]
。
,即系统动态是一些线性子系统的凸组合。于是,模糊域和清晰域具有不同的子模型,再在每个子域内定义局部二次李雅普诺夫函数,就可以构成形式如式(1-19)的第二类PLF。第二类PLF在实际应用中获得了不错的效果
[88~90]
。然而,它对于清晰域和模糊域不明显的一型T-S模糊系统效果不是很理想
[86]
。
FLF通过模糊权重将局部的二次李雅普诺夫函数光滑连接而成,类似软切换方式。从式(1-19)可知,PLF 实质上是一种硬切换,因此局部二次李雅普诺夫函数必须在每个域的边界处连续,以使全局函数是一个有效的李雅普诺夫函数。文献[87]讨论了相关问题。另外,FLF和PLF虽然比CQLF可以获得更少保守性的结果 [66~72,82~101] ,但基于FLF和PLF的推导过程会比CQLF复杂,且带来更大的计算负担。随着高性能计算机的出现,计算负担可以得到一定程度的缓解,因此本书主要致力减少设计条件的保守性。
隶属函数形状依赖(Membership Function Shape Dependent,MFSD)分析法是相对于隶属函数形状独立(Membership Function Shape Independent,MFSI)分析法而言的。MFSI 分析法不考虑隶属函数的形状信息,一旦推导的镇定条件保证了模糊闭环系统的稳定性,系统的稳定性将不受隶属函数形状的影响。明显地,MFSI 分析法容易导致保守性的结果。MFSD 分析法可将隶属函数的形状信息代入设计条件,于是MFSD分析法可能获得比MFSI分析法更少的保守性。目前,隶属函数界(Membership Function Boundary,MFB)分析法和阶梯隶属函数(Staircase Membership Function,SMF)分析法是主要的两类MFSD分析法。
MFB分析法主要考虑将模糊权重的上、下界利用在设计条件中,并运用线性矩阵不等式技术定义更多的松弛变量,从而获得更少的保守性结果。基于MFB 分析法获得的镇定条件只适用于满足界约束的特殊类模糊系统,而不适合于任何隶属函数形状的模糊系统,这在一定程度减少了设计条件的保守性。文献[30]通过考虑模糊控制器与模糊系统的模糊权重上、下界,提出了基于 LMI的镇定条件,该条件放松了文献[81]的结果。文献[31]通过考虑模糊权重的仿射界约束,提出的镇定条件比文献[30]具有更少的保守性。文献[61]研究了具有不匹配前提隶属函数的模糊闭环系统,通过考虑模糊权重的界约束及其性质,介绍了更多松弛变量,给出了反馈控制器存在的充分条件,仿真例子证实了该方法的优越性。文献[69]通过运用 FLF,并且同时考虑模糊权重微分及模糊权重的界约束,获得了基于LMI的镇定条件和性能条件。文献[102]通过考虑模糊权重的界及模糊权重乘积的界,放松了文献[55]的结果。文献[103]考虑了关于隶属函数形状的多项式约束,进而将其整合到镇定条件,数值例子表明了该方法的有效性。
前述的MFB分析法主要考虑整个运行域的界信息,这种全局信息并不能反映隶属函数的局部形状信息。所以,将运行域划分为若干子域,再在每个子域内使用 MFB 分析法,该方式可能比在整个域内直接使用 MFB 分析法更能反映隶属函数的形状信息。文献[104~107]利用隶属函数的局部形状信息,获得了较少保守性结果。文献[104]不要求模糊控制器与模糊系统分享相同的前提隶属函数和模糊规则数,通过考虑分段隶属函数的界、形状和位置,并利用李雅普诺夫稳定性理论获得了基于LMI的镇定条件。文献[105]使用多项式函数近似模糊控制与模糊系统的权重乘积项,再运用S-过程(S-procedure)获得了具有较少保守性的镇定条件。文献[106]通过采样点特征化原始的模糊权重,并在每个局部域内考虑隶属函数及其微分的界信息,再运用 FLF 给出了保证闭环系统渐近稳定的充分条件。文献[107]将整个运行域划分为若干子域,再在每个子域内考虑隶属函数的界信息,并构造了基于多维模糊和形式的不等式约束,利用不等式约束定义了少数松弛矩阵变量,从而获得了较少保守性的镇定条件。事实上,文献[108]提出的SMF分析法也在一定程度上反映隶属函数的局部信息,而不是笼统考虑隶属函数的全局形状信息,这在一定程度上减少了设计条件的保守性。SMF 分析法通过阶梯函数近似模糊系统及模糊控制器的模糊权重,将模糊权重的采样点信息考虑进了推导过程,进而获得了较少保守性结果。当阶梯函数的步长尺寸趋于零时,阶梯函数也就越加逼近原始的模糊权重。因此阶梯函数划分得越细,获得的镇定性条件越放松。
MFSD分析法比MFSI分析法能获得较少的保守性,然而MFSD分析法比MFSI分析法更加复杂,在一定程度上加剧了模糊反馈控制器设计的难度。