




考虑如下的区间二型T-S模糊系统。
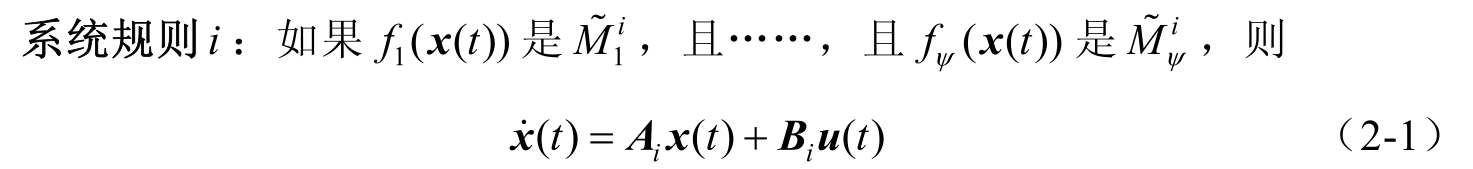
式中,
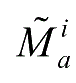 为相关于函数
f
a
(
x
(
t
))的区间二型模糊集,
a
=1,2,…,
Ψ
,
i
=1,2,…,
p
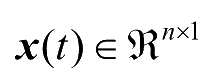
;为状态向量;
为相关于函数
f
a
(
x
(
t
))的区间二型模糊集,
a
=1,2,…,
Ψ
,
i
=1,2,…,
p
;为状态向量;
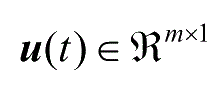 为控制输入向量。
为控制输入向量。
 第
i
条规则的激活强度可定义为如下的区间集。
第
i
条规则的激活强度可定义为如下的区间集。
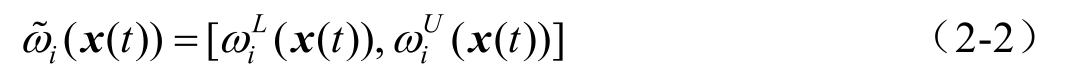
其中
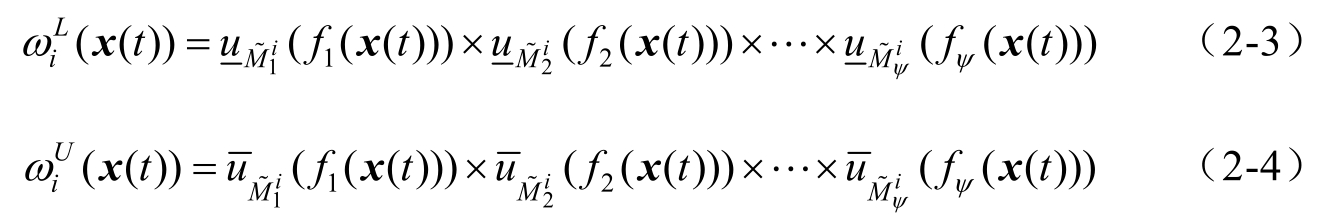
式(2-3)和式(2-4)中,
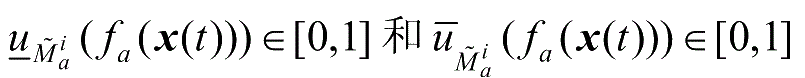 (
a
=1,2,…,
Ψ
)分别表示下、上隶属度。
(
a
=1,2,…,
Ψ
)分别表示下、上隶属度。
全局的区间二型T-S模糊模型可定义为
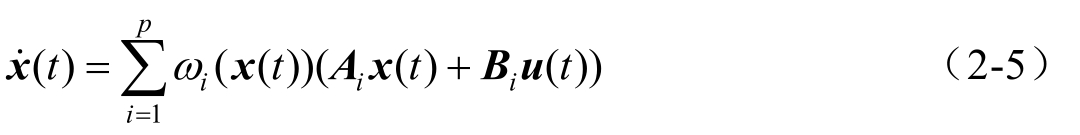
其中
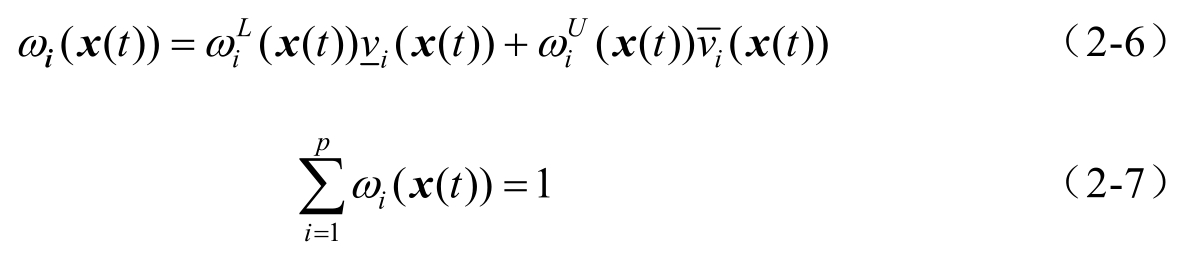
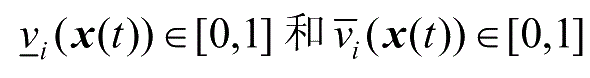 是两个非线性函数,并且满足
是两个非线性函数,并且满足
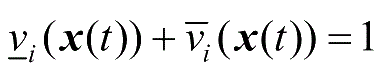 。
。
不失一般性,假设区间二型 T-S 模糊系统的运行域划分为 c 个运行子域,第 j 个区间二型模糊域值控制器的模糊规则定义如下。
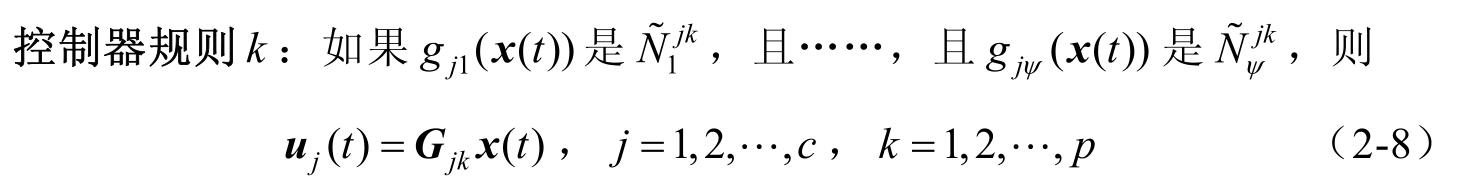
式中,
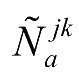 为区间二型模糊集,
a
=1,2,…,
Ψ
;
为区间二型模糊集,
a
=1,2,…,
Ψ
;
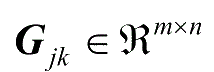 (
j
=1,2,…,
c
,
k
=1,2,…,
p
)是第
j
个模糊控制器在第
k
条规则下的反馈增益矩阵。类似文献[32]的合成规则,第
j
个区间二型模糊域值控制器可定义为
(
j
=1,2,…,
c
,
k
=1,2,…,
p
)是第
j
个模糊控制器在第
k
条规则下的反馈增益矩阵。类似文献[32]的合成规则,第
j
个区间二型模糊域值控制器可定义为
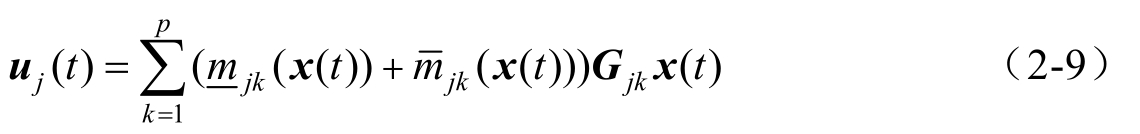
其中
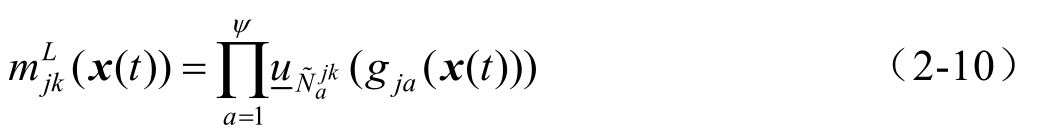
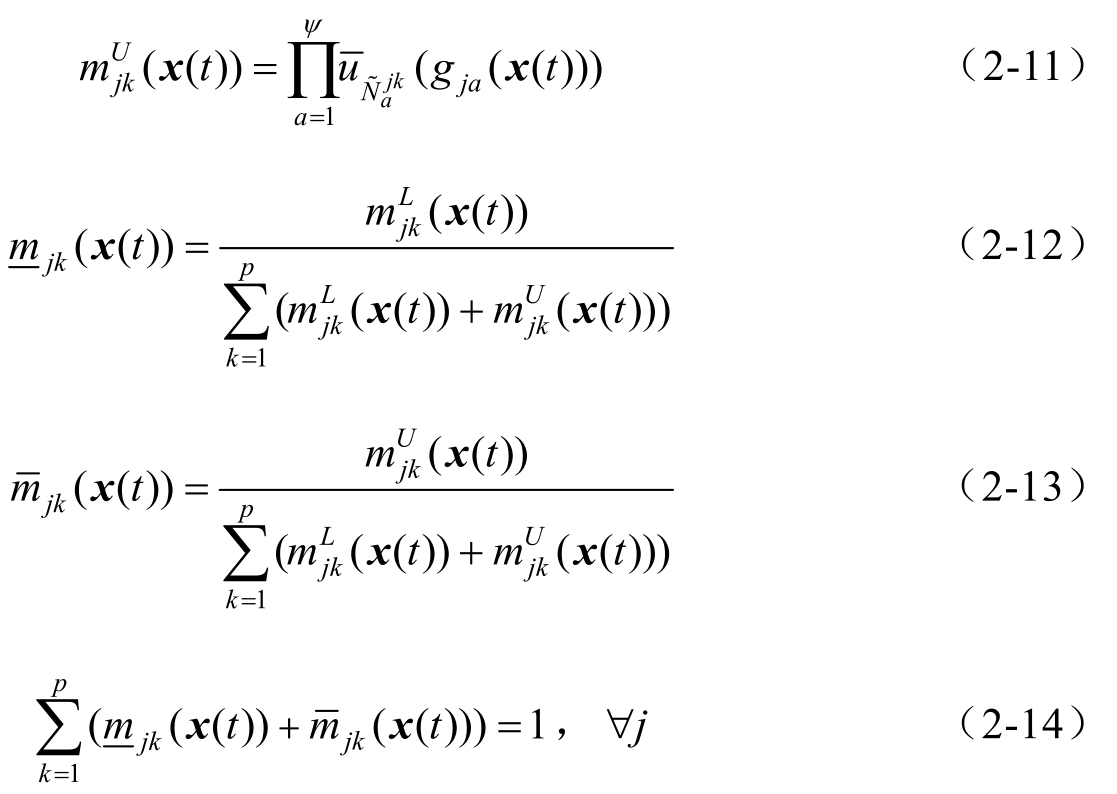
接下来,定义一个决策变量
v
j
(
x
(
t
))∈{0,1}。如果系统状态处在第
j
个运行子域内,则
v
j
(
x
(
t
))=1,否则
v
j
(
x
(
t
))=0。由于没有重叠的子域,
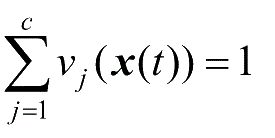 必定满足。由式(2-9),全局的区间二型模糊域值切换控制器可定义为
必定满足。由式(2-9),全局的区间二型模糊域值切换控制器可定义为
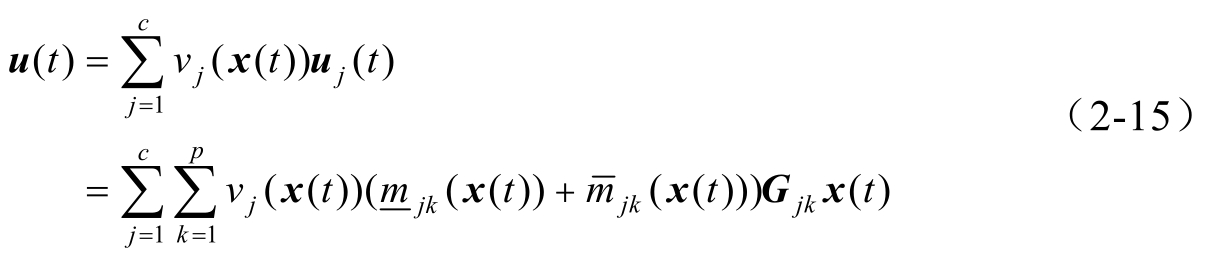
为了方便,在本章的后文中,
ω
i
(
x
(
t
))、
v
j
(
x
(
t
))、
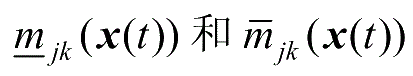 分别表示为
i
ω
、
v
j
、
m
jk
和
分别表示为
i
ω
、
v
j
、
m
jk
和
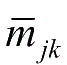 ,因此,由式(2-5)和式(2-15)形成的闭环系统可表示为
,因此,由式(2-5)和式(2-15)形成的闭环系统可表示为
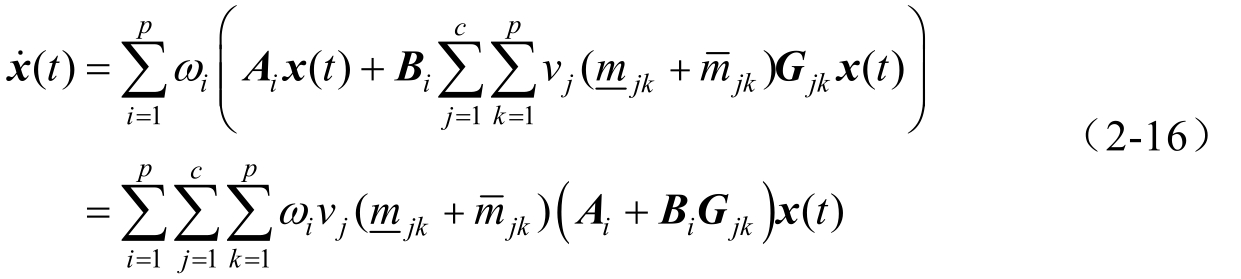
本章的目的就是找到反馈增益 G jk ,使得闭环系统式(2-16)渐近稳定。