





首先从第1章凝炼出“安全”的几个更具体的概念,以便本章直接使用。
安全是一个很主观的概念,与角度密切相关。同一个事件,对不同的人、从不同的角度来说可能会得出完全相反的安全结论。比如,“政府监听嫌犯通信”这件事,从政府角度来看,“能监听”就是安全;而对嫌犯来说,“能监听”就是不安全。所以,下文研究安全,只锁定一个角度,如“我”的角度,即某个行为结果到底是安全还是不安全,完全由“我”说了算,别人无权干涉。当然,这里的“我”,可能是一个人,也可能是一个机构,还可能是一群人,但是,要求他们在所处理事件上的观点是一致的(当然,在其他不相关的事件上,他们的态度完全可以各不相同)。
安全是一个与时间密切相关的概念。同一个系统,昨天安全绝不等于今天也安全(比如,若用现代计算机去破译古代密码,简直是易如反掌)。同样,今天安全也绝不等于明天就安全。当然,一个“昨天不安全”的系统,今天也不会自动变为安全。因此,本章研究安全时,只考虑时间正序流动的情况,更严格地说,只考虑当前时刻的安全情况。
安全是一个与对象密切相关的概念。假设A和B是两个相互独立的系统,若只考虑A系统的安全,那么B系统是否安全就应该完全忽略。比如,若只考虑“我的手机是否安全”,那么“远方登山者是否安全”就可以完全忽略。因此,本章研究安全时,就只锁定一个有限系统,即该系统由有限个“元件”组成。由于本书的研究对象(人类的网络空间系统)无论多么巨大,永远都只是有限系统,所以网络空间中的任何部分就更是有限系统了。
考虑系统A,如果直接研究其安全,那么根本就无处下手!不过,幸好有“安全”=不“不安全”,所以,若能够把“不安全”研究清楚了,那么“安全”也就明白了。从理论上来说,有限系统的不安全事件也是有限的。为了便于理解,建议读者将本章研究的系统想象为计算机网络。
下面就以概率论为工具,从“我”的角度,沿着时间的正序方向(但只考虑当前状态)来研究系统A的“不安全”。特别说明:本书概率一般用 P 表示,有的地方为了与变量 P 和 p 区别,用 P r 表示了概率。
假定A系统中发生了某个事件,如果它是一个对“我”来说的不安全事件,那么“我”就能够精确且权威地判断这是一个不安全的事件,因为该事件的后果是“我”不愿意接受的。(注意:除“我”之外,别人的判断是没有参考价值的,因为此处只从一个角度来研究安全。)如果将该不安全事件记为 D ,那么该事件导致系统A不安全的概率就记为 P ( D )。为了简化计,我们只考虑0< P ( D )<1的情况,因为如果 P ( D )=0,那么这个不安全事件 D 就几乎不会发生,故可以忽略,因为无论是否对造成事件 D 的环境进行安全加固,都不影响系统A的安全性;如果 P ( D )=1,那么 D 就是不安全的确定原因(几乎没有随机性),这时只需要针对事件 D 单独进行安全加固(如采用现在所有可能的已知安全技术手段。实际上,当前全球信息安全界都擅长于这种“头痛医头,足痛医足”的方法),就可以提升系统A的安全性。
从理论上看,给定系统A之后,如果A是有限系统,那么总可以通过各种手段发现或测试出当前的全部有限个不安全事件,如 D 1 , D 2 ,…, D n 。下面在不引起混淆的情况下,用 D i 同时表示不安全事件和造成该事件 D i 的原因。于是,系统A的“不安全”概率就等于 P ( D 1 ∪ D 2 ∪…∪ D n ),或者说,系统A的“安全”概率等于1- P ( D 1 ∪ D 2 ∪…∪ D n )。
换句话说,本来无处下手的安全研究,就转化为下面的数学问题:在概率0< P ( D 1 ∪ D 2 ∪…∪ D n )<1的情况下,使 P ( D 1 ∪ D 2 ∪…∪ D n )(即不安全的概率)最小化的问题,或者使1- P ( D 1 ∪ D 2 ∪…∪ D n )(即安全的概率)最大化的问题。
设 D 和 B 是系统A的两个不安全事件,那么( D ∪ B )也是一个不安全事件,但是( D ∩ B )或( D \ B )等就不一定再是不安全事件了。(特别提醒:这里的“事件”是集合论中的术语,所以,集合 D ∩ B 意指集合 D 和 B 相交的那部分子集,当然它也就不一定再是不安全事件了;与此类似, D \ B 也不一定再是不安全事件了。)若事件 D 是 B 的真子集,并且 D 的发生会促使 B 也发生(即条件概率 P ( B │ D )> P ( B )),则称事件 D 是事件 B 的子事件。
在时间正序流动的条件下,设系统A过去全部的不安全事件集合为 D ,若当前又发现一个新的不安全事件 B ,那么系统A的当前不安全概率= P ( D ∪ B )≥ P ( D )=系统A的过去不安全概率。于是,便有不安全性遵从热力学第二定律:系统A的不安全概率将越来越大,而不会越来越小(除非有外力,如采取了相应的安全加固措施等),所以“不安全”是熵,或者说“安全”是负熵。
热力学第二定律说:热量可以自发地从高温物体传递到低温物体,但不可能自发地从低温物体传递到高温物体;热量将最终稳定在温度一致的状态。那么,有限系统A的不安全状态将最终稳定在什么地方呢?下面就来回答这个问题。
设 Z 是一个不安全事件,如果存在另外两个不安全事件 X 和 Y (它们都是 Z 的真子集),同时满足以下两个条件:
(1) X ∩ Y =∅(空集)
(2) Z = X ∪ Y
那么,就说不安全事件 Z 是可分解的。此时 X 和 Y 都是 Z 的子事件。如果某个不安全事件是不可分解的(即它的所有真子集都不再是不安全事件),那么就称该事件为不安全的素事件。
定理2.1(不安全事件分解定理):对任意给定的不安全事件 D ,都可以判断出 D 是否是可分解的,并且,如果 D 是可分解的,那么也可以找到它的某种分解。
证明:由于有限系统A的全部不安全事件只有有限个 D 1 , D 2 ,…, D n ,所以至少可以通过穷举法对每个 D i ( i =1,2,…, n )测试一下 D \ D i ,看它是否也是不安全事件。如果至少能够找到一个这样的 i ,那么 D 就是可分解的,而且, D i 与( D \ D i )就是它的一个分解;否则,如果这样的 i 不存在,那么 D 就是不可分解的不安全素事件。这是因为 D 1 , D 2 ,…, D n 是全部不安全事件。证毕。
定理2.2(不安全事件素分解定理):若反复使用上述的不安全事件分解定理(定理2.1)来处理不安全事件( D 1 ∪ D 2 ∪…∪ D n )及其被分解后的不安全子事件,那么就可以最终得到分解
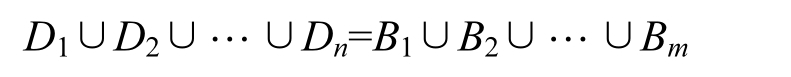
这里,对任意 i 和 j ( i , j =1,2,…, m )都有 B i 是不安全素事件,并且当 i ≠ j 时, B i ∩ B j =∅。
证明:若 D = D 1 ∪ D 2 ∪…∪ D n 已经是不可分解的,那么 m =1,并且 D 1 ∪ D 2 ∪…∪ D n = B 1 。
若 D 是可以分解的,并且 X 是 D 分解后的一个不安全子事件,如果 X 已经不可分解,那么可以取 B 1 = X ;如果 X 还可以再分解,那么再对 X 的某个不安全子事件进行分解。如此反复,直到最终找到一个不能再被分解的不安全子事件,将该事件记为 B 1 。
仿照上面分解 D 的过程来分解 D \ B 1 ,便可以找出不能再被分解的不安全子事件 B 2 。
再根据 D \( B 1 ∪ B 2 )的分解,便可得到 B 3 。
最终,当这个分解过程结束后,全部 B i 就已经构造出来了。证毕。
于是,根据定理2.2,当 i ≠ j 时,便有 B i ∩ B j =∅,并且有
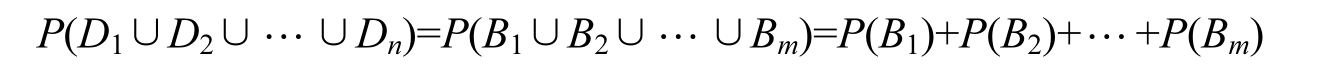
因此,可以将引发有限系统A的不安全事件 D 1 , D 2 ,…, D n 分解为另一批彼此互不相容的不安全素事件 B 1 , B 2 ,…, B m ,并且还将有限系统A的不安全概率转化为 P ( B 1 )+ P ( B 2 )+…+ P ( B m )。所以,有限系统A的不安全概率 P ( D 1 ∪ D 2 ∪…∪ D n )的最小化问题,也就转化成了每个彼此互不相容的不安全素事件的概率 P ( B i )( i =1,2,…, m )的最小化问题。换句话说,我们有如下结果。
定理2.3(分而治之定理):任何有限系统A的不安全事件集合都可以分解成若干个彼此互不相容的不安全素事件 B 1 , B 2 ,…, B m ,使得只需要对每个 B i ( i =1,2,…, m )进行独立加固,即减小事件 B i 发生的概率 P ( B i ),就可以整体上提高系统A的安全强度,或者说整体上减小系统A的不安全概率。
定理2.3回答了前面的“热平衡”问题,即有限系统A的不安全状态将最终稳定成一些彼此互不相容的不安全素事件之并集。该定理对网络空间安全界的启发意义在于:过去那种“头痛医头,足痛医足”的做法虽然值得改进,但也不能盲目地“头痛医足”或“足痛医头”,而应该科学地将所有安全威胁因素分解成互不相容的一些“专科”( B 1 , B 2 ,…, B m ),然后再开设若干“专科医院”来集中精力“医治”相应的病症,即减小 P ( B i )。
专科医院也是要细分科室的,同样,针对上述的每个不安全素事件 B i 也可以再进一步进行分解,并最终得到系统A的完整“经络图”,于是便找到了某些“头痛医足”的依据,甚至给出“头痛医足”的办法。