下载掌阅APP，畅读海量书库
立即打开
为了说明另一种形式的能量，我们来考虑一个单摆（图4-7）。假如我们把它拉向一边，再把它放开，它就会来回摆动。在这种运动中，每当从端点跑向中点时，它的高度降低了，这时势能跑到哪里去了呢？当摆降到底部时，势能就消失了，不过，它将再次爬上来。可见重力势能必定转变为另一种能量形式。很明显它是依靠了自己的 运动 才能重新爬上来的。所以，当它到达底部时，重力势能就转变为某种其他形式的能量。
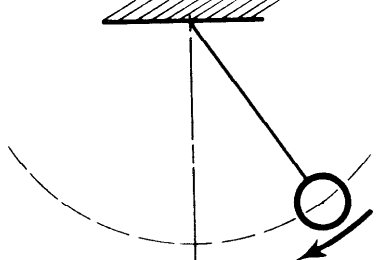
图4-7 单摆
我们应当得出一个运动能量的公式。现在，回想一下关于可逆机的论证，很容易看出，在底部的运动必定具有一定量的能量，可使摆升高到一定高度，这个能量与摆上升的 机制 无关，或者说与上升的路径无关，所以与我们对孩子玩积木的情形所写出的公式一样，这里也有一个（两种能量间的）等价公式。我们有另一种表示能量的形式，要说明它是不难的。摆在底部的动能等于重量乘以它能升高的高度：K．E．＝ W · H 。现在需要的是一个利用某种与物体的运动有关的规则来说明摆动高度的公式。假如我们以一定的速度直接朝上抛出一个物体，它将到达一定的高度。我们暂时还不知道到底是多高，但是它依赖于速度——关于这个，有一个相应的公式。于是，为了找到物体以速度 V 运动的动能的公式，我们必须计算它能到达的高度，再乘以物体的重量。我们立刻就会知道，可以把动能写成这种形式
K．E．＝ WV 2 ／（2 g ）．（4．6）
当然，运动具有能量这个事实与物体处于重力场内这件事毫无关系。无论运动怎样产生，这都没有关系。这是一个适用于各种速度的一般公式。式（4．3）及式（4．6）都是近似的公式。式（4．3）在高度很大时是不正确的，因为这时，重力要减弱，而式（4．6）在高速时要加以相对论性的校正。然而，当我们最后得到动能的精确公式时，能量守恒定律则是正确的。