




算法时间复杂度分析是评估算法优劣的一个重要指标,同时算法时间复杂度分析和执行时间的测试也是一个学习难点。本节在1. 2节的基础上拓展介绍相关分析和计算的技巧。
分析算法时间复杂度的一般步骤如图1-15所示。
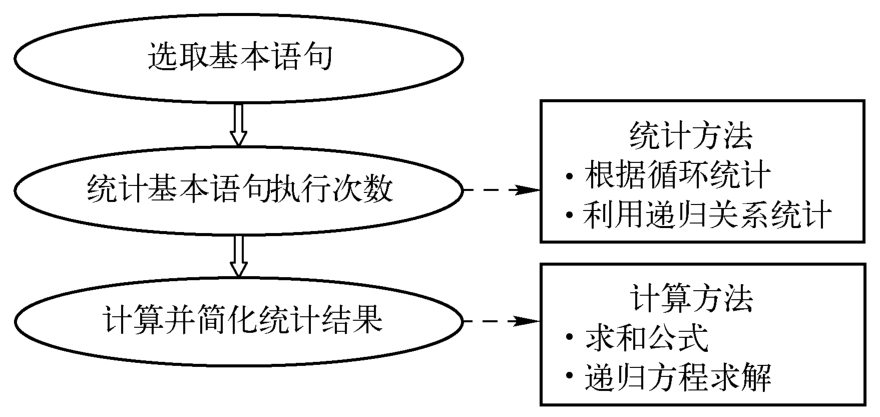
图1-15 算法时间复杂度分析的一般步骤
根据循环统计基本语句的执行次数这种算法时间复杂度的分析方法已在1.1.3节中进行了介绍。对于一个递归算法又该如何分析时间复杂度呢?
递归算法的分析方法比较多,常用的是迭代法。迭代法的基本步骤是先将递归算法简化为对应的递归方程,然后通过反复迭代,将递归方程的右端变换成一个级数,最后求级数的和,再估计和的渐进阶。
【 例1-1 】递归求 n !的算法如下,试分析其算法时间复杂度。

分析:
算法的递归方程为 T ( n )= T ( n -1)+ O (1)
迭代展开:
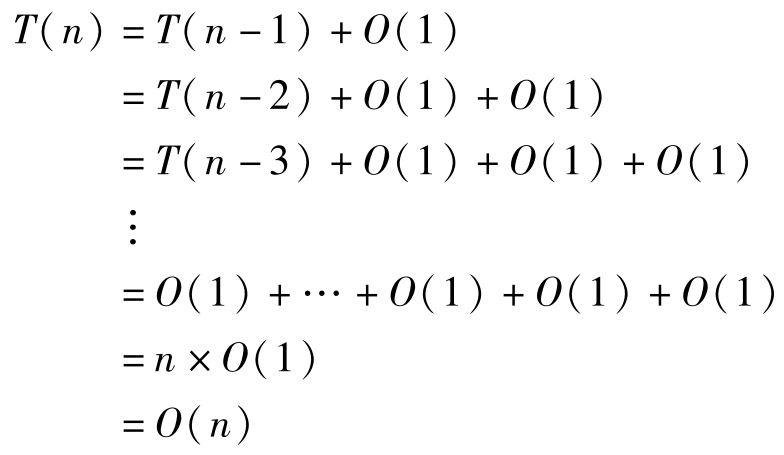
因此,该递归算法的时间复杂性是线性的。
说明:递归方程的计算除了迭代法之外,还有代换法、递归树法、主定理法等,读者可阅读相关参考书籍进一步了解。
【 例1-2 】计算下列程序段的时间复杂度。

分析:
循环语句while(s<n) s+= ++i;
等价于while(s<n){i=i+1;s+=i;}
显然 i 每次增加1,循环体就执行一次,执行过程如下:
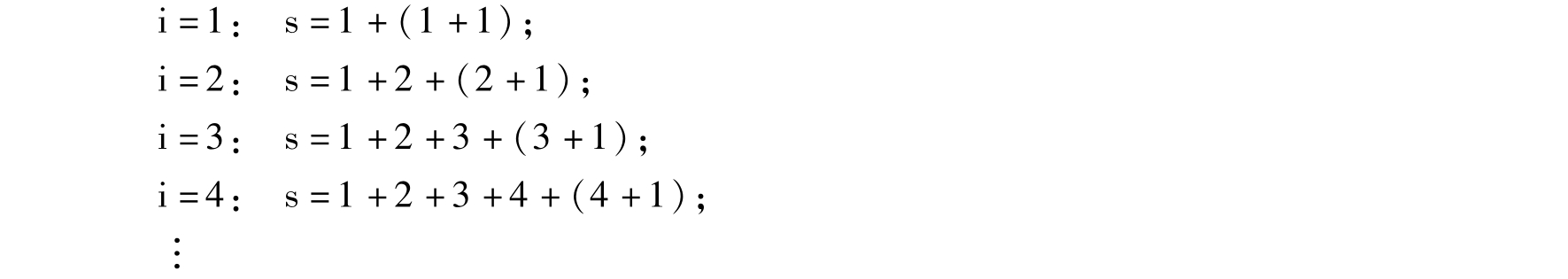
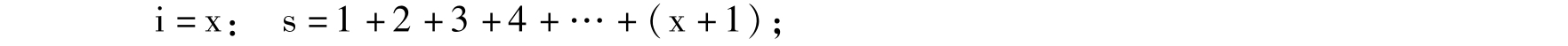
因此,满足1+2+3+4+…+(x+1)≥n的最小
x
值即为循环体执行的次数。显然此时
x
是
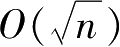 数量级的,因此时间复杂度是
数量级的,因此时间复杂度是
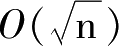 。
。
【 例1-3 】计算下列程序段的时间复杂度。

分析:
观察 i 的变化规律:3 1 ,3 2 ,3 3 ,3 4 …
设循环体共执行 x 次,则:3 x ≤ n ,解得: x ≤log 3 n 。
说明 x 从1到log 3 n 共执行了log 3 n 次,因此该程序段的时间复杂度为 O (log 3 n )。
【 例1-4 】假设 n 是3的倍数,计算下列程序段的时间复杂度。

分析:
基本语句
y
+=
i
*
j
;的执行次数为
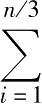 (
n
-3*
i
+1)=(
n
-2)+(
n
-5)+…+4+1=
(
n
-3*
i
+1)=(
n
-2)+(
n
-5)+…+4+1=
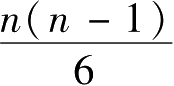 ,因此,这段代码的时间复杂度为
O
(
n
2
)。
,因此,这段代码的时间复杂度为
O
(
n
2
)。
【 例1-5 】计算下列程序段的时间复杂度。

分析:
该程序段是双重循环,着重考虑双重循环内循环体基本语句s=s+a[i][j];执行的次数。
观察外层循环变量 i 的变化规律:2 1 ,2 2 ,2 3 ,2 4 ,…参照例1-3的方法,可知外层循环执行了log 2 n 次;再考察外层循环变量 j 的变化规律:1,2,3,4,…共执行了 n 次。基本语句s=s+a[i][j];执行的次数=外层循环执行次数×内层循环执行次数= n log 2 n 。
因此,该程序段的时间复杂度为 O ( n log 2 n )。
1.1.3节中介绍了利用渐进时间复杂度这种事前分析估算的方法来分析算法的效率。本节将介绍利用后期测试法来分析算法效率。
不同算法用计算机程序实现后,其执行时间也不尽相同。算法执行时间的精确测试对算法执行效率的分析和评价也有着重要的意义。
测试算法执行时间的常规方法如下:在待测试的算法代码片段前,创建一个变量记录当前的系统时间;待算法代码片段执行完成后,用另一个变量记录新的时间;二者之差即为算法代码片段的执行时间。算法执行时间的测试流程如图1-16所示。
图1-16 算法执行时间的测试流程
实例代码如下:

说明:CLOCKS_PER_SEC是time. h头文件中宏定义的一个常数,用于将clock()函数的结果转化为以秒为单位的量。
目前的PC操作系统都是支持多任务的,操作系统分配时间片(Time slice)给每个任务轮流使用CPU。在多任务操作系统下,使用本节介绍的常规时间测试方法检测算法代码片段执行时间所得的结果为算法在计算机上的运行时间,而不是算法在CPU的执行时间,测得的时间比算法实际的执行时间大,并不是精确的结果。不过,这种常规测试方法用于在同一计算机环境下对多个算法进行时间性能比较还是可行的。