




本节运用1. 1节所学知识来分析导学问题1中涉及的数据结构以及计算导学问题2的时间复杂度。
对于导学问题1-4、1-5和1-6这几个比较复杂的问题,先对其抽象出数学模型。
如图1-11所示,在问题1-4中的学生成绩表中,每个学生的学号、姓名、某门课程的成绩称为数据项,每个学生包含这些数据项的记录称为数据元素。所有数据元素(这个班级的学生)的集合就构成了一个数据对象。
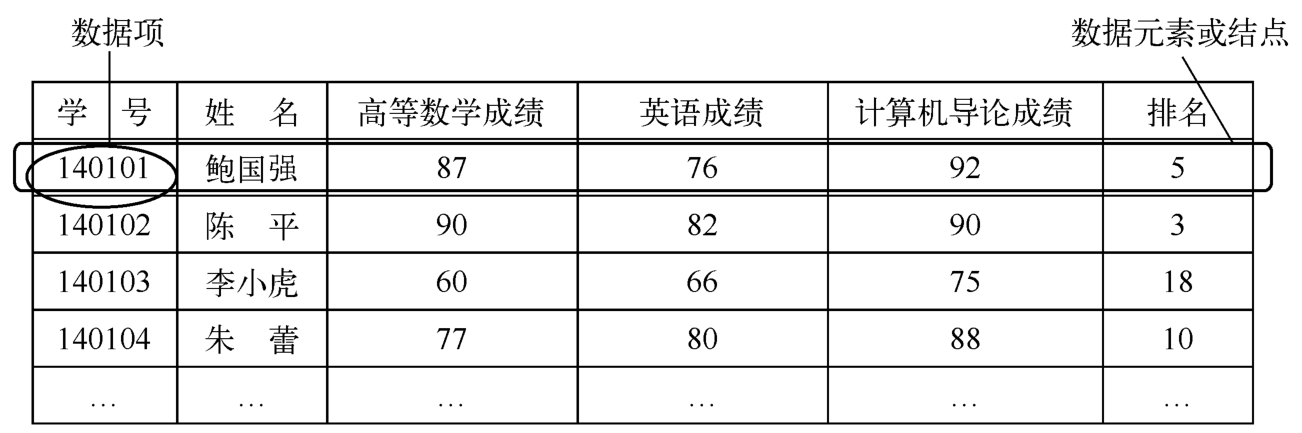
图1-11 学生成绩表中的数据项、数据元素
将每一个数据元素看作一个结点,用圆圈表示,元素之间的逻辑关系用结点之间的连线表示,则问题就可以抽象成如图1-12所示的一对一的线性逻辑结构。

图1-12 线性逻辑结构
在问题1-5中,把Linux系统中的文件、文件夹称为数据元素,将每一个数据元素看作一个结点,用圆圈表示,元素之间的逻辑关系用结点之间的连线表示,则问题中的数据元素之间的关系就可以抽象成如图1-13所示的树形逻辑结构。本书将在第6章介绍“树”这种抽象结构的存储和操作实现。
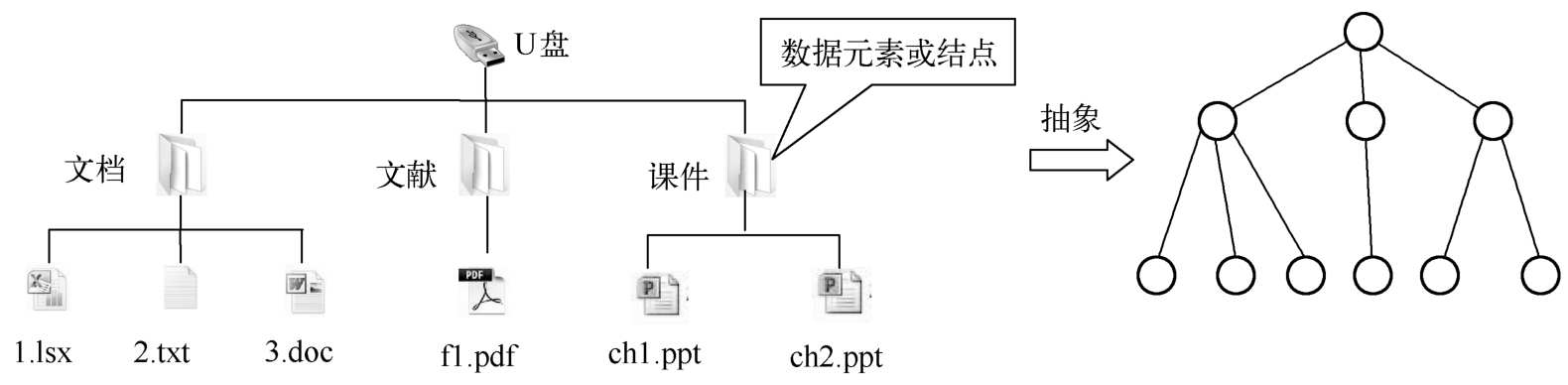
图1-13 树结构
在问题1-6中,数据元素之间的关系可以抽象成如图1-14所示的图结构。本书将在第7章介绍“图”这种抽象结构的存储和操作实现。
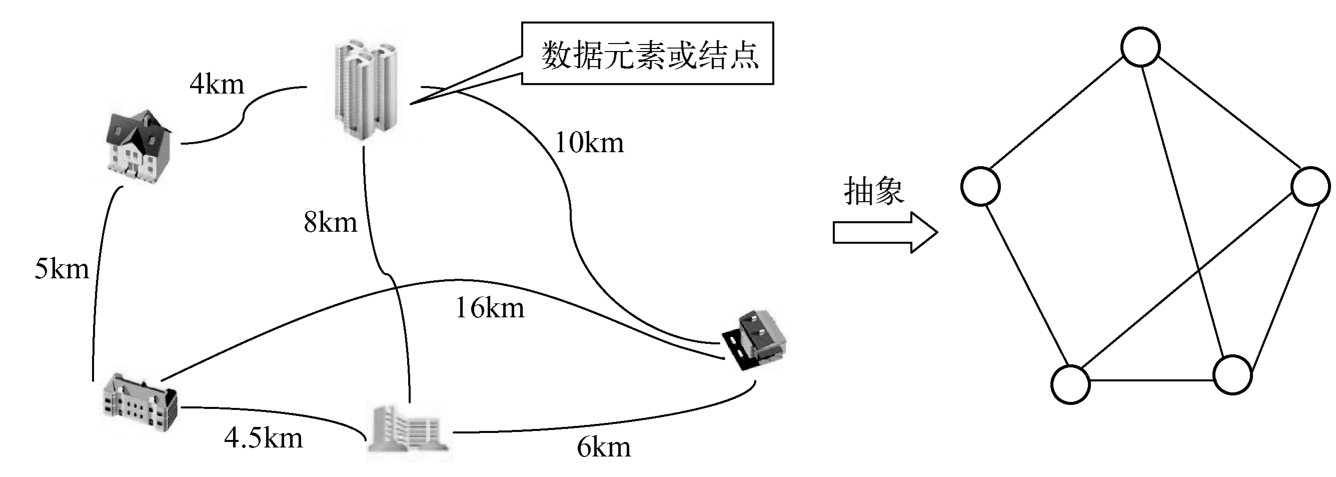
图1-14 图结构
由于循环语句的执行时间主要取决于循环体执行的次数,因此在分析循环语句时间复杂度时,更多关注的是循环体中基本语句执行的次数。
导学问题2的原始程序是一个双重循环,其中外循环体中的语句p=1,执行次数为 n ;外循环体中的语句s+=p,执行次数为 n ;内循环体中语句p*=j,执行次数为1+2+3+…+ n = n ( n +1)/2;因此该程序的基本语句执行次数是 n 2 数量级,时间复杂度 T ( n )= O ( n 2 )。
改进后的程序是一个单重循环,循环体中的语句p*=j;和s+=p;分别执行了 n 次,因此该程序的基本语句执行次数是 n 数量级,时间复杂度 T ( n )= O ( n )。
显然,改进后的程序在时间复杂度上要比初始的程序好。