




如果说情景分析和决策树是能帮助我们估计离散型风险影响的技术,那么模拟法则提供了一种监测持续型风险影响的方法。当我们在现实世界中面对的大多数风险可以带来数百个可能结果时,模拟技术能让我们更全面地认识一笔资产或投资的风险。
不同于在离散情景下认识价值的情景分析,模拟法可以让我们更灵活地应对不确定性。在经典的模拟技术中,我们需要为估值中的每个参数(增长率、市场份额、营业利润率和贝塔系数)估计出一个价值分布区间。在每次模拟中,我们从每个分布区间得到一个结果,以生成唯一一组现金流和估值结果。通过大量的模拟,我们可以推导出投资或资产的价值分布区间,以反映我们在估计投资价值时所面临的潜在不确定性。使用模拟法的具体的步骤如下所示。
(1)确定按“概率”分布的变量。 任何分析都有可能涉及数十个参数,其中某些参数是可预测的,某些则是无法预测的。与变量数可变且潜在结果数量较少的情景分析和决策树不同,在模拟法中,对可变的变量数量是不设限制的。至少在理论上,我们可以为估值中的每个参数确定一个概率分布。但实际情况是,这样做不仅需要耗费大量时间,并且有可能无法提供有价值的结果,尤其是对于那些对价值仅存在边际影响的投入。因此,我们有必要将关注点集中于那些仅对价值有重大影响的变量。
(2)确定这些变量的概率分布区间。 这是模拟分析中最关键,也是最困难的一步。一般来说,我们可以通过三种方式定义变量的概率分布:
· 历史数据 :对拥有较长历史且历史数据较为可靠的变量,我们可以使用历史数据建立该变量的分布区间。例如,假设我们试图建立长期国债利率预期变化的概率分布(用作投资分析的输入参数)。按照国债利率在1928~2016年的各年度变化情况,我们可以使用如图3-6所示的柱状图反映国债利率未来变化的分布区间。
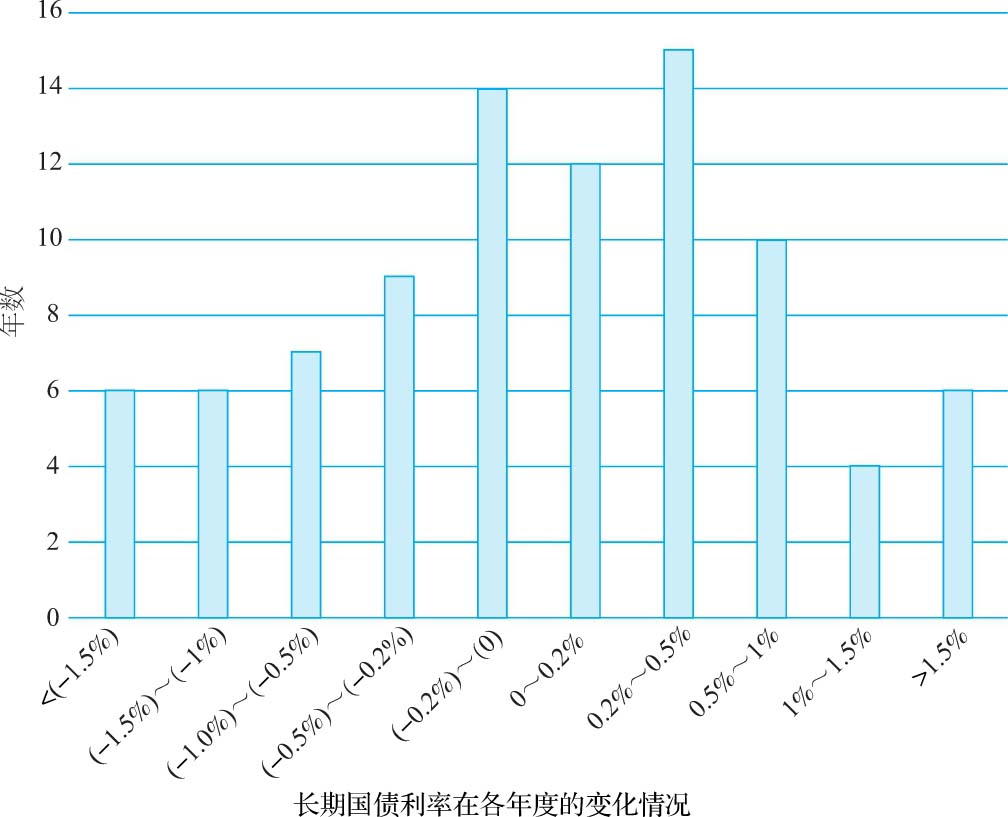
图3-6 国库券利率在1928~2016年的变化情况
这种方法隐含的假设是,市场上不存在任何会导致历史数据不可靠的结构性变化。
· 横断面数据 :在某些情况下,我们可以寻找与被分析投资相似的现有投资,以可比投资特定变量的分布来替代被分析投资相关变量的分布。我们考虑如下两个例子。假设你准备对一家软件公司估值,最让你担心的这家公司营业利润率的波动。图3-7显示了所有软件公司在2016年的税前营业利润率分布情况。
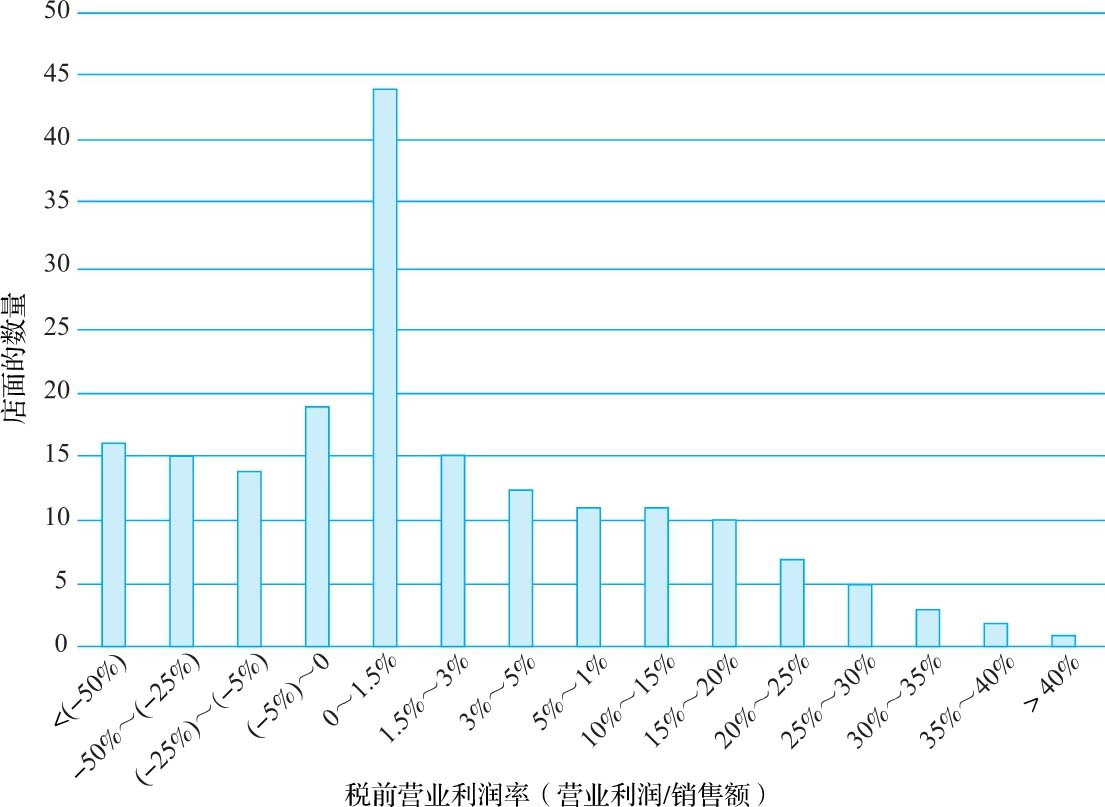
图3-7 2016年1月全美软件企业的税前经营利润率
如果采用这种分布,我们实际上就相当于假设所有软件公司营业利润率的基本分布都是相同的。在第二个例子中,假设你就职于零售商塔吉特百货,你的任务是估算新建店面投资的每平方英尺
 销售额。然后,塔吉特百货将把你得到的该变量分布运用于目前所有店面,作为模拟新商店销售额的基础。
销售额。然后,塔吉特百货将把你得到的该变量分布运用于目前所有店面,作为模拟新商店销售额的基础。
· 统计分布和参数 :对于我们打算预测的大多数变量,历史数据和横截面数据都是不足或是不可靠的。在这些情况下,我们必须选择一个最能体现输入变量波动规律的统计分布,并估计该分布的各项参数。为此,我们可以得出结论:营业利润率将在4%~8%均匀分布。此外,我们也可以认为:收入增长率服从正态分布,预期值为8%,标准差为6%。目前,很多标准的模拟软件包均可提供大量的分布函数,但选择适当的分布函数和相关参数仍很困难,原因来自两个方面。第一,在实践中,我们很少看到能满足统计分布要求的输入参数。例如,以百分比表示的收入增长率并不符合正态分布,因为它的最低值有可能是-100%。因此,我们必须找到与实际分布非常接近的统计分布函数,以确保误差不会严重颠覆我们的结论。第二,在选择分布函数后,仍需要估计相应的参数。为此,我们可以利用历史或横断面数据。对于反映收入增长的参数,我们可以分析前几年的收入增长情况,或是同业企业之间的收入增长差异。在这里,同样需要提醒的是,结构性变化会导致历史数据不可靠,同业企业之间不具备可比性。概率分布对某些输入参数可能是离散性的,而对其他参数则有可能是连续的,有些分布可以依赖于历史数据,而有些则可以依赖于统计分布。
(3)检验变量间的相关性 。虽然在指定分布后,我们会急于运行模拟,但需要提醒的是,一定要检验各变量之间的相关性。比如说,假设你准备创建利率和通货膨胀率的概率分布,尽管这两个参数在估值过程中都很关键,但它们很可能是高度相关的;高通货膨胀率往往伴随着高利率。当参数之间高度相关(正相关或负相关)时,你可以有两种选择:一种是只选择两个参数中的一个作为变量,这就要求选择对价值影响较大的那个参数;另一种是将相关性明确纳入模拟中,这需要更复杂的模拟软件包,而且需要为估算过程提供更多的细节。
(4)运行模拟。 对首次进行的模拟,我们可以从每个分布中得到一个结果,并根据这些结果进行估值。尽管随着模拟次数的增加,每次模拟对最终估值结果的边际贡献会不断下降,但我们可以按照需要多次重复这个过程。运行的模拟次数应取决于以下因素:
· 概率型输入变量的数量 :拥有概率分布特征的输入变量数量越多,所需要的模拟次数越多。
· 概率分布的特征 :被分析的分布函数越多样化,所需要模拟的次数越多。因此,和部分参数服从正态分布、部分参数采用历史数据分布特征以及部分参数服从离散分布规律的模拟相比,所有参数均服从正态分布的模拟显然需要较少的模拟次数。
· 结果的分布范围 :每个输入变量的潜在结果分布范围越大,所需要的模拟次数就越多。大多数模拟软件包都可以让用户运行数千次模拟,而且只需很少甚至不增加任何额外成本,即可增加模拟的运行次数。考虑到这个因素,宁缺毋滥或许是最好的选择。
要建立有效的模拟往往需要克服两个障碍:首先是信息障碍,将每个输入参数的价值分布纳入估值中绝非易事。换句话说,将未来5年的收入预期增长率估计为8%,显然要比为收入指定预期增长率(包括分布的类型和相关参数)要容易得多。其次是计算上的障碍。在个人计算机出现之前,模拟往往需要耗用分析师大量的时间和资源。近年来,随着这两方面的制约有所缓解,模拟技术也正在趋于普及。
在第2章中,我们采用常规型的折现现金流模型对3M公司进行了估值。我们以风险调整后的利率对预期现金流进行折现,得到每股价值86.95美元的估值结果。然而,在这个过程中,我们确实也采取了一些假设,这些假设不仅涉及公司会如何随着时间的推移发展,还包括未来的无风险利率和风险溢价等。为了对3M公司进行模拟估值,我们将做出以下假设:
· 股权风险溢价 :在基本情境下的估值中,我们使用了4%的股权风险溢价,它是标准普尔500指数在1960~2007年内在溢价的历史平均值,但这个估计值本身即存在一定的误差。因此,我们假设3M公司的股权风险溢价服从正态分布,预期值为4%,标准差为0.80%,如图3-8所示。
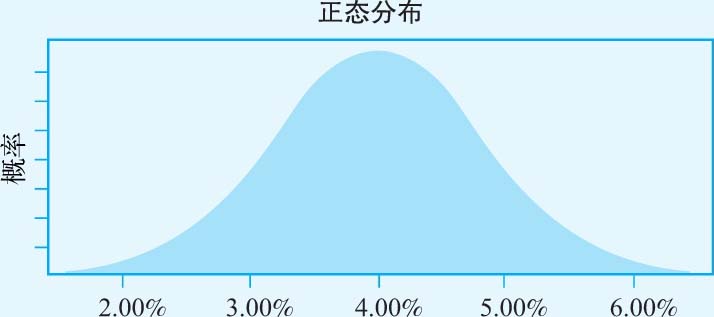
图3-8 股权风险溢价的分布规律
· 增长期的时间跨度 :我们假设3M公司将继续按高于经济增长率的水平在未来5年保持增长。为反映这个估计值的不确定性,我们将增长期的跨度设定为2~8年,且每个增长率均对应于相同的概率(见图3-9)。
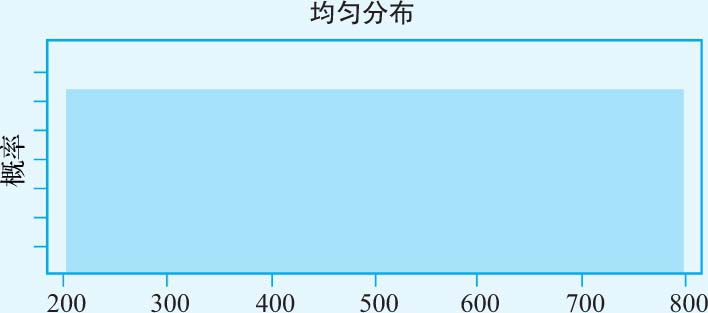
图3-9 增长期时间跨度的分布规律
· 资本收益率 :在对3M公司进行估值时,决定价值的一个关键要素就是假设公司能在未来5年内维持现有的资本收益率(约25%)。由于资本收益率会随着时间的推移和竞争的加剧而发生变化,因此我们假设资本收益率的分布规律可表示为如图3-10所示的分布。
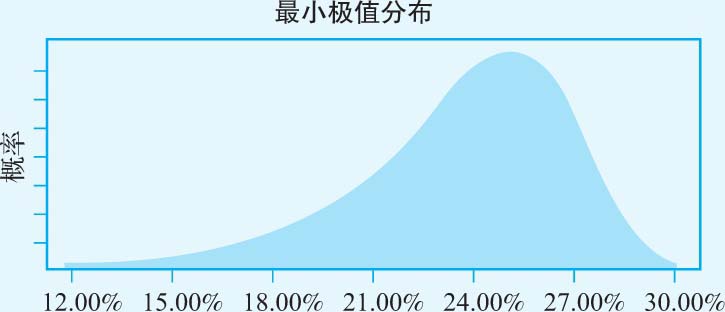
图3-10 投资资本收益率的分布规律
请注意,虽然我们假设预期的资本收益率为25%,但收益最高不能超过30%,而且未来几年的收益率可能会低得多。为此,我们可以通过该板块全部公司的资本收益率分布特征来获得3M公司的分布规律。
· 再投资率 :在基本情境下的估值中,我们假设基于历史记录,3M公司将在未来5年内保持30%的再投资率,但公司可能会提高或降低再投资率。以3M公司以往的再投资率标准差为标准,我们假设公司的再投资率服从正态分布,预期值为30%,标准差为5%,如图3-11所示。
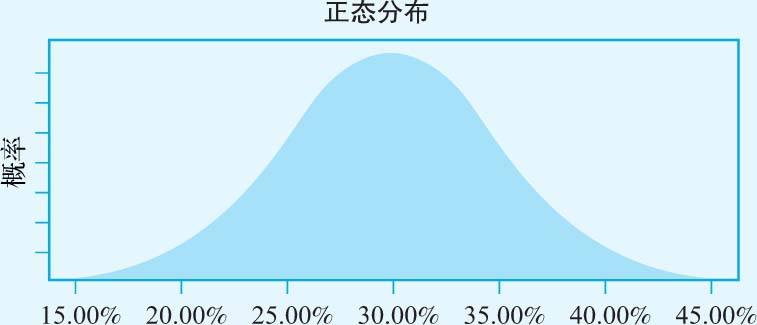
图3-11 再投资率的分布规律
然而,再投资率极有可能是资本收益率的函数,如果资本收益率很高,那么再投资率也会很高。为此,我们假设两者之间的相关系数为0.40,也体现资本收益率与再投资率之间的这种联动。这就形成了如图3-12所示的散点图。
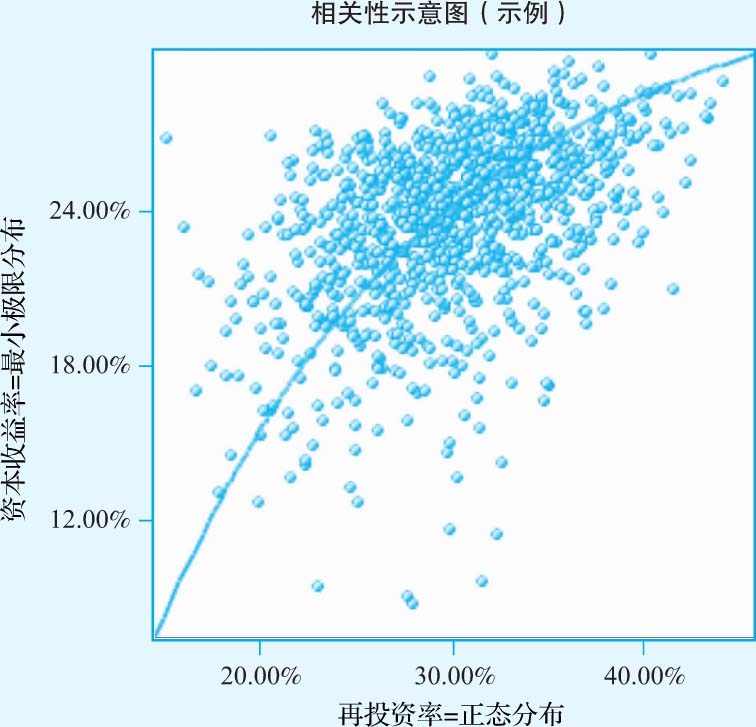
图3-12 资本收益率和再投资率的同步变化
因此,如果资本收益率接近30%,再投资率约为40%。如果资本收益下降到12%,再投资率则下降到20%。
· 贝塔系数 :在基本情境下的估值中,我们根据3M公司所从事的业务,预计其贝塔系数为1.36。我们将贝塔系数用于高增长时期,但这个贝塔系数的估计可能是不正确的。为反映不正确的可能性,我们假设贝塔系数正态分布的预期值为1.36,标准误差为0.07,如图3-13所示。
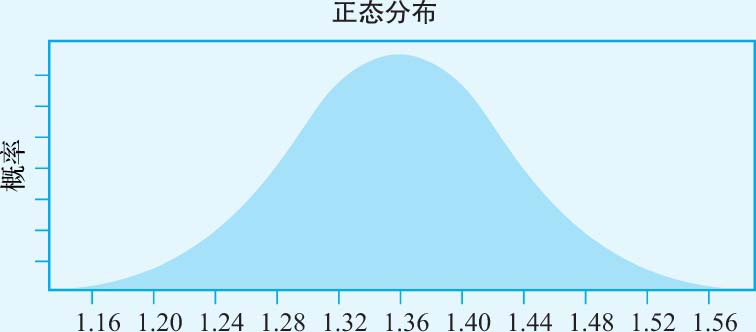
图3-13 贝塔系数的分布
有了这些输入参数,我们就可以对上述指定的参数进行模拟,从而估算3M公司的每股价值,图3-14显示了对我们所得到的分布进行模拟的结果(合计进行了10 000次模拟)。
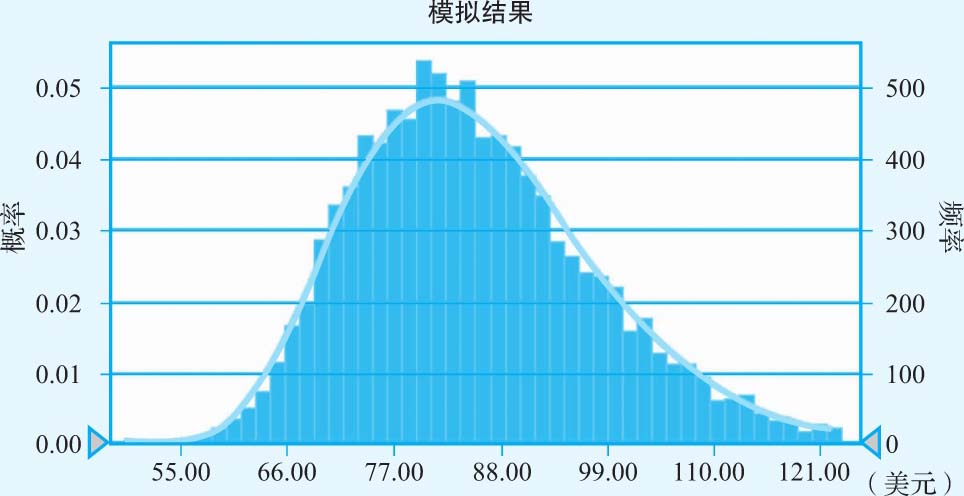
图3-14 针对3M公司每股股票价值的模拟结果
以下是在全部10 000次模拟测试中针对估值得到的关键统计变量:
·在全部模拟中,每股价值的平均值为87.35美元,略高于风险调整后的每股价值86.95美元。中位数为每股87.10美元。
·估值结果存在很大差异。在全部模拟中,最低值是每股55.22美元,最高值是每股121美元。每股价值的标准差为16.15美元。
设计完备的模拟技术不仅仅可以为我们提供资产或业务的预期价值:
· 对输入变量做出更合理的估计 :在理想的模拟模型中,分析人员在确定使用何种分布以及相应的分布参数之前,首先需要检验各输入变量的历史数据和横截面数据。通过这个过程,他们可以避免因点数估计带来的问题。很多折现现金流估值采用的预期增长率,来自Zack或IBES等金融数据库根据分析师一致估计得到的结果。
· 它生成的是预期值的分布,而不是点估计值 :不妨考虑一下我们在案例中除得到每股87.35美元的预期价值之外,我们还估计出这个结果的标准差为16.15美元,并将这个结果按百分位数进行分解。分布函数进一步验证了一个专业但显而易见的结论:估值模型可以对不精确的风险资产得到一个估计值。这也可以解释,不同的分析师为什么会对同一资产得出不同的估值结果。
请注意,对于模拟估值法支持者的常见做法,我们有必要澄清如下两个方面。第一,模拟法取得的预期值确实要好于传统风险调整值模型的结论。事实上,模拟法的期望值应非常接近我们针对每个参数进行点估计(而不是整个分布区间)得到的预期值。第二,通过给出预期价值的估计值及该估计值的分布函数,使得模拟法可以为投资决策提供更好的依据,但这可能不会一贯如此。尽管决策者可以借此更全面地了解风险资产价值的不确定性,但如果滥用这些风险指标,则会让他们的收获大打折扣。正如我们将在本章后面讨论的那样,在模拟法中,重复计算风险以及根据错误类型的风险进行决策,都是常见现象。
要把模拟法用作估值工具,首先我们就必须引入一个约束条件,一旦违背这个约束条件,就有可能给公司带来巨大的成本,甚至会导致公司难以为继。然后我们再检验违背约束条件的概率并与估值成本进行比较,从而考量风险对冲工具的有效性。