




在现值调整中,我们按三个步骤来估计公司的价值。首先,我们考虑的是无杠杆公司的价值。然后,我们再考虑借入一定数量资金带来的税收优惠的现值。最后,评估相应借款金额对企业破产概率及破产预期成本的影响。
这种方法的第一步就是估计无杠杆公司的价值。实际上,我们可以假设在公司没有债务的情况下对公司进行估值——使用无杠杆股权成本对预期的公司自由现金流进行折现。在现金流永续增长的特殊情况下,公司价值很容易取得:
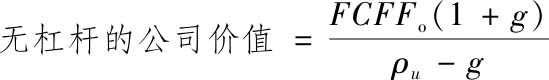
其中,FCFF o 是公司的当期税后经营现金流,ρ u 为股权的无杠杆成本,g为预期增长率。在更为常见的情况下,可以采用任何我们认为合理的增长假设对公司进行估值。估值所需要的参数包括预期现金流、增长率和无杠杆的股权成本。
第二步是计算既定债务水平带来的预期税收收益。这种税收优惠是公司税率的函数,并通过折现反映该现金流的风险:
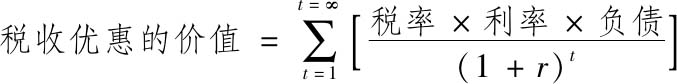
在这里,我们必须解决3个估计问题。首先是用于计算税收优惠的税率,以及该税率是否会随时间而改变。其次是用于计算税收优惠的债务绝对额,以及这个数额是否会随时间而变化。最后就是使用哪个折扣率来计算税收优惠的现值。在现值调整法的初步迭代中,税率和债务绝对额被视为常数(因而税收优惠为永续使用),并以债务的税前成本作为折现率,这就大大简化了税收优惠价值的计算:

随着这种方法不断改进,允许税率和债务绝对额可变,但以债务成本作为折现率是否合理的问题也逐渐浮出水面。费尔南德斯(Fernandez,2004)认为,税收收益的价值应该是如下两个价值之间的差额,即负债企业在享受税收优惠情况下的价值与同一公司在无杠杆情况下的价值之差。因此,他得到的税收优惠价值远远高于按传统方法得到的结果,两者的比例大于无杠杆企业股权成本与债务成本之比。但库珀和尼博格(Cooper and Nyborg,2006)并不认同费尔南德斯的观点,他们认为,债务税盾的价值是利息节约额按债务成本折现后的现值。
第三步是评估既定债务水平对公司违约风险和预期破产成本的影响。至少在理论上,它需要估计附加债务的违约概率以及破产带来的直接成本和间接成本。如果π a 是取得附加债务后的违约概率,而BC为破产成本的现值,那么预期破产成本的现值可以按如下公式进行估算:
预期破产成本的现值=破产概率×破产成本的现值=π a ×BC
在调整现值法的这个步骤中,我们的估计会遇到一个非常严峻的问题,因为破产概率和破产成本是不可能直接估计的。我们可以通过两种基本方法对破产概率做出间接估计。第一种方法和我们在资本成本法中的处理方式一样——估计各级别债券的信用评级,然后按各评级违约概率的经验值作为该级别债券的违约概率。第二种方法是借助统计方法,根据公司可观察到的特征,估计各信用等级债务的违约概率。此外,还可以根据针对实际破产案例成本的实证研究来估计破产成本,但这种方法存在相当大的误差。针对破产直接成本的研究表明,和公司价值相比,这项成本非常小。
 事实上,财务危机的代价远不止传统意义上的破产和清算成本。当公司出现破产征兆时,员工、客户、供应商和贷款人自然做出相应的反应,他们的行为可能会给公司运营造成深层次的严重损害。当企业被认为存在破产风险时,它们会失去原有的客户(和销售额),员工流失加剧,而且和正常企业相比,它们不得不接受供应商更苛刻的供货条款。对于很多公司来说,这些间接破产成本可能是灾难性的,往往是让这种认识发酵为现实的罪魁祸首。针对破产成本规模的实证研究表明,这个数字通常为公司价值的10%~25%。
事实上,财务危机的代价远不止传统意义上的破产和清算成本。当公司出现破产征兆时,员工、客户、供应商和贷款人自然做出相应的反应,他们的行为可能会给公司运营造成深层次的严重损害。当企业被认为存在破产风险时,它们会失去原有的客户(和销售额),员工流失加剧,而且和正常企业相比,它们不得不接受供应商更苛刻的供货条款。对于很多公司来说,这些间接破产成本可能是灾难性的,往往是让这种认识发酵为现实的罪魁祸首。针对破产成本规模的实证研究表明,这个数字通常为公司价值的10%~25%。
