




按风险对折现率进行调整,或是以确定性等价取代不确定的预期现金流,都是我们在调整风险时可采取的方法,但它们是否会带来不同的价值呢?如果是这样的话,哪种方法的结果更精确呢?答案取决于我们是如何计算确定性等价现金流的。如果我们使用风险-收益模型的风险溢价来计算确定性等价值,那么两种方法获得的结果应该是相同的。毕竟,使用确定性等价来调整现金流,然后按无风险利率对现金流进行折现,最终结果就是按风险调整折现率折现的现金流。要理解这一点,不妨考虑一笔1年期单一现金流的资产。假设r是经风险调整后的现金流,r f 为无风险利率,RP是复合风险溢价,那么,按本节前述的公式,我们可以得到:
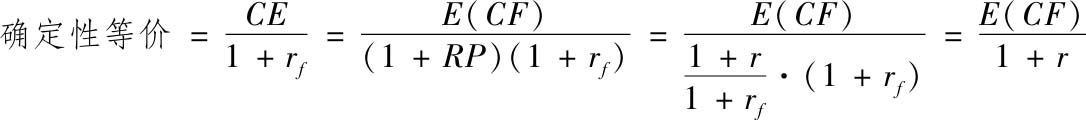
把这个分析拓展到多个时间段,结论仍然是成立的。
 但是需要提醒的是,如果使用的是风险溢价近似值,即风险调整后的收益率和无风险收益率之间的差值,那么这种等价关系将不再成立。在这种情况下,按照确定性等价法,所有风险资产都会拥有较低的价值,并且差异会随着风险溢价的增加而扩大。
但是需要提醒的是,如果使用的是风险溢价近似值,即风险调整后的收益率和无风险收益率之间的差值,那么这种等价关系将不再成立。在这种情况下,按照确定性等价法,所有风险资产都会拥有较低的价值,并且差异会随着风险溢价的增加而扩大。
在其他情况下,两种方法也会对相同风险资产给出不同的价值。一种情况是,无风险利率和风险溢价在不同时间段各不相同,各期间的风险调整折现率同样保持变化。有人认为,在这种情况下,确定性等价法会给出更精确的估值。另一种情况是,确定性等价是按照效用函数或主观计算得出的,而风险调整折现率则来自风险-收益模型。这两种方法会对风险资产带来不同的估值。最后,这两种方法对负现金流的处理方式不同。风险调整折现率以较高折现率对负现金流进行折现,而且随着风险的增加,现值负数的绝对值会有所减小。如果确定性等价采用效用函数计算得出,那么它也会生成负的等价现金流,但随着风险水平的提高,负数的绝对值会增加,这个结果显然是我们可以凭借直觉猜到的。
但最大的问题出现于分析师混合使用多种方法时,此时,他们往往凭借主观臆断对风险进行部分调整,并同时对折现率按风险进行调整。在这种情况下,很容易对风险进行重复计量,而由此对价值进行的风险调整自然难以解释。
在现值调整(adjusted present value,APV)法中,我们将债务融资价值的影响与对企业资产价值的影响分离开。不同于以折现率体现债务融资影响的传统方法,在现值调整法中,对债务利益和成本预期价值的估计与经营性资产价值的估计是独立的。