




在本节中,我们将要讨论的一个现实问题是:如何最合理地将不确定的预期现金流转换为有保障的确定性等价现金流(certainty equivalent cash flow)。尽管我们不能否认现金流取决于风险规避倾向这个观点,但真正的估算依旧难度很大。
计算确定性等价的第一种(也是最原始的)方法源于个体的效用函数。如果能明确个体财富的效用函数,那么我们就已经有条件将这个人的风险现金流转换为确定性等价现金流。比如说,对一个拥有对数效用函数的个人来说,在参加前面提到的赌博游戏(有90%的概率获得100美元,有10%的机会获得50美元)中,他需要的确定性等价现金流就应该是93.30美元:
赌博游戏的效用=0.90×ln(100)+0.10×ln(50)=4.5359
确定性等价=exp 4.535 9 =93.30(美元)
这93.30美元确定性等价带给这个人的效用,等于他参加不确定性赌博游戏取得95美元预期价值的效用。当然,更复杂的资产同样适用于这个原理,我们只需将每个预期现金流转换为确定性等价。
在使用效用模型估计确定性等价的时候,我们可能会看到一个奇怪的现象:正预期现金流的确定性等价可能是负数。我们不妨考虑一项假想的投资:你有50%的概率赚取2000美元,但有50%的概率损失1500美元。这项投资的预期价值应该是250美元(=2000×50%-1500×50%),但确定性等价有可能是负值,最终结果取决于我们所假设的效用函数。

在实践中使用这种方法会带来两个问题。第一个问题是,要精确找到个人或个别分析师的效用函数几乎是不可能的,至少非常困难。事实上,大多数效果良好(体现在数学上)的效用函数似乎无法对实际行为做出合理解释。第二个问题是,即使我们可以指定一个效用函数,但这种方法仍要求我们列示出资产在每个时间段上的所有情景(以及相应的概率)。因此,我们完全可以理解,使用效用函数确定确定性等价的方法,基本还局限于教学中经常提到的简单赌博游戏。
使用风险-收益模型将不确定现金流转换为确定性等价,为我们提供了一种更实用的方法。实际上,我们可以使用相同的方法来估计风险调整折现率时使用的风险溢价,但是在这里,我们可以使用风险溢价来估计确定性等价现金流:

以3M公司的估值为例,请注意,按照市场风险敞口和当前的市场状况,8.63%的资本成本是经过风险调整后的折现率;无风险利率为3.72%。在这里,我们不用8.63%对第一年的预期现金流2698(百万美元)进行折现,相反,我们将这个折现率分解为3.72%的无风险利率和4.73%的复合风险溢价。

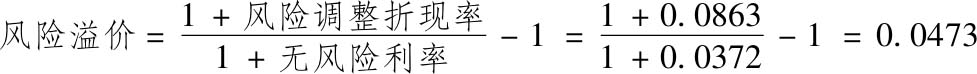
使用这个风险溢价,我们可以计算3M公司在第一年的确定性等价现金流为:
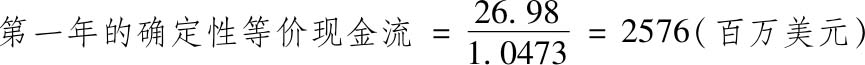
然后,我们再以无风险利率计算该确定性等价现金流的现值:
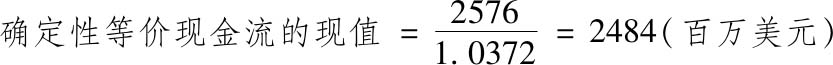
我们可以对所有预期现金流进行上述计算,其中,r代表风险调整后的折现率,r f 代表无风险利率。
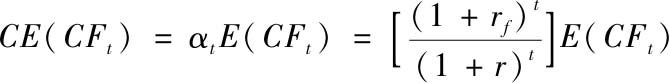
这种调整会带来两种影响。首先,和同一时间点可预测性较高的现金流相比,不确定程度较高的预期现金流会拥有较低的确定性等价值。其次,随着时间的推移,不确定性的影响会持续加大。这就会导致未来不确定现金流的确定性等价低于马上到来的不确定现金流。
为调整现金流的不确定性,一种更为常见的方法就是对不确定的现金流进行主观“折扣”(haircut)。按照这种方法,当分析师面临不确定的现金流时,会以相对保守或打折的估计值代替不确定的现金流。当分析师迫不得已而对不同风险项目使用相同的折扣率,或是想对所有障碍视而不见的时候,这种主观方法就成为他们手中屡试不爽的武器。他们直接对高风险项目的现金流打折,试图以直接减少现金流数量的方法,弥补未通过调整折现率体现出的额外风险。
在现实中,这种方法可以有多种形式,有些投资者只考虑可预测资产带来的现金流;于是,在对资产进行估值时,他们干脆忽略有风险的现金流或投机性现金流。沃伦·巴菲特始终对CAPM和其他风险与收益模型不屑一顾,他主张以无风险利率作为折现率。但我们认为,他之所以这么做,完全是因为他选择投资的公司类型,当然,他在估计现金流方面始终采取的保守态度,这或许也是其中的原因之一。
虽然现金流折扣法表面上似乎很有吸引力,但我们还是应审慎使用这种方法。毕竟,即便是对于同一资产,分析师对风险的直觉也会有着天壤之别;和喜欢冒险的分析师相比,风险规避型分析师会对相同资产的现金流给予更大的折扣。此外,在构建风险收益模型时,我们需要对可分散的企业风险与不可分散的市场风险进行区分,但是当分析师依赖直觉来判断风险时,这种区分会荡然无存。换句话说,对于通过投资组合即可分散抵消的风险,他们依旧会“简单粗暴”地对现金流打折。风险调整过程缺乏透明度,也会导致风险被重复计算,尤其是需由若干分析师进行多层分析时。比如说,研究风险投资的第一位分析师对现金流采取了保守性估计,但是在他将分析结果提交给上级时,后者有可能会对已进行风险调整的现金流再次做风险调整。